Сформулируйте закон инерции первый закон ньютона – Первый закон Ньютона. Формула первого закона Ньютона. Инерциальная система отсчета
- Комментариев к записи Сформулируйте закон инерции первый закон ньютона – Первый закон Ньютона. Формула первого закона Ньютона. Инерциальная система отсчета нет
- Советы абитуриенту
- Первый закон движения Ньютона: Инерция
- I.2.1 ПЕРВЫЙ ЗАКОН НЬЮТОНА. ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЁТА.
- Инерция. Законы Ньютона / «Естествознание»
- 3.1.1. Первый закон Ньютона. Инерциальные системы отсчета
- Инерциальные системы отсчета: первый закон Ньютона
- Первый закон Ньютона: инерция
- Закон инерции | Virtual Laboratory Wiki
Первый закон движения Ньютона: Инерция
 Тело, такое как футбольный мяч, останется в покое, если на него не воздействует внешняя сила.
Тело, такое как футбольный мяч, останется в покое, если на него не воздействует внешняя сила.Первый закон движения Исаака Ньютона описывает поведение массивного тела в покое или в равномерном линейном движении, т. е. Не ускоряется и не вращается. Первый закон гласит: «Тело в состоянии покоя будет оставаться в покое, а тело в движении останется в движении, если на него не воздействует внешняя сила».
Это просто означает, что вещи не могут начинаться, останавливаться или изменять направление самостоятельно. Для этого требуется какая-то сила, действующая на них извне. Хотя эта концепция кажется нам простой и очевидной сегодня, во времена Ньютона она была действительно революционной.
Ньютон опубликовал свои законы движения в 1687 году в своей оригинальной работе «Philosophiæ Naturalis Principia Mathematica» («Математические принципы естественной философии»), в которой он формализовал описание того, как массивные тела движутся под воздействием внешних сил.
Сила трения
Ньютон раскрыл более раннюю работу Галилео Галилея, которая разработала первые точные законы движения для масс, по словам Грега Ботуна, профессора физики в Университете штата Орегон. Эксперименты Галилея показали, что все тела ускоряются с одинаковой скоростью независимо от размера или массы. Ньютон также критиковал и расширил работу Рене Декарта, который также опубликовал набор законов природы в 1644 году, через два года после рождения Ньютона. Законы Декарта очень похожи на первый закон движения Ньютона.
В то время большинство людей считали, что естественное состояние тела должно быть в состоянии покоя. Было очевидно, что придание движению покоящему телу требуется применение внешней силы. Однако считалось, что для поддержания тела требуется постоянная внешняя сила. Основываясь на их опыте с бытовыми объектами, это был не совсем необоснованный вывод. В конце концов, если ваша лошадь перестанет тянуть, ваш фургон перестанет катиться, и если ветер перестанет дуть, ваша лодка перестанет двигаться. Поэтому люди полагали, что эти объекты просто возвращались в свое естественное состояние покоя. Для того, чтобы понять, что должна быть внешняя сила, действующая, чтобы остановить движение этих объектов, потребовался замечательный скачок интуиции.
Возьмите случай плоского камня, скользившего по гладкой поверхности замерзшего озера. Если бы этот камень был куском полированного мрамора, он бы скользнул значительно дальше, чем грубая брусчатка. Очевидно, что сила трения больше на грубой брусчатке, чем на полированном мраморе. Однако, хотя сила трения между мрамором и льдом меньше, чем между шероховатым камнем и льдом, он все еще не равен нулю.
Что произойдет, если сила трения будет сведена к нулю? Мысли Ньютона в этом случае состояли в том, что без присутствия внешней силы, такой как трение, действующее на движущееся тело, для этого не было причин останавливаться.

Инерциальные системы отсчета
Это свойство массивных тел сопротивляться изменениям в их состоянии движения называется инерцией, что приводит к понятию инерциальных систем отсчета. Инерциальную систему отсчета можно описать как трехмерную систему координат, которая не ускоряется и не вращается; однако он может находиться в равномерном линейном движении относительно некоторой другой инерциальной системы отсчета. Ньютон никогда явно не описывал инерциальные системы отсчета, но они являются естественным следствием его Первого Закона Движения.
Когда мы говорим, что тело в движении, можно спросить, в движении по сравнению с чем? Могли бы вы поймать мяч со скоростью 100 миль в час голой рукой? Могли бы, если бы ехали на поезде, идущем на скорости 100 миль в час, и кто-то на этом поезде мягко бросил вам мяч. Поезд и путь существуют в своих собственных инерциальных системах отсчета, а скорость шара зависит от инерциальной системы отсчета, с которой она просматривается. Если бы вы стояли на платформе, и пассажир на этом поезде бросил мяч в окно, вам было бы нецелесообразно пытаться поймать его своей голой рукой.
Первый закон Ньютона в действии
Ракеты, путешествующие через космос, охватывают все три закона движения Ньютона.
Перед запуском ракеты она находится в состоянии покоя на поверхности Земли. Она оставалась бы в состоянии покоя бесконечно без какой-либо внешней силы, действующей на нее. Первый закон Ньютона также применяется, когда ракета скользит по пространству без внешних сил на ней, она будет двигаться по прямой с постоянной скоростью всегда.
Теперь, когда мы знаем, как ведет себя объект, если на него нет внешней силы, что происходит, когда есть внешняя сила, например, двигатель, который запускаются, чтобы запустить ракету в космос? Эта ситуация описана вторым законом движения Ньютона.
tagweb.ru
I.2.1 ПЕРВЫЙ ЗАКОН НЬЮТОНА. ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЁТА.
Первый закон Ньютона: всякое тело сохраняет своё состояние покоя или равномерного прямолинейного движения до тех пор, пока внешнее воздействие не заставит его изменить это состояние.
Первый закон Ньютона утверждает, что состояние покоя или равномерного прямолинейного движения не требует для своего поддержания каких-либо внешних воздействий. В этом проявляется особое динамическое свойство тел, называемое инертностью. Соответственно первый закон Ньютона называют также законом инерции, а движение тела, свободного от внешних воздействий, – движением по инерции.
В приведённой формулировке первого закона Ньютона подразумевается, что тело не деформируется, т.е. абсолютно твёрдое, и что в отсутствие внешних воздействий, оно движется поступательно. Кроме того, твёрдое тело может также ещё и равномерно вращаться по инерции. Если в первом законе Ньютона говорить не о «теле», а о материальной точке, которая по самому её определению не может ни деформироваться, ни вращаться, то необходимость во всех этих оговорках отпадает. Учитывая всё сказанное, можно дать следующую формулировку этого закона:
То, что тело остаётся в покое (т.е. сохраняет скорость, равную нулю) пока на него не действует другое тело, – вполне понятно и подтверждается повседневными наблюдениями. Камень сам не тронется с места, пока не будет кем-нибудь или чем-нибудь сдвинут. Но нам трудно поверить, что тело может вечно сохранять равномерное и прямолинейное движение. Брошенный камень испытывает сопротивление воздуха и притяжение к земле. Если бы этих воздействий не было, тело сохраняло бы состояние равномерного и прямолинейного движения (т.е. сохраняло бы величину и направление своей скорости). Или ещё один пример, разбежавшись, человек не может мгновенно остановиться или мгновенно свернуть в сторону. Чтобы обогнуть на бегу столб, человек инстинктивно хватается за него рукой, т.е. прибегает к воздействию другого тела (столба), чтобы изменить направление своей скорости.
I.2.2 СИЛА
Силой называется векторная физическая величина, являющаяся мерой воздействия на материальную точку или тело со стороны других тел или полей.
Особая форма материи, связывающая частицы вещества в единые системы и передающая с конечной скоростью действия одних частиц на другие называется
Поле, действующее на материальную точку с силой , называется стационарным полем, если оно не изменяется с течением времени , т.е. если в любой точке поля
.
Взаимодействие между удалёнными телами осуществляется посредством гравитационного и электромагнитного полей.
Гравитационное взаимодействие – возникает между телами в соответствии с законом всемирного тяготения.
Электромагнитное взаимодействие – возникает между телами или частицами, обладающими электрическими зарядами.
Кроме того, различают ещё сильное взаимодействие, существующее, например, между частицами, из которых состоят ядра атомов и слабое взаимодействие, характеризующее, например, процессы превращения некоторых элементарных частиц.
В задачах механики учитываются гравитационные силы (силы тяготения) и две разновидности электромагнитных сил – силы упругости и силы трения.
Силы взаимодействия между частями некоторой рассматриваемой системы тел называются внутренними силами.
Силы воздействия на тела данной системы со стороны других тел, не включённых в эту систему, называются внешними силами.
Совокупность физических тел, у которых взаимодействия с внешними телами отсутствуют или скомпенсированы, называется замкнутой (изолированной) системой.
Сила полностью определена, если заданы её модуль, направление и точка приложения. Прямая, вдоль которой направлена сила, называется линией действия силы.
Одновременное действие на материальную точку нескольких сил ( , …, ) эквивалентно действию одной силы, называемой равнодействующей или результирующей силой и равной их геометрической сумме:
Формула (I.48) представляет собой принцип суперпозиции сил.
ВИДЫ СИЛ В ПРИРОДЕ
Наиболее простыми видами сил являются такие, которые обусловлены непосредственным механическим действием одного тела на другое при их соприкосновении, к ним относятся: силы тяги, трения, давления, упругости, натяжения.
Остановимся лишь на некоторых из них.
Силы упругости.Силы, возникающие при упругой деформации тел, называются силами упругости. Эти силы действуют между соприкасающимися слоями деформируемого тела, а также в месте контакта деформируемого тела с телом, вызывающим деформацию.
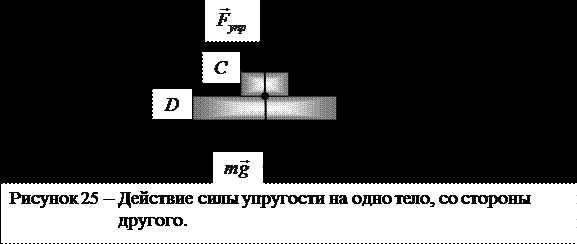
Например, со стороны упруго деформированной доски на брусок , лежащий на ней (рис. 25), действует сила упругости . Силы упругости являются силами электромагнитной природы.
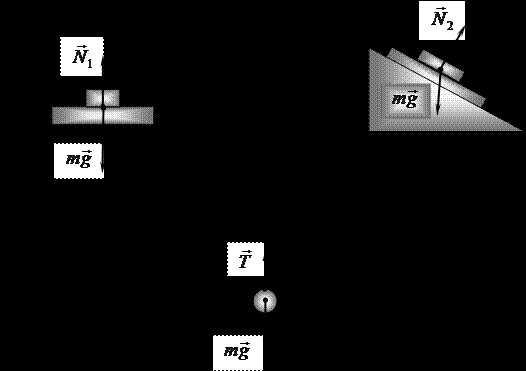
Сила упругости, действующая на рассматриваемое в данной задаче тело со стороны опоры или подвеса, называется силой реакции опоры (подвеса) или силой натяжения подвеса. На рис. 26 приведены примеры приложения к телам сил реакции опоры (силы ) и силы натяжения подвеса (сила ).
 |
|
Сила упругости зависит только от изменения расстояний между взаимодействующими частями данного упругого тела. Работа силы упругости не зависит от формы траектории и при перемещении по замкнутой траектории равна нулю. Поэтому силы упругости являются потенциальными силами (
Закон Гука:сила упругости пропорциональна вектору удлинения (сжатия) и противоположна ему по направлению:
, (I.49)
где – жёсткость тела – величина, определяемая силой упругости, возникающей при единичной деформации данного тела;
– вектор удлинения – величина, характеризующая одномерное (линейное) растяжение (сжатие).
Силы трения.При всяком перемещении одного тела по поверхности другого возникает сопротивление этому движению, которое мы представляем себе как силу трения, направленную против этого движения.
Различают внешнее и внутреннее трение. Внешним трением называется механическое сопротивление, возникающее при относительном перемещении двух соприкасающихся тел в плоскости их касания. Например, внешнее трение существует между бруском и наклонной плоскостью, на которой лежит брусок или с которой он соскальзывает. При определённых условиях внешнее трение переходит во внутреннее трение, при котором в зоне контакта нет скачка скорости при переходе от одного тела к другому.
Трение между поверхностями двух соприкасающихся твёрдых тел при отсутствии между ними жидкой или газообразной прослойки называется сухим трением. Трение между поверхностью твёрдого тела и окружающей его жидкой или газообразной средой, в которой тело движется, называется жидким или вязким трением.
Сухое трение подразделяют на:
§ трение покоя – трение при отсутствии относительного перемещения соприкасающихся тел;
§ трение скольжения – трение при относительном движении соприкасающихся тел.
Сила трения, препятствующая возникновению движения одного тела по поверхности другого, называется
Обычно, говоря о силе трения покоя, имеют в виду предельную силу трения покоя . Обозначим через внешнюю силу, прикладываемую к телу, находящемуся в соприкосновении с другим телом. Эта сила параллельна плоскости соприкосновения. Относительное движение тела возникает при условии . Сила трения покоя вызывается зацеплением неровностей поверхностей тел, упругими деформациями этих неровностей и сцеплением (слипанием) тел в тех местах, где расстояния между их частицами оказываются малыми и достаточными для возникновения межмолекулярного притяжения. В связи с этим силу трения покоя можно рассматривать как разновидность проявления сил упругости.
Опытным путём установлено, что максимальная сила трения покоя ( ) не зависит от площади соприкосновения тел и приблизительно пропорциональна модулю силы нормального давления ( ), прижимающей трущиеся поверхности друг к другу: .
Безразмерный множитель называется коэффициентом трения покоя. Он зависит от природы и состояния трущихся поверхностей.
Трение скольжения объясняется шероховатостью трущихся поверхностей. Большую роль играют также силы межмолекулярного взаимодействия.
Законы трения скольжения.
I. Отношение силы трения к силе давления (т.е. к силе, которая прижимает друг к другу трущиеся поверхности) есть величина для данных поверхностей постоянная.Первый закон трения можно сформулировать и так: сила трения прямо пропорциональна силе давления.Экспериментально показано, что сила трения скольжения пропорциональна силе нормального давления: .
II. Коэффициент трения зависит от материалов трущихся поверхностей.
III. Коэффициент трения не зависит от величины трущихся поверхностей
IV. Коэффициент трения уменьшается с увеличением скорости движения.Это объясняется тем, что при больших скоростях не все выступы шероховатых поверхностей успевают достаточно глубоко зацепиться друг за друга.
На рисунке 27 приведён график зависимости коэффициента трения от скорости движения .
 |
Из графика видно, что наибольший коэффициент трения (следовательно, и наибольшая сила трения) существует в состоянии покоя. Это кратко выражают так: максимальное значение силы трения покоя больше силы трения скольжения. Законы I, II и III были найдены Кулоном из опытов с трибометром.
Примечание: в простейших случаях сила трения и сила нормального давления связаны неравенством , обращающимся в равенство только при наличии относительного движения. Это соотношение называется законом Амонтона – Кулона (эмпирический закон, устанавливающий связь между силой трения, возникающей при скольжении тела по поверхности, с силой нормального давления, действующей на тело со стороны поверхности). Для большинства пар материалов значение коэффициента трения не превышает 1 и находится в диапазоне от до . Если коэффициент трения превышает 1 ( ), это означает, что между контактирующими телами имеется сила адгезии и формула расчёта коэффициента трения меняется на .
Адгезия зависит от природы контактирующих тел, свойств их поверхностей и площади контакта. Адгезия определяется силами межмолекулярного притяжения
Похожие статьи:
poznayka.org
| ||||||||||||||||||||||||||||||||
Рис. 1 Преобразование Галилея | ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
Рис. 2 Галилео Галилей (1564–1642) и Исаак Ньютон (1642–1727) | ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
Рис. 3 Нахождение вектора равнодействующей силы | ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
Рис. 5 Иллюстрация третьего закона Ньютона | ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||
nscience.ru
3.1.1. Первый закон Ньютона. Инерциальные системы отсчета
В качестве первого закона Ньютон взял принцип инерции Галилея (1632 год) и дополнил его понятием инерциальной системы отсчета. Согласно принципу инерции Галилея свободное тело сохраняет состояние, покоя или равномерного, прямолинейного движения пока воздействие других тел не выведет его из этого состояния.
Из этого принципа следует, что состояние покоя или равномерного прямолинейного движения не требует для своего поддержания каких-либо внешних воздействий. В этом проявляется особое динамическое свойство тел, называемое инерцией. Поэтому первый закон Ньютона называют законом инерции, а движение тела в отсутствие воздействий со стороны других тел – движением по инерции.
Первый закон Ньютона выполняется не во всех системах отсчета. Те системы, в которых он выполняется, называются инерциальными системами отсчета.
Экспериментально установлено, что практически инерциальной системой отсчета является гелиоцентрическая система отсчета, начало координат которой находится в центре Солнца, а оси проведены в направлении трех удаленных звезд, выбранных, например, так, чтобы они были взаимно перпендикулярны.
Для многих практических целей при движении макроскопических тел в качестве системы отсчета используется система, связанная с Землей. Такая система отсчета считается приближенно инерциальной из-за влияния суточного и годового вращения Земли.
Таким образом, можно дать следующую формулировку первого закона Ньютона: существуют такие системы отсчета, в которых тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие других тел не выведет его из этого состояния.
Покажем,
что любая система отсчета, которая
движется равномерно и прямолинейно
относительно инерциальной системы,
также является инерциальной. Пусть тело
А покоится в инерциальной системе
отсчета К (рис. 3.1). Система отсчета К’
движется относительно системы К
равномерно и прямолинейно со скоростью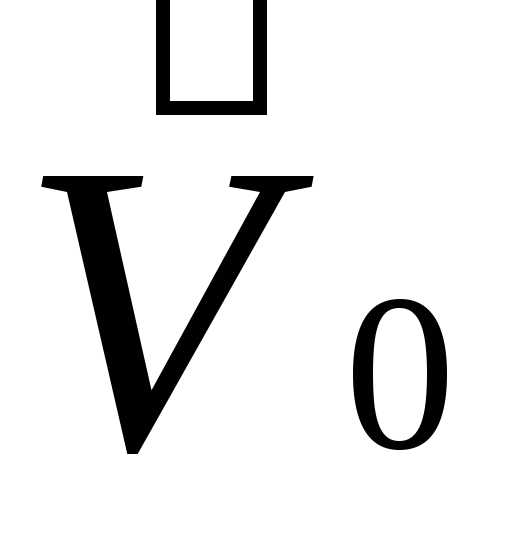 .
Тело А относительно системы К’
движется равномерно и прямолинейно со
скоростью –
.
Тело А относительно системы К’
движется равномерно и прямолинейно со
скоростью –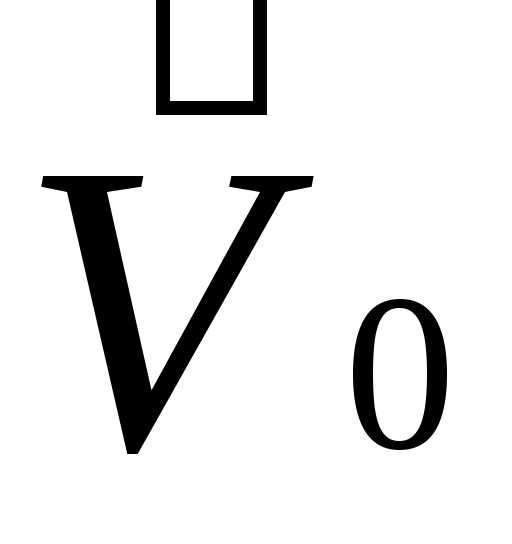 ,
что также удовлетворяет первому закону
Ньютона. Следовательно, система отсчета
К’ является инерциальной. Таким образом,
по известной одной инерциальной системе
отсчета можно описанным выше способом
построить их сколько угодно.
,
что также удовлетворяет первому закону
Ньютона. Следовательно, система отсчета
К’ является инерциальной. Таким образом,
по известной одной инерциальной системе
отсчета можно описанным выше способом
построить их сколько угодно.
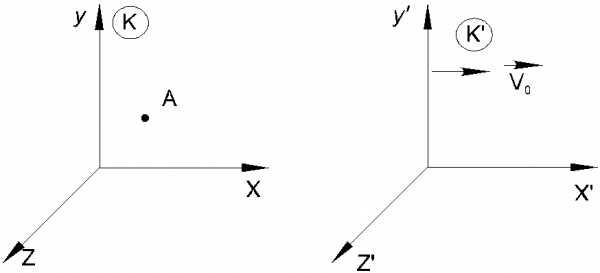
Рис 3.1
3.1.2. Второй закон Ньютона
Этот закон является основным законом динамики материальной точки и твердого тела, движущегося поступательно.
Закон устанавливает связь между силой, массой и ускорением.
Опыт показывает, что всякое изменение величины или направления скорости движения тела вызывается его взаимодействием с другими телами.
В механике сила определятся как количественная мера взаимодействия тел, которое приводит к изменению их скорости или деформации.
Сила характеризуется величиной, направлением и точкой приложения. Следовательно, сила является векторной величиной.
По современным представлениям, основанным на опыте, все наблюдаемые в природе взаимодействия могут быть сведены к четырем фундаментальным: гравитационному, слабому, электромагнитному и сильному.
Гравитационное взаимодействие присуще всем материальным объектам. Оно определяется наличием у материальных тел массы и подчиняется закону всемирного тяготения Ньютона. Радиус действия гравитационного взаимодействия неограничен. В области микромира роль гравитационного взаимодействия ничтожно мала.
Слабое взаимодействие – короткодействующее, существует в микромире и проявляется в том, что приводит к определенному виду нестабильности элементарных частиц.
Электромагнитное взаимодействие проявляется при взаимодействии токов и зарядов. Радиус действия электромагнитного взаимодействия неограничен. Оно является определяющим в образовании атомов, молекул и макроскопических тел.
Ядерное или сильное взаимодействие является самым интенсивным. Радиус сильного взаимодействия очень мал ~10-15 м. Благодаря этому взаимодействию протоны и нейтроны удерживаются в ядрах, несмотря на сильное отталкивание протонов.
К нефундаментальным силам относятся силы упругости, трения, сопротивления и другие. Все эти силы могут быть сведены к электромагнитным или гравитационным, однако, это приводит к существенному усложнению решения задач механики. По этой причине в механике силы упругости и трения рассматривают наряду с фундаментальными.
Опытным
путем установлено еще одно важное
свойство сил, проявляющееся при
механическом взаимодействии. Силы в
механике подчиняются принципу
суперпозиции,
который заключается в следующем: одновременное
взаимодействие частицы М с несколькими
другими n частицами
с силами 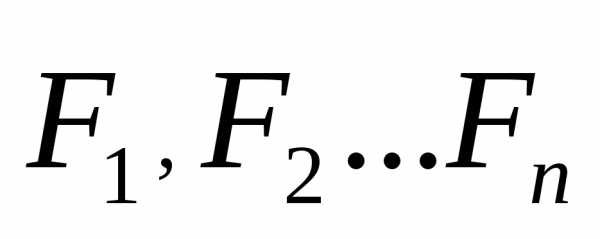 эквивалентно действию одной силы
эквивалентно действию одной силы ,
равной их векторной сумме.
,
равной их векторной сумме.
. (3.1)
Силу  называют равнодействующей.
называют равнодействующей.
Как показывает опыт, все тела обладают свойством препятствовать изменению величины и направления скорости. Это свойство называется инертностью.
Массу можно определить двумя способами. Первый из них состоит в следующем. Выбирается эталонное тело, масса которого mэт принимается за единицу массы. Масса m исследуемого тела определяется из следующего соотношения, установленного опытным путем:
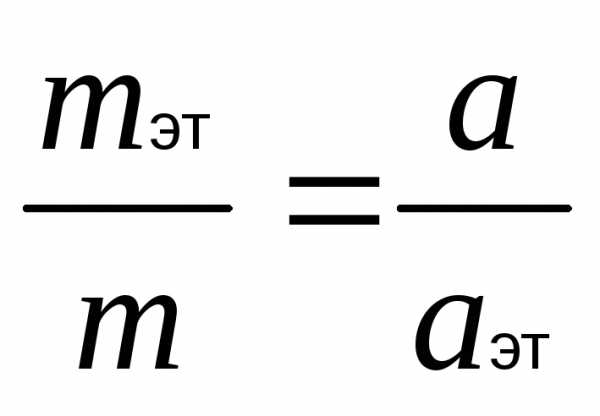 ,
,
где а и аэт – ускорения, вызываемые действием одной и той же силы на эталонное и исследуемое тела. При этом определяется так называемая инертная масса.
Второй способ основан на использовании закона всемирного тяготения. При этом определяется так называемая гравитационная масса.
А. Эйнштейн сформулировал принцип эквивалентности гравитационной и инертной массы: инертная и гравитационная массы одного и того же тела одинаковы.
Эквивалентность инертной и гравитационной масс позволяет выбрать для них одну единицу измерения. В качестве единицы массы в системе СИ принят килограмм (кг) – масса эталонного платиново-иридиевого тела, хранящегося во Франции в международном бюро мер и весов.
Динамическое
воздействие движущегося тела на другие
тела зависит от скорости и массы. Поэтому
в качестве динамической характеристики
интенсивности движения вводится векторная величина 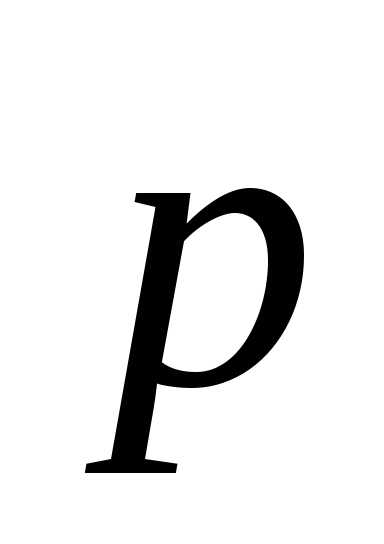 ,
называемая импульсом (или количеством
движения) тела и равная произведению
его массы на скорость:
,
называемая импульсом (или количеством
движения) тела и равная произведению
его массы на скорость:
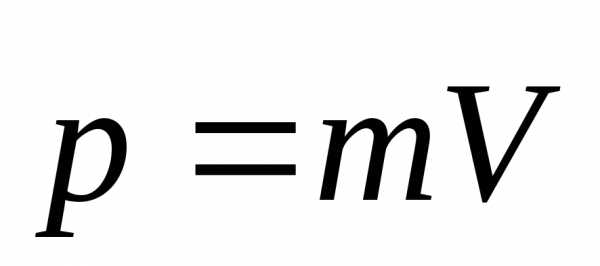 .
(3.2)
.
(3.2)
Единица импульса килограмм-метр, деленный на секунду (кг·м/с).
Согласно второму закону Ньютона, производная по времени от импульса тела равна равнодействующей всех приложенных к нему сил:
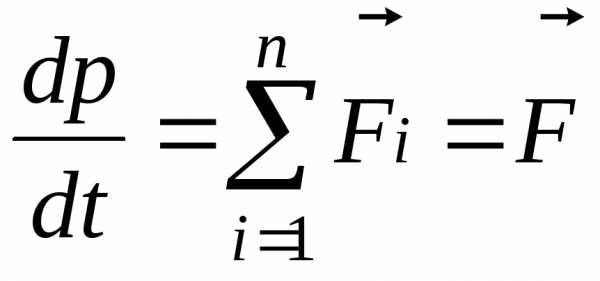 . (3.3)
. (3.3)
Из
(3.3) следует, что изменение
импульса происходит в направлении
равнодействующей силы  . Отметим, что второй закон Ньютона в
форме (3.3) допускает описание движения
тела с переменной массой. Если масса
тела постоянна, то из (3.2) и (3.3) получаем
уравнение второго закона Ньютона в виде
. Отметим, что второй закон Ньютона в
форме (3.3) допускает описание движения
тела с переменной массой. Если масса
тела постоянна, то из (3.2) и (3.3) получаем
уравнение второго закона Ньютона в виде
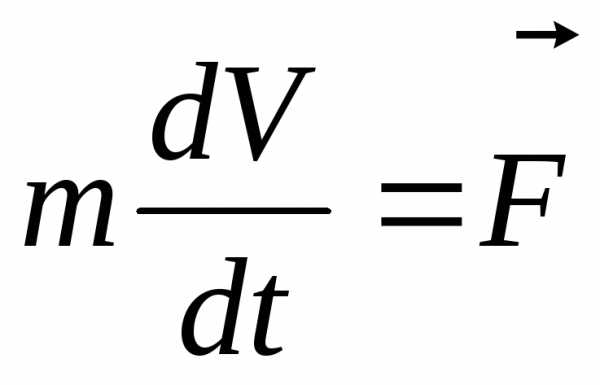 , (3.4)
, (3.4)
откуда с учетом формулы (2.21) получаем:
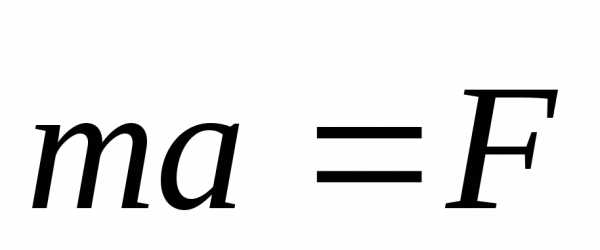 . (3.5)
. (3.5)
Единица силы в СИ является производной единицей, определение которой основано на формуле (3.5). Единица силы – 1 Ньютон (Н), это такая сила, которая телу с массой 1 кг сообщает ускорение 1м/с2.
Второй закон Ньютона часто называют основным законом динамики поступательного движения. С помощью этого закона в механике решаются две основные задачи:
1. Прямая основная задача – установление дифференциальных уравнений движения тела (точки) и их решение.
2. Обратная основная задача – нахождение зависимости сил взаимодействия тел от их координат, скоростей и времени, то есть установление законов взаимодействия.
studfiles.net
Инерциальные системы отсчета: первый закон Ньютона
С древнейших времен движение материальных тел не переставало волновать умы ученых. Так, например, сам Аристотель считал, что если на тело не действуют никакие силы, то такое тело всегда будет находиться в покое.
И лишь только спустя 2000 лет итальянский ученый Галилео Галилей смог исключить из формулировки Аристотеля слово «всегда». Галилей понял, что пребывание тела в состоянии покоя не является единственным следствием отсутствия внешних сил.
Тогда Галилей заявил: тело, на которое не действуют никакие силы, будет либо находиться в покое, либо двигаться равномерно прямолинейно. То есть, движение с одинаковой скоростью по прямой траектории, с точки зрения физики, равнозначно состоянию покоя.
Что есть состояние покоя?
В жизни этот факт наблюдать очень сложно, поскольку всегда имеет место сила трения, которая не дает предметам и вещам покидать свои места. Но если представить себе бесконечно длинный, абсолютно скользкий и гладкий каток, на котором стоит тело, то станет очевидно, что если придать телу импульс, то тело будет двигаться бесконечно долго и по одной прямой.
И в самом деле, на тело действую только две силы: сила тяжести и сила реакции опоры. Но расположены они на одной прямой и направлены друг против друга. Таким образом, по принципу суперпозиции, мы имеем, что общая сила, действующая на такое тело равна нулю.
Однако это идеальный случай. В жизни сила трения проявляет себя почти во всех случаях. Галилей сделал важное открытие, приравняв состояние покоя и движение с постоянной скоростью по прямой линии. Но этого было недостаточно. Оказалось, что условие это выполняется не во всех случаях.
Ясность в этот вопрос внес Исаак Ньютон, обобщивший исследования Галилея и, таким образом, сформулировавший Первый Закон Ньютона.
Первый закон Ньютона: формулируем сами
Существуют две формулировки первого закона Ньютона современная и формулировка самого Исаака Ньютона. В исходном варианте первый закон Ньютона несколько неточен, а современный вариант в попытках исправить эту неточность оказался очень запутанным и потому неудачным. Ну а так как истина всегда где-то рядом, то попытаемся найти это «рядом» и разобраться, что же представляет собой данный закон.
Современная формулировка звучит следующим образом: «Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго».
Инерциальные системы отсчета
Инерциальными называют системы отсчета, в которых выполняется закон инерции. Закон же инерции заключается в том, что тела сохраняют свою скорость неизменной, если на них не действуют другие тела. Получается очень неудобоваримо, малопонятно и напоминает комичную ситуацию, когда на вопрос: “Где это «тут»?” отвечают: “Это здесь”, а на следующий логичный вопрос: “А где это «здесь»?” отвечают: “Это тут”. Масло масляное. Замкнутый круг.
Формулировка самого Ньютона такова: «Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние».
Однако на практике этот закон выполняется не всегда. Убедиться в этом можно элементарно. Когда человек стоит, не держась за поручни, в движущемся автобусе, и автобус резко тормозит, то человек начинает двигаться вперед относительно автобуса, хотя его не понуждает к этому ни одна видимая сила.
То есть, относительно автобуса первый закон Ньютона в изначальной формулировке не выполняется. Очевидно, что он нуждается в уточнении. Уточнением и является введение инерциальных систем отсчета. То есть, таких систем отсчета, в которых первый закон Ньютона выполняется. Это не совсем понятно, поэтому попробуем перевести все это на человеческий язык.
Инерциальные и неинерциальные системы отсчета
Свойство инерции любого тела таково, что до тех пор, пока тело остается изолированным от других тел, оно будет сохранять свое состояние покоя или равномерного прямолинейного движения. «Изолированным» – это значит никак не связанным, бесконечно удаленным от других тел.
На практике это означает, что если в нашем примере за систему отсчета принять не автобус, а какую-то звезду на окраине Галактики, то первый закон Ньютона будет абсолютно точно выполняться для беспечного пассажира, не держащегося за поручни. При торможении автобуса он будет продолжать свое равномерное движение, пока на него не подействуют другие тела.
Вот такие системы отсчета, которые никак не связаны с рассматриваемым телом, и которые никак не влияют на инертность тела, называются инерциальными. Для таких систем отсчета первый закон Ньютона в его исходной формулировке абсолютно справедлив.
То есть закон можно сформулировать так: в системах отсчета, абсолютно никак не связанных с телом, скорость тела при отсутствии стороннего воздействия остается неизменной. В таком виде первый закон Ньютона легко доступен для понимания.
Проблема заключается в том, что на практике очень сложно рассматривать движение конкретного тела относительно таких систем отсчета. Мы не можем переместиться на бесконечно далекую звезду и оттуда осуществлять какие-либо опыты на Земле.
Поэтому за такую систему отсчета условно часто принимают Землю, хотя она и связана с находящимися на ней телами и влияет на характеристики их движения. Но для многих расчетов такое приближение оказывается достаточным. Поэтому примерами инерциальных систем отсчета можно считать Землю для расположенных на ней тел, Солнечную систему для ее планет и так далее.
Первый закон Ньютона не описывается какой-либо физической формулой, однако с помощью него выводятся другие понятия и определения. По сути, этот закон постулирует инертность тел. И таким образом выходит, что для инерциальных систем отсчета закон инерции и есть первый закон Ньютона.
Еще примеры инерциальных систем и первого закона Ньютона
Так, например, если тележка с шаром будет ехать сначала по ровной поверхности, с постоянной скоростью, а потом заедет на песчаную поверхность, то шар внутри тележки начнет ускоренное движение, хотя никакие силы на него не действуют (на самом деле, действуют, но их сумма равна нулю).
Происходит это от того, что система отсчета (в данном случае, тележка) в момент попадания на песчаную поверхность, становится неинерциальной, то есть перестает двигаться с постоянной скоростью.
Первый Закон Ньютона вносит важное разграничение между инерциальными и неинерциальными системами отсчета. Также важным следствием этого закона является тот факт, что ускорение, в некотором смысле, важнее скорости тела.
Поскольку движение с постоянной скоростью по прямой линии суть нахождение в состоянии покоя. Тогда как движение с ускорением явно свидетельствуют о том, что либо сумма сил, приложенных к телу, не равно нулю, либо сама система отсчета, в которой находится тело, является неинерциальной, то есть движется с ускорением.
Причем ускорение может быть как положительным (тело ускоряется), так и отрицательным (тело замедляется).
Нужна помощь в учебе?
Предыдущая тема: Относительность движения: понятие и примеры
Следующая тема:   Второй закон Ньютона: формула и определение + маленький опыт
Все неприличные комментарии будут удаляться.
www.nado5.ru
Первый закон Ньютона: инерция
Физика > Первый закон Ньютона: инерция
Первый закон Ньютона и инерция. Изучите основы механики Ньютона, момент инерции движения в физике, формулировка и формула первого закона, инерциальная система.
Первый закон движения Ньютона концентрируется на инерции. Тело в состоянии покоя будет оставаться стабильным, а смещающийся объект продолжит движение.
Задача обучения
- Разобраться в Первом законе движения.
Основные пункты
- Три закона физики Ньютона составляют основу механики.
- Первый закон гласит: тело в состоянии покоя останется стабильным, пока на него не повлияет внешняя сила, также и движущееся тело останется в движении, пока не почувствует внешнее воздействие.
- Чистая внешняя сила – сумма всех факторов, влияющих на объект.
- Наличие воздействующих сил не означает присутствие чистой внешней силы. Одинаковые по величине силы, но действующие в противоположных направлениях, могут отменить друг друга.
- Трение – сила между перемещающимся телом и поверхностью. Это внешняя сила, влияющая на замедление.
- Инерция – тенденция тела в движении продолжать двигаться. Зависит от массы, поэтому чем тяжелее тело, тем сложнее изменить направление движения.
Термины
- Инертность – свойство объекта, которое вступает в сопротивление с любой трансформацией текущего положения (эквивалентно массе).
- Равномерное движение – перемещение с неизменной скоростью.
- Трение – сила, сопротивляющаяся относительному движению.
История
Исаак Ньютон интересовался перемещением объектов в различных условиях. В 1687 году он описал три знаменитых закона движения, применимых для характеристики физических объектов и систем. Они составляют основу механики и описывают связь сил, воздействующих на тело, и вызванные этим движения. Три закона гласят:
– Если объект не испытывает никакого силового влияния, то скорость останется стабильной. Если объект пребывает в покое, то скорость равняется нулю.
– Ускорение параллельно и прямо пропорционально чистой силе, влияющей на объект, и находится в направлении чистой силы и обратно пропорционально массе.
– Если первый объект влияет силой на второй, то тот одновременно влияет на первый. То есть их силы одинаковы по величине и противоположны по направлению.
Первый закон движения
Итак, тело пребывает в движении или покое, пока на него не воздействует внешняя сила. То есть, движущееся тело сохранит свою скорость, если на него ничего не влияет. Это именуют равномерным движением.
Примеры
Давайте разберем Первый закон Ньютона в конкретной системе отсчета. Представьте, что вы едете на коньках в инерциальной системе. Если оттолкнетесь от одного борта, то по Первому закону Ньютона должны прибыть ко второму. Но этого не случится. Не забывайте, что движение продолжается, если на него не влияет внешняя сила. В нашем мире этой силой чаще всего выступает трение. В данном случае – трение между коньками и льдом.
А как насчет ремней безопасности? В случае автомобильной аварии, они должны защитить нас. Допустим, машина едет со скоростью 60 миль/ч. Если резко затормозить, то машина ощущает внешнюю силу и замедляется. Но на водителя это не действует, поэтому он продолжит перемещаться на прежней скорости. Ремень создает противовес и тормозит человека.
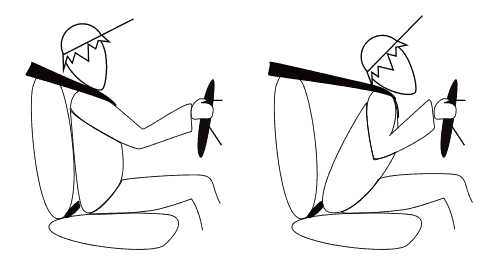
Иллюстрация Первого закона Ньютона
Инертность
Иногда этот закон именуют законом инерции или инерциальной системой отсчета. Она выступает свойством тела фиксироваться в состоянии покоя или смещения (с постоянной скоростью). У некоторых инерция больше, потому что эквивалентна массе. Поэтому сложнее изменить направление валуна, чем шарика для гольфа.
v-kosmose.com
Закон инерции | Virtual Laboratory Wiki
Зако́н ине́рции (Первый закон Нью́тона): свободное тело, на которое не действуют силы со стороны других тел, находится в состоянии покоя или равномерного прямолинейного движения (понятие скорости здесь применяется к центру масс тела в случае непоступательного движения). Иными словами, телам свойственна ине́рция (от лат. inertia — «бездеятельность», «косность»), то есть явление сохранения скорости, если внешние воздействия на них скомпенсированы.
Иными словами: существуют такие системы отсчета, относительно которых тело (материальная точка) при отсутствии на него внешних воздействий (или при их взаимной компенсации) сохраняет состояние покоя или равномерного прямолинейного движения.
Системы отсчёта, в которых выполняется закон инерции, называют инерциальными системами отсчёта (ИСО).
Явлением инерции также является возникновение фиктивных сил инерции в неинерциальных системах отсчета.
Впервые закон инерции был сформулирован Галилео Галилеем, который после множества опытов заключил, что для движения свободного тела с постоянной скоростью не нужно какой-либо внешней причины. До этого общепринятой была иная точка зрения (восходящая к Аристотелю): свободное тело находится в состоянии покоя, а для движения с постоянной скоростью необходимо приложение постоянной силы.
Впоследствии Ньютон сформулировал закон инерции в качестве первого из трёх своих знаменитых законов.
Принцип относительности Галилея: во всех инерциальных системах отсчета все физические процессы протекают одинаково. В системе отсчета, приведенной в состояние покоя или равномерного прямолинейного движения относительно инерциальной системы отсчета (условно — «покоящейся») все процессы протекают точно так же, как и в покоящейся системе.
Следует отметить что понятие инерциальной системы отсчета — абстрактная модель (некий идеальный объект рассматриваемый вместо реального объекта. Примерами абстрактной модели служат абсолютно твердое тело или невесомая нить), реальные системы отсчета всегда связаны с каким-либо объектом и соответствие реально наблюдаемого движения тел в таких системах с результатами расчетов будет неполным.
Ссылки Править
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Закон инерции. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .
ru.vlab.wikia.com



