Скорость материальной точки и ускорение – 3. . —
- Траектория, скорость, ускорение материальной точки — Студопедия.Нет
- 1.Кинематика материальной точки.
- 1.1.4 Ускорение материальной точки
- Кинематика материальной точки 3
- 1 Поступательное движение. Материальная точка. Траектория. Перемещение. Путь. Векторы скорости и ускорения.
- Описание движения материальной точки: радиус-вектор, перемещение, ускорение. Нормальное и тангенциальное ускорение. Законы равноускоренного движения.
- Скорость и ускорение материальной точки в различных СО.
Траектория, скорость, ускорение материальной точки — Студопедия.Нет
Траектория точки. Геометрическое место последовательных положений движущейся точки называется ее траекторией. Если в интервале времени траектория – прямая линия, то движение в этом интервале называется прямолинейным, в противном случае движение называется криволинейным.
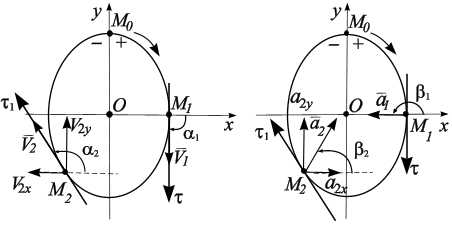
Скорость точки.Пусть положение движущейся точки М относительно произвольно выбранного неподвижного центра О определяется в момент времени t радиус-вектором , который соединяет движущуюся точку М с центром О (рис. 2.1).
За время радиус-вектор изменится на .
Мгновенная скорость точки в момент времени t определяется как предел средней скорости при Dt → 0, т. е.
. (2.1)
Производная по времени от функций обозначается точкой над символом этой функции, а вторая производная – двумя точками.
Вектор скорости приложен в точке
| Скорость– это векторная величина, характеризующая быстроту и направление движения точки |
Ускорение точки.Пусть движущаяся точка М в момент времени t имеет скорость (рис. 2.2). В момент времени = t + Δt эта точка занимает положение , имея скорость . Чтобы изобразить приращение скорости за время Δt, перенесем вектор скорости параллельно самому себе в точку М, тогда .
Ускорением точки в момент времени t называют предел, к которому стремится среднее ускорение при Δt → 0, т. е.
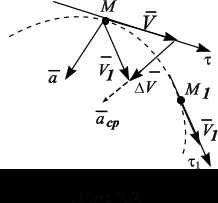
Вектор ускорения всегда направлен внутрь вогнутости под любым углом к касательной к траектории движения (рис. 2.2). Размерность ускорения в СИ: = длина/время2 = м/с2.
| Ускорение – это векторная величина, характеризующая быстроту изменения модуля и направления вектора скорости. |
Движение точки на плоскости
Координатный способ задания движения точки. Зададим радиус-вектор в декартовой системе координат Оху:
.
Тогда движение точки можно задать уравнениями
(2.3)
Уравнения (2.3) являются уравнениями движения точки, а также уравнениями траектории точки, заданными параметрически. Уравнение траектории в системе координат будет иметь вид функции (рис. 2.3). Для получения этой зависимости следует из уравнений (2.3) исключить параметр . Уравнение траектории в явном виде будет иметь вид функции .
Скорость и ускорение точки по модулю и направлению вычисляются по формулам:
Содержание контрольных работ для студентов на тему «кинематика точки» дано в приложении (контрольная работа 1, задача 1).
Пример 2.1. Движение точки M по плоскости Оху задано уравнениями движения
. (а)
Значения х и у – в метрах. Построить траекторию движущейся точки, вычислить скорость и ускорение точки в моменты времени и .
Решение. Дляпостроения траектории движущейся точки в декартовой системе координат определим область, в которой движется точка, т. е. область значений и .[1] Так как и , получаем:
Выделяем область, ограниченную полученными неравенствами, за эту область точка при движении не выходит (рис. 2.4) Исключим параметр t из уравнений движения (a). Для этого делим первое уравнение на 2, второе – на 4, возводим их в квадрат и складываем между собой:
Учитывая, что , получим:
. (б)
Траекторией движущейся точки является эллипс (рис. 2.4). Подставляя в (а) значение , находим:
; м.
Точка в начальный момент времени занимает положение .
Определим направление движения точки. Уравнения движения (а) заданы возрастающей функцией и убывающей функцией , поэтому при увеличении t координата «х» возрастает, а «у» убывает, следовательно, точка движется по эллипсу по часовой стрелке.
| Рис.2.4 | Определим модуль и направление вектора скорости точки М. Имеем:
(в)
Определим модуль и направление вектора ускорения точки |
(г)
При из (а) получаем, что точка М имеет координаты х1= 2,
у1= 0, т. е. занимает положение (рис. 2.4) М1. Подставляя в (в) и (г) время , получим
Откладываем значение скорости (рис. 2.5, а) и ускорения (рис. 2.5, б) точки М1 на траектории.
При из (а) получаем, координаты точки : .
Вычислим, используя (в) и (г), модуль и направление векторов скорости и ускорения.
| |
| а | б |
Рис. 2.5 | |
Имеем:
для ускорения
, .
Откладываем значение скорости (рис. 2.5, а) и ускорения (рис. 2.5, б) точки на траектории.
Вектор скорости точки совпадает по направлению с касательной к траектории в точках и , а вектор ускорения в точках и направлен во внутрь вогнутости траектории (к центру О).
Ответ: V1= 8 м/с, a1= 8 м/с2; V2= 6,3 м/с, a2= 12,6 м/с2.
Естественный способ задания движения точки.
| Рис. 2.6 | При естественном способе задания движения точки задаются (рис. 2.6): – траектория движения точки; – начало и направление увеличения дуговой координаты ; – уравнение движения точки по траектории, как функция времени: где S – дуговая координата, отчитываемая от начала движения. |
Примером естественного способа задания движения является движение поезда: траектория и направление движения определены рельсами, а уравнение движения задано таблицей – расписанием движения поезда.
Движение точки рассматривается в координатах . Единичный вектор направлен по вектору скорости, единичный вектор перпендикулярен вектору , направлен по главной нормали кривой в сторону ее вогнутости (рис. 2.6).
Скорость точки направлена по касательной и равна
Ускорение точки при естественном способе задания движения раскладывается на два – касательное ускорение , и нормальное ускорение :
.
Касательное ускорение характеризует изменение величины скорости, нормальное – изменение направления вектора скорости.
studopedia.net
1.Кинематика материальной точки.
Материальная точка – тело, размерами которого в данной задаче можно пренебречь.Абсолютно твёрдое тело – система материальных точек, расстояние между которыми не изменяется в процессе движения.
Движение тела называется поступательным, если любая прямая, соединяющая две любые его точки, остается всё время параллельной самой себе.
При вращательном движении твёрдого тела все его точки описывают окружности, центры которых лежат на одной прямой – оси вращения.
Радиус-вектор, скорость и ускорение.
Положение точки может быть задано радиус-вектором r, проведённый из начала системы координат к точке. Радиус вектор зависит от времени r=r(t). Векторному уравнению эквивалентна система скалярных уравнений: x=x(t), y=y(t), z=z(t). Называются уравнениями движения материальной точки.
Длина участка траектории АВ пройденного материальной точкой за промежуток t, называется длиной пути s и является скалярной функцией времени. |
На участке АВ вектор средней М скорости равен <V>=r/t и направлен вдоль хорды АВ в ту же сторону, что и вектор перемещения r. Скорость в точке А (мгновенная скорость) V=lim(t0)(r/t)=dr/dt. Вектор мгновенной скорости направлен по касательной к траектории в сторону движения. Так как модуль вектора r равен длине ds малого участка траектории, то =|V|=ds/dt, т.е. модуль скорости равен первой производной по времени.
Быстрота изменения скорости характеризуется вектором ускорения а.
Среднее ускорение – отношение изменения скорости V к промежутку времени t, в течение которого произошло это изменение: <a>=V/t. Вектор среднего ускорения совпадает по направлению с вектором изменения скорости.
Мгновенное ускорение a=lim(t0)(V/t)=dV/dt.
Ускорение – векторная величина, равная первой производной скорости по времени.
Нормальная и тангенциальная составляющая.
Вектор V можно разложить на две составляющие: V – вдоль касательной, Vn – вдоль нормали. V определяет изменение скорости по модулю, Vn – по направлению за промежуток t: a=lim(t0)(V/t)=lim(t0)(V/t)+lim(t0)(Vn/t)=a+an.Модуль тангенциального ускорения равен производной модуля скорости по времени: a=d/dt.
Модуль нормального ускорения: an=2/R, где R – радиус кривизны траектории.
Радиус кривизны
2.Кинематика вращательного движения. Угловые скорость и ускорение.
Пусть радиус окружности, описываемой некоторой точкой, равен r, а её линейное перемещение – ds. Тогда угловое перемещение d (угол поворота радиус-вектора) d=ds/r.
Угловая скорость равна первой производной от угла поворота радиус-вектора по времени: =lim(t0)(/t)=d/dt. Если направление вращения винта совпадает с вращением тела, то конец винта укажет направление вектора .
Время одного полного поворота тела вокруг оси вращения называют периодом обращения T, а величину , обратную периоду, – частотой. =2/T=2.
Единица угловой скорости – рад/с.
Быстрота изменения угловой скорости характеризуется угловым ускорением.
Угловое ускорение равно первой производной от угловой скорости по времени или второй производной от угла поворота радиус-вектора по времени: =lim(t0)(/t)=d/dt=d2/dt2.
Угловое ускорение также является векторной величиной. При ускоренном вращении совпадает с вектором , при замедленном вращении противоположно .
Единица углового ускорения – рад/с2.
studfiles.net
1.1.4 Ускорение материальной точки
Видеоурок 1: Перемещение, скорость, ускорение
Видеоурок 2: Равноускоренное движение – Физика в опытах и экспериментах
Лекция: Ускорение материальной точки
Ускорение
Ускорение – это векторная ФВ, характеризующая быстроту изменения скорости во времени.
Ускорение – это первая производная от скорости, а также вторая – от перемещения.
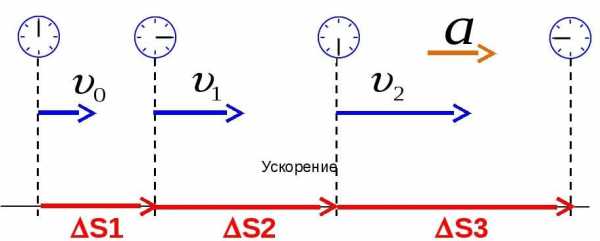
Данная физическая величина показывает, насколько быстро изменяется скорость со временем.
Следует помнить, что ускорением обладает то тело, на которое действует сила.Основной единицей ускорения является 1м/с2.
В отличие от скорости, направление ускорения не всегда совпадает с направлением движения тела. Если тело ускоряется, то ускорение имеет положительное значение, если же тело замедляется, то ускорение – отрицательно. Иными словами, ускорение имеет то же направление, что и результирующая сила, которая действует на тело.
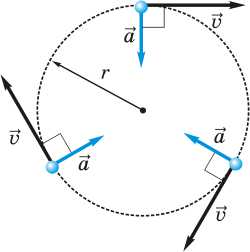
Если тело двигается по окружности, то ускорение направлено к её центру.
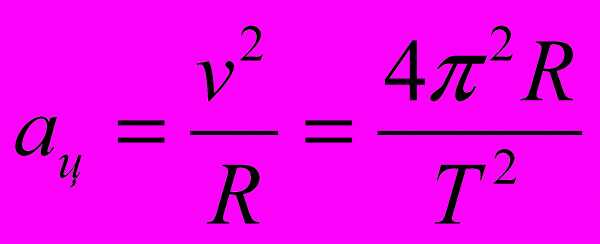
Геометрический смысл ускорения
Геометрическим смыслом ускорения является площадь под прямой графика движения в координатах V(t).
cknow.ru
Кинематика материальной точки 3
Кинематика материальной точки.
1 .Понятие относительности перемещения материальной точки (тела), системы отсчёта .
Движение изменения взаимного расположения тел или матер. Точек.Т.е. мы рассматриваем движение матер точки относительно какого-либо тела или системы тел.
Система отсчёта — это совокупность тела отсчёта, системы координат и часов.
2. Кинематические хар-ки материальной точки.
1)Траектория -линия вдоль которой движется тело.
2)Перемещение -отрезок ,соединяющий начал и конеч положение точки.
3)Скорость -отношение перемещения ко времени для равномер движ.
3 .Путь- это расстояние,пройденное материальной точкой по траектории за промежуток времени и равен длине этой траектории.
4 Ра́диус-ве́ктор — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат . Для произвольной точки в пространстве , радиус -вектор — это вектор, идущий из начала координат в эту точку.Радиус-вектором точки называется вектор, начало которого совпадает с началом системы координат, а конец – с данной точкой.
5 Вектор скорости- это расстояние,которое тело проходит в определённом направлении за единицу времени.Вектор- скорости указывает и скорость и направление движения.
6 Путь – длина отрезка траектории. Траектория – это линия, описываемая материальной точкой при ее движении.
Вычисление пройденного пути
Для равномерного движения
, – весь путь, – весь отрезок времени, – const.Для произвольного движения:
.v1 в течение отрезка Δti приблизительно постоянны, если Δt достаточно мало.
В пределе:
Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора
этой точки:Здесь v — модуль скорости,
— направленный вдоль скорости единичный вектор касательной к траектории в точке .8. Кинематическое уравнение r ( t ) для прямолинейного равномерного движения. Представить в виде проекций на декартовы оси координат.
х=x0+ vx·t.
9. Ускорение материальной точки — векторная физическая величина, характеризующая быстроту изменения скорости и равная приращению скорости за единицу времени. вектор ускорения равен первой производной от вектора скорости по времени или второй производной от радиуса-вектора по времени
10 Тангенциальное ускорение – быстрота изменения скорости по модулю в данный момент времени; производная от скорости по времени.
Нормальное ускорение – быстрота изменения скорости по направлению в данный момент времени.
Полное ускорение определяется векторной суммой тангенциального нормального ускорений.
15.Враща́тельное движе́ние —движение,при котором все точки тела движутся по окружностям,центры которых лежат на одной и той же прямой,называемой осью вращения
18Первый закон Ньютона ..Существуют такие системы отсчёта, относительно которых материальная точка, при отсутствии внешних воздействий, сохраняет состояние покоя или равномерного прямолинейного движения.
Второй закон Ньютона Сила, действующая на тело, равна произведению массы тела на создаваемое этой силой ускорение.
Третий закон Ньютона силы равны по модулю и противоположны по направлению .
20. Виды деформации растяжение-сжатие,сдвиг,изгиб,кручение.
21 Абсолютная деформация – величина изменения размеров тел: длины, объема и т.д.Относительная деформация – отношение величины изменения размера тела к его исходному размеру. Часто относительная деформация выражается в процентах.
22. Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием внешних воздействий. Механическое напряжение в точке тела измеряется отношением силы, возникающей в теле при деформации, к площади малого элемента сечения.
24. Модуль Юнга (модуль упругости, англ. Young modulus, modulus of elasticity) — коэффициент, характеризующий сопротивление материала растяжению/сжатию при упругой деформации. В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал среды и процесса.
25 Закон Гука – связь между величиной упругой деформации и силой, действующей на тело. ввести относительное удлинение ε =∆ l / L и нормальное напряжение в поперечном сечении σ = F / A . В этих обозначениях закон Гука записывается как
=E.Пусть первоначальная длина нерастянутой проволоки составляла L0 . После приложения силы F проволока растянулась и ее длина стала равной L. Величину DL=L-L0 называют абсолютным удлинением проволоки . Величину e=DL/L0 называютотносительным удлинением тела26.Трение скольжения — сила, возникающая при поступательном перемещении одного из контактирующих/взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения;
Трение качения — момент сил, возникающий при качении одного из двух контактирующих/взаимодействующих тел относительно другого
.Трение покоя — сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Она действует в направлении, противоположном направлению возможного движения.
27.Сила трения скольжения всегда направлена против относительной скорости скольжения соприкасающихся тел.
29. СИЛА ТЯЖЕСТИ Силу, с которой тело притягивается к Земле под действием поля тяготения Земли, называют силой тяжести. По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести
31. Вес тела – в физике – сила, с которой тело, действует на опору или на подвес.
32. При́нцип относи́тельности — фундаментальный физический принцип, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.
33. И́мпульс — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v,
34. Изолированная система (замкнутая cистема ) — термодинамическая система , которая не обменивается с окружающей средой ни веществом, ни энергией
35.Центр масс (центр ине́рции , барице́нтр ) в механике — это геометрическая точка, характеризующая движение тела или системы частиц как целого.
36 p=p1 +p2 =const .Формула выражает закон сохранения импульса в замкнутой системе , который формулируют так: полный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел этой системы между собой. Dр=Ft. Группу тел, взаимодействующих не только между собой, но и с телами, не входящими в состав этой группы, называют незамкнутой системой
38 Работа силы – мера механического действия силы при перемещении точки ее приложения.
Кинети́ческая эне́ргия — энергия механической системы , зависящая от скоростей движения её точек.
43.
,т.е. работа силы при деформации тела равна изменению потенциальной энергии этого тела, взятой с обратным знаком.
Величина Еп = т gh называется потенциальной энергией тела, поднятого над Землей
Полной механической энергией системы тел называется сумма кинетической и потенциальной энергий:
mirznanii.com
1 Поступательное движение. Материальная точка. Траектория. Перемещение. Путь. Векторы скорости и ускорения.
Ответы
это механическое движение системы точек (абсолютно твёрдого тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени.
простейшая физическая модель в механике — обладающее массой тело, размерами, формой, вращением и внутренней структурой которого можно пренебречь в условиях исследуемой задачи. Положение материальной точки в пространстве определяется как положение геометрической точки
линия в пространстве, вдоль которой движется тело, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве относительно выбранной системы отсчёта.
изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение.
длина участка траектории материальной точки в физике.
физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени. Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости \vec v тела при его движении за единицу времени:
vec a=d v \ dt
2. Ускорение материальной точки при криволинейном движении. Тангенциальная и нормальная составляющие ускорения.
Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению.Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту). Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости.
Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.
Изменение величины скорости за единицу времени – это тангенциальное ускорение:
3. Вращательное движение. Угловая скорость, угловое ускорение и их связь с линейными скоростями и ускорениями точек вращающегося тела.
Вращ. Движение-вид механического движения. При вращательном движении материальной точки она описывает окружность. При вращательном движении абсолютно твёрдого тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.
Угловая скорость-векторная величина, являющаяся псевдовектором и характеризующая скорость вращения материальной точки вокруг центра вращения. Вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения в единицу времени.
Угловое ускорение-псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости движения материальной точки по окружности.
studfiles.net
Описание движения материальной точки: радиус-вектор, перемещение, ускорение. Нормальное и тангенциальное ускорение. Законы равноускоренного движения.
Механическим движением называют изменение положения тела (или его частей) относительно других тел. Положение тела задается координатой. Иногда размерами тела по сравнению с расстоянием до него можно пренебречь, в этих случаях тело считают материальной точкой. Линию, вдоль которой движется материальная точка, называют траекторией. Длину траектории называют путь.
Принято описывать траекторию материальной точки при помощи радиус-вектора, направление, длина и начальная точка которого зависят от времени.
Скорость – это производная от радиус-вектора материальной точки по времени.
Скорость материальной точки всегда направлена по касательной к дуге, используемой для описания траектории точки. При этом существует связь между величиной скорости v, нормальным ускорением an и радиусом кривизны траектории ρ в данной точке:
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло. Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле
Тангенциальное ускорение, касательное ускорение, составляющая ускорения, направленная по касательной к траектории тела.
Величину тангенциального ускорения — в смысле проекции вектора ускорения на единичный касательный вектор траектории — можно выразить так:
Закон равноускоренного движения
Равноускоренное движение в поле тяжести ЗемлиЗакон равноускоренного движения получается в результате решения простейшего дифференциального уравнения вида:
При этом уравнения движения в координатной форме имеют аналогичный вид:
Общее решение этого уравнения дается формулой:
;
Здесь C1 и C2 — произвольные константы, соответствующие начальной координате и начальной скорости.
Движение с постоянным ускорением называют равноускоренным . Движение с постоянным ускорением подчиняется закону:
;
.
;
.
В этом случае часто говорят о равноускоренном движении, если знаки ax и vx (t) совпадают и о равнозамедленном , если ax и vx (t) имеют противоположные знаки. При этом знак каждой из величин зависит от начального выбора системы отсчета.
Частный случай равноускоренного движения — равномерное движение. В этом случае . Тогда движение описывается закону:
malishev.info
Скорость и ускорение материальной точки в различных СО.
Выберем две системы отчета: неподвижную и движущуюся . Рассмотрим положение точки в обеих системах. В системе точка описывается , а в системе – . Начало системы характеризуется .
, , , .
При этом единичные орты с течением времени не изменяются, а единичные орты . Продифференцируем 1 уравнение:
,
, .
Используя формулы Пуассона:
.
Обозначим :
Формула сложения скоростей примет вид теоремы
– теорема сложения скоростей
– переносная скорость
: скорость тела относительно равна скорости тела относительно и системы отчета относительно . В свою очередь состоит из двух : )
–абсолютная скорость, – относительная скорость.
Теорема сложения скоростей. Абсолютная скорость равна сумме относительной и переносной скоростей.
При и : .
Для нахождения ускорения продифференцируем формулу сложения :
, где
,
– теорема сложения скоростей
, – возникает в случае наличия большой скорости вращения движущейся системы относительно скорости и угла между этими векторами неравному нулю.
может равняться нулю в 3-х случаях:
1– движущаяся система отчета не вращается
2– тело неподвижно относительно
3– угол между и равен нулю
Если движется поступательно и вращательно, то следует теорема Эйлера:
Понятие о силе и массе.
В отличии от кинематики в динамике очень важнейшим является введение новых понятий, которые позволяют сформулировать и изучить причину движения тела. Важнейшим понятием в динамике является понятие силы (F) –характеризующая характер и результат взаимодействия между телами (частями одного тела) . Обычно на тело действует не одна, а несколько сил, в связи с чем необходимо использовать принцип суперпозиции сил, который раскладывается на 3 составляющие:
1) если на тело действует несколько сил, то каждому из них приводят к возникновению своего ускорения, при этом общее ускорение преобразованное = геометрической сумме ускорений вызванных каждой силой в отдельности
2) результирующая сил действующих на тело= геометрической сумме сил приложенных к этому телу
3) если внешние силы компенсируют друг друга, то результирующая внешняя сила=0
Понятие массы:
–инертная , для данного тела отсутствие любой действующей на него силы к приобретенному ускорению есть величина постоянная
–гравитационная масса является величиной аддитивной, т.е. масса всего тела= сумме масс частей этого тела
3) для нахождения инертной массы можно использовать легко измеримую гравитационную массу и соответствующие эталоны. Однако теоретические расчеты и опыты показали что любое тело значение его гравитационной и инертной масс совпадают с точностью до 8-го знака после запятой.
infopedia.su