Уравнение максвелла в дифференциальной форме – 5. Уравнения максвелла. Система уравнений максвелла в интегральной и дифференциальной форме и физический смысл входящих в нее уравнений
- Комментариев к записи Уравнение максвелла в дифференциальной форме – 5. Уравнения максвелла. Система уравнений максвелла в интегральной и дифференциальной форме и физический смысл входящих в нее уравнений нет
- Советы абитуриенту
- Уравнения Максвелла — Википедия
- 39. Уравнения Максвелла в интегральной форме.
- 2. Уравнение Максвелла в дифференциальной форме.
- Уравнения Максвелла в дифференциальной форме
- Уравнения Максвелла в интегральной и дифференциальной форме
- Уравнение Максвелла в интегральной и дифференциальной форме. Их физический смысл, некоторые свойства уравнений Максвелла.
- 2. Уравнение Максвелла в дифференциальной форме.
Уравнения Максвелла — Википедия
Материал из Википедии — свободной энциклопедии
Это стабильная версия, отпатрулированная 24 октября 2018.| Состояние | отпатрулирована |
| Классическая электродинамика |
ru.wikipedia.org
39. Уравнения Максвелла в интегральной форме.
Введение Максвеллом понятия полного тока смещения привело его к завершению созданной им макроскопической теории электромагнитного поля, позволившей с единой точки зрения объяснить электрические и магнитный явления и предсказать новые.
В основе теории Максвелла лежат четыре уравнения, полученные нами ранее:
1. Циркуляция вектора напряженности суммарного поля (циркуляция вектораравна нулю):
(12)
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
2. Обобщенная теорема о циркуляции вектора :
.(13)
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
3. Теорема Гаусса для поля :
(14)
или, если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью ρ:
. (15)
Это уравнение показывает, что в природе существуют электрические заряды.
4. Теорема Гаусса для поля :
. (16)
Это уравнение показывает, что в природе не существуют магнитные заряды.
Дополнительные уравнения, используемые с уравнениями Максвелла. Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует связь:
где – напряженность электрического поля;- магнитная индукция;- электрическое смещение;- напряженность магнитного поля;- плотность тока проводимости; γ – удельная проводимость вещества;и– электрическая и магнитная постоянная; ε и μ – электрическая и магнитная проницаемости.
Совокупность этих 7 уравнений составляют основу электродинамики покоящихся сред.
Уравнения Максвелла для стационарных полей ().
1. ; 2.;
3. ; 4..
Источниками электрического поля являются только электрические заряды, источниками магнитного поля – только токи проводимости. В этом случае электрические и магнитные поля независимы друг от друга, что позволяет изучать отдельно постоянные электрическое и магнитное поля.
40. Уравнения Максвелла в дифференциальной форме
Теоремы векторного анализа, используемые при переходе от интегральной формы уравнения к дифференциальной
1. Теорема Стокса: зная ротор вектора в каждой точке некоторой поверхностиS можно вычислить циркуляцию этого вектора по контуру L, ограничивающему S:
.
.
2. Теорема Гаусса: зная дивергенцию вектора в каждой точке пространства, можно вычислить поток этого вектора через произвольную замкнутую поверхностьS конечных размеров.
.
;
.
Уравнения Максвелла в дифференциальной форме характеризуют поле в каждой точке пространства. Физический смысл уравнений Максвелла в дифференциальной форме тот же, что и уравнения Максвелла в интегральной.
Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла эквивалентны. Однако, если имеются поверхности разрыва (поверхности, на которых свойства среды меняются скачкообразно), то интегральная форма уравнений является более общей.
Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред:
1. ; (на границе раздела нет свободных зарядов)
2. ;
3. ;
4. (на границе раздела нет токов проводимости).
Некоторые следствия из уравнений Максвелла
Уравнения Максвелла – наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в электродинамике такую же роль, как законы Ньютона в механике.
1. Согласно идеям Максвелла, переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным полем, т.е. электрические и магнитные поля неразрывно связаны друг с другом – они образуют единое электромагнитное поле.
2. Теория Максвелла не только смогла объяснить уже известные экспериментальные факты, но и предсказала новые явления: существование магнитного поля токов смещения позволило предсказать существование электромагнитных волн – переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью (скоростью света). Этот вывод и теоретическое исследование свойств электромагнитных волн привели Максвелла к созданию электромагнитной теории света, согласно которой свет представляет собой также электромагнитные волны.
Теория Максвелла была экспериментально подтверждена: электромагнитные волны были получены на практике немецким физиком Герцем, который доказал, что законы их возбуждения и распространения полностью подчиняются уравнениям Максвелла.
3. К электромагнитному полю применим только принцип относительности Эйнштейна, согласно которому, механические, оптические и электромагнитные явления во всех инерциальных системах отсчета протекают одинаково, т.е. описываются одинаковыми уравнениями. Из принципа относительности следует, что раздельное рассмотрение электрического и магнитного полей имеет лишь относительный смысл. Так если электрическое поле создается системой неподвижных зарядов, то эти заряды, являясь неподвижными относительно одной системы отсчета, движутся относительно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. Аналогично, неподвижный проводник с постоянным током, возбуждая в каждой точке пространства постоянное магнитное поле, движется относительно других инерциальных систем, и создаваемое им переменное магнитное поле возбуждает вихревое электрическое поле. Таким образом, поле, которое относительно некоторой системы отсчета оказывается чисто электрическим или чисто магнитным, относительно других систем отсчета будет представлять собой совокупность электрического и магнитного полей.
Вывод: теория Максвелла, ее экспериментальное подтверждение, а также принцип относительности Эйнштейна приводят к единой теории электрических, магнитных и оптических явлений, основанных на представлении об электромагнитном поле
studfiles.net
2. Уравнение Максвелла в дифференциальной форме.
Уравнения (3-6) записаны в интегральной форме. Гораздо чаще используется дифференциальная форма записи этих уравнений, которая позволяет описать электромагнитное поле в любой точке (точнее в любом элементарном объёме) пространства. Уравнения Максвелла в дифференциальной форме легко получаются из уравнений (3-6) путём применения известных из векторного анализа теорем Остроградского-Гаусса и Стокса, устанавливающих связь между линейными, поверхностными и объёмными интегралами:Теорема Остроградского-Гауса связывает объёмный интеграл с поверхностным | , |
где  –
скалярная функция – дивергенция
(расхождение):
–
скалярная функция – дивергенция
(расхождение):
Теорема Стокса связывает поверхностный интеграл с линейным | , |
где  –
векторная функция – ротор (вихрь):
–
векторная функция – ротор (вихрь):
С учётом вышеизложенного уравнения (3-6) принимают вид:
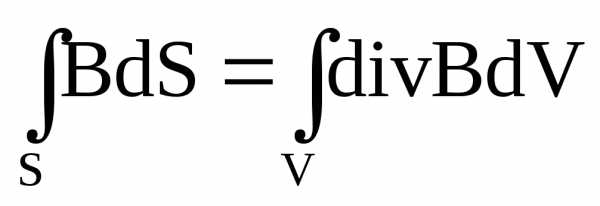
Т.к. объёмы и поверхности, по которым происходит интегрирование произвольны, то можно приравнять подынтегральные функции и получить уравнения Максвелла в дифференциальной форме:
Уравнения Максвелла в дифференциальной форме |
|
3. Материальные уравнения.
Уравнения Максвелла ещё не составляют полной системы уравнений электромагнитного поля. Этих уравнений недостаточно для нахождения полей по заданным распределениям зарядов и токов. Для этого необходимо дополнить соотношения, в которые входили бы величины, характеризующие индивидуальные свойства среды. Для случая изотропных сред (не содержащих сегнетоэлектриков и ферромагнетиков) они имеют следующий вид:
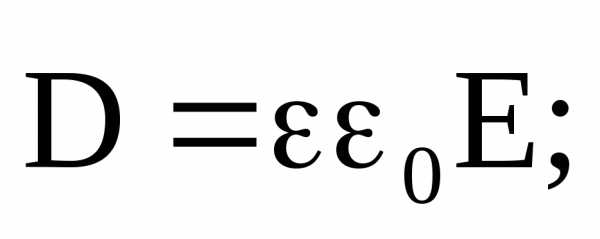
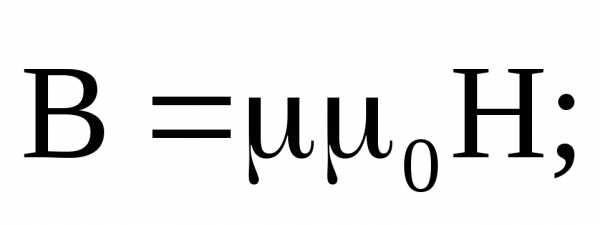
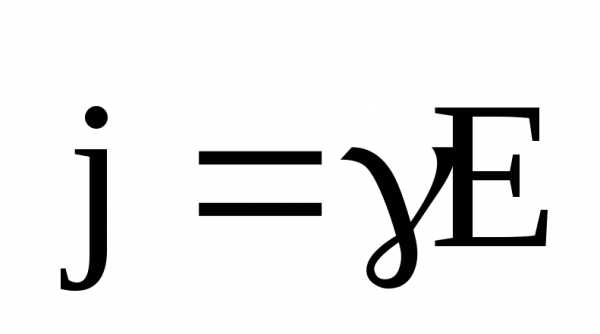 (11)
(11)
С учётом соотношений (11) система уравнений является полной и позволяет описывать все электромагнитные процессы в вакууме и веществе.
4. Свойства уравнений Максвелла.
А. Уравнения Максвелла линейны и
и по времени и пространственным координатам,
а так же первые степени плотности
электрических зарядов ρ и токов γ.
Свойство линейности уравнений
непосредственно связано с принципом
суперпозиции.
по времени и пространственным координатам,
а так же первые степени плотности
электрических зарядов ρ и токов γ.
Свойство линейности уравнений
непосредственно связано с принципом
суперпозиции.
Б. Уравнения Максвелла содержат уравнение непрерывности, выражающее закон сохранения электрического заряда:
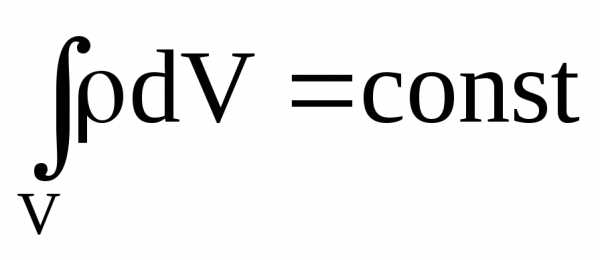
В.Уравнения Максвелла выполняются во всех инерциальных системах отсчёта. Они являются релятивистски-инвариантными, что подтверждается опытными данными.
Г.О симметрииуравнений Максвелла.
Уравнения
не симметричны относительно электрического
и магнитного полей. Это обусловлено
тем, что в природе существуют электрические
заряды, но нет магнитных зарядов. Вместе
с тем в нейтральной однородной среде,
где ρ = 0 и 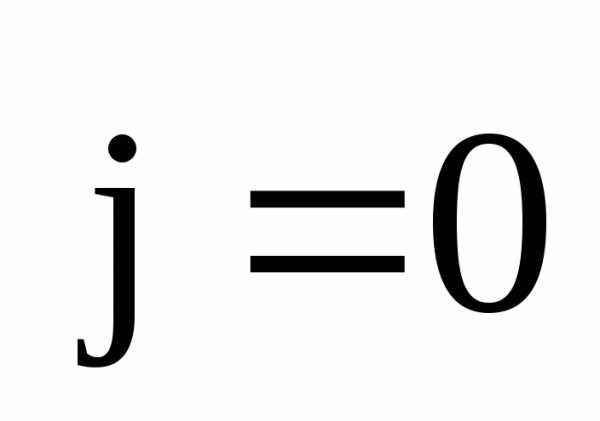 ,уравнения
Максвелла приобретают симметричный
вид, т.е.
,уравнения
Максвелла приобретают симметричный
вид, т.е. так связано с
так связано с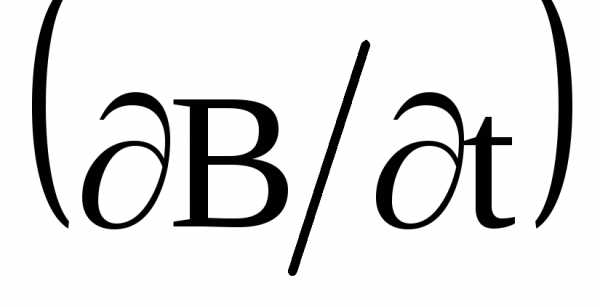 ,
как
,
как с
с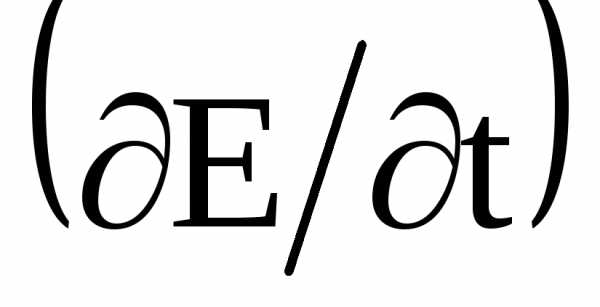 .
.
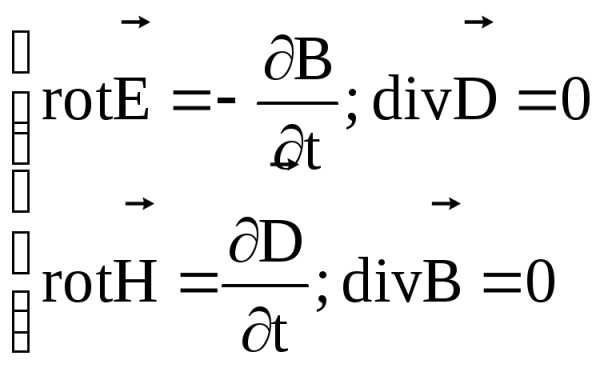
Д. Об электромагнитных волнах.
Из
уравнений Максвелла следует важный
вывод о существовании принципиально
нового физического явления: электромагнитное
поле способно существовать самостоятельно
без электрических зарядов и токов. При
этом изменение его состояния обязательно
имеет волновой характер. Всякое изменение
во времени магнитного поля возбуждает
поле электрическое, изменение
электрического поля, в свою очередь,
возбуждает магнитное поле. За счёт
непрерывного взаимопревращения они и
должны сохранятся. Поля такого рода
называются электромагнитными
волнами. Выяснилось также, что ток
смещения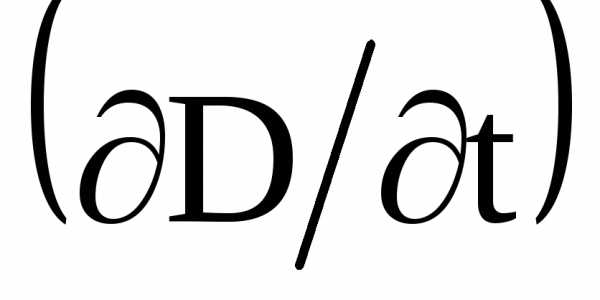 играет в этом явлении первостепенную
роль.
играет в этом явлении первостепенную
роль.
studfiles.net
Уравнения Максвелла в дифференциальной форме
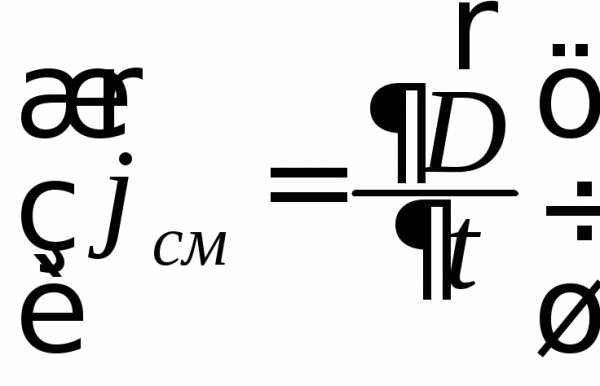 ; (2.5)
; (2.5)
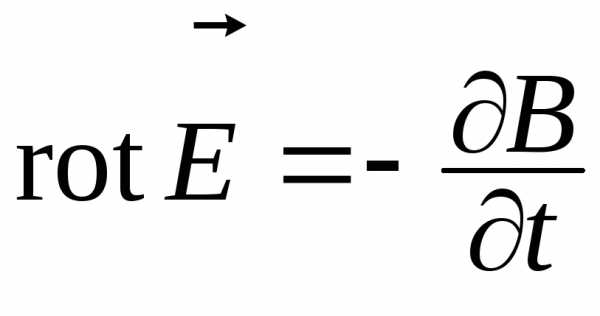 ; (2.6)
; (2.6)
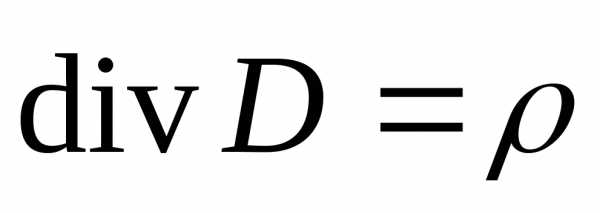 ; (2.7)
; (2.7)
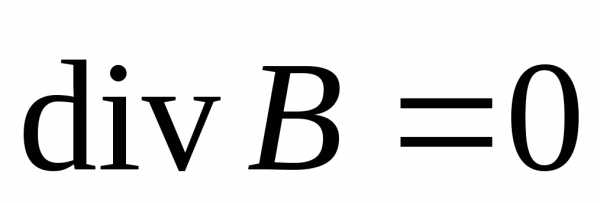 . (2.8)
. (2.8)
Первое уравнение Максвелла в дифференциальной форме (2.5) показывает, что вихревое магнитное поле создается как плотностью тока проводимости, так и тока смещения.
Второе уравнение Максвелла в дифференциальной форме (2.6) показывает, что вихревое электрическое поле создается изменением во времени индукции магнитного поля.
Третье и четвертое уравнения Максвелла в дифференциальной форме отражают наличие носителей у электрического поля (2.7) и отсутствие носителей у магнитного поля (2.8).
Уравнением непрерывности называют дифференциальную форму закона сохранения заряда
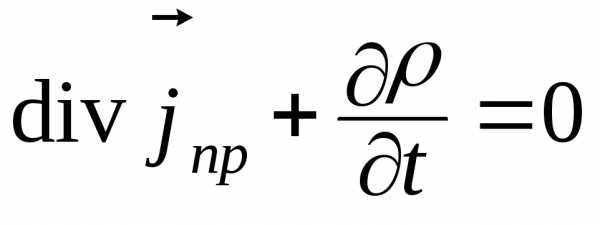 . (2.9)
. (2.9)
Из (2.9) следует, что в точках, являющихся источниками jпр , происходит убывание заряда [8]. Без введения тока смещения уравнения системы Максвелла и уравнение непрерывности не выполняются.
Уравнения Максвелла в комплексной форме. В радиотехнике часто используются гармонические колебания. В линейных системах удобно использовать метод комплексных амплитуд. В этом случае от реального сигнала cos (t+z) с помощью добавления мнимой составляющей isin (t+z) по формуле Л. Эйлера переходят к комплексному представлению сигнала exp (i(t+z)).
Когда анализ завершен, для получения окончательного ответа из комплексного результата достаточно выделить действительную часть.
В комплексной форме операции интегрирования и дифференцирования по времени существенно упрощаются
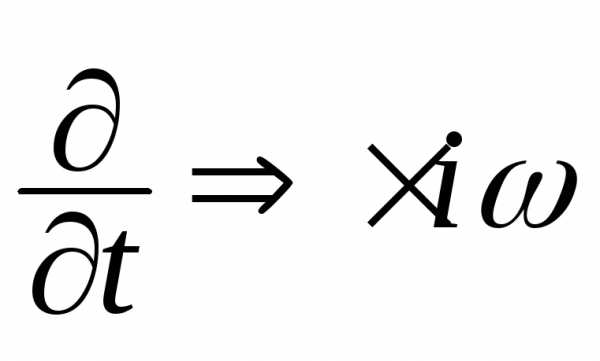 ;
; 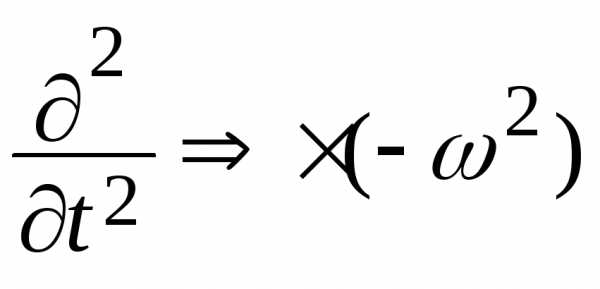 ;. (2.10)
;. (2.10)
Комплексную амплитуду (кроме амплитуды в нее входит и начальная фаза) будем обозначать точкой сверху. В комплексной форме уравнения (2.5) и (2.6) будут иметь вид
; (2.11)
; (2.12)
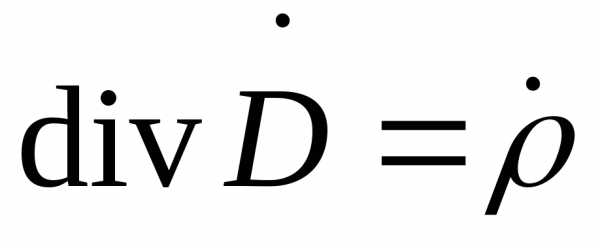 ,
, 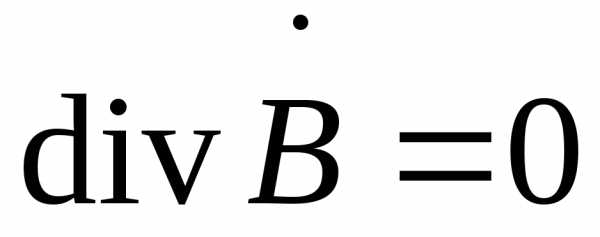 .
(2.13)
.
(2.13)
Введение 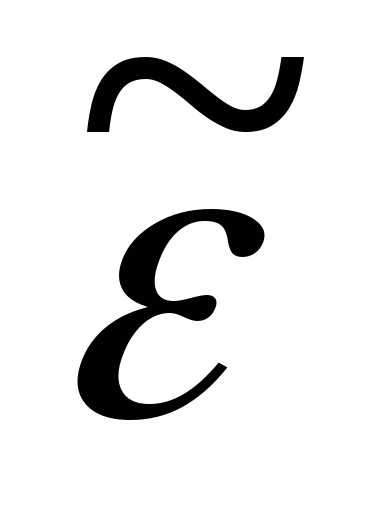 делает уравнения (2.11) и (2.12) похожими.
делает уравнения (2.11) и (2.12) похожими.
. (2.14)
Тангенс угла диэлектрических потерь. Для оценки соотношения между током проводимости и током смещения удобно ввести величину тангенс угла диэлектрических потерь
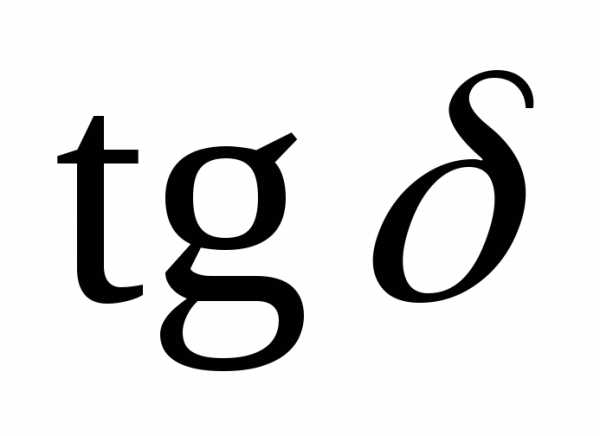 =
=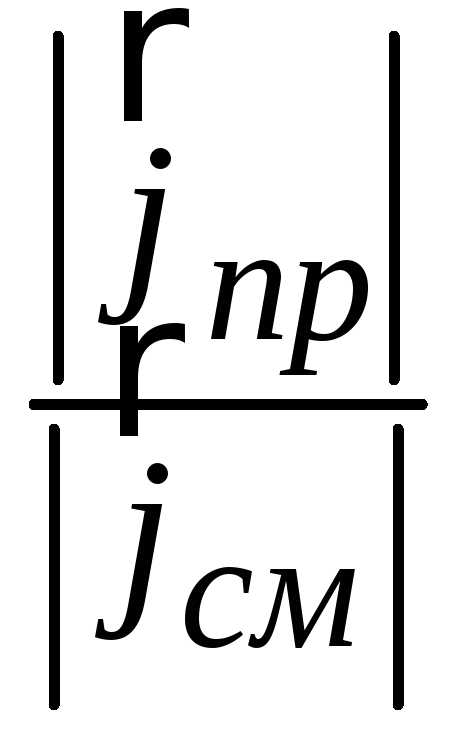 =
=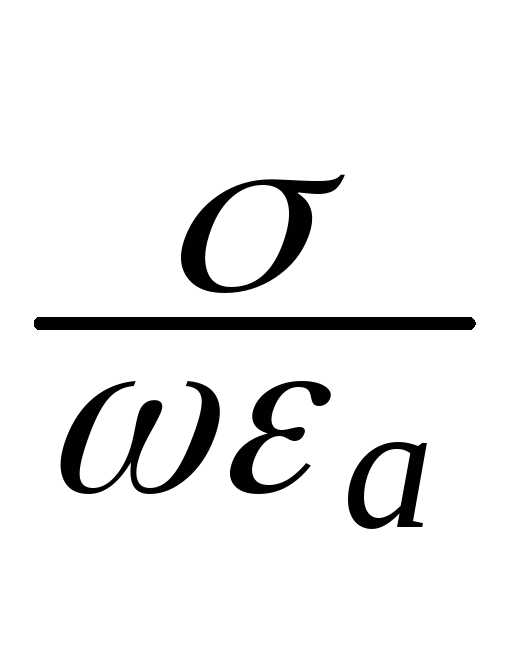 . (2.15)
. (2.15)
В зависимости от значения tg среды можно классифицировать так:
– диэлектрик;
– полупроводящая среда;
– проводник.
(2.16)Из уравнения (2.15) следует, что tg зависит от частоты. Это значит, что одно и то же вещество может на НЧ вести себя как проводник, а на ВЧ – как диэлектрик.
Например, морская вода с параметрами = 1 См/м и = 80 на частотах менее 23 МГц проявляет себя как проводник, а на частотах более 2,3 ГГц – как диэлектрик. Следует отметить, что такие типичные диэлектрики, как фарфор, эбонит, слюда, из-за очень малой проводимости ( <10–12 См/м) даже на очень низких частотах остаются диэлектриками, а металлы из-за очень высокой проводимости ( >106 См/м) остаются проводниками на высоких частотах вплоть до диапазона КВЧ.
При измерениях на высоких частотах tg обычно оказывается больше, чем результаты по уравнению (2.15). Это происходит в основном из-за влияния поляризационных потерь [1, 11], которые суммируются с tg (2.15). Для типичных радиодиэлектриков на высоких частотах именно данный вид потерь является преобладающим [2], поэтому более точным будет определение tg как отношения активной части плотности полного тока смещения к реактивной [1, 2]
, (2.17)
где Э – угол запаздывания по фазе  от
от [1, 2].
[1, 2].
Система уравнений Максвелла с учетом сторонних источников. В задачах электродинамики к сторонним источникам относят такие источники ЭМП, которые возбуждают это поле, но сами от него не зависят, так как их поддерживают сторонние по отношению к исследуемому ЭМП физические явления [11]. Например, при определении ЭМП вокруг проволочной антенны целесообразно исключить из анализа ЭМП генератор и линию передачи, которые вместе с антенной образуют единую электродинамическую систему, а влияние происходящих в них процессов учесть введением в систему плотности стороннего тока, что существенно упрощает решение задачи [11].
Таким образом, сторонние величины (jст, ст и т. п.) суммируются (или вычитаются, в зависимости от направления взаимодействия токов или полярностей зарядов) с соответствующими величинами системы уравнений Максвелла.
; ; (2.18)
; . (2.19)
В комплексной форме уравнения (2.18)–(2.19) будут иметь вид
; ; (2.20)
; . (2.21)
Индексы (м) указывают источники магнитного типа. Введение эквивалентных (физически фиктивных) магнитных зарядов и токов может упростить решение некоторых электродинамических задач.
Список рекомендуемой литературы: [1, гл. 3, с. 17–23; 2, с. 28–39; 3, гл. 1–2, с. 16–21; 4, с. 16–21; 5, с. 8–13, 17–18; 6, с. 7–41, 119–121; 7, с. 34–49; 8, с. 5–7; 9, с. 30–38, 51–56; 10, с. 19–38, 51–56; 11, с. 16–42, 48–52; 12, с. 26–37, 46–54; 13, с. 8–29, 36–39, 123–128; 15, с. 199–207; 31].
studfiles.net
Уравнения Максвелла в интегральной и дифференциальной форме
Введение тока смещения позволило Дж. Максвеллу создать теорию, которая объяснила все известные на тот момент явления из области электромагнетизма и позволила выдвинуть ряд новых гипотез, которые позднее были подтверждены.
В основу данной теории легли уравнения Максвелла, которые в электромагнетизме играют такую же роль, как начала в термодинамике или законы Ньютона в классической механике.
Уравнения Максвелла в дифференциальной форме.
В настоящей интерпретации система уравнений Максвелла имеет четыре структурных векторных уравнения:
Первое уравнение устанавливает связь между полным током (суммой тока проводимости и током смещения) и магнитным полем, которое они вызывают.
Второе уравнение является выражением закона электромагнитной индукции в интерпретации Максвелла (переменное магнитное поле – один из источников возникновения электрического поля).
Третье уравнение – указывает на факт отсутствия магнитных зарядов.
Четвертое уравнение говорит о том, что источниками электрического поля являются электрические заряды.
Уравнения (1) – (4) являются уравнениями Максвелла в дифференциальной форме. Каждое из векторных уравнений эквивалентно трем скалярным уравнениям, которые связывают компоненты векторов в правых и левых частях выражений.
Для того, чтобы применять систему уравнений Максвелла для расчета конкретных полей, уравнения данной системы дополняются материальными уравнениями, которые связывают векторы $\overrightarrow{D}\ и\ \overrightarrow{j}$ c вектором $\overrightarrow{E}$, а вектор $\overrightarrow{H}$ c вектором $\overrightarrow{B}$. Эти равнения имеют вид:
где величины $\varepsilon $,$\ \mu $, $\sigma $ — материальные постоянные, характеризующие свойства среды.
Если уравнения (1) – (4) являются фундаментальными, то относительно уравнений (5) надо отметить, что они выполняются совсем не всегда. Так, если речь идет о нелинейных явлениях, получение материальных уравнений составляет отдельную научную задачу.
Уравнения Максвелла в интегральной форме
Систему структурных уравнений Максвелла можно представить в интегральной форме. Так, если проинтегрировать уравнение (1) по произвольной поверхности $S$:
По теореме Стокса левая часть выражения (6) преобразуется к виду:
где интеграл в правой части берется по контуру $L$, который ограничивает поверхность $S$. Если считать, что контур и поверхность неподвижны, то операции дифференцирования по времени и интегрирования по поверхности можно поменять местами в выражении (6) левой части, получим:
здесь интеграл $\int\limits_S{\overrightarrow{D}d\overrightarrow{S}}$ является функцией только от времени, поэтому можно заменить частную производную обычной. Интегрируя уравнение (2) подобным образом, получим второе уравнение системы Максвелла:
Если проинтегрировать уравнение (3) по объему $V$, и использовать для преобразования левой части теорему Остроградского – Гаусса в интеграл по замкнутой поверхности $S$, которая ограничивает объем $V$, то получим:
Аналогичную процедуру проводят с уравнением (4). Получается:
Так получают систему уравнений Максвелла в интегральной форме:
Замечание
Уравнения Максвелла применимы к поверхностям любого размера. Эти уравнения описывают электрические и магнитные поля в покоящихся средах.
Пример 1
Задание: Ток, текущий по обмотке прямого соленоида, который имеет радиус $R$, изменяется так, что модуль индуктивности магнитного поля внутри соленоида растет в соответствии с законом: $B=Ct^2,\ $где $C=const.$ Запишите функцию тока смещения $j_{sm}\left(r\right),$ где $r$ — расстояние от оси соленоида.
Решение:
По определению, плотность тока смещения можно записать как:
\[j_{sm}=\frac{\partial D}{\partial t}\left(1.1\right).\]Используя одно из уравнений системы Максвелла:
\[\int\limits_S{\overrightarrow{E}d\overrightarrow{l}}=-\int\limits_S{\frac{\partial \overrightarrow{B}}{\partial t}d\overrightarrow{S}}\ (1.2),\]найдем напряженность электрического поля, которое порождается переменным магнитным полем, а зная связь напряжённости электрического поля и электрического смещения:
\[\overrightarrow{D}=\varepsilon {\varepsilon }_0\overrightarrow{E}(1.3)\]получим функцию $D(r)$.
Итак, используя уравнение изменения индукции магнитного поля из условий задачи, найдем частную производную $\frac{\partial \overrightarrow{B}}{\partial t}:$
\[\frac{\partial \overrightarrow{B}}{\partial t}=2Ct\left(1.4\right).\]Для $r \[2\pi rE=-\pi r^22Ct\to E=-rCt\to D=-C\varepsilon {\varepsilon }_0rt\to j_{sm}=-C\varepsilon {\varepsilon }_0r.\]
Для $r>R$, из (1.2) – (1.4) получим:
\[2\pi rE=-\pi R^22Ct,\ E=-C\frac{R^2t}{r}\to j_{sm}=-C\varepsilon {\varepsilon }_0\frac{R^2}{r}.\]Для $r=R$, из (1.2) – (1.4) найдем ток смещения:
\[E=-RCt\to D=-C\varepsilon {\varepsilon }_0Rt\to j_{sm}=-C\varepsilon {\varepsilon }_0R.\]Ответ: $j_{sm}=-C\varepsilon {\varepsilon }_0r\ \left(rR\right),\ j_{sm}=-C\varepsilon {\varepsilon }_0R\ \left(r=R\right).$
Пример 2
Задание: Запишите систему уравнений Максвелла для стационарных полей ($\overrightarrow{E}=const,\overrightarrow{H}=const\ $) в интегральной форме.
Решение:
В том случае, если поля стационарны, система уравнений максвелла распадается на две группы независимых уравнений. Первую группу составляют уравнения электростатики:
\[\int\limits_S{\overrightarrow{E}d\overrightarrow{l}}=0\ \ и\] \[\oint\limits_S{\overrightarrow{D}d\overrightarrow{S}=\int\limits_V{\rho }dV.}\]Вторая группа – уравнения магнитостатики:
\[\int\limits_L{\overrightarrow{H}d\overrightarrow{l}}=\int\limits_S{\overrightarrow{j}d\overrightarrow{S}}\ и\] \[\oint\limits_S{\overrightarrow{B}d\overrightarrow{S}=0}.\]spravochnick.ru
Уравнение Максвелла в интегральной и дифференциальной форме. Их физический смысл, некоторые свойства уравнений Максвелла.
Уравне́ния Ма́ксвелла — система уравнений в дифференциальной или интегральной форме, которые описывают электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца образуют полную систему уравнений классической электродинамики, называемую иногда уравнениями Максвелла — Лоренца. Уравнения, сформулированные Джеймсом Клерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее, влияние не только на все области физики, непосредственно связанные с электромагнетизмом, но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму (одним из ярчайших примеров здесь может служить специальная теория относительности).
Дифференциальная формаУравнения Максвелла представляют собой в векторной записи систему из четырёх уравнений, сводящуюся в компонентном представлении к восьми (два векторных уравнения содержат по три компоненты каждое плюс два скалярных[28]) линейных дифференциальных уравнений в частных производных первого порядка для 12 компонент четырёх векторных функций ( ):
Жирным шрифтом в дальнейшем обозначаются векторные величины, курсивом — скалярные. Введённые обозначения:
означает ротор вектора,
означает дивергенцию вектора.
Приведённые выше уравнения Максвелла не составляют ещё полной системы уравнений электромагнитного поля, поскольку они не содержат свойств среды, в которой возбуждено электромагнитное поле. Соотношения, связывающие величины , , , и и учитывающие индивидуальные свойства среды, называются материальными уравнениями.
Интегральная форма
При помощи формул Остроградского — Гаусса и Стокса дифференциальным уравнениям Максвелла можно придать форму интегральных уравнений:
Поток электрического поля через замкнутую поверхность
Введённые обозначения:
При интегрировании по замкнутой поверхности вектор элемента площади направлен из объёма наружу. Ориентация при интегрировании по незамкнутой поверхности определяется направлением правого винта, «вкручивающегося» при повороте в направлении обхода контурного интеграла по .
Словесное описание законов Максвелла, например, закона Фарадея, несёт отпечаток традиции, поскольку вначале при контролируемом изменении магнитного потока регистрировалось возникновение электрического поля (точнее электродвижущей силы). В общем случае в уравнениях Максвелла (как в дифференциальной, так и в интегральной форме) векторные функции являются равноправными неизвестными величинами, определяемыми в результате решения уравнений.
Рассмотрим физический смысл этих 4 уравнений: силовые линии электрического поля электромагнитной волны замкнуты, как и силовые линии магнитного поля.
Одно из уравнений гласит, что электрическое поле образуется зарядами и его силовые линии начинаются и заканчиваются на зарядах.
Другое уравнение описывает магнитные силовые линии — это кольцеобразные замкнутые линии.
Третье уравнение представляет собой общий случай закона электромагнитной индукции Фарадей: любое изменение магнитного поля генерирует в соответствии с этим уравнением вихревое электрическое поле.
Четвертое уравнение. До Максвелла была известно часть этого уравнения, которая годилась для постоянных токов — это закон Ампера, утверждающий, что текущие по проводам электрические заряды (т.е. постоянный ток) создают определяемое уравнением Ампера магнитное поле.
Связав с помощью уравнений открытые до него законы, Максвелл увидел, что система несовершенна. Чтобы система имела решение, Максвелл добавил в четвертое уравнение одно слагаемое, а именно к току движущихся зарядов (ток проводимости) добавил воображаемый им ток смещения. Так он назвал изменяющееся во времени электрическое поле.
Ток смещения подобно электрическому току зарядов порождает магнитное поле. Т.об. Максвелл ввел в уравнение Ампера слагаемое, которое убывает. Это волновое слагаемое — часть поля, которое угасает гараздо медленнее обратного квадрата расстояния.
17. Свободные колебания в колебательном контуре. Дифференциальное уравнение затухающих электромагнитных колебаний и его решения.
Свободные колебания — колебания в системе под действием внутренних тел, после того как система выведена из положения равновесия.
Колебания груза, подвешенного на нити, или груза, прикрепленного к пружине, — это примеры свободных колебаний. После выведения этих систем из положения равновесия создаются условия, при которых тела колеблются без воздействия внешних сил.
Система — группа тел, движение которых мы изучаем.
Внутренние силы — силы, действующие между телами системы.
Внешние силы — силы, действующие на тела системы со стороны тел, не входящих в нее.
Условия возникновения свободных колебаний.
При выведении тела из положения равновесия в системе должна возникать сила, направленная к положению равновесия и, следовательно, стремящаяся возвратить тело в положение равновесия.
Пример: при перемещении шарика, прикрепленного к пружине, влево и при его перемещении вправо сила упругости направлена к положению равновесия.
Трение в системе должно быть достаточно мало. Иначе колебания быстро затухнут или вовсе не возникнут. Незатухающие колебания возможны лишь при отсутствии трения.
Если рассматривать колебательный контур, то для получения вынужденных колебаний (рис. 8.4), нужно включить последовательно с элементами контура переменную эдс или, разорвав контур, подать напряжение:
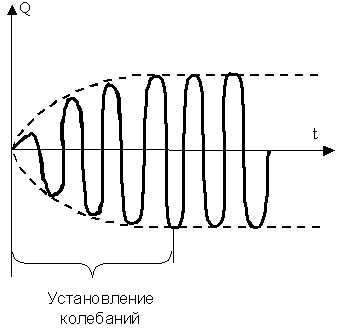
Рис. 8.4. Вынужденные колебания в колебательном контуре
U = Umcosw, тогда уравнение будет иметь вид:
<!–[if !supportEmptyParas]–> <!–[endif]–> <!–[if !vml]–><!–[endif]–>, (8.15)
<!–[if !supportEmptyParas]–> <!–[endif]–>
после замены получим
<!–[if !supportEmptyParas]–> <!–[endif]–> <!–[if !vml]–><!–[endif]–>. (8.16)
Решение полученного неоднородного дифференциального уравнения находим прибавлением к его частному решению общего решения соответствующего однородного уравнения. Частное решение имеет вид
<!–[if !vml]–><!–[endif]–>,
где <!–[if !vml]–><!–[endif]–>.
Подставив в эти выражения значения <!–[if !vml]–> <!–[endif]–>, получим:
<!–[if !supportEmptyParas]–> <!–[endif]–> <!–[if !vml]–><!–[endif]–>. (8.17)
<!–[if !supportEmptyParas]–> <!–[endif]–>Разделив заряд на емкость, получим напряжение на конденсаторе:
<!–[if !vml]–><!–[endif]–>,
где <!–[if !vml]–><!–[endif]–>. Установившийся ток в контуре <!–[if !vml]–> <!–[endif]–>. Амплитуда тока имеет вид
<!–[if !supportEmptyParas]–> <!–[endif]–> <!–[if !vml]–><!–[endif]–>. (8.18)
<!–[if !supportEmptyParas]–> <!–[endif]–>
Резонансная частота для контура
<!–[if !supportEmptyParas]–> <!–[endif]–> <!–[if !vml]–><!–[endif]–> <!–[if !vml]–><!–[endif]–>. (8.19)
Резонансные кривые для UCи тока I имеют такой вид, как показано на рис. 8.5.
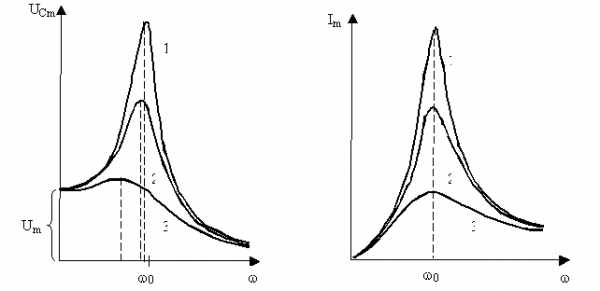
Рис. 8.5. Явление резонанса напряжений и токов в колебательном контуре: кривые 1, 2, 3 соответствуют всё бóльшему активному сопротивлению контура
<!–[if !supportEmptyParas]–> <!–[endif]–>
При <!–[if !vml]–> <!–[endif]–> резонансные кривые стремятся к Um – напряжению, возникающему на конденсаторе при подключению его к источнику постоянного напряжения. Максимум при резонансе получается тем выше и острее, чем меньше <!–[if !vml]–> <!–[endif]–>, т. е. чем меньше активное сопротивление и больше индуктивность контура. Тогда амплитуда силы тока имеет максимальное значение при <!–[if !vml]–> <!–[endif]–>. Следовательно, резонансная частота для силы тока совпадает с собственной частотой контура <!–[if !vml]–> <!–[endif]–>.
cyberpedia.su
2. Уравнение Максвелла в дифференциальной форме.
Уравнения (3-6) записаны в интегральной форме. Гораздо чаще используется дифференциальная форма записи этих уравнений, которая позволяет описать электромагнитное поле в любой точке (точнее в любом элементарном объёме) пространства. Уравнения Максвелла в дифференциальной форме легко получаются из уравнений (3-6) путём применения известных из векторного анализа теорем Остроградского-Гаусса и Стокса, устанавливающих связь между линейными, поверхностными и объёмными интегралами:
Теорема Остроградского-Гауса связывает объёмный интеграл с поверхностным | , |
где – скалярная функция – дивергенция (расхождение):
Теорема Стокса связывает поверхностный интеграл с линейным | , |
где – векторная функция – ротор (вихрь):
С учётом вышеизложенного уравнения (3-6) принимают вид:
Т.к. объёмы и поверхности, по которым происходит интегрирование произвольны, то можно приравнять подынтегральные функции и получить уравнения Максвелла в дифференциальной форме:
Уравнения Максвелла в дифференциальной форме | (7) (8) (9) (10) |
3. Материальные уравнения.
Уравнения Максвелла ещё не составляют полной системы уравнений электромагнитного поля. Этих уравнений недостаточно для нахождения полей по заданным распределениям зарядов и токов. Для этого необходимо дополнить соотношения, в которые входили бы величины, характеризующие индивидуальные свойства среды. Для случая изотропных сред (не содержащих сегнетоэлектриков и ферромагнетиков) они имеют следующий вид:
(11)
С учётом соотношений (11) система уравнений является полной и позволяет описывать все электромагнитные процессы в вакууме и веществе.
4. Свойства уравнений Максвелла.
А. Уравнения Максвелла линейны. Они содержат только первые производные полей и по времени и пространственным координатам, а так же первые степени плотности электрических зарядов ρ и токов γ. Свойство линейности уравнений непосредственно связано с принципом суперпозиции.
Б. Уравнения Максвелла содержат уравнение непрерывности, выражающее закон сохранения электрического заряда:
В. Уравнения Максвелла выполняются во всех инерциальных системах отсчёта. Они являются релятивистски-инвариантными, что подтверждается опытными данными.
Г. О симметрии уравнений Максвелла.
Уравнения не симметричны относительно электрического и магнитного полей. Это обусловлено тем, что в природе существуют электрические заряды, но нет магнитных зарядов. Вместе с тем в нейтральной однородной среде, где ρ = 0 и ,уравнения Максвелла приобретают симметричный вид, т.е. так связано с , как с .
Различие только в знаках перед производными и показывает, что линии вихревого электрического поля, индуцированного уменьшением поля , образуют с вектором левовинтовую систему, в то время как линии магнитного поля, индуцируемого изменением , образуют с вектором правовинтовую систему. |
Д. Об электромагнитных волнах.
Из уравнений Максвелла следует важный вывод о существовании принципиально нового физического явления: электромагнитное поле способно существовать самостоятельно без электрических зарядов и токов. При этом изменение его состояния обязательно имеет волновой характер. Всякое изменение во времени магнитного поля возбуждает поле электрическое, изменение электрического поля, в свою очередь, возбуждает магнитное поле. За счёт непрерывного взаимопревращения они и должны сохранятся. Поля такого рода называются электромагнитными волнами. Выяснилось также, что ток смещения играет в этом явлении первостепенную роль.
studfiles.net

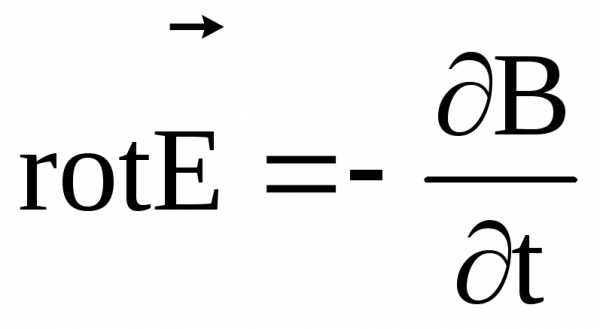 (7)
(7)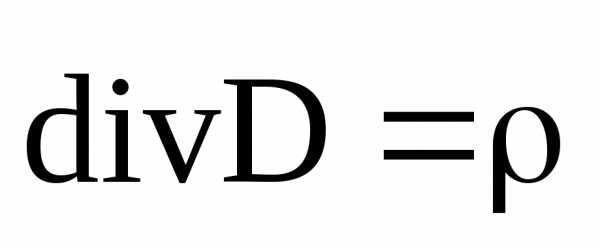 (8)
(8)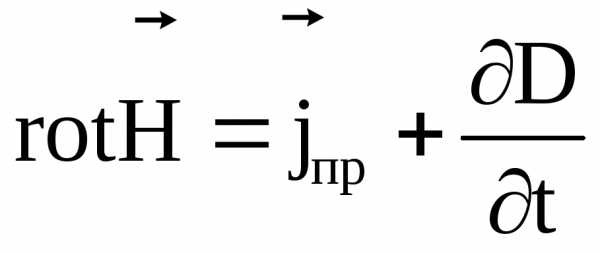
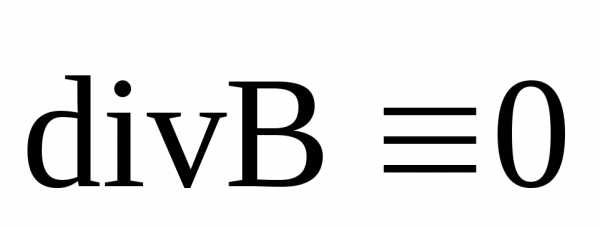 (10)
(10)

