Ускорение формула точки – Напишите формулу для определения касательного ускорения точки. Что оно собой характеризует? Укажите, в каких случаях оно равно нулю?
- Комментариев к записи Ускорение формула точки – Напишите формулу для определения касательного ускорения точки. Что оно собой характеризует? Укажите, в каких случаях оно равно нулю? нет
- Советы абитуриенту
- Ускорение точки
- Кинематика материальной точки
- 1.5 Скорость и ускорение точки при естественном способе изучения движения точки
- Скорость и ускорение точек тела. Формула Ривальса
- Сложное движение точки Теорема Кориолиса
- Скорость и ускорение точек твердого тела
- 3.2. Вычисление абсолютной скорости и абсолютного ускорения точки
Ускорение точки
Пусть теперь
известна функция 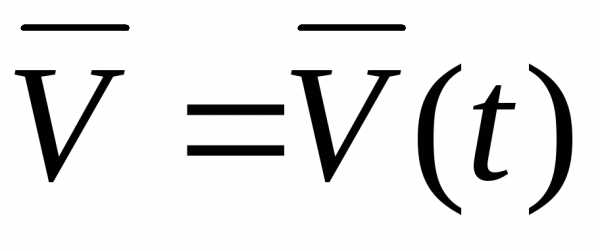 .
На рис. 5.10
.
На рис. 5.10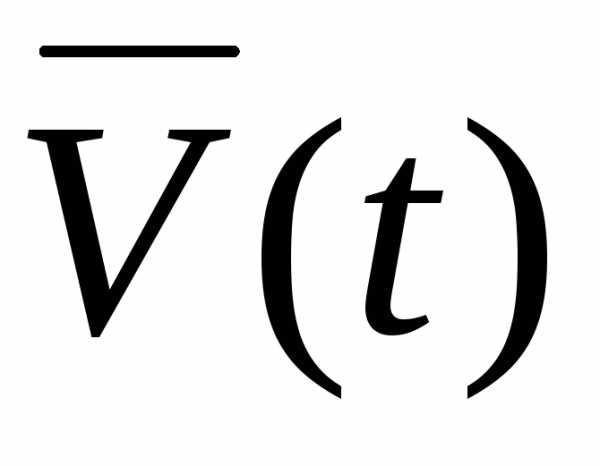 и
и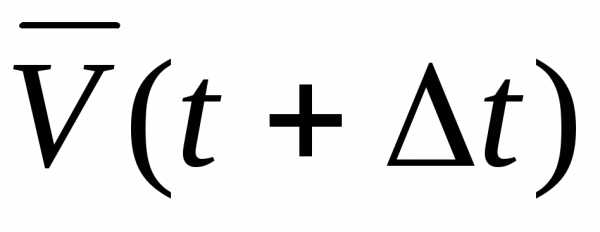
векторы скорости движущейся точки в
моменты t и t.
Чтобы получить приращение вектора
скорости
векторы скорости движущейся точки в
моменты t и t.
Чтобы получить приращение вектора
скорости 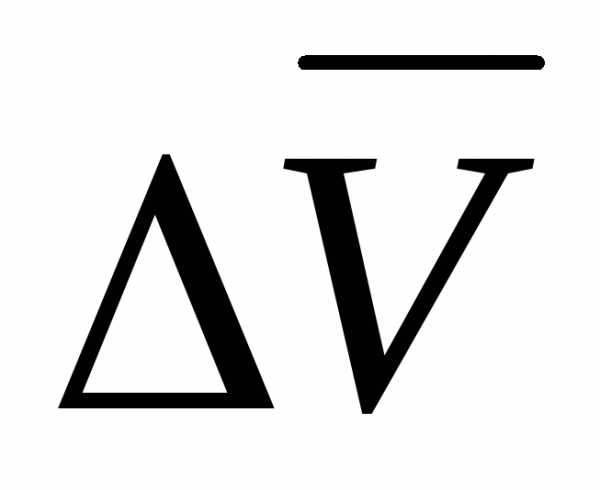 перенесем параллельно вектор
перенесем параллельно вектор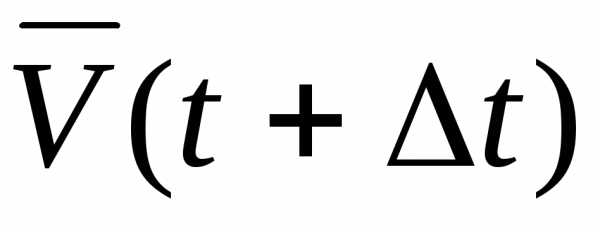 в точкуМ:
в точкуМ:
Средним ускорением
точки за промежуток времени t называется
отношение приращения вектора скорости 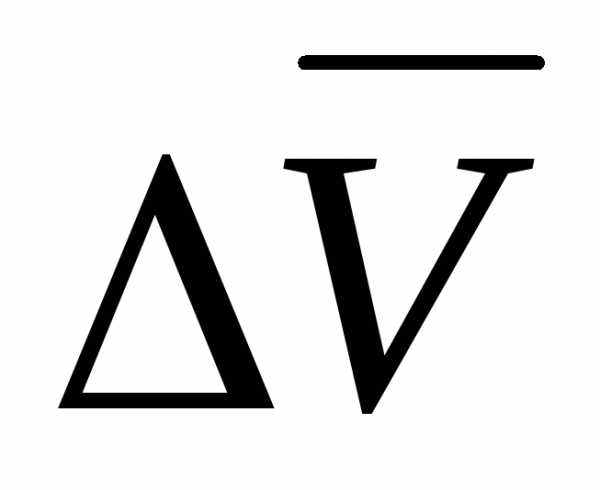 к промежутку времениt:
к промежутку времениt:
Следовательно, ускорение точки в данный момент времени равно первой производной по времени от вектора скорости точки или второй производной радиус-вектора по времени
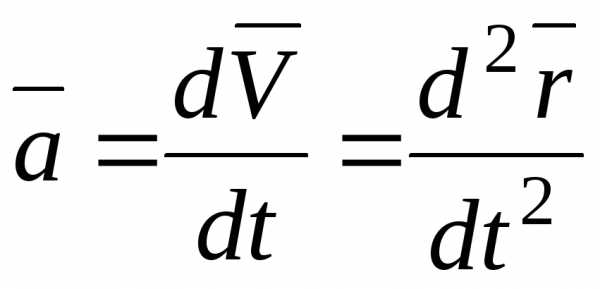 .
(5.11)
.
(5.11)
Ускорение точки это векторная величина, характеризующая быстроту изменения вектора скорости по времени.
Построим годограф скорости (рис.5.11). Годографом скорости по определению является кривая, которую вычерчивает конец вектора скорости при движении точки, если вектор скорости откладывается из одной и той же точки.
Рис.5.11 | Очевидно, что скорость точки, вычерчивающей годограф скорости, будет равна ускорению точки при ее движении по траектории. Единицей измерения ускорения в системе Си является м/с 2. |
Определение скорости точки при координатном способе задания её движения
Пусть движение точки задано координатным способом в декартовой системе координат
х = x(t), y = y(t), z = z(t)
Радиусвектор точки равен
.
Так как единичные
векторы 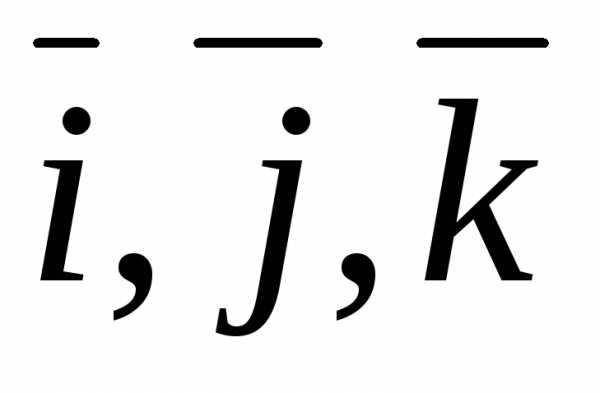 постоянны, то по определению
постоянны, то по определению
. (5.12)
Обозначим проекции вектора скорости на оси Ох, Оу и Oz через Vx, Vy, Vz соответственно и разложим вектор скорости по осям:
(5.13)
Сравнивая равенства (5.12) и (5.13) получим
 (5.14)
(5.14)
В дальнейшем производную по времени будем обозначать точкой сверху, т.е.
.
Модуль скорости точки определяется формулой
. (5.15)
Направление вектора скорости определяется направляющими косинусами:
Определение ускорения точки при координатном способе задания её движения
Вектор скорости в декартовой системе координат равен
.
По определению
. (5.16)
Обозначим проекции вектора ускорения на оси Ох, Оу и Oz через аx, аy, аz соответственно и разложим вектор скорости по осям:
. (5.17)
Сравнивая равенства (5.16) и (5.17) получим
. (5.18)
Модуль вектора ускорения точки вычисляется аналогично модулю вектора скорости точки:
, (5.19)
а направление вектора ускорения направляющими косинусами:
Определение скорости и ускорения точки при естественном способе задания её движения
Орты  и
и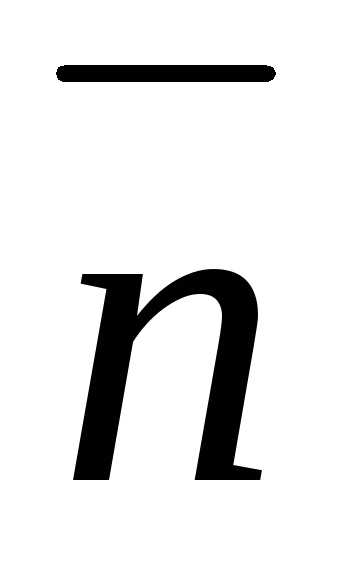 лежат всоприкасающейся
плоскости,
орты
лежат всоприкасающейся
плоскости,
орты 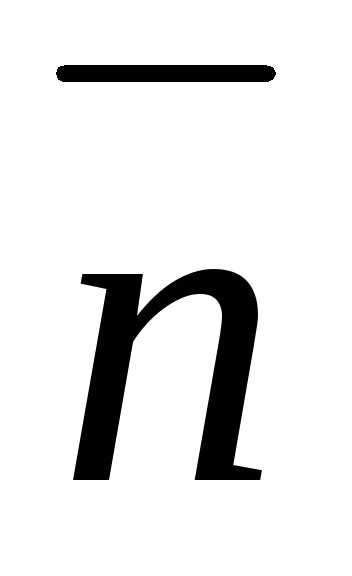 и
и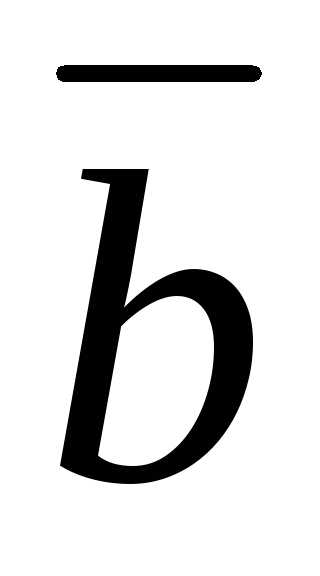 внормальной
плоскости,
орты
и
внормальной
плоскости,
орты
и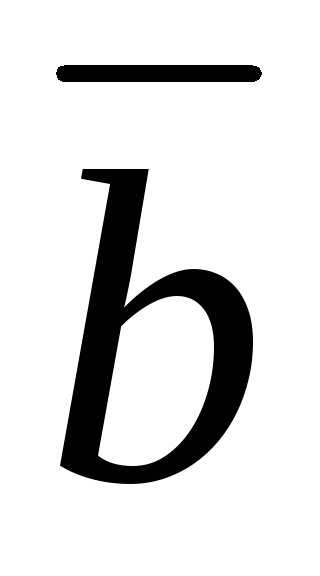
в спрямляющей
плоскости.
в спрямляющей
плоскости.
Полученный трехгранник называется естественным.
Пусть задан закон движения точки s = s(t).
Радиус вектор 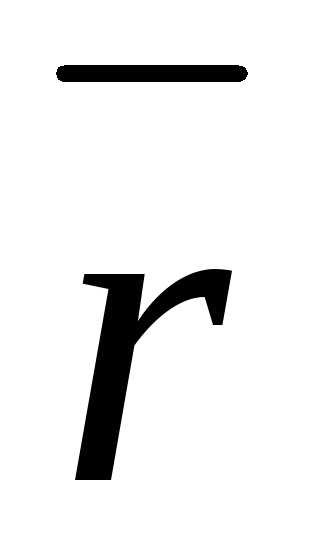 точкиМ относительно какойлибо
фиксированной точки будет сложной
функцией времени
.
точкиМ относительно какойлибо
фиксированной точки будет сложной
функцией времени
.
Из дифференциальной геометрии известны формулы СерреФрене, устанавливающие связи между единичными векторами естественных осей и векторфункцией кривой

где радиус кривизны траектории.
Используя определение скорости и формулы СерреФрене, получим:
. (5.20)
Обозначая проекцию
скорости на касательную 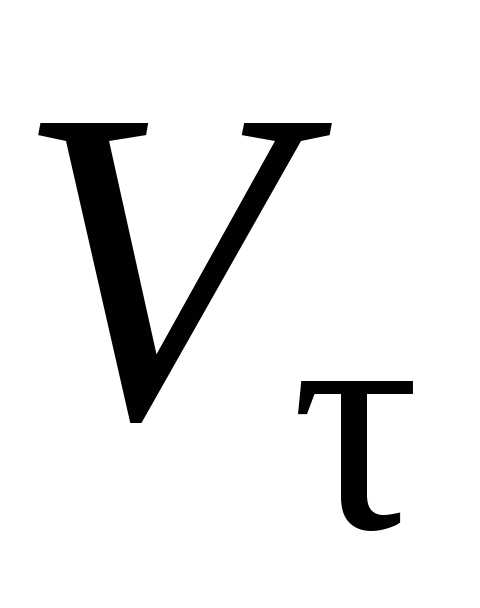 и учитывая, что вектор скорости направлен
по касательной, имеем
и учитывая, что вектор скорости направлен
по касательной, имеем
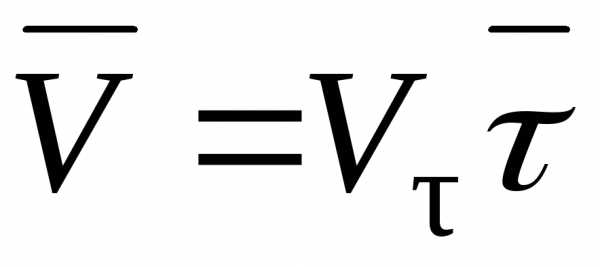 . (5.21)
. (5.21)
Сравнивая равенства (5.20) и (5.21), получим формулы для определения вектора скорости по величине и направлению
. (5.22)
Величина 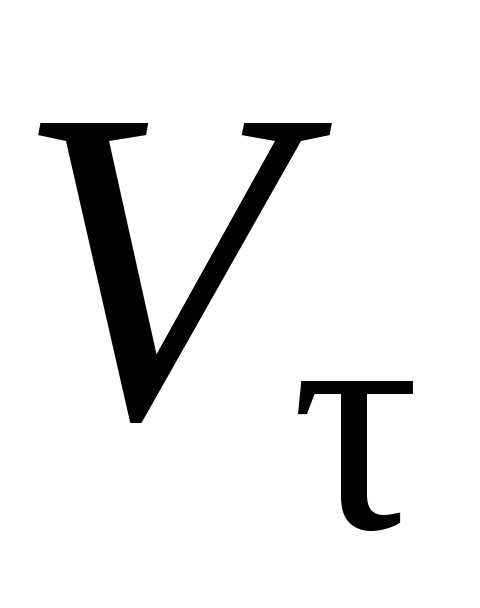
Используя определение ускорения и формулы СерреФрене, получим:
(5.23)
Обозначим проекцию
ускорения точки  на касательную
на касательную ,
главную нормаль и бинормаль
,
главную нормаль и бинормаль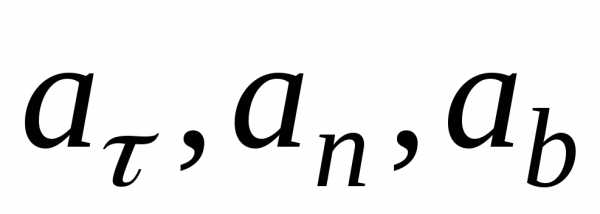 соответственно.
соответственно.
Тогда ускорение равно
(5.24)
Из формул (5.23) и
(5.24) следует, что вектор ускорения всегда
лежит в соприкасающейся плоскости и
раскладывается по направлениям  и
и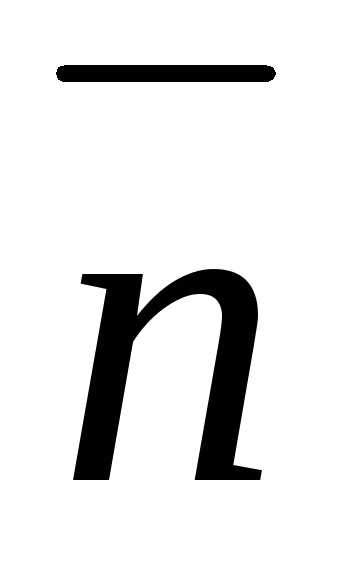 :
:
(5.25)
Проекция ускорения
на касательную 
Проекция ускорения
на главную нормаль 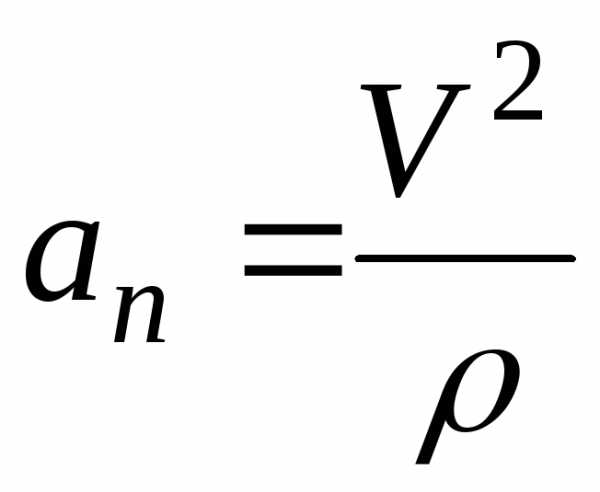 называетсянормальным
ускорением.
Оно характеризует изменение вектора
скорости по направлению.
называетсянормальным
ускорением.
Оно характеризует изменение вектора
скорости по направлению.
Модуль вектора ускорения равен .
Если  и
и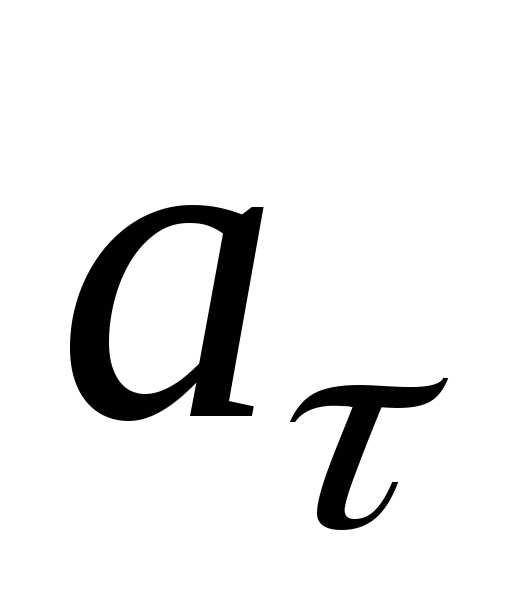 одного знака, то движение точки будет
ускоренным.
одного знака, то движение точки будет
ускоренным.
Если  и
и разных знаков, то движение точки будет
замедленным.
разных знаков, то движение точки будет
замедленным.
studfiles.net
Кинематика материальной точки
Основные формулы кинематики материальной точки
Приведем основные формулы кинематики материальной точки. После чего дадим их вывод и изложение теории.
Радиус-вектор материальной точки M в прямоугольной системе координат Oxyz:
,
где – единичные векторы (орты) в направлении осей x, y, z.
Скорость точки:
;
.
.
Единичный вектор в направлении касательной к траектории точки:
.
Ускорение точки:
;
;
;
; ;
Тангенциальное (касательное) ускорение:
;
;
.
Нормальное ускорение:
;
;
.
Единичный вектор, направленный к центру кривизны траектории точки (вдоль главной нормали):
.
Радиус кривизны траектории:
.
Далее приводится вывод этих формул и изложение теории кинематики материальной точки.
Радиус-вектор и траектория точки
Рассмотрим движение материальной точки M. Выберем неподвижную прямоугольную систему координат Oxyz с центром в некоторой неподвижной точке O. Тогда положение точки M однозначно определяются ее координатами (x, y, z). Эти координаты являются компонентами радиус-вектора материальной точки.
Радиус-вектор точки M – это вектор , проведенный из начала неподвижной системы координат O в точку M.
,
где – единичные векторы в направлении осей x, y, z.
При движении точки, координаты изменяются со временем . То есть они являются функциями от времени . Тогда систему уравнений
(1)
можно рассматривать как уравнение кривой, заданной параметрическими уравнениями. Такая кривая является траекторией точки.
Траектория материальной точки – это линия, вдоль которой происходит движение точки.
Если движение точки происходит в плоскости, то можно выбрать оси и системы координат так, чтобы они лежали в этой плоскости. Тогда траектория определяется двумя уравнениями
В некоторых случаях, из этих уравнений можно исключить время . Тогда уравнение траектории будет иметь зависимость вида:
,
где – некоторая функция. Эта зависимость содержит только переменные и . Она не содержит параметр .
Скорость материальной точки
Скорость материальной точки – это производная ее радиус-вектора по времени.
Согласно определению скорости и определению производной:
Производные по времени, в механике, обозначают точкой над символом. Подставим сюда выражение для радиус-вектора:
,
где мы явно обозначили зависимость координат от времени. Получаем:
,
где
,
,
– проекции скорости на оси координат. Они получаются дифференцированием по времени компонент радиус-вектора
.
Таким образом
.
Модуль скорости:
.
Касательная к траектории
С математической точки зрения, систему уравнений (1) можно рассматривать как уравнение линии (кривой), заданной параметрическими уравнениями. Время , при таком рассмотрении, играет роль параметра. Из курса математического анализа известно, что направляющий вектор для касательной к этой кривой имеет компоненты:
.
Но это есть компоненты вектора скорости точки. То есть скорость материальной точки направлена по касательной к траектории.
Касательная к траектории точки
Все это можно продемонстрировать непосредственно. Пусть в момент времени точка находится в положении с радиус-вектором (см. рисунок). А в момент времени – в положении с радиус-вектором . Через точки и проведем прямую . По определению, касательная – это такая прямая , к которой стремится прямая при .
Введем обозначения:
;
;
.
Тогда вектор направлен вдоль прямой .
При стремлении , прямая стремится к касательной , а вектор – к скорости точки в момент времени :
.
Поскольку вектор направлен вдоль прямой , а прямая при , то вектор скорости направлен вдоль касательной .
То есть вектор скорости материальной точки направлен вдоль касательной к траектории.
Введем направляющий вектор касательной единичной длины:
.
Покажем, что длина этого вектора равна единице. Действительно, поскольку
, то:
.
Тогда вектор скорости точки можно представить в виде:
.
Далее мы считаем, что если над буквой векторной величины не стоит стрелка, то это обозначает модуль вектора.
Ускорение материальной точки
Ускорение материальной точки – это производная ее скорости по времени.
Аналогично предыдущему, получаем компоненты ускорения (проекции ускорения на оси координат):
;
;
;
.
Модуль ускорения:
.
Тангенциальное (касательное) и нормальное ускорения
Теперь рассмотрим вопрос о направлении вектора ускорения по отношению к траектории. Для этого применим формулу:
.
Дифференцируем ее по времени, применяя правило дифференцирования произведения:
.
Вектор направлен по касательной к траектории. В какую сторону направлена его производная по времени ?
Чтобы ответить на этот вопрос, воспользуемся тем, что длина вектора постоянна и равна единице. Тогда квадрат его длины тоже равен единице:
.
Здесь и далее, два вектора в круглых скобках обозначают скалярное произведение векторов. Продифференцируем последнее уравнение по времени:
;
;
.
Поскольку скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны друг другу. Так как вектор направлен по касательной к траектории, то вектор перпендикулярен к касательной.
Первую компоненту называют тангенциальным или касательным ускорением:
.
Вторую компоненту называют нормальным ускорением:
.
Тогда полное ускорение:
(2) .
Эта формула представляет собой разложение ускорения на две взаимно перпендикулярные компоненты – касательную к траектории и перпендикулярную к касательной.
Поскольку , то
(3) .
Тангенциальное (касательное) ускорение
Умножим обе части уравнения (2) скалярно на :
.
Поскольку , то . Тогда
;
.
Здесь мы положили:
.
Отсюда видно, что тангенциальное ускорение равно проекции полного ускорения на направление касательной к траектории или, что тоже самое, на направление скорости точки.
Тангенциальное (касательное) ускорение материальной точки – это проекция ее полного ускорения на направление касательной к траектории (или на направление скорости).
Символом мы обозначаем вектор тангенциального ускорения, направленный вдоль касательной к траектории. Тогда – это скалярная величина, равная проекции полного ускорения на направление касательной. Она может быть как положительной, так и отрицательной.
Подставив , имеем:
.
Подставим в формулу:
.
Тогда:
.
То есть тангенциальное ускорение равно производной по времени от модуля скорости точки. Таким образом, тангенциальное ускорение приводит к изменению абсолютной величины скорости точки. При увеличении скорости, тангенциальное ускорение положительно (или направлено вдоль скорости). При уменьшении скорости, тангенциальное ускорение отрицательно (или направлено противоположно скорости).
Радиус кривизны траектории
Теперь исследуем вектор .
Радиус кривизны траектории
Рассмотрим единичный вектор касательной к траектории . Поместим его начало в начало системы координат. Тогда конец вектора будет находиться на сфере единичного радиуса. При движении материальной точки, конец вектора будет перемещаться по этой сфере. То есть он будет вращаться вокруг своего начала. Пусть – мгновенная угловая скорость вращения вектора в момент времени . Тогда его производная – это скорость движения конца вектора. Она направлена перпендикулярно вектору . Применим формулу для вращающегося движения. Модуль вектора:
.
Теперь рассмотрим положение точки для двух близких моментов времени. Пусть в момент времени точка находится в положении , а в момент времени – в положении . Пусть и – единичные векторы, направленные по касательной к траектории в этих точках. Через точки и проведем плоскости, перпендикулярные векторам и . Пусть – это прямая, образованная пересечением этих плоскостей. Из точки опустим перпендикуляр на прямую . Если положения точек и достаточно близки, то движение точки можно рассматривать как вращение по окружности радиуса вокруг оси , которая будет мгновенной осью вращения материальной точки. Поскольку векторы и перпендикулярны плоскостям и , то угол между этими плоскостями равен углу между векторами и . Тогда мгновенная скорость вращения точки вокруг оси равна мгновенной скорости вращения вектора :
.
Здесь – расстояние между точками и .
Таким образом мы нашли модуль производной по времени вектора :
.
Как мы указали ранее, вектор перпендикулярен вектору . Из приведенных рассуждений видно, что он направлен в сторону мгновенного центра кривизны траектории. Такое направление называется главной нормалью.
Нормальное ускорение
Нормальное ускорение
направлено вдоль вектора . Как мы выяснили, этот вектор направлен перпендикулярно касательной, в сторону мгновенного центра кривизны траектории.
Пусть – единичный вектор, направленный от материальной точки к мгновенному центру кривизны траектории (вдоль главной нормали). Тогда
;
.
Поскольку оба вектора и имеют одинаковое направление – к центру кривизны траектории, то
.
Из формулы (2) имеем:
(4) .
Из формулы (3) находим модуль нормального ускорения:
.
Умножим обе части уравнения (2) скалярно на :
(2) .
.
Поскольку , то . Тогда
;
.
Отсюда видно, что модуль нормального ускорения равен проекции полного ускорения на направление главной нормали.
Нормальное ускорение материальной точки – это проекция ее полного ускорения на направление, перпендикулярное к касательной к траектории.
Подставим . Тогда
.
То есть нормальное ускорение вызывает изменение направления скорости точки, и оно связано с радиусом кривизны траектории.
Отсюда можно найти радиус кривизны траектории:
.
И в заключении заметим, что формулу (4) можно переписать в следующем виде:
.
Здесь мы применили формулу для векторного произведения трех векторов:
,
в которую подставили
.
Итак, мы получили:
;
.
Приравняем модули левой и правой частей:
.
Но векторы и взаимно перпендикулярны. Поэтому
.
Тогда
.
Это известная формула из дифференциальной геометрии для кривизны кривой.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
1.5 Скорость и ускорение точки при естественном способе изучения движения точки
Прежде чем определить кинематические характеристики точки при естественном способе, необходимо ввести так называемые естественные (натуральные) оси координат.
 Рассмотрим
некоторую пространственную кривую АВ,
которая является траекторией изучаемой
нами точки. Точки М и М1 – два соседних положения этой точки
(рис. 1.12). Проведем в этих точках касательные
к кривой, орты которых обозначены
Рассмотрим
некоторую пространственную кривую АВ,
которая является траекторией изучаемой
нами точки. Точки М и М1 – два соседних положения этой точки
(рис. 1.12). Проведем в этих точках касательные
к кривой, орты которых обозначены  и
и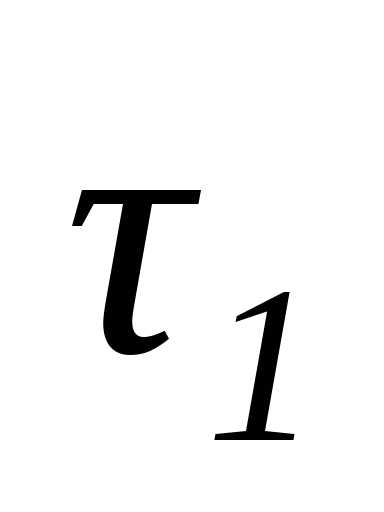 .
.
Перенесем
вектор 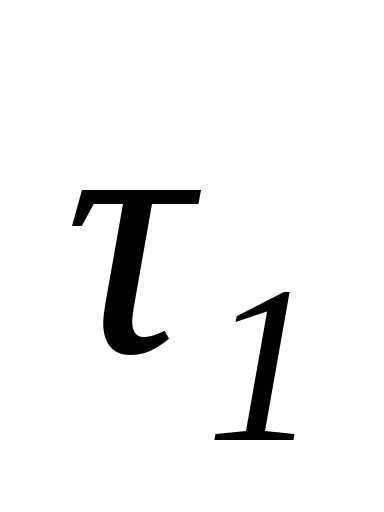 параллельно себе в точкуМ и через векторы
параллельно себе в точкуМ и через векторы 
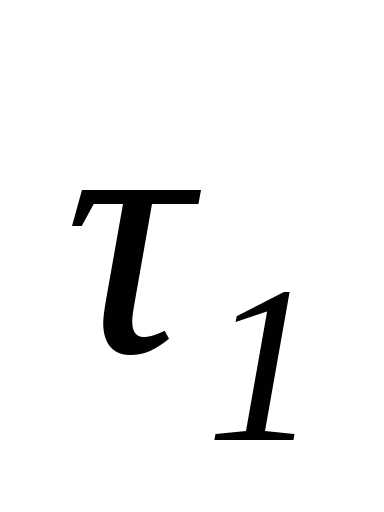 проведем плоскость. Граничное положение
этой плоскости при приближении точкиМ1 к точке М называется соприкасающейся
плоскостью (плоскость I).
Через точку М перпендикулярно к касательной
проведем плоскость. Граничное положение
этой плоскости при приближении точкиМ1 к точке М называется соприкасающейся
плоскостью (плоскость I).
Через точку М перпендикулярно к касательной  проведем плоскость, которая называетсянормальной
плоскостью (плоскость II).
Очевидно, что любая прямая, лежащая в
этой плоскости, будет перпендикулярной
к
проведем плоскость, которая называетсянормальной
плоскостью (плоскость II).
Очевидно, что любая прямая, лежащая в
этой плоскости, будет перпендикулярной
к  .
Линия пересечения соприкасающейся и
нормальной плоскостей называетсяглавной
нормалью кривой.
Единичный вектор этой оси обозначим
.
Линия пересечения соприкасающейся и
нормальной плоскостей называетсяглавной
нормалью кривой.
Единичный вектор этой оси обозначим 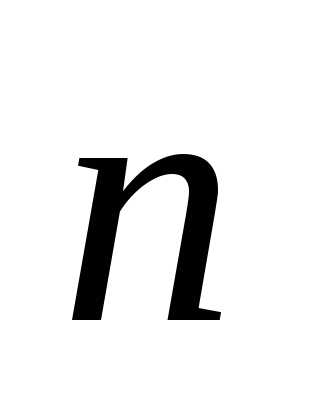 .
Нормаль, перпендикулярная к главной
нормали, называетсябинормалью
кривой.
.
Нормаль, перпендикулярная к главной
нормали, называетсябинормалью
кривой.В частности, если кривая – плоская, то соприкасающейся плоскостью будет плоскость, в которой лежит кривая, а главной нормалью – нормаль кривой, лежащая в этой плоскости.
Так называемый натуральный триэдр (трехосник) кривой образует совокупность трех взаимно перпендикулярных осей:
1) касательной Mτ, направленной в сторону возрастания дуги при движении точки (например, из точки О на рис. 1.12),
2) главной нормали Mn, направленной в сторону вогнутости кривой,
3) бинормали Mb, направленной по отношению к касательной и главной нормали так же, как ось Мz расположена по отношению к осям Мx и My в правой декартовой системе координат.
Обратим внимание
на то, что естественные оси координат
имеют начало в движущейся точке, движутся
они вместе с точкой, оставаясь взаимно
перпендикулярными. Поэтому единичные
векторы 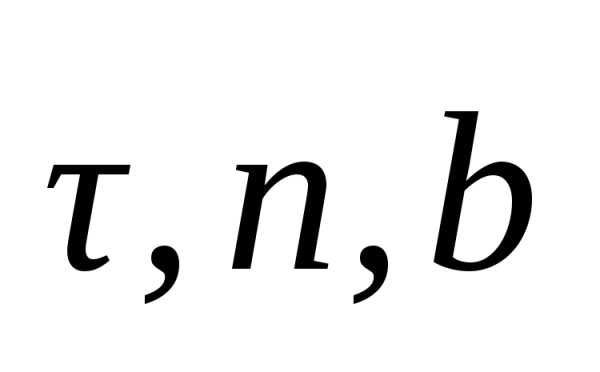 имеют постоянный модуль, но переменное
направление.
имеют постоянный модуль, но переменное
направление.
Перейдем к определению скорости точки при естественном способе изучения движения точки, воспользовавшись формулой (1.7), помня при этом, что каждому значению дуговой координаты
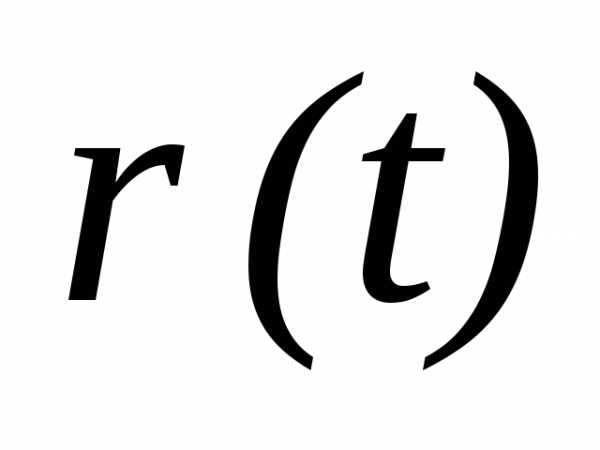 (рис. 1.13). Учитывая, что нам известна
функцияS (t),
формулу скорости (1.7) можно записать
следующим образом:
(рис. 1.13). Учитывая, что нам известна
функцияS (t),
формулу скорости (1.7) можно записать
следующим образом:. (1.16)
Выясним,
чему равна производная 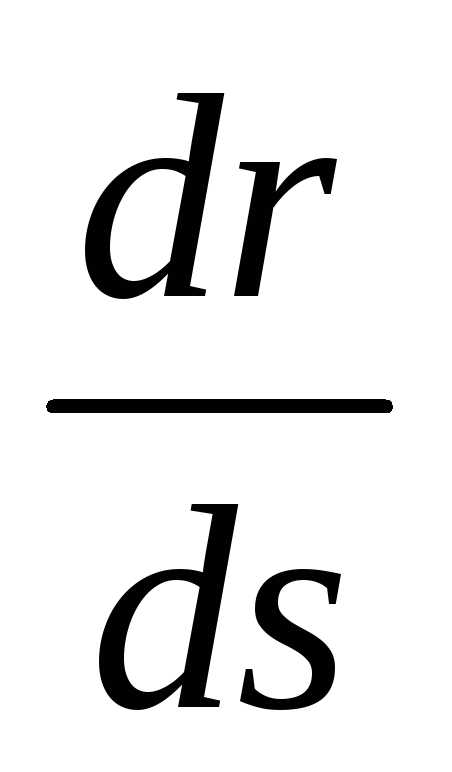 .
.
Сведения из
математики.
Производная 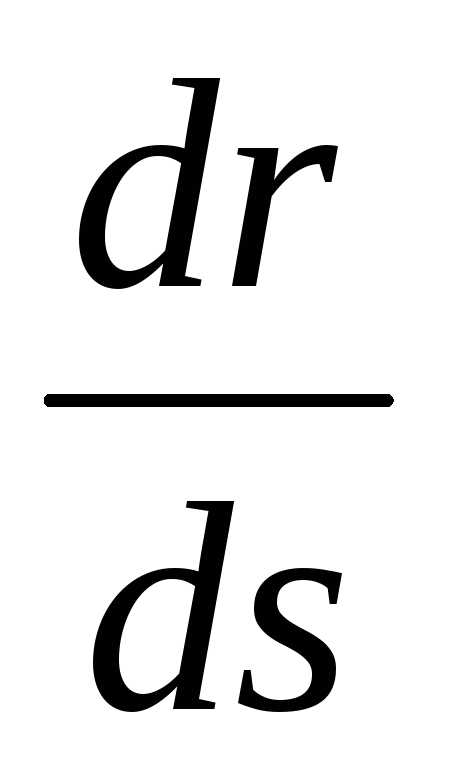 направлена по касательной к годографу
направлена по касательной к годографу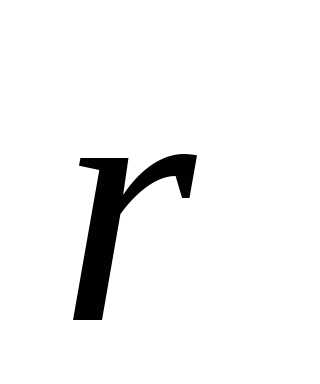 в сторону возрастания дугиS.
С другой стороны, численная величина
производной
в сторону возрастания дугиS.
С другой стороны, численная величина
производной 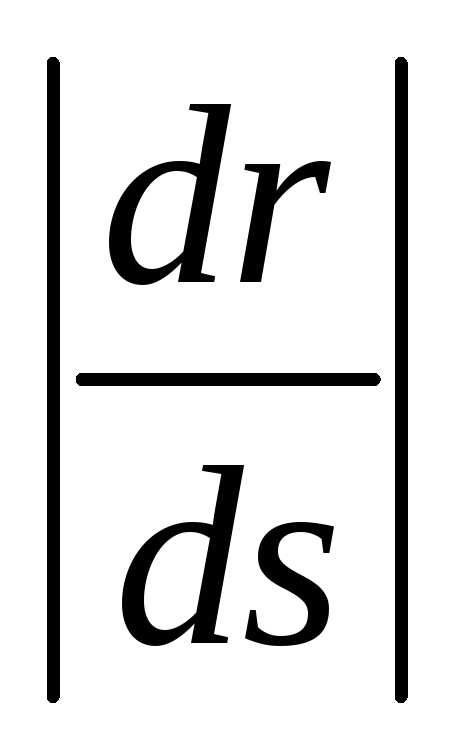 равна
единице, т. к.
равна
единице, т. к.  (хорда
(хорда и дуга
и дуга при
при равны по величине (рис. 1.13)).
равны по величине (рис. 1.13)).
Таким образом, векторная
производная 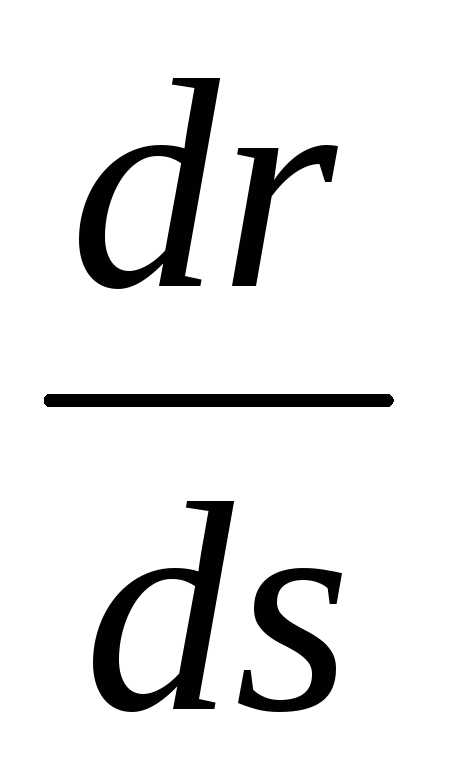 представляет собой единичный вектор
касательной
представляет собой единичный вектор
касательной 
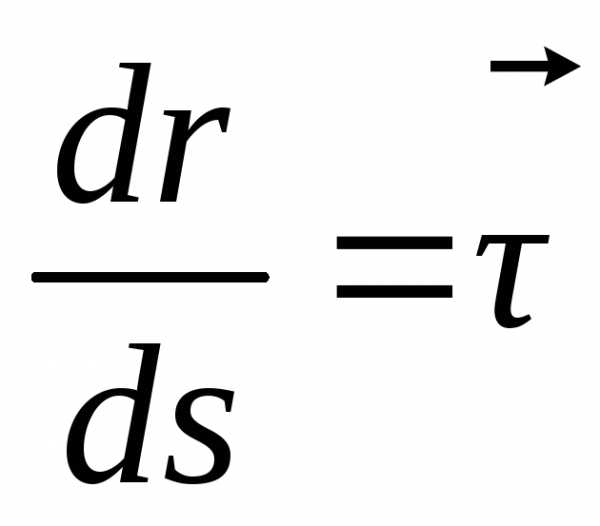 . (1.17)
. (1.17)
С учетом формулы (1.17), формула (1.16) принимает вид
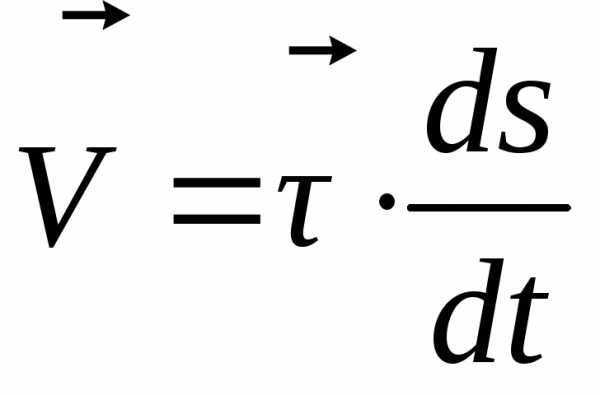 . (1.18)
. (1.18)
Вектор
скорости равен произведению единичного
вектора касательной где |
Проекция вектора
скорости на касательную 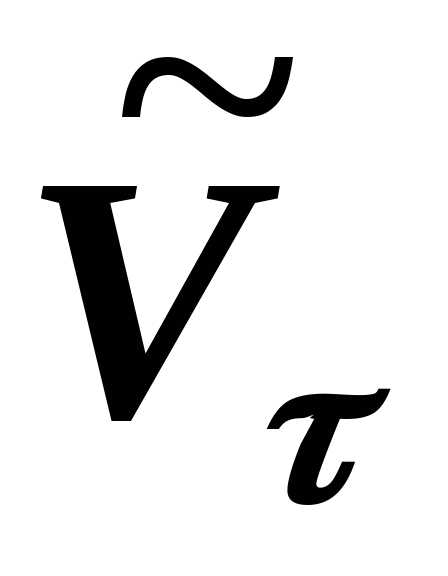 равна производной по времени от дуговой
координаты. На
нормаль и бинормаль проекции вектора
скорости равны нулю:
.
равна производной по времени от дуговой
координаты. На
нормаль и бинормаль проекции вектора
скорости равны нулю:
.
Модуль вектора скорости при естественном способе изучения движения точки равен
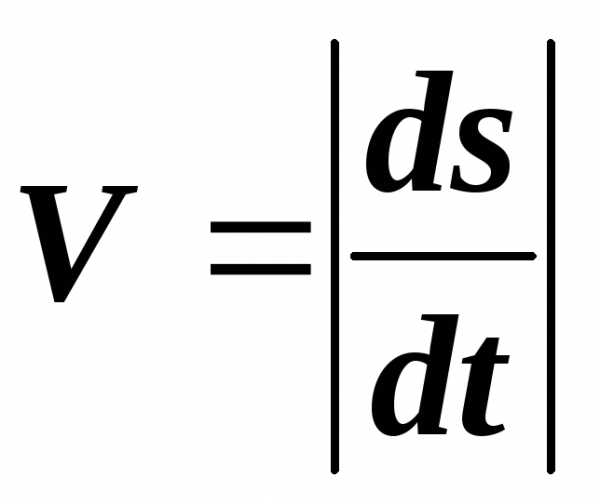 . (1.21)
. (1.21)
Вспомнив, что вектор ускорения есть производная по времени от вектора скорости, получим, согласно формулам (1.8) и (1.19), следующее:
. (1.22)
От вектора  мы берем производную, т. к. этот вектор
при движении точки по криволинейной
траектории меняет свое направление,
оставаясь единичным по модулю, т. е.
вектор
мы берем производную, т. к. этот вектор
при движении точки по криволинейной
траектории меняет свое направление,
оставаясь единичным по модулю, т. е.
вектор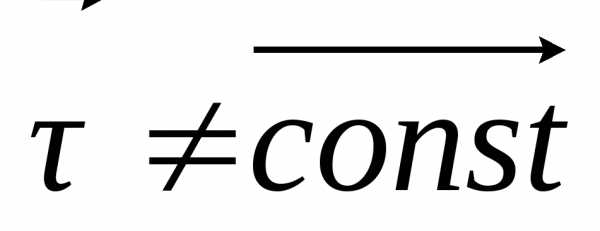 .
.
Учитывая,
что нам известна дуговая координата
как функция времени S (t),
введем в формулу 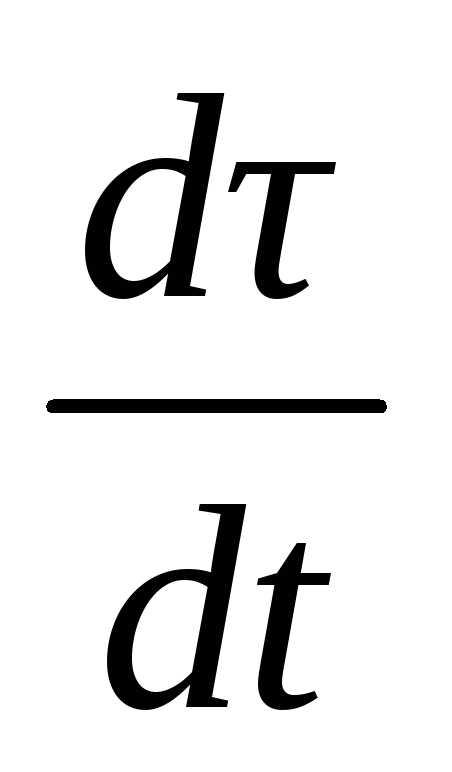 промежуточную переменнуюS,
т. е.
промежуточную переменнуюS,
т. е.
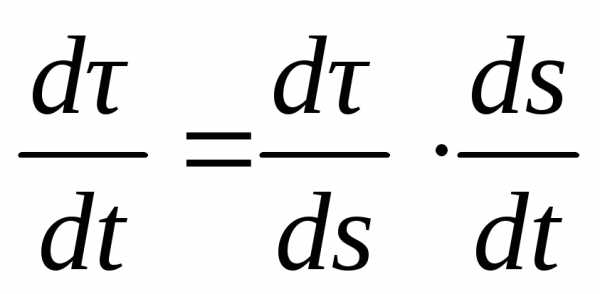 . (1.23)
. (1.23)
Сведения из
математики.
В математике производная  обозначается вектором
обозначается вектором ,
который называетсявектором
кривизны.
Направлен этот вектор по главной нормали
и равняется
,
который называетсявектором
кривизны.
Направлен этот вектор по главной нормали
и равняется
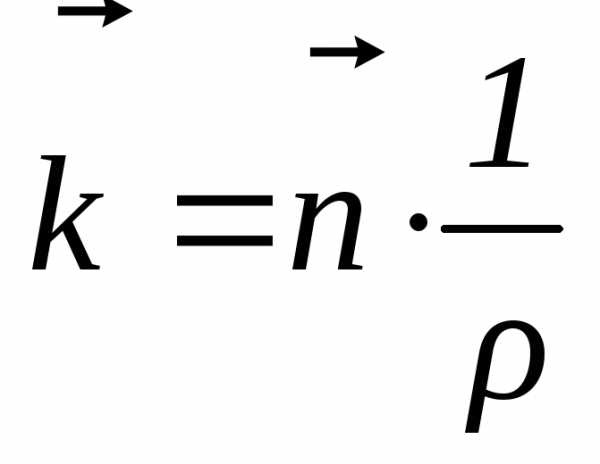 , (1.24)
, (1.24)
где ρ – радиус кривизны кривой.
Покажем несколько радиусов кривизны на рисунке 1.14, помня о том, что для этого нужно в каждой точке кривой М провести окружность, касающуюся этой точки и двух ее ближайших точек М1 и М2. Радиус этой окружности и будет радиусом кривизны в точке М.
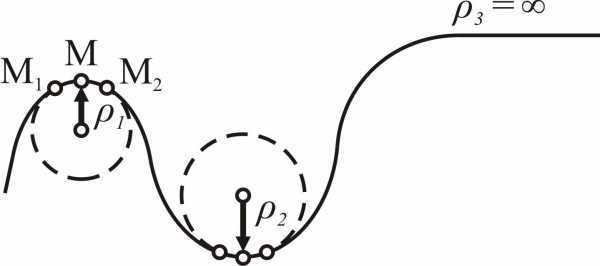
Рисунок 1.14
Учитывая формулы (1.20) и (1.24), вместо (1.23) имеем
. (1.25)
Формула (1.22) с учетом (1.25) имеет вид
. (1.26)
Ускорение точки равно геометрической сумме двух слагаемых: а) вектора касательного ускорения б) вектора нормального ускорения |
Скалярные сомножители
при ортах 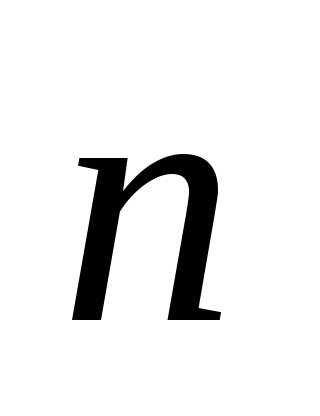 и
и в формулах (1.27) и (1.28) определяютпроекции
ускорения на касательную и нормаль:
в формулах (1.27) и (1.28) определяютпроекции
ускорения на касательную и нормаль:
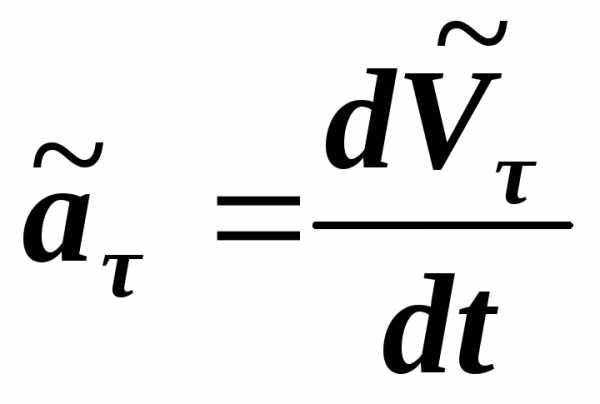 ,
, 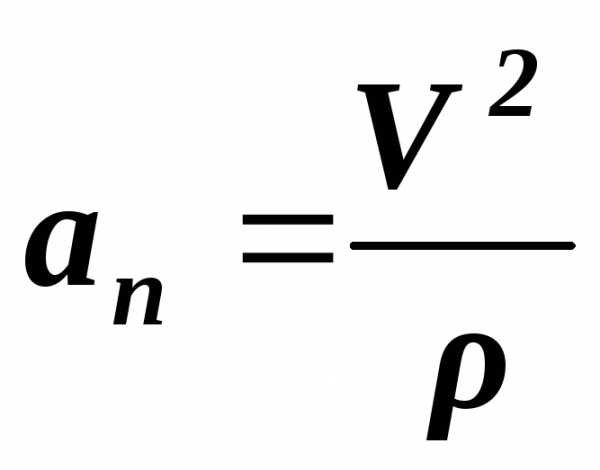 (1.29)
(1.29)
Так как орты  и
и взаимно перпендикулярны, то модуль
полного ускорения точки определяется
по теореме Пифагора (рис. 1.15, 1.16).
взаимно перпендикулярны, то модуль
полного ускорения точки определяется
по теореме Пифагора (рис. 1.15, 1.16).
. (1.30)
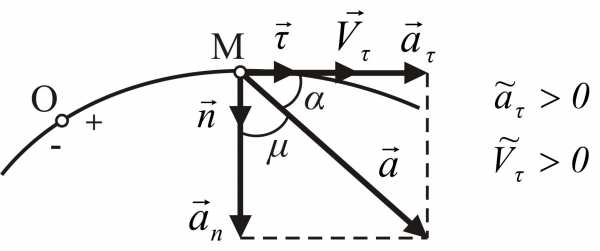
Рисунок 1.15

Рисунок 1.16
Примечание. Имея проекции ускорения на естественные оси координат, можно ответить на вопрос, как движется точка: равномерно, равнопеременно или с переменным ускорением.
Для этого выясним физический
смысл 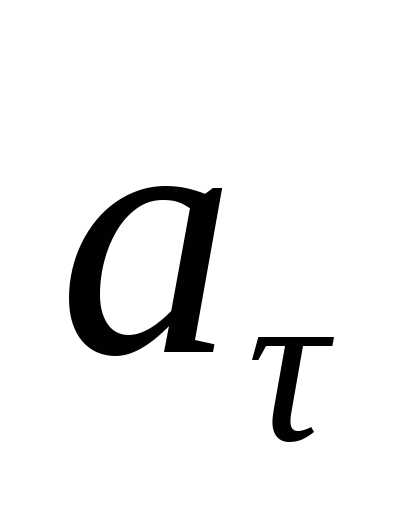 и
и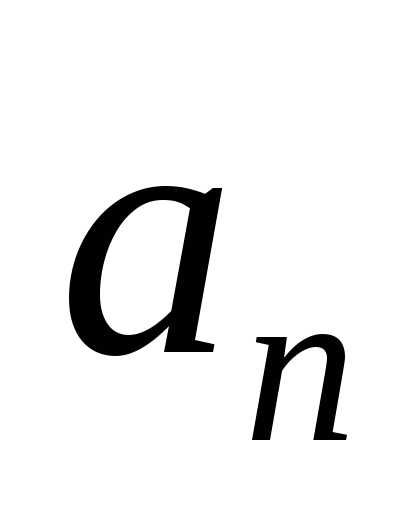 ,
рассмотрев два частных случая движения
точки.
,
рассмотрев два частных случая движения
точки.
П Рисунок 1.17 Вопрос.
Из двух ускорений Ответ.
Нормальное ускорение, его величина | Второй случай. Точка движется по прямой так, что ее величина скорости со временем меняется. Рисунок 1.18 Вопрос.
Какое из двух ускорений Ответ. Нормальное ускорение, так как радиус кривизны траектории равен бесконечности. |
На основании этих примеров сделаем выводы о том, что характеризуют касательное и нормальное ускорения:
Нормальное ускорение характеризует изменение вектора скорости по направлению (рис. 1.17). Касательное ускорение характеризует изменение модуля вектора скорости (рис. 1.18). |
Проекция нормального
ускорения на нормаль 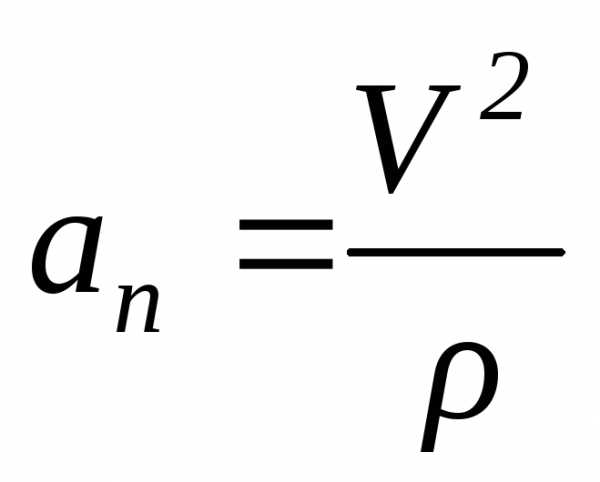 всегда положительная величина, т. е.вектор
всегда положительная величина, т. е.вектор 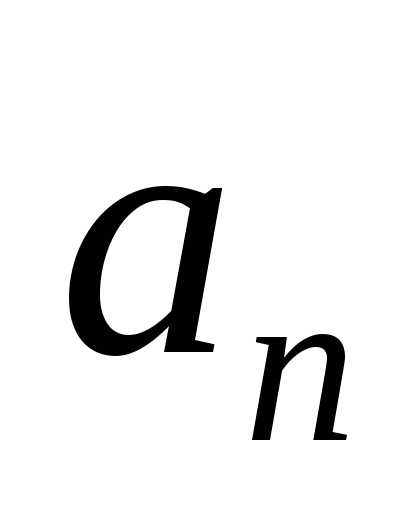 всегда направлен в сторону вогнутости
траектории.
всегда направлен в сторону вогнутости
траектории.
Алгебраическая
величина проекции ускорения на касательную
может как положительной 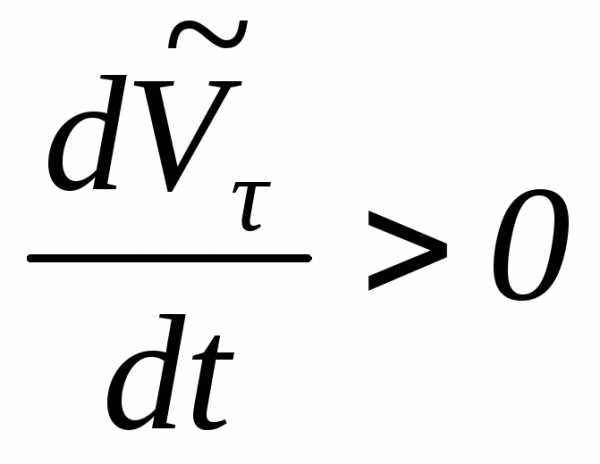 (рис. 1.15), так и отрицательной
(рис. 1.15), так и отрицательной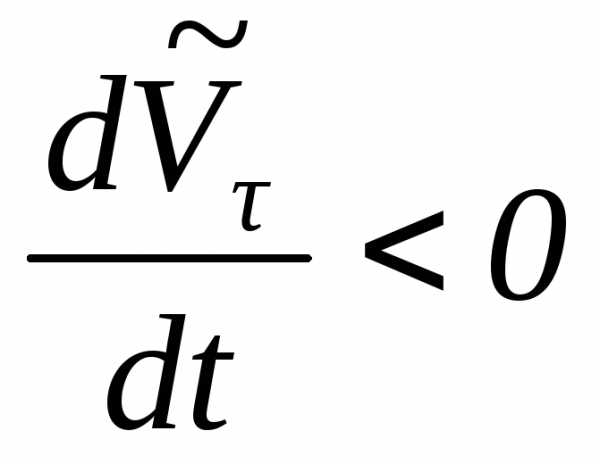 (рис. 1.16).
(рис. 1.16).
Вектор  может совпадать с вектором скорости
может совпадать с вектором скорости  (рис.
1.15),
а может и не совпадать с ним (рис.
1.16).
(рис.
1.15),
а может и не совпадать с ним (рис.
1.16).
Выводы из рисунков 1.15 и 1.16:
1) вектор ускорения точки находится в соприкасающейся плоскости; проекция ускорения на бинормаль равна нулю, т. е. ab = 0;
2) угол μ, который составляет вектор ускорения с радиусом кривизны траектории, определяется формулой
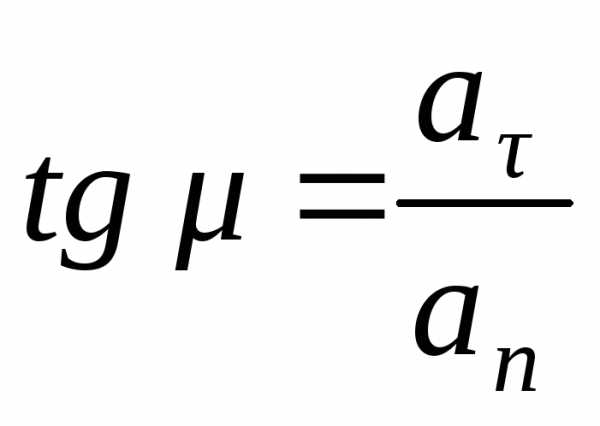 ; (1.31)
; (1.31)
3) по
знаку тангенса угла α в течении некоторого промежутка времени
можно судить о том, движется точка по
кривой ускоренно (если 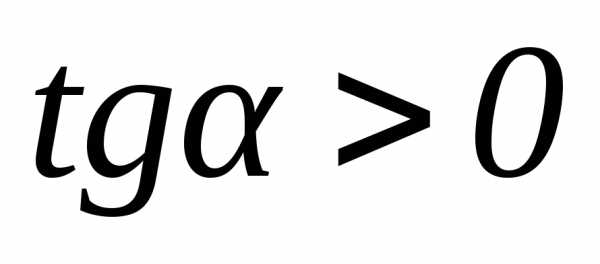 ,
уголα – острый), или замедленно (если
,
уголα – острый), или замедленно (если 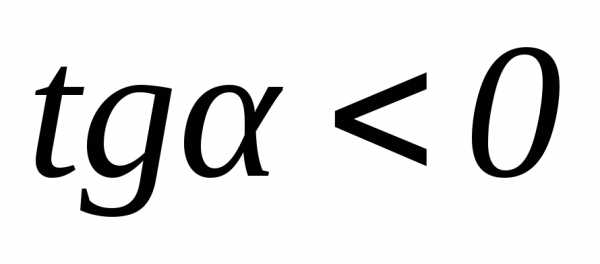 ,
уголα – тупой). Если угол α = 90°, точка не имеет касательного
ускорения, т. е. движется равномерно.
,
уголα – тупой). Если угол α = 90°, точка не имеет касательного
ускорения, т. е. движется равномерно.
studfiles.net
Скорость и ускорение точек тела. Формула Ривальса
Выражение для скорости точки тела в случае его сферического движения имеет вид формулы Эйлера:
(3.32)
Модуль скорости точки тела где h ¾ кратчайшее расстояние от рассматриваемой точки до мгновенной оси вращения (рис.3,12). Таким образом, как и при вращении вокруг неподвижной оси, при сферическом движении вокруг неподвижной точки скорости точек Рис.3.12тела в данный момент времени пропорциональны h.
Вектор скорости точки тела перпендикулярен плоскости, в которой лежат векторы и (заштрихованная плоскость на рис.3.12), т.е. перпендикулярен h и направлен по касательной к мгновенной траектории точки в сторону угловой скорости тела, вращающегося вокруг мгновенной оси.
Если в данный момент времени скорость точки тела равна , то ее ускорение определяется формулой
С учетом (3.32) можно записать,
Поскольку то
(3.33)
 Полученное соотношение называют формулой Ривальса. Ускорение есть геометрическая сумма двух составляющих. ¾вращательное ускорение; ¾осе
Полученное соотношение называют формулой Ривальса. Ускорение есть геометрическая сумма двух составляющих. ¾вращательное ускорение; ¾осе
стремительное ускорение.
Таким образом, (3.34)
Вектор вращательного ускорения
направлен перпендикулярно к плоскости, в которой лежат векторы и (заштрихованная плоскость на рис.3.13), так,что с конца его по Рис.3.13ворот от первого ко второму кажется против хода часовой стрелки. Модуль вектора равен
, (3.35)
где h1¾ кратчайшее расстояние от точки до линии действия вектора углового ускорения в данный момент времени (см. рис.3.13).
Вектор осестремительного ускорения (рис.3.13) перпендикулярен к плоскости, в которой лежат векторы и , и направлен от точки М по перпендикуляру, проведенному из нее на мгновенную ось вращения тела. Модуль вектора , учитывая (3.32) и то, что , равен
(3.36)
Ускорение точки тела, вращающегося вокруг неподвижной точки, равно геометрической сумме векторов вращательного и осестремительного ускорений.
Модуль ускорения равен
(3.37)
Следует отметить, что формула Ривальса (3.33) аналогична формуле ускорения точки тела, вращающегося вокруг неподвижной оси. Но там векторы в отличие от формулы Ривальса.
В о п р о с ы для с а м о к о н т р о л я
1. Дайте определение вращательному движению твердого тела вокруг неподвижной точки.
2. . Какими параметрами определяется положение твердого тела, одна из точек которого неподвижна?
3. Какие параметры (так называемые корабельные углы), предложены Крыловым А.Н для определения положения корабельных носителей на волнении?
4. Что принято за начало неподвижной системы координат,
относительно которой определяется положение (движение) корабельного носителя и связанной с ним подвижной системы координат (рис.3.1) и (рис.3.1,б)?
5. Формулы преобразования координат от связанной с кораблем системы координат к неподвижной системе координат.
6. Поворотные матрицы. Как определяется их структура?
7. В каких случаях рекомендуется использование углов Эйлера?
8. Какие параметры приняты за углы Эйлера. Какие оси называются осями прецессии, нутации, ротации (собственного вращения)?
9, Почему ось нутации называется линией узлов или замечательной осью?
10. Что называют мгновенной осью вращения твердого тела с одной неподвижной точкой и каковы уравнения мгновенной оси в неподвижной и подвижной системах осей декартовых координат?
11. Каково уравнение мгновенной угловой скорости , выраженное как геометрическая сумма трех составляющих ¾угловых скоростей прецессии, нутации, ротации (и линии их действия)?
12. Как определяется модуль и направление углового ускорения тела при сферическом движении?
13. Почему направления векторов углового ускорения и угловой скорости тела при сферическом движении не совпадают?
14. Как определяются скорости точек тела при сферическом движении?
15. Какие модули и направления имеют составляющие ускорения точки тела при сферическом движении?
16. Почему направления векторов скорости точки и ее вращательного ускорения при сферическом движении тела не совпадают?
17. Какой частный случай вращения твердого тела , имеющего одну неподвижную точку, называется регулярной прецессией?
Г л а в а 4
РАСЧЕТНАЯ РАБОТА № 1 –
stydopedia.ru
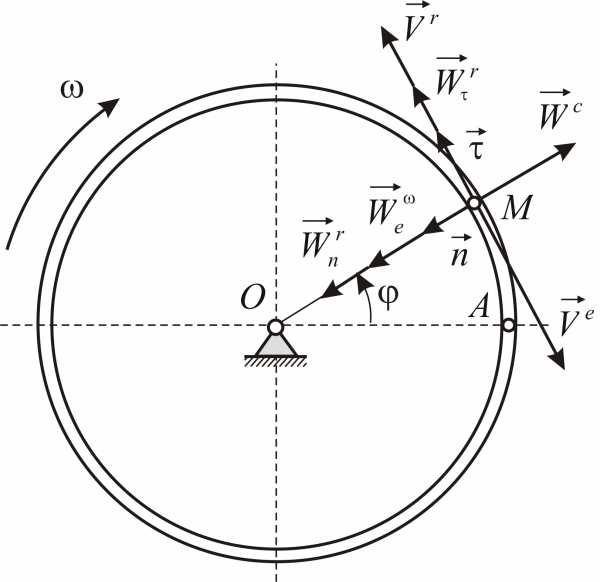
Сложное движение точки Теорема Кориолиса
Здесь мы покажем, что при сложном движении, абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
,
где – кориолисово ускорение.
Пример применения изложенной ниже теории приводится на странице “Сложное движение точки. Пример решения задачи”.
Сложное (составное) движение точки
Часто встречаются случаи, когда точка совершает известное движение относительно некоторого твердого тела. А это тело, в свою очередь, движется относительно неподвижной системы координат. Причем движение точки относительно тела и закон движения тела относительно неподвижной системы координат известны или заданы. Требуется найти кинематические величины (скорость и ускорение) точки относительно неподвижной системы координат.
Такое движение точки называется сложным или составным.
Сложное или составное движение точки – это движение в подвижной системе координат. То есть движение точки описывается в системе координат, которая сама совершает движение относительно неподвижной системы координат.
Далее, для ясности изложения, будем считать, что подвижная система координат жестко связана с некоторым твердым телом. Мы будем рассматривать движение точки относительно тела (относительное движение) и движение тела относительно неподвижной системы координат (переносное движение).
Относительное движение точки при сложном движении – это движение точки относительно тела (подвижной системы координат) считая, что тело покоится.
Переносное движение точки при сложном движении – это движение точки, жестко связанной телом, вызванное движением тела.
Абсолютное движение точки при сложном движении – это движение точки относительно неподвижной системы координат, вызванное движением тела и движением точки относительно тела.
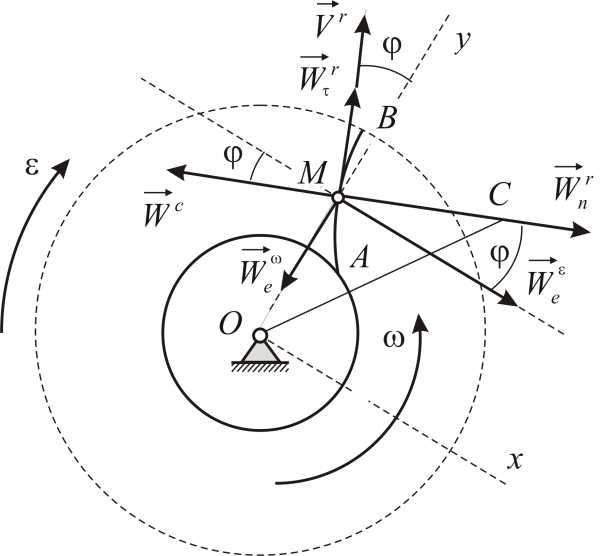
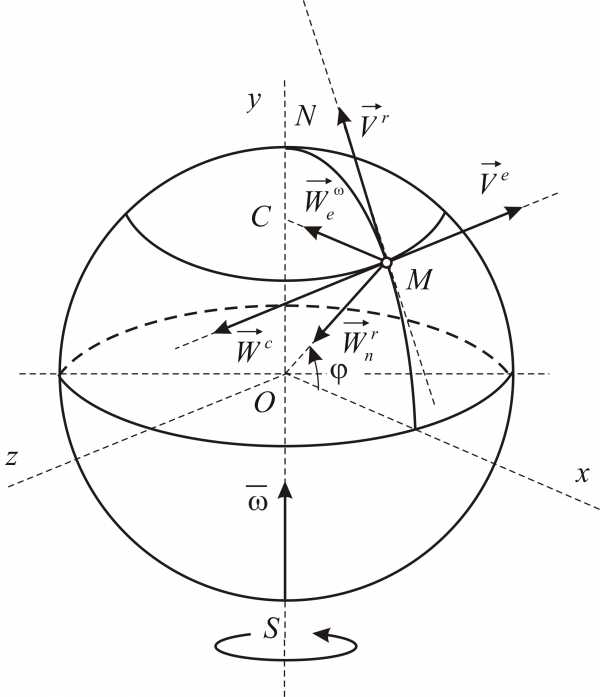
Сложное движение. Точка M движется относительно движущегося тела.
Пусть Oxyz – неподвижная система координат, On xo yo zo – подвижная система координат, жестко связанная с телом. Пусть – единичные векторы (орты), направленные вдоль осей xo , yo , zo подвижной системы координат. Тогда радиус-вектор точки M в неподвижной системе определяется по формуле:
(1) ,
где – радиус-вектор точки On – начала подвижной системы координат, связанной с телом.
Относительная скорость и ускорение
При относительном движении изменяются координаты xo , yo , zo точки относительно тела. А векторы являются постоянными, не зависящими от времени. Дифференцируя (1) по времени, считая постоянными, получаем формулы для относительной скорости и ускорения:
(2) ;
(3) .
Относительная скорость точки при сложном движении – это скорость точки при неподвижном положении тела (подвижной системы координат), вызванная движением точки относительно тела.
Относительное ускорение точки при сложном движении – это ускорение точки при неподвижном положении тела, вызванное движением точки относительно тела.
Переносная скорость и ускорение
При переносном движении изменяются векторы , определяющие положение тела. Относительные координаты точки xo , yo , zo являются постоянными. Дифференцируя (1) по времени, считая xo , yo , zo постоянными, получаем формулы для переносной скорости и ускорения:
(4) ;
(5) .
Переносная скорость точки при сложном движении – это скорость точки, жестко связанной с телом, вызванная движением тела.
Переносное ускорение точки при сложном движении – это ускорение точки, жестко связанной с телом, вызванное движением тела.
Производные по времени от – это скорость и ускорение начала подвижной системы координат On : ; .
Найдем формулы для производных по времени от векторов . Для этого возьмем две произвольные точки твердого тела A и B. Их скорости связаны соотношением:
(см. страницу “Скорость и ускорение точек твердого тела”). Рассмотрим вектор , проведенный из точки A в точку B. Тогда
.
Дифференцируем по времени и применяем предыдущую формулу:
.
Итак, мы нашли формулу для производной по времени от вектора, соединяющего две точки тела:
.
Поскольку векторы жестко связаны с телом, то их производные по времени определяются по этой формуле:
(6) , , .
Подставляем в (4):
.
Таким образом, выражение (4) приводит к формуле для скорости точек твердого тела.
Выполняя подобные преобразования над формулой (5), получим формулу для ускорения точек твердого тела:
,
где – угловое ускорение тела.
Абсолютная скорость и ускорение
При абсолютном движении изменяются как векторы , определяющие положение тела, так и относительные координаты точки xo , yo , zo .
Абсолютная скорость точки при сложном движении – это скорость точки в неподвижной системе координат.
Абсолютное ускорение точки при сложном движении – это ускорение точки в неподвижной системе координат.
Теорема о сложении скоростей
При составном движении абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Доказательство
Дифференцируем (1) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (2) и (4).
(1) ;
(7)
.
Теорема Кориолиса о сложении ускорений
При составном движении абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
,
где
– кориолисово ускорение.
Доказательство
Дифференцируем (7) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (3) и (5).
(7) .
.
В последнем члене применим (6) и (2).
.
Тогда
.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Скорость и ускорение точек твердого тела
Скорость и ускорение точки твердого тела с радиус вектором определяются по формулам:
;
.
где – угловая скорость вращения, – угловое ускорение. Они равны для всех точек тела и могут изменяться со временем t.
и – скорость и ускорение произвольным образом выбранной точки A с радиус вектором . Такую точку часто называют полюсом.
Здесь и далее, произведения векторов в квадратных скобках означают векторные произведения.
Далее мы приводим вывод этих формул исходя из того, что при движении твердого тела, расстояние между двумя любыми его точками остается постоянным.
Вывод формулы для скорости
Выберем прямоугольную неподвижную систему координат Oxyz. Возьмем две произвольные точки твердого тела A и B. Пусть (xA, yA, zA) и (xB, yB, zB) – координаты этих точек. При движении твердого тела они являются функциями от времени t. Их производные по времени t являются проекциями скоростей точек:
, .
Воспользуемся тем, что при движении твердого тела, расстояние |AB| между точками остается постоянным, то есть не изменяется со временем t. Также постоянным является квадрат расстояния
.
Продифференцируем это уравнение по времени t, применяя правило дифференцирования сложной функции.
Сократим на 2.
(1)
Введем векторы
,
.
Тогда уравнение (1) можно представить в виде скалярного произведения векторов:
(2) .
Отсюда следует, что вектор перпендикулярен вектору . Воспользуемся свойством векторного произведения. Тогда можно представить в виде:
(3) .
где – некоторый вектор, который мы вводим только для того, чтобы автоматически выполнялось условие (2).
Запишем (3) в виде:
(4) ,
Теперь займемся изучением свойств вектора . Для этого составим уравнение, которое не содержит скоростей точек. Возьмем три произвольные точки твердого тела A, B и C. Запишем для каждой пары этих точек уравнение (4):
;
;
.
Сложим эти уравнения:
.
Сокращаем сумму скоростей в левой и правой части. В результате получаем векторное уравнение, содержащее только исследуемые векторы :
(5) .
Легко заметить, что уравнение (5) имеет решение:
,
где – какой-то вектор, имеющий равное значение для любых пар точек твердого тела. Тогда уравнение (4) для скоростей точек тела примет вид:
(6) .
Теперь рассмотрим уравнение (5) с математической точки зрения. Если записать это векторное уравнение по компонентам на оси координат x, y, z, то векторное уравнение (5) является линейной системой, состоящей из 3-ех уравнений с 9-ю переменными:
ωBAx , ωBAy , ωBAz , ωCBx , ωCBy , ωCBz , ωACx , ωACy , ωACz .
Если уравнения системы (5) линейно не зависимы, то их общее решение содержит 9 – 3 = 6 произвольных постоянных. Поэтому мы нашли не все решения. Существуют еще какие-то. Чтобы их найти замечаем, что найденное нами решение полностью определяет вектор скорости . Поэтому дополнительные решения не должны приводить к изменению скорости. Заметим, что векторное произведение двух равных векторов равно нулю. Тогда, если в (6) к вектору прибавить член, пропорциональный , то скорость не изменится:
.
Тогда общее решение системы (5) имеет вид:
;
;
,
где CBA, CCB, CAC – постоянные.
Выпишем общее решение системы (5) в явном виде.
ωBAx = ωx + CBA(xB – xA)
ωBAy = ωy + CBA(yB – yA)
ωBAz = ωz + CBA(zB – zA)
ωCBx = ωx + CCB(xC – xB)
ωCBy = ωy + CCB(yC – yB)
ωCBz = ωz + CCB(zC – zB)
ωACx = ωx + CAC(xA – xC)
ωACy = ωy + CAC(yA – yC)
ωACz = ωz + CAC(zA – zC)
Это решение содержит 6 произвольных постоянных:
ωx, ωy, ωz, CBA, CCB, CAC.
Как и должно быть. Таким образом, мы нашли все члены общего решения системы (5).
Физический смысл вектора ω
Как уже указывалось, члены вида не влияют на значения скоростей точек. Поэтому их можно опустить. Тогда скорости точек твердого тела связаны соотношением:
(6) .
– это вектор угловой скорости твердого тела
Выясним физический смысл вектора .
Для этого положим vA = 0. Это всегда можно сделать если выбрать систему отсчета, которая в рассматриваемый момент времени движется относительно неподвижной системы со скоростью . Начало системы отсчета O поместим в точку A. Тогда rA = 0. И формула (6) примет вид:
.
Ось z системы координат направим вдоль вектора .
По свойству векторного произведения, вектор скорости перпендикулярен векторам и . То есть он параллелен плоскости xy. Модуль вектора скорости:
vB = ω rBsin θ = ω |HB|,
где θ – это угол между векторами и ,
|HB| – это длина перпендикуляра, опущенного из точки B на ось z.
Если вектор не меняется со временем, то точка B движется по окружности радиуса |HB| со скоростью
vB = |HB| ω.
То есть ω – это угловая скорость вращения точки B вокруг точки H.
Таким образом, мы приходим к выводу, что – это вектор мгновенной угловой скорости вращения твердого тела.
Скорость точек твердого тела
Итак, мы нашли, что скорость произвольной точки B твердого тела определяется по формуле:
(6) .
Она равна сумме двух членов. Точку A часто называют полюсом. В качестве полюса обычно выбирают неподвижную точку или точку, совершающую движение с известной скоростью. Второй член представляет собой скорость вращения точек тела относительно полюса A.
Поскольку точка B – это произвольная точка, то в формуле (6) можно сделать подстановку . Тогда и скорость точки твердого тела с радиус вектором определяются по формуле:
.
Скорость произвольной точки твердого тела равна сумме скорости поступательного движения полюса A и скорости вращательного движения относительно полюса A.
Ускорение точек твердого тела
Теперь выведем формулу для ускорения точек твердого тела. Ускорение – это производная скорости по времени. Дифференцируем формулу для скорости
,
применяя правила дифференцирования суммы и произведения:
.
Вводим ускорение точки A
;
и угловое ускорение тела
.
Далее замечаем, что
.
Тогда
.
Или
.
То есть вектор ускорения точек твердого тела можно представить в виде суммы трех векторов:
,
где
– ускорение произвольно выбранной точки, которую часто называют полюсом;
– вращательное ускорение;
– осестремительное ускорение.
Если угловая скорость изменяется только по величине и не изменяется по направлению, то векторы угловой скорости и ускорения направлены вдоль одной прямой. Тогда направление вращательного ускорения совпадает или противоположно направлению скорости точки. Если угловая скорость изменяется по направлению, то вращательное ускорение и скорость могут иметь разные направления.
Осестремительное ускорение всегда направлено в сторону мгновенной оси вращения так, что пересекает ее под прямым углом.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
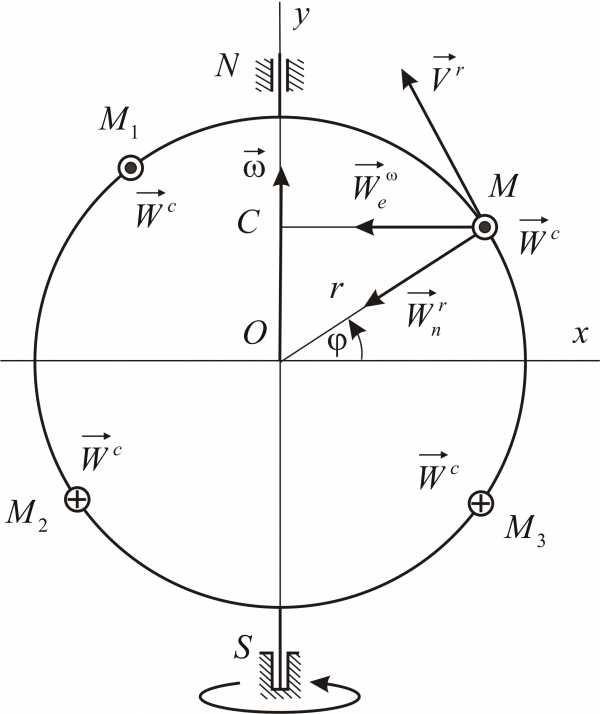
3.2. Вычисление абсолютной скорости и абсолютного ускорения точки
Напомним теорему сложения скоростей при сложном движении точки:
абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей:
Теорема сложения ускорений при сложном движении точки имеет вид:
,
где вектор
называется ускорением Кориолиса.
Таким образом,
абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений.
Пример 3.3
Круглая трубка радиуса 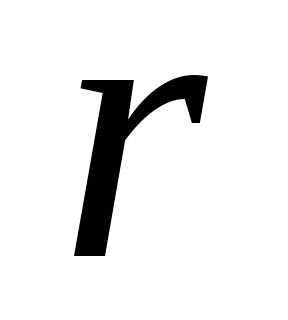 вращается вокруг горизонтальной оси
вращается вокруг горизонтальной оси по часовой стрелке с постоянной угловой
скоростью
по часовой стрелке с постоянной угловой
скоростью .
Внутри трубки около ее точки
.
Внутри трубки около ее точки колеблется шарик
колеблется шарик ,
причем так, что(Рис. 3.5). Определить скорость, касательное
и нормальное ускорения в абсолютном
движении шарика в любой момент времени.
,
причем так, что(Рис. 3.5). Определить скорость, касательное
и нормальное ускорения в абсолютном
движении шарика в любой момент времени.
|
Рис.3.5 |
 с центром в точке
с центром в точке по закону.
Определим закон изменения дуговой
координаты шарика в относительном
движении:
по закону.
Определим закон изменения дуговой
координаты шарика в относительном
движении:Вычислим относительную скорость и относительное ускорение шарика:
Трубка сообщает шарику переносную скорость
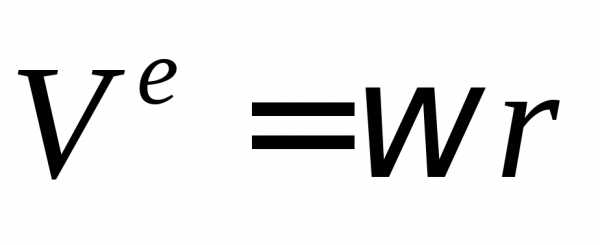
и переносное ускорение
Угол между осью вращения трубки,
вдоль которой направлен вектор ее
угловой скорости, и вектором относительной
скорости шарика равен  ,
так что
,
так что
Для определения направления ускорения Кориолиса удобнее всего воспользоваться правилом Жуковского.
Абсолютная траектория шарика в
данном случае очевидна – это все та же
окружность с центром  радиуса
радиуса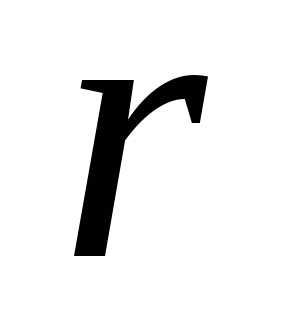 .
Используя теорему сложения скоростей,
получаем:
.
Используя теорему сложения скоростей,
получаем:
Используя теорему Кориолиса (3.12), получаем:
Направления векторов указаны на Рис.
3.5. Ускорение Кориолиса и относительная
скорость представлены на рисунке для
случая 
Пример 3.4
Лопатка  рабочего колеса турбины, вращающегося
против хода часовой стрелки замедленно
с угловым ускорением
рабочего колеса турбины, вращающегося
против хода часовой стрелки замедленно
с угловым ускорением ,
имеет радиус кривизны 0.2 м и центр
кривизны в точке
,
имеет радиус кривизны 0.2 м и центр
кривизны в точке ,
причемм. Частица воды
,
причемм. Частица воды ,
отстоящая от оси
,
отстоящая от оси турбины на расстоянии 0.2 м, движется по
лопатке наружу и имеет скорость 0.25 м/с
и касательное ускорение 0.5 м
турбины на расстоянии 0.2 м, движется по
лопатке наружу и имеет скорость 0.25 м/с
и касательное ускорение 0.5 м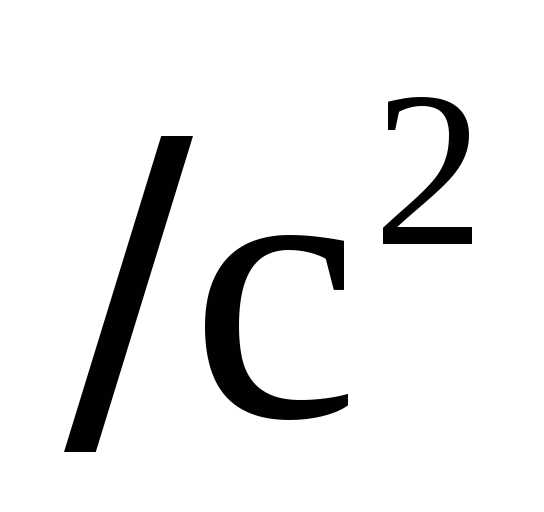 по отношению к лопатке. Определить
абсолютное ускорение частицы
по отношению к лопатке. Определить
абсолютное ускорение частицы в тот момент времени, когда угловая
скорость турбины равна 2 рад/с.
в тот момент времени, когда угловая
скорость турбины равна 2 рад/с.
Подвижную систему координат свяжем
с рабочим колесом турбины (Рис. 3.6).
Относительной траекторией частицы воды
является кривая  – лопатка турбины. Определим нормальное
ускорение точки
– лопатка турбины. Определим нормальное
ускорение точки в относительном движении
в относительном движении
Точка  турбины описывает окружность с центром
турбины описывает окружность с центром радиуса
радиуса .
Определим переносное ускорение точки:
.
Определим переносное ускорение точки:
Направление ускорения Кориолиса определяем по правилу Жуковского. Модуль ускорения Кориолиса равен
Используя теорему Кориолиса, найдем
проекции абсолютного ускорения частицы  на оси подвижной системы координат
(Рис. 3.6):
на оси подвижной системы координат
(Рис. 3.6):
|
| |
Рис. 3.6 | Рис. 3.7 |
Остается определить  и
и .
Для этого используем теорему косинусов
(Рис. 3.7):
.
Для этого используем теорему косинусов
(Рис. 3.7):
Отсюда
Таким образом,
Окончательно получаем:
Пример 3.5
Диск радиуса 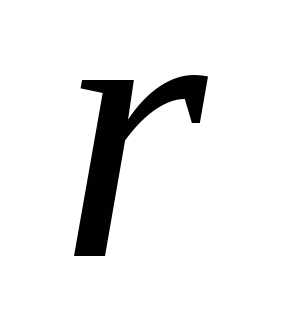 вращается вокруг неподвижной оси
вращается вокруг неподвижной оси с постоянной угловой скоростью
с постоянной угловой скоростью .
По ободу диска движется точка
.
По ободу диска движется точка ,
имея относительно диска постоянную по
модулю скорость
,
имея относительно диска постоянную по
модулю скорость .
Определить абсолютную скорость и
абсолютное ускорение точки
.
Определить абсолютную скорость и
абсолютное ускорение точки .
.
Подвижную систему отсчета связываем
с диском (Рис. 3.8). По отношению к диску,
т.е. в относительном движении, точка  движется равномерно со скоростью
движется равномерно со скоростью ,
описывая окружность радиуса
,
описывая окружность радиуса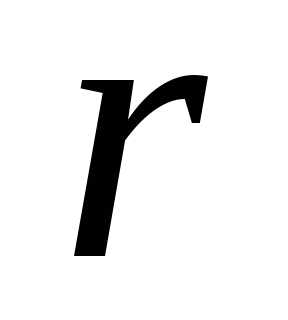 с центром в точке
с центром в точке .
Определяем относительное ускорение
точки:
.
Определяем относительное ускорение
точки:
Рассмотрим переносное движение –
его совершает диск. Точка  диска описывает окружность с центром
диска описывает окружность с центром ,
плоскость которой параллельна координатной
плоскости
,
плоскость которой параллельна координатной
плоскости .
Переносная скорость
.
Переносная скорость
направлена по касательной к этой
окружности в сторону вращения диска,
т.е. перпендикулярно плоскости диска в
отрицательном направлении координатной
оси  .
Поскольку вращение диска по условию
равномерное, отличным от нуля оказывается
только осестремительное ускорение:
.
Поскольку вращение диска по условию
равномерное, отличным от нуля оказывается
только осестремительное ускорение:
Вектор ускорения Кориолиса точки  направлен перпендикулярно плоскости
чертежа, в которой расположены векторы
направлен перпендикулярно плоскости
чертежа, в которой расположены векторы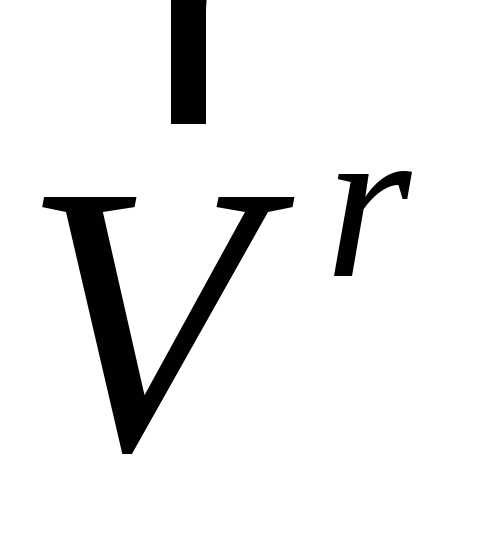 и
и ,
причем, в ту сторону, откуда кратчайшее
совмещение направления вектора
,
причем, в ту сторону, откуда кратчайшее
совмещение направления вектора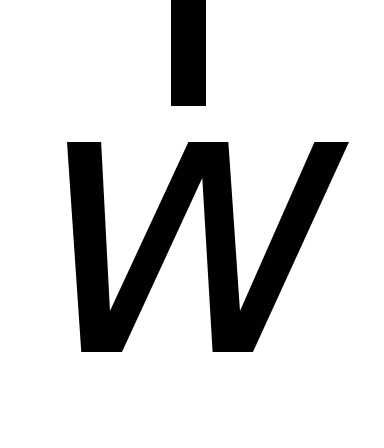 с направлением вектора
с направлением вектора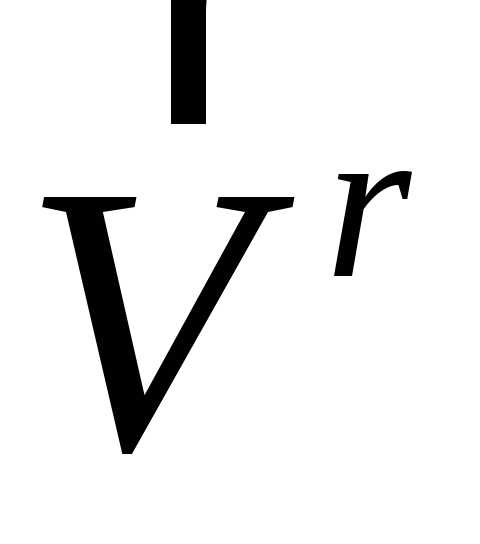 видно против хода часовой стрелки. В
указанном на Рис. 3.9 положении точки
видно против хода часовой стрелки. В
указанном на Рис. 3.9 положении точки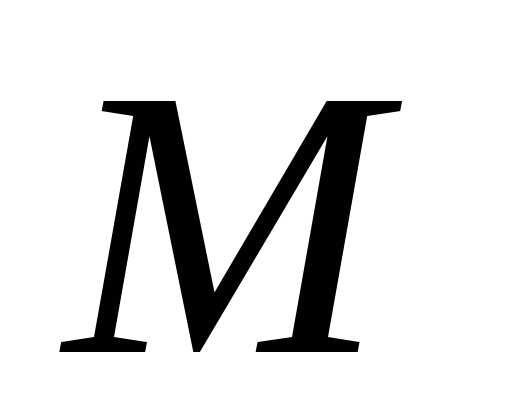 вектор ускорения Кориолиса направлен
на нас, т.е. параллелен координатной
оси
вектор ускорения Кориолиса направлен
на нас, т.е. параллелен координатной
оси в положительную сторону этой оси. На
Рис. 3.9 это направление условно обозначено
острием стрелки, заключенным в кружок.
Модуль ускорения Кориолиса вычисляется
по формуле:
в положительную сторону этой оси. На
Рис. 3.9 это направление условно обозначено
острием стрелки, заключенным в кружок.
Модуль ускорения Кориолиса вычисляется
по формуле:
.
|
| ||
Рис.3.8 | Рис.3.9 | ||
При перемещении точки  по диску направление ускорения Кориолиса
не будет изменяться до тех пор, пока
по диску направление ускорения Кориолиса
не будет изменяться до тех пор, пока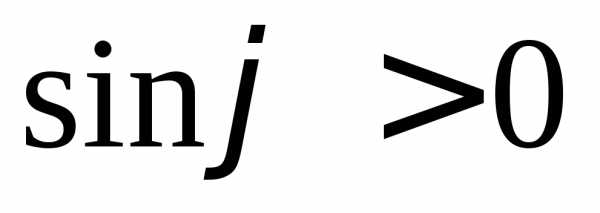 ,
т.е. пока(точка
,
т.е. пока(точка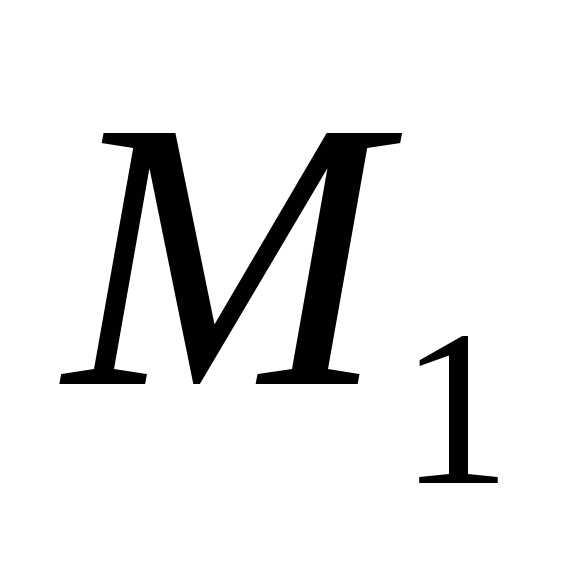 ).
При пересечении точкой
).
При пересечении точкой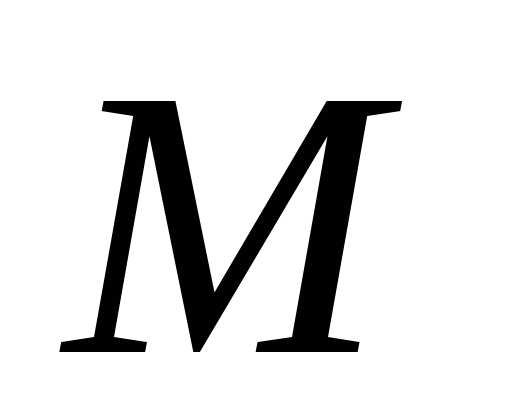 координатной оси
координатной оси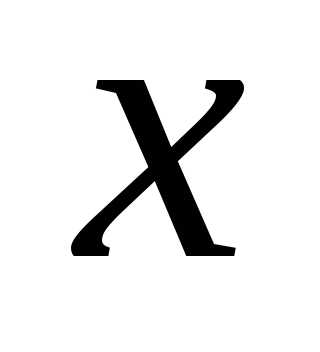 ускорение Кориолиса обращается в нуль.
При движении точки в нижней части диска,
т.е. при,
проекция ускорения Кориолиса на
направление оси
ускорение Кориолиса обращается в нуль.
При движении точки в нижней части диска,
т.е. при,
проекция ускорения Кориолиса на
направление оси становится отрицательной и вектор
становится отрицательной и вектор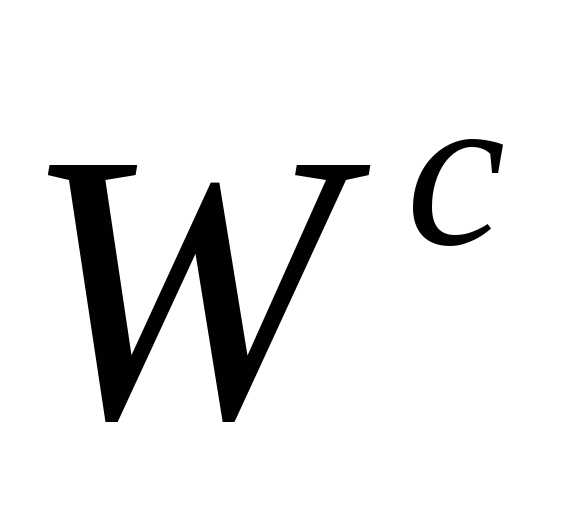 направлен от нас (точки
направлен от нас (точки и
и ).
).
Таким образом,
Используя теорему сложения скоростей
находим проекции вектора абсолютной скорости на оси подвижной системы координат:


Используя теорему Кориолиса
находим проекции абсолютного ускорения точки на оси подвижной системы координат:

Примечание.
Последняя задача позволяет проиллюстрировать некоторые явления, связанные с вращением Земли, в частности, размыв берегов рек. Как видно, вращение Земли приводит к возникновению у частиц воды кориолисова ускорения, направленного перпендикулярно линии берегов. Наличие такого ускорения приводит к тому, что в северном полушарии дополнительно подмывается правый берег, который на прямолинейных участках рек заметно выше левого берега. В южном полушарии более высокий левый берег. Это явление в географии отражено в законе Бэра.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 22.10; 22.14; 22.17; 22.26; 23.1; 23.9; 23.13; 23.18; 23.19; 23.27; 23.29; 23.34; 23.47; 23.48; 23.49; 23.56.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА – теория и практика»: комплекты СР-23;
СР-24; СР-25.
КОНТРОЛЬНЫЕ МЕРОПРИЯТИЯ:
После практического занятия №7(15) проводится тест «МОДУЛЬ КБ».
ЛИТЕРАТУРА:
Антонов В.И., Белов В.А., Егорычев О.О., Степанов Р.Н.//Курс теоретической механики (теория и практика) – М.: Архитектура – С, 2011 г.
Мещерский И.В.//Сборник задач по теоретической механике. – Спб.: Лань, 2010 г.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1
studfiles.net

 на проекцию вектора на касательную
на проекцию вектора на касательную  :
: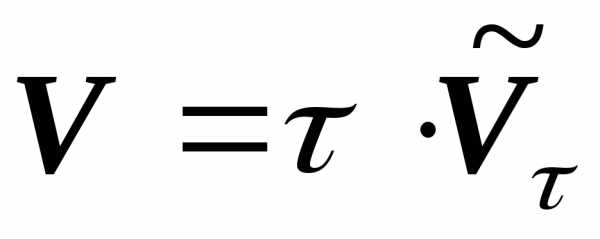 ,
(1.19)
,
(1.19)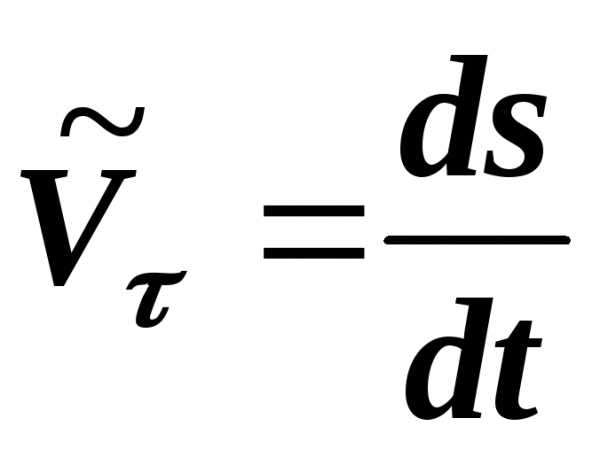 .
(1.20)
.
(1.20) ,
(1.27)
,
(1.27)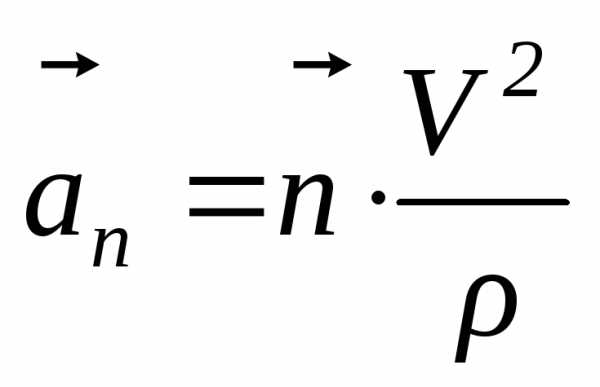 . (1.28)
. (1.28)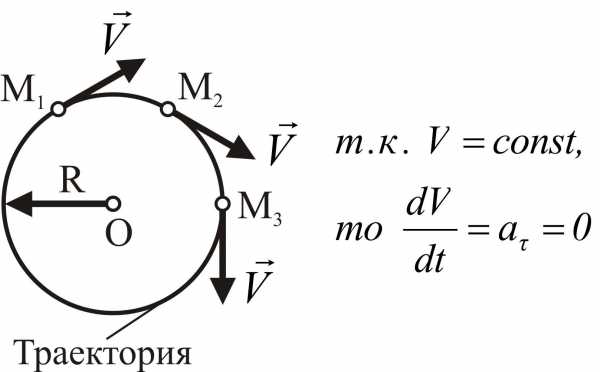 ервый
случай.
Точка движется по окружности радиуса R с постоянной по величине скоростью V (равномерно).
ервый
случай.
Точка движется по окружности радиуса R с постоянной по величине скоростью V (равномерно). и
и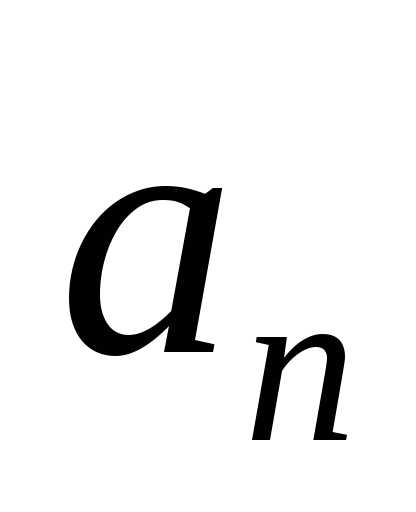 ,
какое ускорение точки не равно нулю?
,
какое ускорение точки не равно нулю? .
. и
и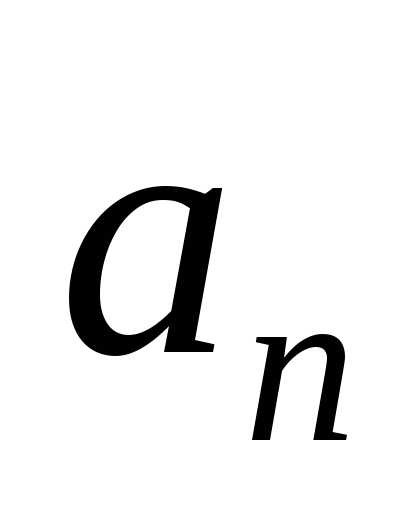 равно
нулю?
равно
нулю?