24.06.201913.12.2018

Ускорение и скорость – Скорость и ускорение. Среднее ускорение, мгновенное ускорение. Тангенциальное и нормальное ускорение. Полное ускорение.

• by alexxlab
• Комментариев к записи Ускорение и скорость – Скорость и ускорение. Среднее ускорение, мгновенное ускорение. Тангенциальное и нормальное ускорение. Полное ускорение. нет
• Советы абитуриенту

Кинематика (скорость, ускорение, путь). Формулы, примеры решения

В прошлой статье мы немножко разобрались с тем, то такое механика  и зачем она нужна. Мы уже знаем, что такое система отсчета,  относительность движения и материальная точка. Что ж, пора двигаться дальше!  Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики  и приведем практический пример решения задачи.

Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад  в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.

Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.

Траектория, радиус-вектор, закон движения тела

Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.

Радиус-вектор – вектор, задающий положение точки в пространстве.

Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат  (или радиус-век

zaochnik.ru

Kvant. Скорость ускорение — PhysBook

Соколов Е. Скорость и ускорение //Квант. — 2011. — № 1. — С. 34

По специальной договоренности с редколлегией и редакцией журнала “Квант”

Для описания состояния движущегося тела в данный момент времени в кинематике вводятся понятия вектора скорости \(~\vec{\upsilon}\) и вектора ускорения \(~\vec{a}\) . А когда есть два вектора, то естественно поставить вопрос об их взаимном расположении. Например, такой: может ли угол между скоростью и ускорением быть равным 37° ?

Вопрос непростой, и в нашем классе его обсуждение превратилось в оживленную дискуссию.

Первым у нас всегда спешит с ответом Саша.

— Конечно, нет, такого быть не может! А вот угол 90° между скоростью и ускорением может быть (рис.1,а). Мы уже встречались с тем, что когда тело движется по окружности с постоянной по модулю скоростью, то у него есть ускорение. Это ускорение всегда направлено перпендикулярно скорости, т.е. к центру окружности, поэтому ему дали специальное название – центростремительное ускорение.

— И не только 90°, – поправила его Яна. – Помните, мы говорили, что при свободном падении ускорение тела всегда направлено вниз (рис.1,б). Поэтому угол между скоростью и ускорением может быть равен 0°.

— А ведь свободное падение это не только движение вниз, – вмешалась Маша. – Свободным падением можно называть любое движение тела под действием только силы тяжести, например в отсутствие сопротивления воздуха. Поэтому даже когда мяч летит вверх, его ускорение, согласно нашему правилу, по-прежнему направлено вниз (рис.1,е). Угол между скоростью и ускорением в этом случае равен 180°.

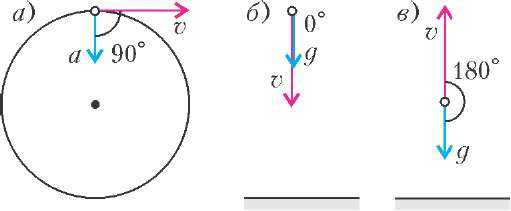
— Вот мы и ответили на ваш вопрос: угол между скоростью и ускорением может принимать три значения, – подытожил разговор Иван.

— Ну что же, вы нашли три возможных угла. Можете отдохнуть и полюбоваться еще одной знакомой вам картинкой (рис.2). Скажу честно – это намек. На рисунке 2 изображена траектория тела, брошенного под углом к горизонту. Такую ситуацию мы не раз обсуждали и говорили, что скорость тела в каждой точке направлена по касательной к траектории, а ускорение все время направлено вниз. Ведь куда бы ни летело тело, оно всегда свободно падает. Нарисуем для нескольких точек траектории векторы скорости и ускорения (рис.3). В верхнее точке А скорость направлена горизонтально, а ускорение направлено вниз. В этой точке угол между скоростью и ускорением равен 90° . Для точки В соответствующий угол острый, а для точки С – тупой. И понятно, что величины этих углов могут быть любыми.

Итак, вот итог наших размышлений: угол между скоростью и ускорением может быть любым.

Это хорошо, что мы нашли правильный ответ, но, к сожалению, жизнь наша от этого только усложнилась. Ведь если бы существовало только три угла, то достаточно было бы выбрать один вариант из трех. Но теперь мы знаем, что ускорение может быть направлено куда угодно, и вариантов стало бесконечно много. Как же быть? Как в задачах правильно рисовать, куда направлено ускорение тела? Сейчас разберемся. Но прежде сделаем общее замечание.

В процессе эволюции человек приобрел способность «видеть» скорость и траекторию. Так, мы хорошо представляем себе, куда полетит брошенный нами снежок, и легко сможем увернуться от летящего в нас снежка. Поэтому вопросы, связанные со скоростью и траекторией, обычно не вызывают сложностей. Но мы не имеем возможности «видеть» ускорение. Вот почему просто так, по наитию, не стоит пытаться его рисовать. Определить, как направлено ускорение в каждом случае, мы можем только с помощью рассуждений, применяя специальные правила. О двух таких правилах мы уже знаем: при равномерном движении тела по окружности ускорение следует направлять к центру окружности (доказывается в кинематике), а при свободном падении – вертикально вниз (доказывается в динамике).

— А есть общее правило для любого движения?

— Да, есть. И его под силу вывести любому первокурснику. Но вы еще не первокурсники, а я очень не люблю рассказывать что-то без доказательств. Давайте поступим так: превратим наше обсуждение в тест на обучаемость. Я честно, хотя и без доказательств, расскажу вам все, что нужно для построения ускорения, и даже открою вам некоторые секреты, а потом вы попытаетесь построить ускорение в десяти простых случаях.

— Согласны. Только разве сложно, зная правила, получить ответ?

— Вот это мы как раз и проверим на опыте. А пока слушайте и задавайте вопросы.

Найти направление ускорения помогают два понятия: нормальная составляющая ускорения и тангенциальная составляющая ускорения. Общее правило заключается в том, что сначала строится каждая из этих составляющих (это несложно сделать), а уже по ним – само ускорение, как показано на рисунке 4.

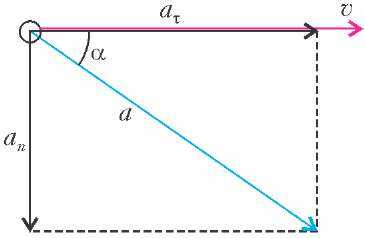
Нормальная составляющая ускорения – это составляющая, перпендикулярная скорости. Величину нормальной составляющей ускорения всегда можно найти по уже знакомой нам формуле

\(~a_n = \dfrac{\upsilon^2}{R}. \)

Эта составляющая перпендикулярна скорости и направлена по радиусу R к центру кривизны траектории. Нормальная составляющая ускорения (второе, уже знакомое нам название этой составляющей – центростремительное ускорение) характеризует быстроту изменения направления скорости.

Тангенциальная, или касательная, составляющая ускорения – это составляющая, направленная параллельно скорости. Она характеризует быстроту изменения скорости по величине и определяется по формуле

\(~a_\tau = \dfrac{\Delta \upsilon}{\Delta t}\)

Направлять тангенциальную составляющую следует либо по направлению скорости, либо против – в зависимости от того, увеличивается скорость или уменьшается.

Определив обе эти составляющие, мы можем с помощью рисунка 4 восстановить само ускорение (иногда говорят «полное ускорение»). При необходимости модуль ускорения и угол между скоростью и ускорением можно вычислить с помощью теоремы Пифагора и понятия арктангенса:

\(~a = \sqrt{a_n^2 + a_\tau^2}, \ \ \ \alpha = \arctan{ \dfrac{a_n}{a_\tau} }. \)

Ну как, понятно?

— Да, вроде все ясно. Сначала рисуем нормальную составляющую ускорения перпендикулярно скорости в направлении к центру кривизны – так же, как мы рисовали центростремительное ускорение. Потом строим вторую составляющую – вдоль или против скорости. И после этого по рисунку 4 находим само ускорение.

— Все правильно. Но прежде чем переходить к тесту, я хочу обратить ваше внимание на очень важные частные случаи. Выполните, пожалуйста, такое упражнение: а) укажите два случая движения тела, в которых нормальная составляющая ускорения обращается в ноль; б) укажите два случая движения тела, в которых тангенциальная составляющая ускорения обращается в ноль. Лучше будет, если вы сами ответите на эти вопросы, но ничего страшного не произойдет, если вы просто прочтете следующие два абзаца.

а) Нормальная составляющая ускорения обращается в ноль тогда, когда обращается в ноль выражение \(~a_n = \dfrac{\upsilon^2}{R}\) . А это может произойти в двух случаях. Первый случай видят все: нормальная составляющая обращается в ноль, если скорость обращается в ноль. Поэтому нормальная составляющая ускорения всегда равна нулю в точках остановки тела.

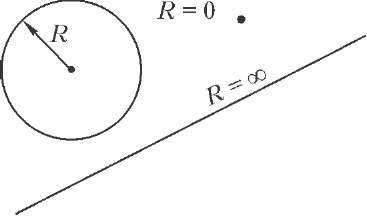
Второй случай увидит лишь тот, кто знает, что общего у прямой, окружности и точки. Оказывается, и точка, и прямая есть частные случаи окружности (рис. 5). Точка – это окружность с радиусом, равным нулю, а прямая – это окружность с радиусом, равным бесконечности. Не верите? Попробуйте нарисовать на компьютере окружность очень большого радиуса. Она практически не будет отличаться от прямой линии. Итак, второй случай, когда нормальная составляющая обращается в ноль, – это случай, когда R = ∞ , т.е. когда тело движется по прямой. При прямолинейном движении нормальной составляющей ускорения нет.

б) Тангенциальная составляющая ускорения обращается в ноль тогда, когда обращается в ноль выражение \(a_\tau = \dfrac{\Delta \upsilon }{\Delta t} = \upsilon ‘ (t)\) А это тоже может произойти в двух случаях. Первый случай – это равномерное движение, когда модуль скорости вообще не изменяется. Второй случай – это моменты времени, когда модуль скорости достигает максимума или минимума и производная от модуля скорости по времени становится равной нулю.

Наш рассказ о кинематическом методе построения ускорения закончен. Теперь попробуйте выполнить приведенный ниже тест. В нем собраны, пожалуй, все возможные случаи построения ускорения. Отметим, что этот тест не так прост, как кажется.

Тест. Для каждого из десяти положений тела, изображенных на рисунке 6, определите, как направлено его ускорение.

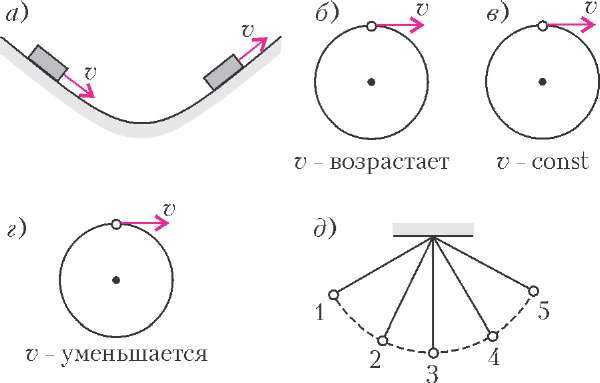
а) Санки скатываются с горки, а затем заезжают на горку.

б )Тело движется по окружности с возрастающей скоростью.

в) Тело движется по окружности с постоянной скоростью.

г) Тело движется по окружности с уменьшающейся скоростью.

д) Математический маятник совершает колебания. Точки 1 и 5 — крайние точки, 2 и 4 — промежуточные, 3 — самая нижняя точка.

В заключение – одно полезное замечание. Наш разговор о направлении ускорения мы вели на языке кинематики. Однако говорить об этом можно и на языке динамики. Иногда (но не всегда) динамические рассуждения могут оказаться проще кинематических. Например, с помощью динамики очень легко ответить на исходный вопрос об угле 37° . Динамика учит, что ускорение порождается силой.

Согласно второму закону Ньютона, \(~\vec{ a } = \dfrac{ \vec{F} }{ m }\) , т.е. куда направлена сила, туда направлено и ускорение. Силу мы можем прикладывать в любом направлении по нашему желанию, поэтому и ускорение, создаваемое этой силой, может иметь любое направление.

Ответы

а) В каждом из двух случаев ускорение совпадает с тангенциальной составляющей ускорения (рис.7, а).

б) Тело движется по окружности, значит, у тела есть нормальная составляющая ускорения, которая направлена к центру окружности. Кроме этого, по условию задачи скорость тела возрастает, следовательно, есть и тангенциальная составляющая ускорения, которая направлена вдоль скорости. Полное ускорение \(\vec{а}\) изображено на рисунке 7, б.

в) См. рис.7, в

г) См. рис.7, г.

д) Прежде всего отметим, что траектория движения математического маятника – это окружность (рис.7, д). Поэтому, там, где скорость тела не равна нулю, есть нормальная составляющая ускорения.

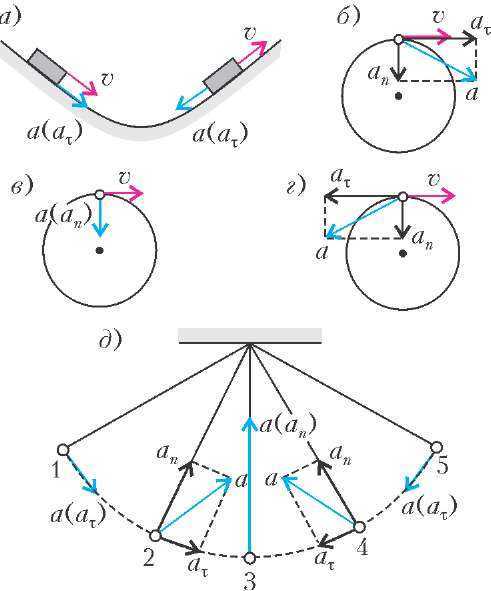
Крайние точки 1 и 5 — это точки поворота. Скорость в этих точках обращается в ноль, поэтому нормальная составляющая ускорения в обеих точках равна нулю. А есть ли в этих точках тангенциальная составляющая? Вот здесь, бывает, ошибаются даже самые сильные школьники. Правильный ответ – да, тангенциальное ускорение в точках остановки есть. Проще всего применить к этим точкам второй метод рассуждений — динамический. В точках 1 и 5 на тело действуют две силы: сила тяжести и сила натяжения нити. Касательная составляющая силы тяжести и создает тангенциальное ускорение.

www.physbook.ru

Скорость, ускорение и сила | Создавая картину Вселенной

Скорость, ускорение и сила

Теория движения Ньютона и математический язык, который он создал для ее выражения, основана на законе инерции. Галилей, как мы уже говорили, сформулировал закон инерции для горизонтального движения по поверхности Земли: если бы Земля была идеально гладкой сферой, то тело, скользящее без трения по ее поверхности, перемещалось бы с постоянной скоростью вдоль дуги большого круга и в конечном итоге вернулось бы в исходную точку, причем для поддержания этого движения к телу не нужно прикладывать никакой силы.

Ньютон осознал, что этот «закон горизонтальной инерции» не столь прост, как казалось Галилею. Тело, скользящее без трения по гладкой поверхности сферической Земли, на самом деле не движется свободно. На него действуют две противоположно направленные силы: сила земного притяжения, направленная к центру Земли, и реакция опоры, обусловленная давлением тела на земную поверхность. Скорость тела в горизонтальном направлении не меняется, поскольку на тело не действует никакая горизонтально направленная сила. Однако если бы на тело не действовало никаких сил вообще, то оно после того, как ему сообщили начальную скорость, продолжало бы двигаться в соответствующем направлении равномерно и прямолинейно.

Данная фраза представляет собой формулировку первого закона Ньютона. Его можно выразить и более кратко: скорость свободной частицы не меняется со временем. Скорость частицы – это вектор, который характеризуется как величиной, так и направлением. Вектор можно изобразить в виде стрелки, длина которой соответствует мгновенной скорости частицы, а направление параллельно направлению мгновенной скорости частицы в интересующий нас момент времени. Вектор мгновенной скорости частицы всегда направлен по касательной к ее траектории, и если траектория криволинейна, то направление движения непрерывно изменяется. Из первого закона Ньютона следует, что свободная частица не может двигаться по криволинейной траектории – криволинейное движение возможно лишь под действием силы.

Каким образом сила изменяет скорость частицы? Теория движения снарядов, разработанная Галилеем, дает ответ на этот вопрос. Галилей утверждал, что движение тела в вертикальном направлении не зависит от движения в горизонтальном направлении. Вертикальное движение снаряда – равноускоренное, а перемещение вдоль поверхности Земли происходит равномерно.

Ньютон понял, что не только смещение, но и скорость, ускорение и сила представляют собой векторные величины, а законы движения должны описываться как соотношения между векторами.

Камень, вращающийся на веревке, удерживается на круговой орбите силой натяжения веревки. Точно, так же Луна удерживается на своей почти круговой орбите силой притяжения Земли, а планеты удерживаются на своих почти круговых орбитах силой притяжения Солнца. Каждая из этих сил действует в определенном направлении и имеет определенную величину. То же самое справедливо и в отношении других сил. В частности, сила реакции опоры, на которой покоится тело, направлена перпендикулярно поверхности опоры. Сказанное означает, что, подобно смещению, скорости и ускорению, сила – это направленная, т. е. векторная, величина.

При равномерном движении по окружности ускорение и сила, удерживающая частицу на круговой орбите, направлены к центру окружности. Это дает основание для следующего правила: ускорение частицы прямо пропорционально приложенной силе. Опыт показывает, что чем массивнее тело, тем меньшее ускорение сообщает ему данная приложенная сила, например сила со стороны пружины, сжатой до определенного размера.

spacemystery.ru

Скорость и ускорение. Среднее ускорение, мгновенное ускорение. Тангенциальное и нормальное ускорение. Полное ускорение.

⇐ ПредыдущаяСтр 2 из 5Следующая ⇒

Ускорение – это физическая величина, численно равная изменению скорости за единицу времени. Средним ускорением называется отношение изменения скорости к промежутку времени, за который это изменение произошло. Вычисляют среднее ускорение при помощи формулы: а_ср=∆V/∆t. Мгновенное ускорение тела в данный момент времени – это физическая величина, которая равна пределу, к которому стремится среднее ускорение при стремлении промежутка времени к 0. Другими словами – это ускорение, развиваемое телом за очень маленький отрезок времени: а

мг= lim_x-0(∆V/∆t) . Тангенциальным (касательным) ускорением называют ту составляющую вектора ускорения, которая направлена по касательной к траектории в данной точке траектории движения. Тангенциальное ускорение описывает степень изменения скорости по модулю при совершении криволинейного движения.

У вектора тангенциального ускорения вектор тангенциального ускорения направление такое же, как и у линейной скорости либо противоположно ему. Т.е. вектор тангенциального ускорения находится в одной оси с касательной окружности, являющейся траекторией движения тела.

Нормальным ускорением является та часть вектора ускорения, которая направлена по нормали к траектории движения в заданной точке на траектории движения тела. Т.е. вектор нормального ускорения расположен перпендикулярно к линейной скорости движения. Нормальное ускорение описывает степень изменения скорости по направлению и обозначается как вектор тангенциального ускорения. Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение при криволинейном движении составляется из тангенциального и нормального ускорений по правилу сложения векторов и вычисляется при помощи формулы: a²=a_t²+a_n² или а=корень(a_t²+a_n²). При помощи правила сложения векторов вычисляем и направление полного ускорения: a=a_t+a_n

4. Вращательное движение. Угловая скорость и угловое ускорение. Линейная скорость. Вращательным движением абсолютно твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела движутся в плоскостях, перпендикулярных к неподвижной прямой, называемой осью вращения, и описывают окружности, центры которых лежат на этой оси. Угловой скоростью

вращения называется вектор, численно равный первой производной угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта: Единица измерения угловой скорости радиан в секунду (рад/с).Таким образом, вектор ω определяет направление и быстроту вращения. Если ω=const, то вращение называется равномерным. Угловая скорость может быть связана с линейной скоростью υ произвольной точки А. Пусть за время Δt точка проходит по дуге окружности длину пути Δs. Тогда линейная скорость точки будет равна: При равномерном вращении его можно охарактеризовать периодом вращения Т – временем, за которое точка тела совершает один полный оборот, т.е. поворачивается на угол 2π: Число полных оборотов, совершаемых телом при равномерном движении по окружности, в единицу времени называется частотой вращения: откуда Для характеристики неравномерного вращения тела вводится понятие углового ускорения. Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

Линейной скоростью называется скорость, с которой точка движется по окружности. Точка, лежащая на окружности радиуса R, за один оборот пройдёт путь, равный длине окружности 2πR, за время, равное периоду Т. Взяв отношение пути 2πR ко времени T, мы получим скорость движения точки по окружности: v = 2πR/T Но 1/Т = n; следовательно, v = 2πRn

Отсюда легко установить связь между линейной и угловой скоростями. Мы уже знаем, что угловая скорость связана с числом оборотов формулой: ω = 2πn; поэтому на основании формулы скорости движения по окружности получим: v = ωR Известно, что вектор скорости точки, движущейся по окружности, направлен по касательной. Следовательно, линейная скорость направлена по касательной к окружности.

 

Рекомендуемые страницы:

lektsia.com

Ускорение – это… Что такое Ускорение?

Падающий мяч при отсутствии сопротивления воздуха ускоряется, то есть движется все быстрее и быстрее.

Ускоре́ние (обычно обозначается , в теоретической механике ) — производная скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости точки (тела) при её (его) движении за единицу времени (то есть ускорение учитывает не только изменение величины скорости, но и её направления).

Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².

Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду (m/s², м/с²), существует также внесистемная единица Гал (Gal), применяемая в гравиметрии и равная 1 см/с².

Производная ускорения по времени, то есть величина, характеризующая скорость изменения ускорения, называется рывок:

, где: — вектор рывка.

Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости материальной точки по времени:

.

Ускорение точки при прямолинейном движении

Если вектор не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:

.

Из вышеприведённых двух формул можно вывести ещё одну, связывающую скалярные величины:

Здесь — начальная скорость тела, — конечная скорость тела; — ускорение тела; — пройденный телом путь.

Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным.

Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное, вообще говоря, не верно).

Ускорение точки при движении по окружности

Вектор ускорения

при движении точки по окружности можно разложить на два слагаемых (компоненты):

Тангенциальное ускорение — направлено по касательной к траектории (обозначается иногда и т. д., в зависимости от того, какой буквой в данной книге принято обозначать ускорение). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.

Центростремительное или Нормальное ускорение  — возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) (также обозначается иногда и т. д.). Является составляющей вектора ускорения a, перпендикулярной вектору мгновенной скорости. Характеризует изменение скорости по направлению. Вектор нормального ускорения всегда направлен к центру окружности, а модуль равен:

Угловое ускорение — показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:

Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растёт, и наоборот.

Ускорение точки при движении по кривой

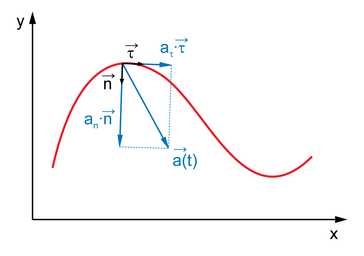
Вектор ускорения можно разложить по сопутствующему базису :

,

где

, называемое бинормальным ускорением, всегда равно нулю. Это можно считать прямым следствием определения векторов : можно сказать, что они выбираются именно так, чтобы первый всегда совпадал с нормальным ускорением, второй же ортогонально первому.

Векторы и называются касательным (тангенциальным) и нормальным ускорениями соответственно.

Итак, учитывая сказанное выше, вектор ускорения всегда можно записать как:

,

Ускорения в твёрдом теле

Связь ускорений двух точек можно получить, продифференцировав формулу Эйлера для скоростей по времени:

,

где  — вектор угловой скорости тела, а  — вектор углового ускорения тела.

Второе слагаемое называется осестремительным ускорением.

Ускорение при сложном движении

Говорят, что материальная точка (тело) совершает сложное движение, если она движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. Тогда абсолютное ускорение тела равно сумме относительного, переносного и кориолисова:

.

Первый закон Ньютона постулирует существование инерциальных систем отсчёта. В этих системах отсчёта равномерное прямолинейное движение имеет место в том случае, когда тело (материальная точка) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом, постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчёта всегда является некоторое внешнее силовое воздействие.

Второй закон Ньютона утверждает, что ускорение материальной точки всегда пропорционально приложенной к ней и порождающей ускорение силе, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется массой материальной точки):

Единицы измерения ускорения

• метр на секунду в квадрате (метр в секунду за секунду), м/с², производная единица системы СИ
• сантиметр на секунду в квадрате (сантиметр в секунду за секунду), см/с², производная единица системы СГС

Преобразования между различными единицами ускорения

	м/с2	фут/с2	g0	см/с2
1 м/с2 =	1	3.28084	0.101972	100
1 фут/с2 =	0.304800	1	0.0310810	30.4800
1 g0 =	9.80665	32.1740	1	980.665
1 см/с2 =	0.01	0.0328084	0.00101972	1

Измерение ускорения

Приборы для измерения ускорения называются акселерометрами. Они не измеряют ускорение непосредственно, а измеряют силу реакции (укр.)русск. опоры, которая возникает при ускоренном движении. Поскольку аналогичные силы сопротивления возникают также и в поле тяготения, то с помощью акселерометров можно измерять также и гравитацию.

Акселерографы — приборы, измеряющие и автоматически записывающие (в виде графиков) значения ускорения поступательного и вращательного движения.

Примеры ускорений

Значения ускорений различных движений:^[1]

Примечание: g ≈ 9,81 м/с².

См. также

Примечания

1. ↑ Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике. — 10-е, испр. и доп.. — М.: Наука, 1988. — С. 61. — 256 с. — ISBN 5-02-013833-9

Ссылки

• Ландау, Л. Д., Лифшиц, Е. М. Механика. — Издание 5-е, стереотипное. — М.: Физматлит, 2004. — 224 с. — («Теоретическая физика», том I). — ISBN 5-9221-0055-6

dis.academic.ru

Скорость и ускорение точки

Одной из основных характеристик движения точки является ее скорость относительно выбранной системы отсчета, которая изображена в виде декартовой прямоугольной системы координат (рис. 21).

Положение движущейся точки относительно рассматриваемой системы отсчета определяется в момент времени радиусом-вектором , который соединяет неподвижную точку с этой точкой. В другой момент времени движущаяся точка займет положение и ее радиусом-вектором будет . За время радиус-вектор движущейся точки изменится на .

Средней скоростью точки за время называют отношение , т.е.:

.

Средняя скорость параллельна вектору . В общем случае она зависит от времени осреднения . У нее нет конкретной точки приложения на траектории.

Введем скорость точки в момент , которая определяется как предел средней скорости, если промежуток времени, за который определяется средняя скорость, стремится к нулю, т. е.

.

Скорость точки направлена в сторону ее движения по предельному направлению вектора при , стремящемся к нулю, т.е. по предельному направлению секущей , которая совпадает с касательной к траектории в точке . Таким образом, скорость точки равна первой производной по времени от ее радиуса-вектора. Она направлена по касательной к траектории в сторону движения точки.

Начало радиуса-вектора движущейся точки можно выбрать в любой неподвижной точке. На рис. 21 представлен случай, в котором радиусом-вектором является также с началом в точке . Радиусы-векторы имеют одинаковые изменения и за время и поэтому

. (44)

Пусть движущаяся точка в момент времени имеет скорость . В момент времени эта точка занимает положение , имея скорость (рис. 22). Чтобы изобразить приращение скорости за время , перенесем вектор скорости параллельно самому себе в точку .

Средним ускорением точки за время называют отношение , т.е. . Среднее ускорение точки параллельно приращению скорости . Как и средняя скорость, среднее ускорение не имеет на траектории конкретной течки приложения и изображено в точке условно. В общем случае среднее ускорение зависит от времени .

Ускорением точки в момент времени называют предел, к которому стремится среднее ускорение при , стремящемся к нулю, т. е.

. (45)

Таким образом, ускорение точки равно первой производной по времени от скорости точки.

Приращение скорости и, следовательно, среднее ускорение направлены внутрь вогнутости траектории. Так же направлены и их предельные значения при , стремящемся к нулю. Поэтому ускорение точки направлено тоже внутрь вогнутости траектории.

Ускорение точки можно представить в виде (рис. 23):

. (46)

Часть ускорения, равная

,

называется касательной составляющей ускорения. Она направлена по касательной к траектории. Другая часть ускорения

называется нормальной составляющей ускорения ( – радиус кривизны траектории). Она направлена внутрь вогнутости траектории, перпендикулярно .

2.1.2. Векторный способ задания движения точки

Движение точки относительно рассматриваемой системы отсчета при векторном способе изучения движения задается радиусом-вектором этой точки (рис. 24). Движение точки считается заданным, если известен радиус-вектор движущейся точки как функция времени, т. е.

. (47)

Задание векторного уравнения движения (47) полностью определяет движение точки.

Скорость точки направлена по касательной к траектории и вычисляется, согласно ее определению, по формуле:

. (48)

Для ускорения точки соответственно имеем

. (49)

Определение скорости и ускорения точки сводится к чисто математической задаче вычисления первой и второй производных по времени от радиуса-вектора этой точки.

Похожие статьи:

poznayka.org

Вопрос 1.2. Скорость и ускорение.

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Линия, которую очерчивает материальная точка в пространстве при своем движение называется траекторией движения. Пусть М₀ – начальное положение точки, а М- текущее положение. Направленный отрезок, соединяющий начальное и текущее положение точки называется перемещением – . Перемещение является приращением радиуса-вектора материальной точки: .

Пусть ∆S – длина траектории между двумя положениями точки в пространстве.

Средняя скорость по пути – это отношение пути к промежутку времени за которое этот путь пройден: -средняя скорость по пути (скалярная величина).

Средняя скорость по перемещению: – средняя скорость по перемещению – это отношение перемещения к промежутку времени, за которое это перемещение произошло. Это вектор направленный вдоль перемещения. – мгновенная скорость по пути – это предел средней скорости по пути при стремлении промежутка времени к нулю или это первая производная от пути по времени. – вектор скорости – это предел средней скорости по перемещению при стремлении промежутка времени к нулю, по другому – это первая производная от радиус вектора по времени.

При уменьшении промежутка времени текущее положении точки приближается к начальному положению, при этом уменьшается разность между значениями пути и перемещения.

Направленное перемещение приближается к направлению касательной к траектории движения проведенной через точку М₀. Поэтому вектор скорости совпадает с направлением касательной к траектории движения.

Пусть – единичный вектор направленный по касательной к траектории движения, тогда можно написать. Т.к. , то скорость

где – составляющие ск-и по осям координат.

 

 

Ускорение.

Характеристика изменения скорости определяется ускорением.

Средние ускорение: . Вектор направленный по направлению приращения скорости. Ускорение равняется отношению приращения скорости к промежутку времени. За которое это приращение произошло. – приращение скорости.

Т.к. ; Обозначим первое слагаемое через

-касательная или тангенсальная составляющая ускорения показывает

скорость изменения величины скорости. – нормальное или центростремительная составляющая ускорения.

Здесь: – нормаль к траектории – единичный вектор, направленный перпендикулярно к траектории в сторону вогнут. Таким образом . Здесь ρ-радиус кривизны траектории. Таким образом нормальное составляющее a_n направлено в направлении центра кривизны траектории и показывает скорость изменения направления движения. В итоге вектор ускорения можно представить как векторная сумма двух взаимно-перпендикулярных составляющих . Ускорение – вектор, направленный под углом к траектории движения и равняется первой производной от вектора скорости по времени и показывает изменение скорости за единицу времени. Т.к. ;

Здесь: составляющая ускорения по координатным осям.

;

Вопрос 1.3. Простейшие виды движения материальной точки.

1) -равномерное движение по прямой. ;

2) ; a_n=const равномерное вращение по окружности ;

3) ; a_n=0. равномерное движение.

a>0 – равноускоренное движение. a<0 равнозамедленное движение.

;

4) -равнопеременное вращение по окружности

;

Вопрос 1.4. Угловая скорость и угловое ускорение.

При движение по окружности используется понятие угла поворота. -это отношение дуги окружности между двумя положениями радиус вектора к радиусу окружности. (единица измерения угла безразмерн. в-на.)

Средняя угловая скорость: ; 1/с=(Гц) – это отношение угла поворота к промежутку времени.

Угловая скорость:

Угловая скорость считается векторной величиной направленной по оси вращения так, что если посмотреть с конца вектора вращения видно против часовой стрелки.

Т.к. ; ;

Среднее угловое ускорение , (1/с²).

Угловое ускорение:

Здесь: -приращение угловой скорости.

Если угловая скорость с течением времени увеличивается, то направление ω и β совпадают. Если угловая скорость уменьшается, то их направления противоположны. Т.к. , то ; ;

Вопрос 1.5. Законы Ньютона.

I закон Ньютона: Если ни тело не действует, другие тела или действие этих тел скомпенсировано, то тело находится в состоянии покоя или равномерного прямолинейного движения. Если , то . Системы отсчета, где выполняется первый закон Ньютона, называются инерциальными. В противном случае системы называются неинерциальными. Никакими механическими опытами проводимыми внутри инерциальной системы отсчета нельзя установить движется эта система или нет по другому законы механики выполняются одинаково во всех инерциальных системах отсчета. Разные инерциальные системы могут двигаться относительно друг друга равномерно и прямолинейно. В этом заключается механический принцип относительности.

II закон Ньютона: . Ускорение с которым движется тело прямо пропорциональна равнодействующей всех сил действующих на тело и обратно пропорциональна массе тела.

Здесь: -результирующая сила или равнодействующая всех сил. Сила – это физическая величина, показывающая взаимодействие двух тел, в результате этого взаимодействия изменяется или состояние движения тел или тела деформируется. Масса- это физическая величина, определяющая кол-во в данном теле и меру его инертности. Инертность – это способность тела сохранять состояние движения. , m₀ – масса покоя; – скорость света. Из II закона:

III закон Ньютона: Два тела взаимодействуют между собой с силами равными по величине и противоположно направлены.

 

Рекомендуемые страницы:

lektsia.com

---