Ускорение векторное – Вектор – среднее ускорение – Большая Энциклопедия Нефти и Газа, статья, страница 1
- Комментариев к записи Ускорение векторное – Вектор – среднее ускорение – Большая Энциклопедия Нефти и Газа, статья, страница 1 нет
- Советы абитуриенту
Положение, смещение, скорость и ускорение как векторы
Физика > Положение, смещение, скорость и ускорение как векторы
Положение, смещение, скорость и ускорение могут отображаться в качестве векторов, потому что определяются в терминах величины направления.
Задача обучения
- Изучить использование векторов при анализе физических величин.
Основные пункты
- Векторы – стрелки, вмещающие величину и направление. Их применяют в физике для отображения физических величин.
- Смещение – дистанция от объекта к контрольной точке. Оно располагает протяжностью к точке отсчета и направлением, поэтому прекрасно изображается вектором.
- Векторная скорость – скорость изменения положения со временем. Чтобы вычислить ее, нужно понять, как быстро меняется смещение и в каком направлении.
- Ускорение – изменение векторной скорости, требующее величины и направления.
- При изображении векторов может не хватить места, чтобы привлечь их к реальному масштабу, поэтому важно не забывать, какой именно масштаб вы выбрали.
Термины
- Смещение – длина и направление прямой линии между двумя объектами.
- Ускорение – темп изменения скорости со временем.
Пример
На рисунке продемонстрирован пример использования вектора для визуального отображения объекта в физике.
Использование векторов
Векторы используют для отображения физических величин. Чаще всего ими изображают смещение, скорость и ускорение. Комбинация величины и направления выливается в виде стрелки. Длина отмечает величину, а направление показывается кончиком стрелы.
Применения
В физике векторы приносят много пользы, потому что визуально демонстрируют положение, скорость, смещение и ускорение. Если вы рисуете векторы, то можете столкнуться с нехваткой места, чтобы отобразить в полноценном масштабе. Но все можно исправить, если помнить о масштабе. Например, величину 100 можно отобразить длиной в 5 единиц при масштабе 120. Когда инверсия масштаба умножается на отображенную величину, она должна приравниваться к фактической величине.
Положение и смещение
Смещение – дистанция в любом направлении от объекта. Вектор здесь применяется в качестве визуализации перемещения. Вектор позиции отображает позицию объекта вначале координат. Вектор положения отображает позицию относительно контрольной точки, вторичного объекта или изначального положения. Вектор положение – прямая линия, проведенная от любого начала к объекту.
Скорость
Определяется величиной и направлением. Чтобы указать, что объект набирает скорость или тормозит, нужно знать направление. Например, самолет со скоростью 200 км/ч, отправляющийся на северо-восток, отображается вектором в том же направлении и скорости. Величина важна только в качестве сравнения векторов с другим объектом.
Ускорение
Это характеристика изменения скорости, представленная величиной и направлением. Эти значения очень важны. Например, в диаграмме свободного тела полезно использовать вектор ускорения возле объекта, чтобы отметить ускорение в направлении поверхности. Если гравитация выступает единственной влияющей силой, то вектор укажет вниз с величиной 9.81 м/с
Мы видим человека, взбирающегося на холм. Направление движения определяется углом тета относительно вертикальной оси и длины стрелки, поднимающейся вверх. Также он ускоряется вниз из-за влияния силы тяжести
v-kosmose.com
§3. Вектор скорости.
Для характеристики быстроты движения вводится понятие скорости.
Определение: Средней
скоростью движения точки за интервал
времени от 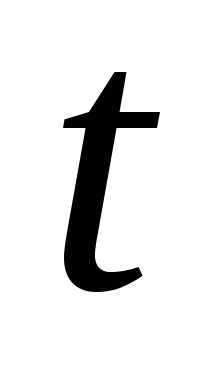 до
до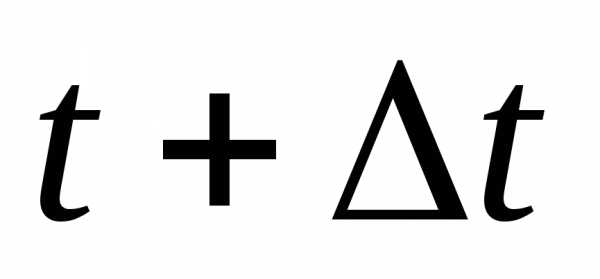 называется
векторная величина равная отношению
приращения радиус-вектора точки за этот
промежуток времени к его продолжительности
называется
векторная величина равная отношению
приращения радиус-вектора точки за этот
промежуток времени к его продолжительности .
.
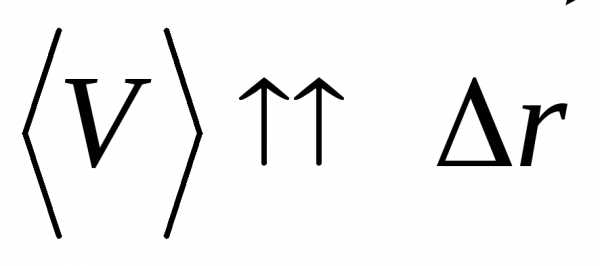
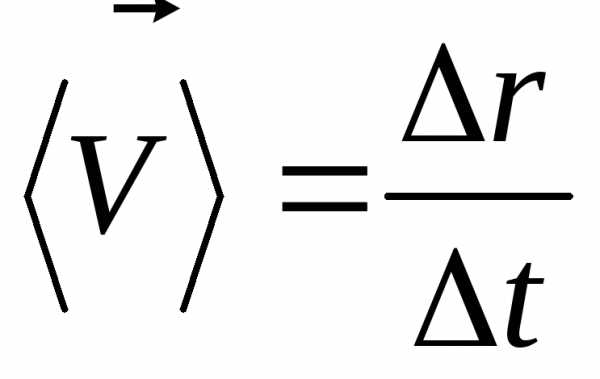 – средняя скорость.
– средняя скорость.
Определение: Скорость (или мгновенная скорость) точки называется векторная величина, равная первой производной по времени от радиус-вектора.
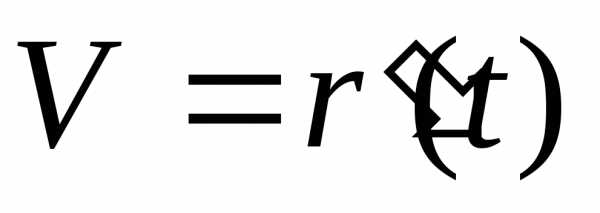
Вектор скорости характеризует движение, как по величине, так и по направлению. Вектор скорости всегда направлен по касательной к траектории в сторону движения.
Определение: Модуль скорости равен первой производной по времени от пройденного пути.
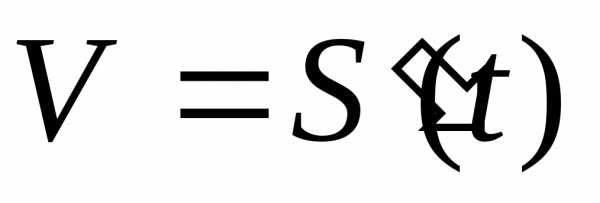
Разложим вектор скорости по базису прямоугольной декартовой системы координат:
, гдеVx, Vy, Vz проекции вектора скорости на соответствующую ось, которые соответственно равны:
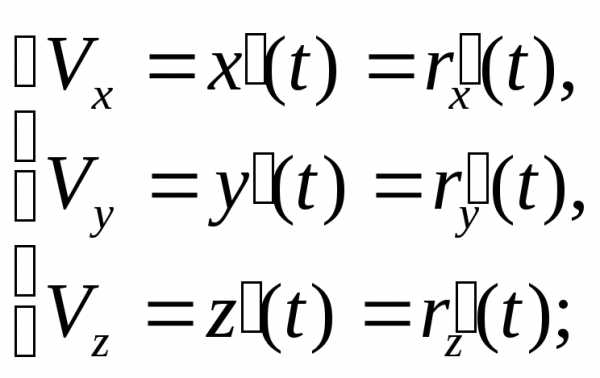
где – это иксовая проекция радиус-вектора материальной точки.
 В координатном
представлении вектор скорости имеет
вид:
В координатном
представлении вектор скорости имеет
вид:
Модуль вектора скорости в координатном представлении:
Обратное соотношение.
Представим радиус вектор скорости посредством определенного и неопределенного интеграла:
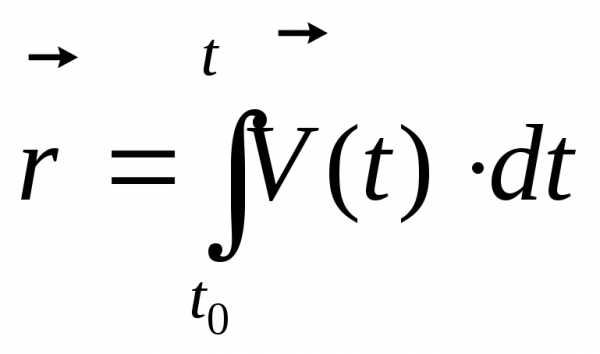
где t, t0 – начальный и конечный момент времени.
Представление пройденного пути через модуль скорости посредством определенного и неопределенного интеграла.
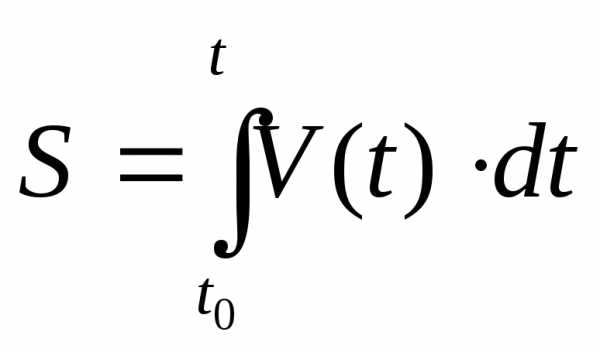
§4. Вектор ускорения.
Для характеристики быстроты изменения вектора скорости точки в механике вводится понятие ускорения.
Определение: Среднее
ускорение за интервал времени от 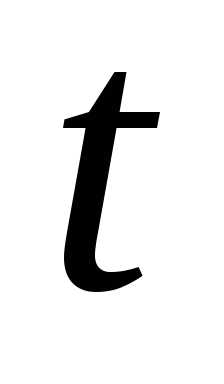 до
до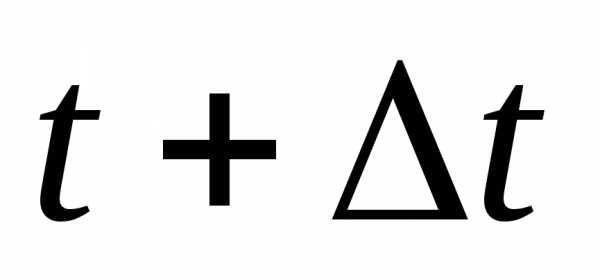 называется векторная величина равная
отношению приращения вектора скорости
точки за данный интервал времени к его
величине.
называется векторная величина равная
отношению приращения вектора скорости
точки за данный интервал времени к его
величине.
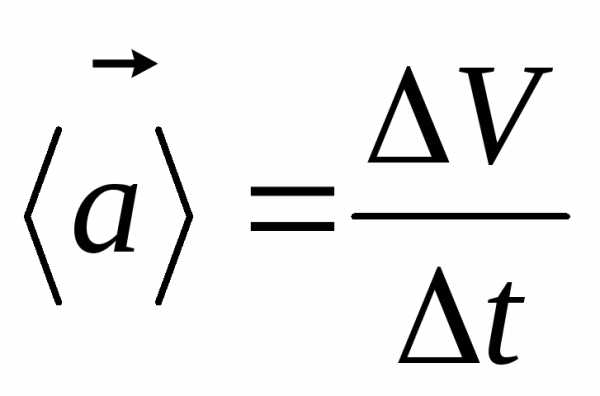
Определение: Ускорение (или мгновенное ускорение) точки называется векторная величина, численно равная первой производной по времени от скорости рассматриваемой точки или, что то же самое, вторая производная по времени от радиус-вектора этой точки:
Ускорение можно ввести через предел от среднего ускорения:
Две введенные записи ускорения являются эквивалентными.
Разложим вектор ускорения по базису прямоугольной декартовой системы координат:
где ax, ay, az – проекции вектора ускорения на ось.
Координатное представление модуля вектора ускорения:
Обратные соотношения: ; 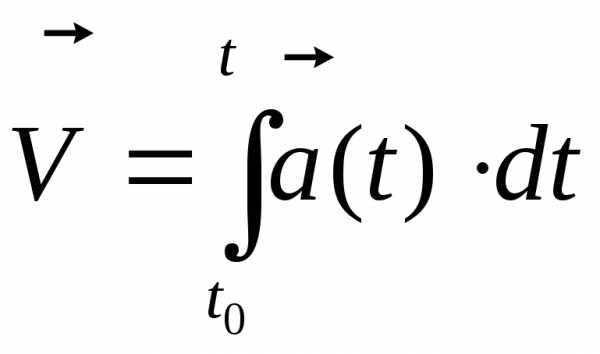
Рассмотрим движение
материальной точки вдоль плоской кривой.
Ускорение всегда направлено внутрь
вогнутости кривой или траектории. Введем
два единичных вектора:  ,
который направлен по касательной к
траектории и
,
который направлен по касательной к
траектории и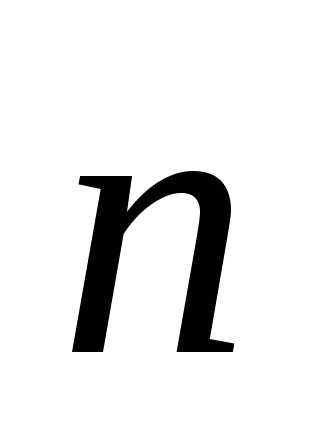 – направлен перпендикулярно траектории
в центр кривой.
– направлен перпендикулярно траектории
в центр кривой.
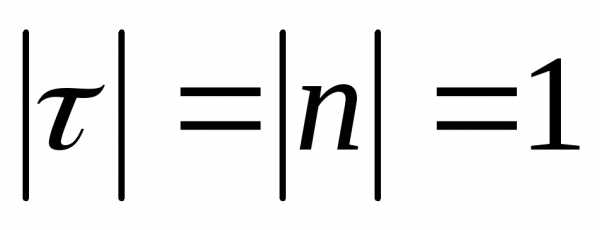 ;
;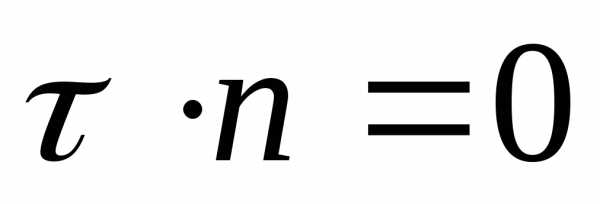
Разложим вектор ускорения по заданным направлениям.
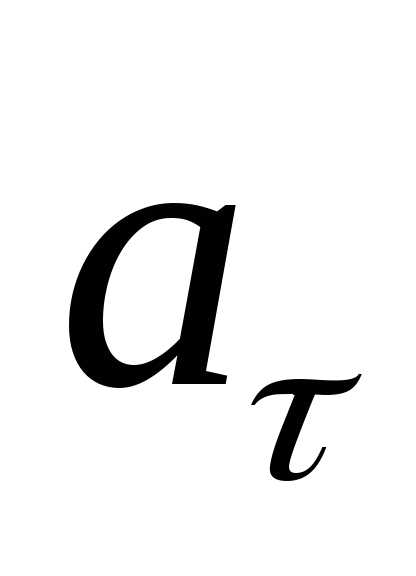 – касательное
ускорение.
– касательное
ускорение.
Определение: Касательное ускорение – векторная величина, характеризующая быстроту изменения вектора скорости по модулю.
– векторное представление.
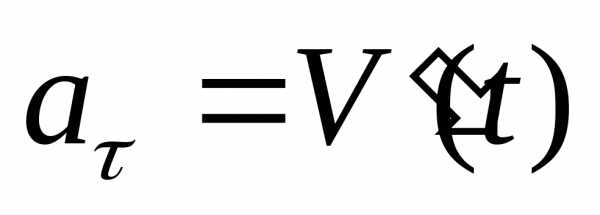 – скалярное
представление.
– скалярное
представление.
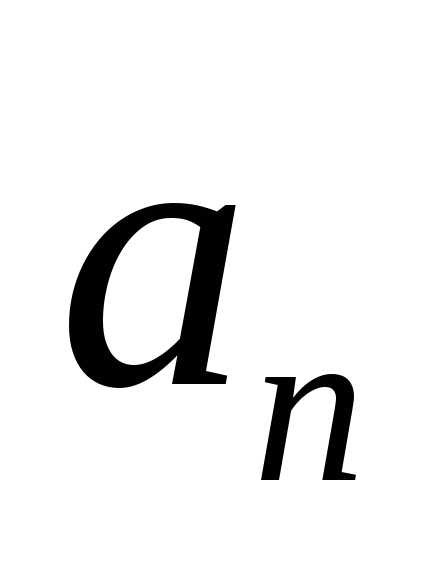 – нормальное
ускорение.
– нормальное
ускорение.
Определение: Нормальное ускорение характеризует быстроту изменения вектора скорости по направлению и вычисляется по формуле:
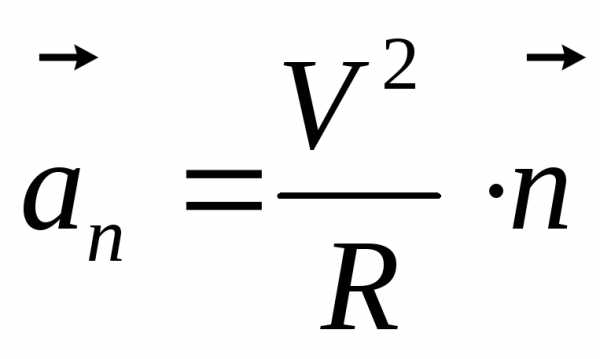 -где R- радиус
кривизны траектории в точке М
-где R- радиус
кривизны траектории в точке М
Если траектория – окружность, то R – радиус окружности.
В скалярном представлении:
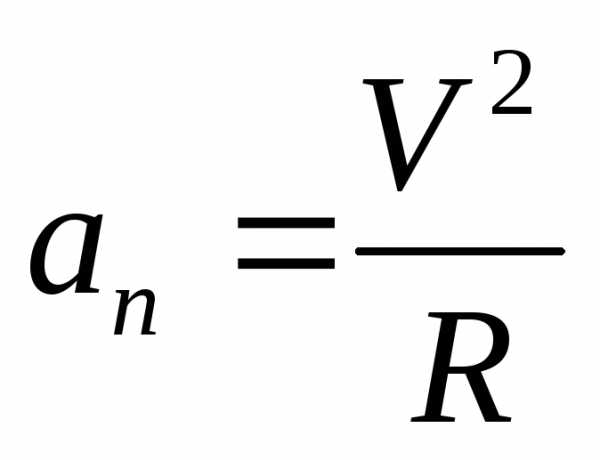
Из свойств составляющих полное ускорение следует, что полное ускорение направленно в сторону вогнутости траектории.
Модуль полного ускорения равен:
Аналогично для вектора полного ускорения:
studfiles.net
Векторные формулы для скоростей и ускорений точек тела
В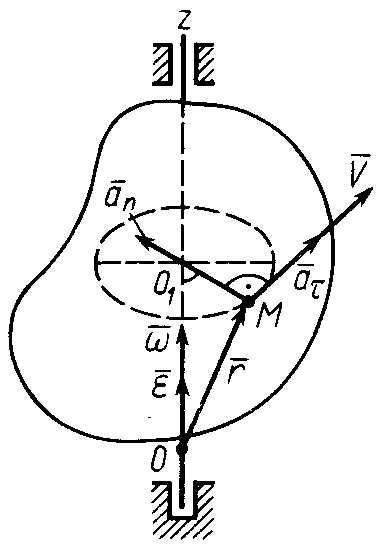 ыразим
скорость, касательное, нормальное и
полное ускорения точки тела в векторной
форме (рис. 32). Скорость точки по модулю
и направлению можно представить векторным
произведением
ыразим
скорость, касательное, нормальное и
полное ускорения точки тела в векторной
форме (рис. 32). Скорость точки по модулю
и направлению можно представить векторным
произведением
, (75)
г
Рис. 32
де – радиус-вектор точки
– радиус-вектор точки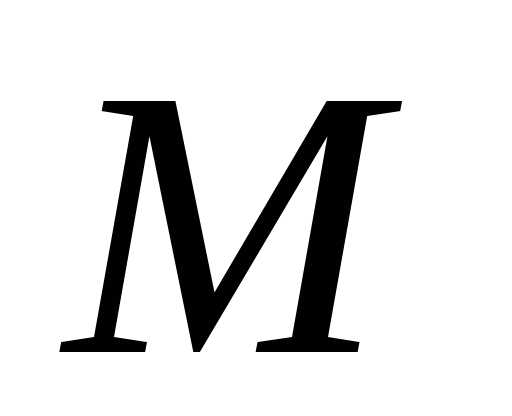 ,
проведенный из произвольной точки оси
вращения
,
проведенный из произвольной точки оси
вращения ,
например точки
,
например точки
Из определения ускорения и векторной формулы Эйлера имеем:
. (76)
Первое слагаемое в (76) является касательным ускорением, а второе – нормальным, т. е.
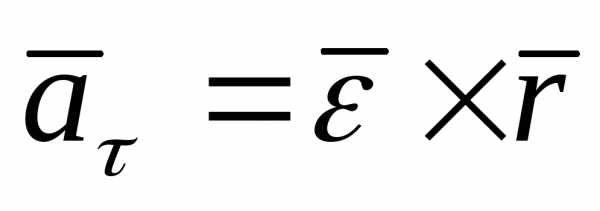 ,
. (77)
,
. (77)
2.3. Сложное движение точки
Для изучения некоторых, более сложных видов движений твердого тела целесообразно рассмотреть простейшее сложное движение точки. Во многих задачах движение точки приходится рассматривать относительно двух (и более) систем отсчета, движущихся друг относительно друга. Так, движение космического корабля, движущегося к Луне, требуется рассматривать одновременно и относительно Земли и относительно Луны, которая движется относительно Земли. Любое движение точки можно считать сложным, состоящим из нескольких движений.
В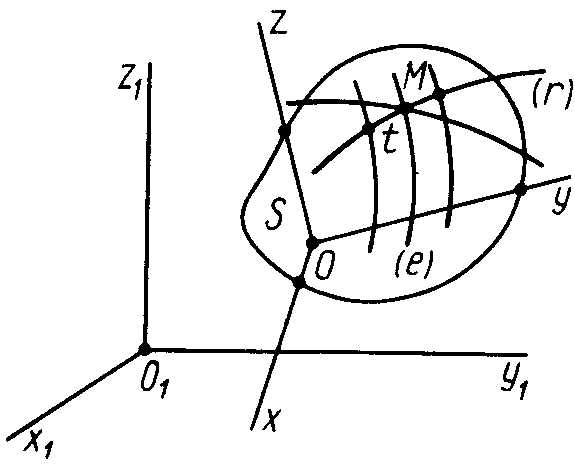
Рис. 33
простейшем случае сложное движение точки состоит из относительного и переносного движений. Определим эти движения. Пусть имеем две системы отсчета, движущиеся друг относительно друга. Если одну из этих систем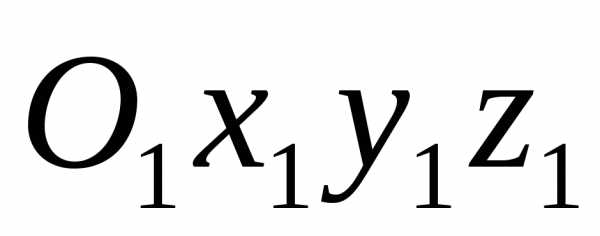 (рис. 33) принять за основную или неподвижную
(ее движение относительно других систем
отсчета не рассматривается), то вторая
система отсчета
(рис. 33) принять за основную или неподвижную
(ее движение относительно других систем
отсчета не рассматривается), то вторая
система отсчета будет двигаться относительно первой.
Движение точки относительноподвижной системы отсчета
будет двигаться относительно первой.
Движение точки относительноподвижной системы отсчета  называется относительным. Характеристики
этого движения, такие, как траектория,
скорость и ускорение, называютсяотносительными.
Их обозначают индексом
называется относительным. Характеристики
этого движения, такие, как траектория,
скорость и ускорение, называютсяотносительными.
Их обозначают индексом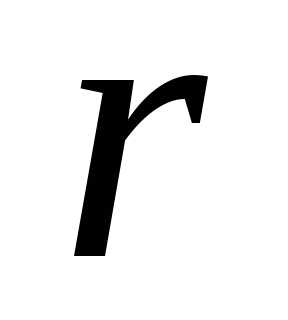 ;
для скорости и ускорения
;
для скорости и ускорения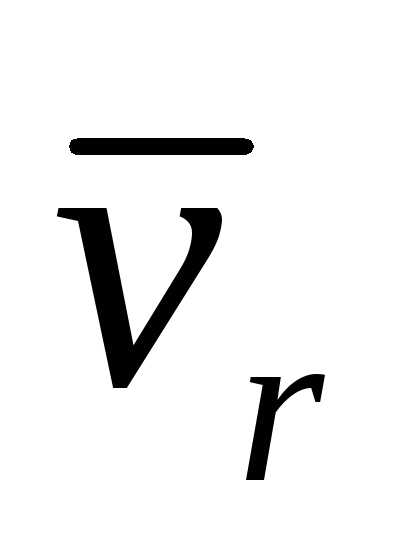 и
и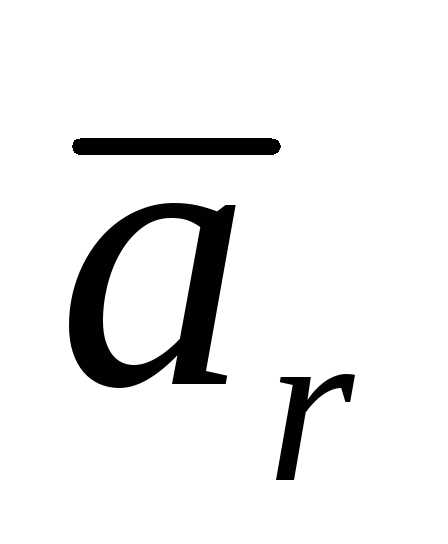 .
Движение точки относительноосновной,
или неподвижной,
системы отсчета
.
Движение точки относительноосновной,
или неподвижной,
системы отсчета 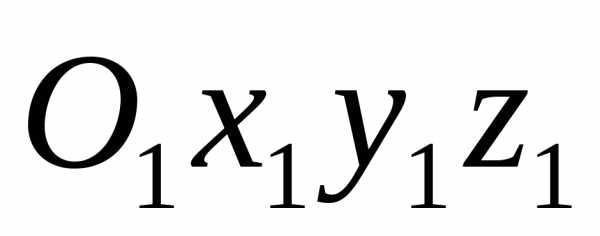 называетсяабсолютным (или сложным).
Его также иногда называют составным движением. Траектория, скорость и
ускорение этого движения называются
абсолютными. Скорость и ускорение
абсолютного движения обозначают буквами
называетсяабсолютным (или сложным).
Его также иногда называют составным движением. Траектория, скорость и
ускорение этого движения называются
абсолютными. Скорость и ускорение
абсолютного движения обозначают буквами  и
и без индексов.Переносным движением называют движение подвижной
системы отсчета по отношению к неподвижной.
Вследствие относительного движения
движущаяся точка в различные моменты
времени совпадает с различными точками
тела
без индексов.Переносным движением называют движение подвижной
системы отсчета по отношению к неподвижной.
Вследствие относительного движения
движущаяся точка в различные моменты
времени совпадает с различными точками
тела  ,
с которым скреплена подвижная система
отсчета. Переносной скоростью и переносным
ускорением являются скорость и ускорение
той точки тела
,
с которым скреплена подвижная система
отсчета. Переносной скоростью и переносным
ускорением являются скорость и ускорение
той точки тела ,
с которой в данный момент совпадает
движущаяся точка. Переносные скорость
и ускорение обозначают
,
с которой в данный момент совпадает
движущаяся точка. Переносные скорость
и ускорение обозначают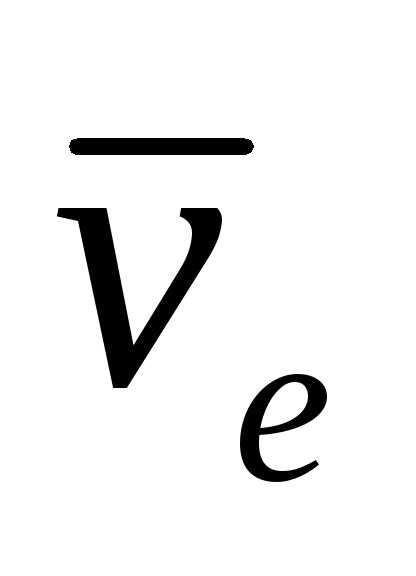 и
и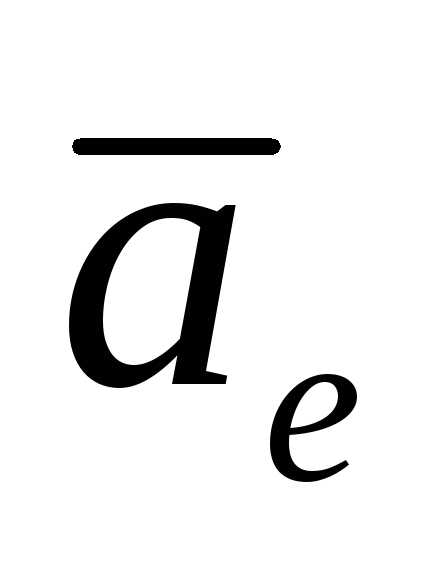 .
.Теорема сложения скоростей: скорость абсолютного движения точки равна векторной сумме скоростей переносного и относительного движений этой точки
. (78)
Так как в общем случае скорости переносного и относительного движений не перпендикулярны, то
.
Абсолютную скорость можно представить в виде:
. (79)
Скорость
является
скоростью точки свободного твердого
тела, скрепленного с подвижной системой
координат, с которой в данный момент
совпадает точка 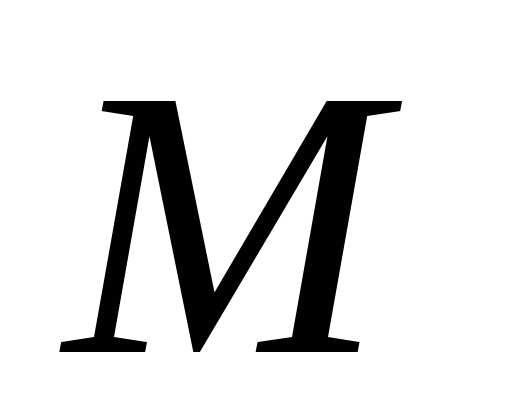 в движении тела относительно неподвижной
системы осей координат. Это есть
переносная скорость точки
в движении тела относительно неподвижной
системы осей координат. Это есть
переносная скорость точки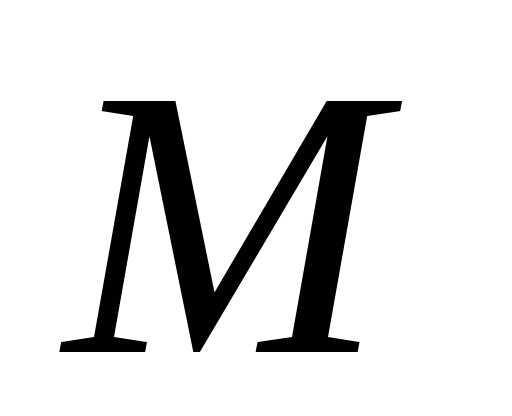 .
.
Теорема сложения ускорений точки (кинематическая теорема Кориолиса): абсолютное ускорение точки является векторной суммой трех ускорений – переносного, относительного и Кориолиса
, (80)
где
. (81)
Ускорение 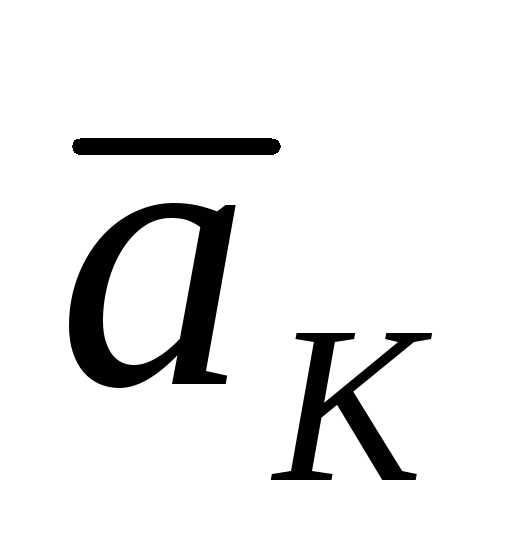 называетсяускорением
Кориолиса.
Иногда его также называют добавочным (или поворотным)
ускорением.
называетсяускорением
Кориолиса.
Иногда его также называют добавочным (или поворотным)
ускорением.
Абсолютное ускорение можно также представить в виде:
. (82)
В
этой формуле первые три слагаемых
составляют ускорение точки свободного
твердого тела в общем случае его движения
вместе с подвижной системой осей
координат относительно неподвижной.
Первое слагаемое 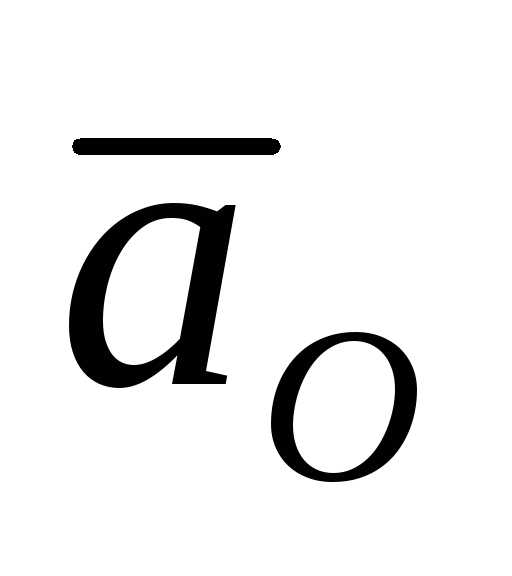 – ускорение точки
– ускорение точки ,
,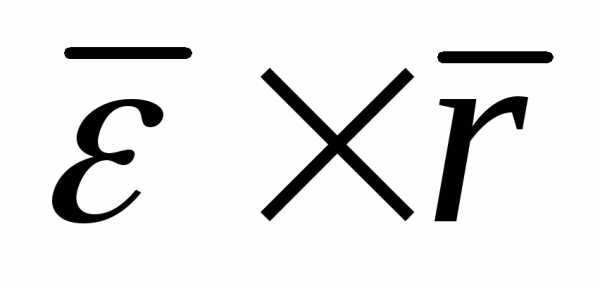 и– соответственно вращательное и
нормальное ускорения точки
и– соответственно вращательное и
нормальное ускорения точки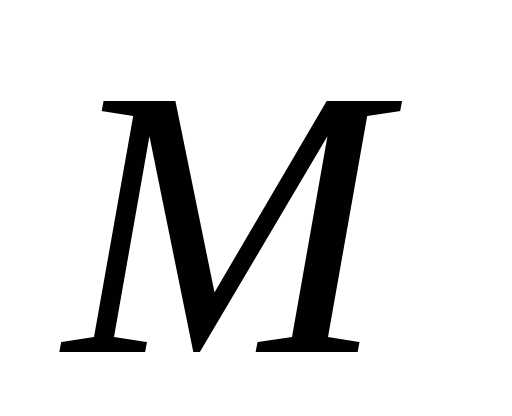 ,
если бы она двигалась только вместе с
подвижной системой осей координат, не
имея в рассматриваемый момент времени
относительного движения.
,
если бы она двигалась только вместе с
подвижной системой осей координат, не
имея в рассматриваемый момент времени
относительного движения.
При координатном способе задания в декартовых координатах
,
где 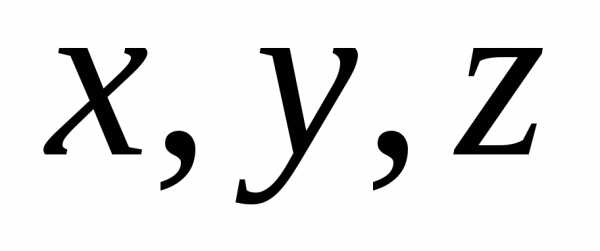 – координаты движущейся точки относительно
подвижной системы осей координат;
– координаты движущейся точки относительно
подвижной системы осей координат;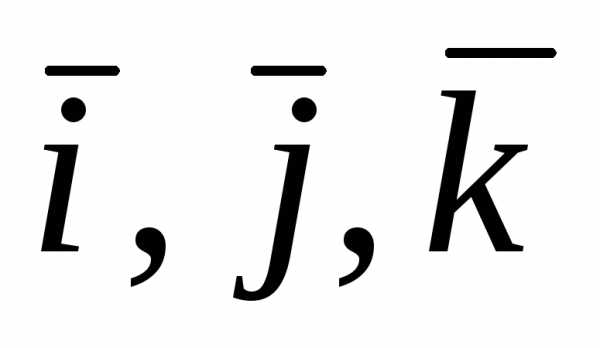 – единичные векторы этих осей. При
естественном способе задания движения
– единичные векторы этих осей. При
естественном способе задания движения
, 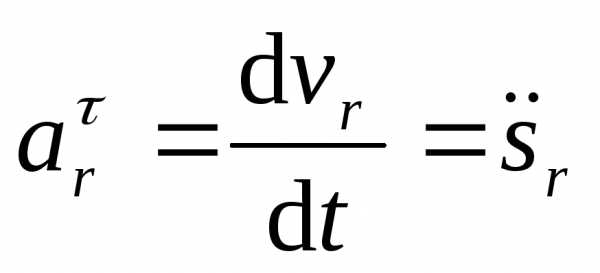 ,
,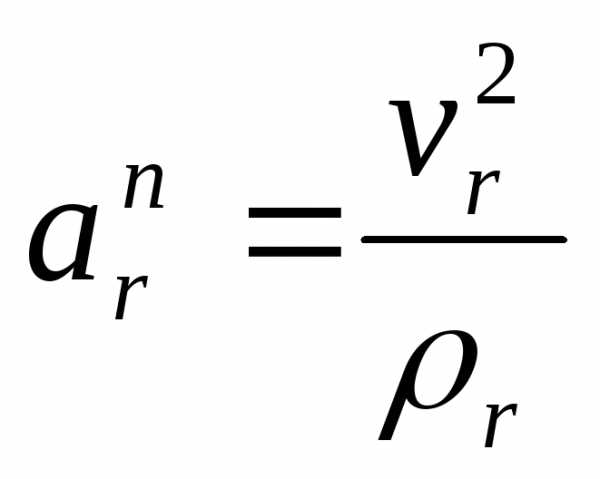 ,
,
где 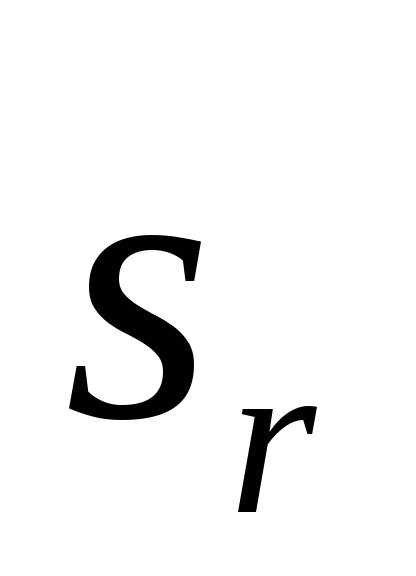 – расстояние от начала отсчета до точки
по траектории относительного движения;
– расстояние от начала отсчета до точки
по траектории относительного движения;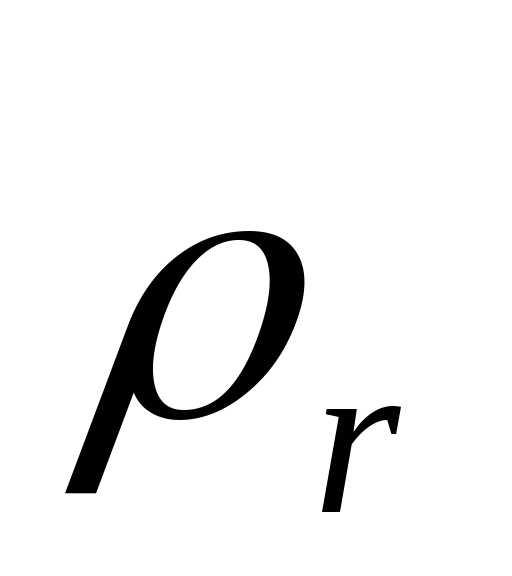 – радиус кривизны этой траектории. В
частном случае, когда переносное движение
есть вращение вокруг неподвижной оси,
переносное ускорение
– радиус кривизны этой траектории. В
частном случае, когда переносное движение
есть вращение вокруг неподвижной оси,
переносное ускорение
,
где касательное переносное ускорение
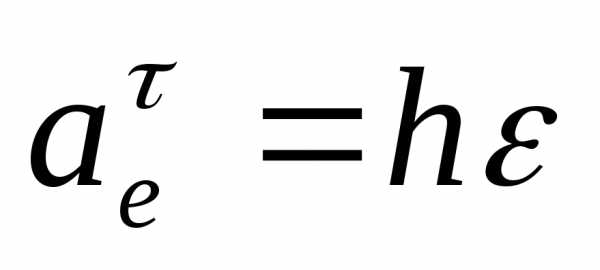 ,
,
причем 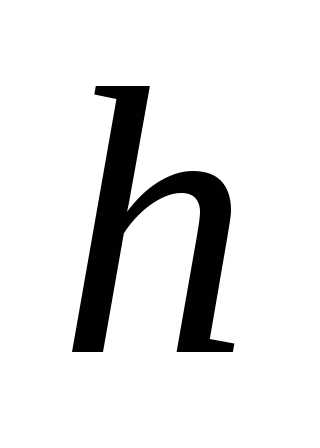 – кратчайшее расстояние от движущейся
точки до оси вращения. Нормальное
переносное ускорение
– кратчайшее расстояние от движущейся
точки до оси вращения. Нормальное
переносное ускорение
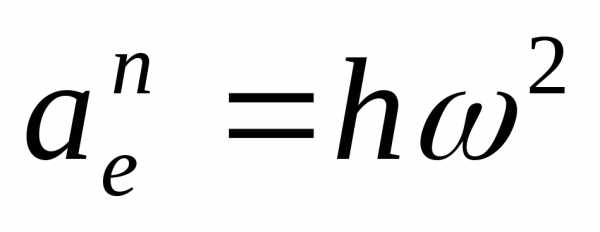 .
.
Абсолютное ускорение в этом случае
. (83)
studfiles.net
Найти вектор скорости и ускорения точки, примеры решений
В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора — вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами — единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? «Наверное какой-то жуткий», подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Вектор скорости материальной точки
Всем известно, что скорость материальной точки — это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Как найти вектор ускорения материальной точки
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора — это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему «механика твердых тел». А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
artsybashev.ru
Вектор ускорения
Энергетика Вектор ускоренияпросмотров – 153
Вектор скорости
В общем случае движения тела неравномерно. Скорость точки меняется. По этой причине вводят понятие средней скорости как величины равной длине пути, пройденной телом за некоторый промежуток времени . Различия в скоростях в моменты времени и будут тем меньше, чем ближе эти моменты времени. Величина
принято называть мгновенной скоростью.
Вспомним, что , в связи с этим можем записать:
.
Вектор мгновенной скорости при криволинейном движении, как и элементарное перемещение, направлен по касательной к траектории.
Проекции вектора скорости на оси координат определяют скорости по трем направлениям движения. Ясно, что
.
Размерность скорости .
Ускорение характеризует темп изменения скорости. Как и ранее, вводится понятие среднего ускорения и в случае имеем величину, характеризующую мгновенное ускорение:
.
Размерность ускорения .
Соответствующие компоненты ускорения в Декартовой системе координат бывают представлены в виде:
, , .
В случае прямолинейного движения вектор ускорения направлен параллельно вектору скорости. Движение может быть ускоренным или замедленным. Ускорение может быть постоянной величиной (равноускоренное или равнозамедленное движение) или переменной.
В случае криволинейного движения всегда существует ускорение, определяющее изменение скорости как векторной величины, нормальное ускорение ( ). В случае если движение вдоль траектории неравномерно, то есть и тангенциальное ускорения ( ). Нормальное ускорение всегда направлено вдоль радиуса кривизны траектории движения тела, в направлении изменения скорости как векторной величины, и принято называть центростремительным ускорением.
, ,
где – тангенциальная скорость движения тела (скорость вдоль траектории движения), – радиус кривизны траектории.
В случае равномерного движения тела (материальной точки) по окружности, .
Размерность ускорения:
Ниже представлена таблица первых производных и неопределенных интегралов от некоторых элементарных функций, знание которых крайне важно для понимания излагаемого далее материала.
где С = const и принято называть константой интегрирования. При решении задач она определяется какими-либо граничными условиям.
Производная по от произведения двух функций
Производная по от отношения двух функций
Пример: определение зависимостей скорости прямолинейного движения и пройденного материальной точкой пути от времени при равноускоренном (равнозамедленном) движении (
По определению, мгновенное значение ускорения определяется выражением:
,
ĸᴏᴛᴏᴩᴏᴇ представим в виде: . Интегрируем это уравнение и получаем: , где . Найдем ее значение. Предположим, что в начальный момент времени скорость тела была равной . Подстановка этого условия в полученное выражение для скорости движения тела приводит к соотношению По этой причине имеем:
.
Стоит сказать, что для нахождения зависимости пройденного телом пути от времени воспользуемся определением мгновенной скорости: и полученной зависимостью ее от времени в условиях неизменности величины ускорения. Так как ,имеем: , где .
Как и ранее, определим постоянную интегрирования через начальные условия. В случае если в начальный момент времени координата тела была равной , то получаем: и зависимость координаты тела от времени принимает вид:
.
Читайте также
Ускорение характеризует темп изменения скорости. Как и ранее, вводится понятие среднего ускорения и в случае имеем величину, характеризующую мгновенное ускорение: . Размерность ускорения . Соответствующие компоненты ускорения в Декартовой системе координат могут… [читать подробенее]
Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Пусть в некоторый момент времени движущаяся точка находится в положении и имеет скорость , а в момент приходит в положение и имеет скорость… [читать подробенее]
Вектор скорости точки Лекция 8 Скоростью называется векторная величина, модуль которой определяется изменением пройденного пути за единицу времени. Скорость будем обозначать символом , а ее модуль – , тогда: ; . Рис.8.1. Так как скорость – вектор, то кроме… [читать подробенее]
Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости. Пусть в некоторый момент времени движущаяся точка находится в положении и имеет скорость (рис.2.4), а в момент времени приходит в точку и имеет … [читать подробенее]
Вектор скорости В общем случае движения тела неравномерно. Скорость точки меняется. Поэтому вводят понятие средней скорости как величины равной длине пути, пройденной телом за некоторый промежуток времени . Различия в скоростях в моменты времени и будут тем меньше,… [читать подробенее]
oplib.ru
Ускорение – это… Что такое Ускорение?
Падающий мяч при отсутствии сопротивления воздуха ускоряется, то есть движется все быстрее и быстрее.Ускоре́ние (обычно обозначается , в теоретической механике ) — производная скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости точки (тела) при её (его) движении за единицу времени (то есть ускорение учитывает не только изменение величины скорости, но и её направления).
Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².
Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду (m/s2, м/с2), существует также внесистемная единица Гал (Gal), применяемая в гравиметрии и равная 1 см/с2.
Производная ускорения по времени, то есть величина, характеризующая скорость изменения ускорения, называется рывок:
- , где: — вектор рывка.
Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости материальной точки по времени:
- .
Ускорение точки при прямолинейном движении
Если вектор не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:
- .
Из вышеприведённых двух формул можно вывести ещё одну, связывающую скалярные величины:
Здесь — начальная скорость тела, — конечная скорость тела; — ускорение тела; — пройденный телом путь.
Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным.
Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное, вообще говоря, не верно).
Ускорение точки при движении по окружности
Вектор ускорения
при движении точки по окружности можно разложить на два слагаемых (компоненты):
Тангенциальное ускорение — направлено по касательной к траектории (обозначается иногда и т. д., в зависимости от того, какой буквой в данной книге принято обозначать ускорение). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.
Центростремительное или Нормальное ускорение — возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) (также обозначается иногда и т. д.). Является составляющей вектора ускорения a, перпендикулярной вектору мгновенной скорости. Характеризует изменение скорости по направлению. Вектор нормального ускорения всегда направлен к центру окружности, а модуль равен:
Угловое ускорение — показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:
Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растёт, и наоборот.
Ускорение точки при движении по кривой
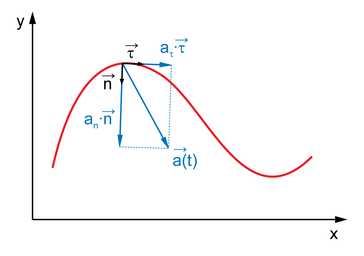
Вектор ускорения можно разложить по сопутствующему базису :
- ,
где
, называемое бинормальным ускорением, всегда равно нулю. Это можно считать прямым следствием определения векторов : можно сказать, что они выбираются именно так, чтобы первый всегда совпадал с нормальным ускорением, второй же ортогонально первому.
Векторы и называются касательным (тангенциальным) и нормальным ускорениями соответственно.
Итак, учитывая сказанное выше, вектор ускорения всегда можно записать как:
- ,
Ускорения в твёрдом теле
Связь ускорений двух точек можно получить, продифференцировав формулу Эйлера для скоростей по времени:
- ,
где — вектор угловой скорости тела, а — вектор углового ускорения тела.
Второе слагаемое называется осестремительным ускорением.
Ускорение при сложном движении
Говорят, что материальная точка (тело) совершает сложное движение, если она движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. Тогда абсолютное ускорение тела равно сумме относительного, переносного и кориолисова:
- .
Первый закон Ньютона постулирует существование инерциальных систем отсчёта. В этих системах отсчёта равномерное прямолинейное движение имеет место в том случае, когда тело (материальная точка) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом, постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчёта всегда является некоторое внешнее силовое воздействие.
Второй закон Ньютона утверждает, что ускорение материальной точки всегда пропорционально приложенной к ней и порождающей ускорение силе, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется массой материальной точки):
Единицы измерения ускорения
- метр на секунду в квадрате (метр в секунду за секунду), м/с², производная единица системы СИ
- сантиметр на секунду в квадрате (сантиметр в секунду за секунду), см/с², производная единица системы СГС
| м/с2 | фут/с2 | g0 | см/с2 | |
|---|---|---|---|---|
| 1 м/с2 = | 1 | 3.28084 | 0.101972 | 100 |
| 1 фут/с2 = | 0.304800 | 1 | 0.0310810 | 30.4800 |
| 1 g0 = | 9.80665 | 32.1740 | 1 | 980.665 |
| 1 см/с2 = | 0.01 | 0.0328084 | 0.00101972 | 1 |
Измерение ускорения
Приборы для измерения ускорения называются акселерометрами. Они не измеряют ускорение непосредственно, а измеряют силу реакции (укр.)русск. опоры, которая возникает при ускоренном движении. Поскольку аналогичные силы сопротивления возникают также и в поле тяготения, то с помощью акселерометров можно измерять также и гравитацию.
Акселерографы — приборы, измеряющие и автоматически записывающие (в виде графиков) значения ускорения поступательного и вращательного движения.
Примеры ускорений
Значения ускорений различных движений:[1]
Примечание: g ≈ 9,81 м/с2.
См. также
Примечания
- ↑ Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике. — 10-е, испр. и доп.. — М.: Наука, 1988. — С. 61. — 256 с. — ISBN 5-02-013833-9
Ссылки
- Ландау, Л. Д., Лифшиц, Е. М. Механика. — Издание 5-е, стереотипное. — М.: Физматлит, 2004. — 224 с. — («Теоретическая физика», том I). — ISBN 5-9221-0055-6
dik.academic.ru
Ускорение – это… Что такое Ускорение?
Падающий мяч при отсутствии сопротивления воздуха ускоряется, то есть движется все быстрее и быстрее.Ускоре́ние (обычно обозначается , в теоретической механике ) — производная скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости точки (тела) при её (его) движении за единицу времени (то есть ускорение учитывает не только изменение величины скорости, но и её направления).
Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².
Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду (m/s2, м/с2), существует также внесистемная единица Гал (Gal), применяемая в гравиметрии и равная 1 см/с2.
Производная ускорения по времени, то есть величина, характеризующая скорость изменения ускорения, называется рывок:
- , где: — вектор рывка.
Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости материальной точки по времени:
- .
Ускорение точки при прямолинейном движении
Если вектор не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:
- .
Из вышеприведённых двух формул можно вывести ещё одну, связывающую скалярные величины:
Здесь — начальная скорость тела, — конечная скорость тела; — ускорение тела; — пройденный телом путь.
Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным.
Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное, вообще говоря, не верно).
Ускорение точки при движении по окружности
Вектор ускорения
при движении точки по окружности можно разложить на два слагаемых (компоненты):
Тангенциальное ускорение — направлено по касательной к траектории (обозначается иногда и т. д., в зависимости от того, какой буквой в данной книге принято обозначать ускорение). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.
Центростремительное или Нормальное ускорение — возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) (также обозначается иногда и т. д.). Является составляющей вектора ускорения a, перпендикулярной вектору мгновенной скорости. Характеризует изменение скорости по направлению. Вектор нормального ускорения всегда направлен к центру окружности, а модуль равен:
Угловое ускорение — показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:
Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растёт, и наоборот.
Ускорение точки при движении по кривой
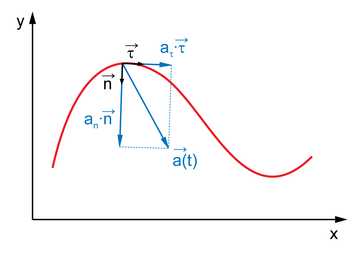
Вектор ускорения можно разложить по сопутствующему базису :
- ,
где
, называемое бинормальным ускорением, всегда равно нулю. Это можно считать прямым следствием определения векторов : можно сказать, что они выбираются именно так, чтобы первый всегда совпадал с нормальным ускорением, второй же ортогонально первому.
Векторы и называются касательным (тангенциальным) и нормальным ускорениями соответственно.
Итак, учитывая сказанное выше, вектор ускорения всегда можно записать как:
- ,
Ускорения в твёрдом теле
Связь ускорений двух точек можно получить, продифференцировав формулу Эйлера для скоростей по времени:
- ,
где — вектор угловой скорости тела, а — вектор углового ускорения тела.
Второе слагаемое называется осестремительным ускорением.
Ускорение при сложном движении
Говорят, что материальная точка (тело) совершает сложное движение, если она движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. Тогда абсолютное ускорение тела равно сумме относительного, переносного и кориолисова:
- .
Первый закон Ньютона постулирует существование инерциальных систем отсчёта. В этих системах отсчёта равномерное прямолинейное движение имеет место в том случае, когда тело (материальная точка) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом, постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчёта всегда является некоторое внешнее силовое воздействие.
Второй закон Ньютона утверждает, что ускорение материальной точки всегда пропорционально приложенной к ней и порождающей ускорение силе, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется массой материальной точки):
Единицы измерения ускорения
- метр на секунду в квадрате (метр в секунду за секунду), м/с², производная единица системы СИ
- сантиметр на секунду в квадрате (сантиметр в секунду за секунду), см/с², производная единица системы СГС
| м/с2 | фут/с2 | g0 | см/с2 | |
|---|---|---|---|---|
| 1 м/с2 = | 1 | 3.28084 | 0.101972 | 100 |
| 1 фут/с2 = | 0.304800 | 1 | 0.0310810 | 30.4800 |
| 1 g0 = | 9.80665 | 32.1740 | 1 | 980.665 |
| 1 см/с2 = | 0.01 | 0.0328084 | 0.00101972 | 1 |
Измерение ускорения
Приборы для измерения ускорения называются акселерометрами. Они не измеряют ускорение непосредственно, а измеряют силу реакции (укр.)русск. опоры, которая возникает при ускоренном движении. Поскольку аналогичные силы сопротивления возникают также и в поле тяготения, то с помощью акселерометров можно измерять также и гравитацию.
Акселерографы — приборы, измеряющие и автоматически записывающие (в виде графиков) значения ускорения поступательного и вращательного движения.
Примеры ускорений
Значения ускорений различных движений:[1]
Примечание: g ≈ 9,81 м/с2.
См. также
Примечания
- ↑ Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике. — 10-е, испр. и доп.. — М.: Наука, 1988. — С. 61. — 256 с. — ISBN 5-02-013833-9
Ссылки
- Ландау, Л. Д., Лифшиц, Е. М. Механика. — Издание 5-е, стереотипное. — М.: Физматлит, 2004. — 224 с. — («Теоретическая физика», том I). — ISBN 5-9221-0055-6
3dic.academic.ru



