В чем измеряется ускорение в физике – Единицы измерения укорения (линейного). Перевод единиц измерения ускорения – таблица. Ускорение свободного падения g во всех единицах измерения.
- Комментариев к записи В чем измеряется ускорение в физике – Единицы измерения укорения (линейного). Перевод единиц измерения ускорения – таблица. Ускорение свободного падения g во всех единицах измерения. нет
- Советы абитуриенту
В чём измеряется ускорение? – Полезная информация для всех
Ускорением правильно считать производную скорости, взятую по времени.
Ускорение – это векторная переменная, которая показывает изменение величины скорости тела за единицу времени.
В системе измерения СИ – ускорение измеряется в метрах на секунду в квадрате, м/с2 (m/s). А также ускорение редко и преимущественно в гравиметрии, измеряется в Галомах (Gal). В свою очередь один Галом равняется 1 сантиметру на секунду в квадрате, см/с.

Ускорение измеряется в метрах в секунду за секунду, а также в метрах на секунду в квадрате.
В физике ускорением называют величину, характеризующую быстроту изменения скорости, равную отношению изменения скорости тела к временному промежутку, в течение которого это изменение и произошло.
Ускорение – это величина которая дает представление о том, как быстро изменяется скорость тела со временем, поэтому эта величина равна нулю, для тел движущихся с постоянной скоростью. В СИ нет специальной единицы для измерения ускорения и ее обозначают просто как метр на секунду в квадрате:
Чтобы понять эту размерность надо вспомнить определение ускорения и разбить размерность на составляющие: М/С – это скорость, и домножение на 1/С – ее изменение за секунду.
В СГС единицей ускорения является ГАЛ, величина, названная в честь изучавшего ускорение свободного падения итальянца Галилея, который для этого сбрасывал шарики с Пизанской башни.
Ускорение – это изменение скорости: например,
автомобиль с места набрал скорость 50км/час за 10 секунд.
Переведем 50км/час = 50 000м/3600с = 7,94м/с
Тогда ускорение составит 7,94/10 = 0,794 м/с2
Ускорение измеряется в метрах в секунду в квадрате.
Ускорение играет немаловажную роль для того чтобы определить силу, импульс и т.д.
Ускорение связано как все догадываются со скоростью.
Скорость связано со временем .
Вот и находим что a- ускорение измеряется в Скорости деленной на время.
V/с*с= а.
Метр/секунда в квадрате. Помню до дыр заучивали это в школе по математике. Не сказать что помогло, но однажды очень даже пригодилось. Тут как говорится нужно математиком быть. В противном случае для незнающих математики эти цифры – пустой звук. По крайней мере мне так кажется.
Ускорение измеряется в метр/секунда в квадрате
Это я хорошо запомнил еще со школьной программы ибо очень уж забавная величина, точнее звучит она забавно 🙂 Итак, ускорение принято измерять в метрах в секунду за секунду. Ускорение – это физическая величина. Вот и вс, по моему такое своеобразное название достаточно легко запомнить, если постараться.
На уроках физики много лет назад я узнал, что ускорение измеряется в м/с.
Ускорение показывает отношение изменения скорости движения тела ко времени данного изменения.
Тело, которое под действием силы тяжести падает на землю, движется с ускорением свободного падения, равным 9,8 м/с.
Кроме системной единицы измерения есть ещ и внесистемная: gal, которая применяется в гравиметрии. 1 gal = 980,6 см/с.
Если вспомнить школьную программу, то мы можем сказать, что ускорение показывает нам изменение скорости движения предмета во времени. А мы знаем, что скорость измеряется в м/с (расстояние на время), а значит, ускорение измеряется в м/с^2. Это в системе СИ.
Также существует и внесистемная единица измерения ускорения, называемая гал (1см/с^2).
Метры деленные на секунду в квадрате,это я знаю из школьного курса)
Еще со школьной программы мы все знаем, что ускорение измеряется в метрах/секунда в квадрате. Именно эта единица измерения принята международной системой измерения СИ. Это проходят, если не ошибаюсь, на уроках физики шестого класса.
info-4all.ru
Ускорение — Циклопедия
Ускорение — физическая векторная величина, которая характеризует насколько быстро тело (материальная точка) изменяет скорость своего движения. Ускорение является важной кинематической характеристикой материальной точки.
[править] Среднее и мгновенное ускорение
Среднее ускорение материальной точки на некотором промежутке времени — это отношение изменения его скорости, что произошло за это время, к продолжительности этого промежутка:
[math]\lt\vec a\gt = \frac {\Delta \vec v} {\Delta t}[/math]
Мгновенное ускорение материальной точки в некоторый момент времени — это лимит его среднего ускорения при [math]\Delta t \to 0[/math]. Имея в виду определение производной функции, мгновенное ускорение можно определить как производную от скорости по времени:
[math]\vec a = \frac {d\vec v} {dt}[/math]
[править] Тангенциальное и нормальное ускорение
Если записать скорость как [math]\vec v = v\hat \tau[/math], где [math]\hat \tau[/math] — орт касательной к траектории движения, то (в двухмерной системе координат):
[math]\vec a = \frac {d(v\hat \tau)} {dt} = \frac {dv} {dt} \hat \tau + \frac {d\hat \tau} {dt} v = \frac {dv} {dt} \hat \tau + \frac {d(\cos\theta\vec i + sin\theta \vec j)} {dt} v = \frac {dv} {dt} \hat \tau + (-sin\theta \frac {d\theta} {dt} \vec i + cos\theta \frac {d\theta} {dt} \vec j)) v = \frac {dv} {dt} \hat \tau + \frac {d\theta} {dt} v \hat n[/math],
где [math]\theta[/math] — угол между вектором скорости и осью абсцисс; [math]\hat n[/math] — орт перпендикуляра к скорости.
Таким образом,
[math]\vec a = \vec a_{\tau} + \vec a_n[/math],
где [math]\vec a_{\tau} = \frac {dv} {dt} \hat \tau[/math] — тангенциальное ускорение, [math]\vec a_n = \frac {d\theta} {dt} v \hat n[/math] — нормальное ускорение.
Учитывая, что вектор скорости направлен по касательной к траектории движения, то [math]\hat n[/math] — это орт нормали к траектории движения, который направлен к центру кривизны траектории. Таким образом, нормальное ускорение направлено к центру кривизны траектории, в то время как тангенциальное — по касательной к ней. Тангенциальное ускорение характеризует скорость изменения величины скорости, в то время как нормальное характеризует скорость изменения ее направления.
Движение по криволинейной траектории в каждый момент времени можно представить как вращение вокруг центра кривизны траектории с угловой скоростью [math]\omega = \frac v r[/math], где r — радиус кривизны траектории. В таком случае
[math]a_{n} = \omega v = {\omega}^2 r = \frac {v^2} r[/math]
[править] Измерение ускорения
Ускорение измеряется в метрах (разделенных) на секунду во второй степени (м/с2). Величина ускорения определяет, насколько изменится скорость тела за единицу времени, если оно будет постоянно двигаться с таким ускорением. Например, тело, движущееся с ускорением 1 м/с2 за каждую секунду изменяет свою скорость на 1 м/с.
[править] Единицы измерения ускорения
cyclowiki.org
Ускорение, как физическая величина
Когда тело движется, его скорость меняется как по модулю, так и по направлению.
Меняется скорость поезда, сначала увеличивается, затем постоянна, и, в конце движения пути, уменьшается. Пуля, вылетающая из ствола, увеличивает скорость, при попадании в цель, ее скорость уменьшается. Здесь скорость изменяется практически мгновенно. Изменяется скорость мяча во время игры в футбол, как по величине, так и направлению, и автомобиля, двигающегося на повороте.
Быстроту изменения скорости за какой-то промежуток времени характеризуют величиной называемой ускорением.
Ввел понятие ускорения Галилей, изучая связь между падением тел и силой тяжести. Ускорение, как и скорость, имеет направление.
Среднее ускорение
Рассмотрим криволинейное неравномерное движение. Ускорение будет иметь разное значение и направление. В этом случае находят среднее ускорение. Равно ускорение отношению (изменению вектора), за промежуток времени, в течение которого это изменение происходило.
Определяется по формуле
Разность начального значения v и значения v через промежуток времени или изменение вектора скорости измеряется в метрах в секунду (м/с).
Промежуток времени , во время этого промежутка происходило изменение ускорения, измеряется в секундах (с)
Ускорение а, измеряется оно в метрах м/с2 в системе СИ (За 1с скорость тела успевает измениться на 1 м\с).
Мгновенное ускорение
Если промежуток времени стремится неограниченно к нулю , находят ускорение в данной точке, называемое мгновенным.
Мгновенное ускорение равно:
Рассмотрим простой вид движения — прямолинейное движение. Направление скорости не изменяется, . Модуль скорости увеличивается, движение будет равноускоренным. Скорость и ускорение сонаправлены, совпадают по направлению. Модуль скорости убывает – движение равнозамедленное, скорость и ускорение направлены в этом случае противоположно друг другу (торможение автобуса).
При изменении направления ускорения и скорости при движении, если модуль ускорения , направление его не меняется, движение называется равнопеременным (движение брошенного вверх камня).
Нормальное и тангенциальное ускорение
Рассмотрим криволинейное движение. Скорость тела направлена по касательной к траектории. Ускорение в данном случае можно разложить на две составляющие.
Одна составляющая ускорения направлена по касательной, так же как вектор скорости, называется тангенциальным ускорением. Другая направлена в центр окружности. Это ускорение называется центростремительным или нормальным ускорением («стремящимся к центру»). Исходя из теоремы Пифагора, можно определить ускорение:
Центростремительное ускорение
Упростим криволинейное движение, представив его как движение по дугам концентрических окружностей.
Рассмотрим движение по окружности. Скорость меняется по направлению.
Величина скорости остается постоянной.
Тангенциальное ускорение равно нулю, а нормальное или центростремительное можно определить по формуле: .
v- скорость тела.
R – радиус окружности, по которой движется тело, измеряется в системе СИ в метрах (м).
fizikatyt.ru
В чем измеряется ускорение — что такое ускорение? ? по физике — 22 ответа
В чём измеряется ускорение тела
В разделе Техника на вопрос что такое ускорение? ? по физике заданный автором хромосомы лучший ответ это Ускоре́ние — производная скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости точки (тела) при её (его) движении за единицу времени (то есть ускорение учитывает не только изменение величины скорости, но и её направления).
Ответ от 22 ответа[гуру]Привет! Вот подборка тем с ответами на Ваш вопрос: что такое ускорение? ? по физике
Ответ от Tigraroma[гуру]
Ускорение (в русскоязычной литературе обычно обозначается a) — векторная величина, характеризующая быстроту изменения скорости тела.
Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с^2. (Замечание: в большинстве школьных задач по физике можно считать ускорение свободного падения равным 10 м/с^2.)
Быстрота изменения ускорения в физике носит название комфортабельность.
Ускорение тела в механике
Вектор ускорения в любой момент времени находится путём дифференцирования вектора скорости частицы по времени: w = dv / dt
Вектор ускорения w можно представить в виде
w = w_t + w_n = dv / dt + v^2 * n
где
* v – величина скорости
* t – единичный касательный к траектории вектор, направленный вдоль скорости (касательный орт) ,
* n – единичный вектор нормали к траектории,
* R – радиус кривизны траектории.
Векторы w_t и w_n называются касательным и нормальным ускорениями соответственно.
Единицы измерения ускорения
* метр в секунду в квадрате, м/с^2, производная единица системы СИ
* сантиметр в секунду в квадрате, cм/с^2, производная единица системы СГС
Ответ от Европейский[гуру]
Это движение, которое совершается под воздействием силы. Когда к движущемуся предмету постоянно преложена сила, а другие силы не действуют или находятся в равновесии. Вы должны понять, что толчок – не преложенная сила. Сила должна как бы чувствоваться постоянно. Представьте, что вы хоть и двигаетесь, но вас толкают с одной и той же силой. Вы будете двигаться все быстрее и быстрее, пока сила не прекратится.
Ответ от Александр Клементьев[гуру]
Чтобы было понятнее, скорость изменения скорости. Или функция скорости во времени.
Ответ от Прострелить[гуру]
Величина, численно равная изменению скорости тела в единицу времени.
Ответ от Иван шкинёв[новичек]
Нет, ребята! Ускорение-это не прибавка “скорости к скорости”! Ускорение-это энергия движения. Она есть и в постоянном движении и, даже, в замедляющемся движении. Что меняет, если начальная скорость больше конечной, или скорости равны? Есть одна, основная-СРЕДНЯЯ-скорость. ОТ неё надо “плясать”! Кстати, при свободном падении (на Земле) ускорение не 9,8,а 4,9 м/сек. сек. 9,8-это скорость в конце первой секунды падения. Есть v начальное, v-конечное, и средняя скорость-at. Если начальная скорость при свободном падении равна 0, то конечная скорость будет 2at. И формула будет s=2att/2 (площадь треугольника). Все расчёты по механике на мощность, разгон, КПД…. надо забыть. Пока за основу расчётов не будете брать СРЕДНЮЮ скорость при движении. Пример: какая мощность мотора Вашего автомобиля, если известна масса его и время разгона до 100 км/час? f=ma m=1170 кг. t=18 сек. v конеч. =27,7 м/сек. a=v/t v- СРЕДНЯЯ- =13,9 м. /сек. a=13,9:18=0,77 f=1170 х 0,77=903 кг. м. Это 12 л. с. А мотор ваших “Жигулей”-75 л. с. Это-5625 кг. м. КПД-16 % У всех машин!
Вот упрощенная формула для автомобилей: 12N=ma N-в “лошадиных силах” сразу, чтобы не переводить кг. м. в л. с. (Жигули….) 12*75=1170*a a=0,77 м/сек. сек Время разгона до сотни- 13,9:0,77=18 секунд. (проверь-те на своей машине… И КПД и мощность..)
Теперь можно узнать, какую мощность надо при езде по асфальту, грунтовке, или по бездорожью… И какой будет расход топлива!
Ответ от тима масаев[новичек]
мне балл пожалуйста
Ответ от Айна мальсагова[новичек]
для описания движения тел с изменяющейся скоростью необходима физическая величина характеризуюшая процесс изменения скорости с течением времени
Ответ от DOJE[новичек]
мне бал тоже
Ответ от ASHAT AVZHANOV[новичек]
и
Ответ от Алина Юсупова[новичек]
Ускорение-это физическая величена, определяющая быстрому изменения скорости тела, то есть первая производная от скорости по времени.
Ускорение на Википедии
Посмотрите статью на википедии про Ускорение
22oa.ru
Ускорение | Наука | FANDOM powered by Wikia
Если движение точки прямолинейно, можно построить график зависимости скорости от времени. При этом величина ускорения будет равна тангенсу угла наклона касательной к графику в указанной точке.
Ускоре́ние (обычно обозначается $ \vec a $, в теоретической механике $ \vec w $), производная скорости по времени — векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления).
Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².
Раздел механики, изучающий движение в трёхмерном евклидовом пространстве, его запись, а также запись скоростей и ускорений в различных системах отсчёта, называется кинематикой.
Единицей ускорения служит метр в секунду за секунду (m/s2, м/с2), существует также внесистемная единица Гал (Gal), применяемая в гравиметрии и равная 1 см/с
Производная ускорения по времени т.е. величина, характеризующая быстроту изменения ускорения по времени называется рывок.
Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости материальной точки по времени:
- $ \vec a = {d\vec v \over dt} = {d^2\vec r \over dt^2} $.
Ускорение точки при прямолинейном движении Править
Если вектор $ \vec a $ не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:
- $ \vec v(t) = \vec v_0 + (t – t_0)\vec a $
- $ \vec r(t) = \vec r_0 + (t-t_0)\vec v_0 + {(t-t_0)^2\over 2}\vec a $.
Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным.
Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное, вообще говоря, не верно)
Ускорение точки при движении по окружности Править
w = wτ + wn
Тангенциальное ускорение — направлено по касательной к траектории, обозначается wτ (aτ). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.
- $ \begin{alignat}{3} \mathbf{a} & = \frac{d \mathbf{v}}{dt} \\ \end{alignat} $
Центростремительное или Нормальное ускорение — возникает при движении точки по окружности, обозначается wn. Является составляющей вектора ускорения w. Вектор нормального ускорения всегда направлен к центру окружности, а модуль равен:
- $ |\vec a| = \omega ^2 r = {v^2 \over r} $
Угловое ускорение — показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:
- $ \vec \varepsilon = {d\vec \omega \over dt} $
Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растёт, и наоборот.
Ускорение точки при движении по кривой Править
Разложение ускорения по сопутствующему базису для движения в плоскости
Вектор ускорения $ \vec a $ можно разложить по сопутствующему базису $ \left\{\vec \tau, \vec{n}, \vec{b}\right\} $:
- $ \vec a = {a}_\tau {\vec \tau} + {a}_n {\vec n} + {a}_b {\vec b} = \frac{dv}{dt}{\vec \tau} + \frac{v^2}{R} {\vec n} + {a}_b {\vec b} $,
где
- $ v $ — величина скорости,
- $ {\vec \tau} $ — единичный касательный к траектории вектор, направленный вдоль скорости (касательный орт),
- $ {\vec n} $ — орт нормали к траектории,
- $ {\vec b} $ — орт бинормали к траектории,
- $ R $ — радиус кривизны траектории.
Известно, что $ {a}_b{\vec b} $, называемое бинормальным ускорением, всегда равно нулю.
Векторы $ {a}_\tau{\vec \tau} $ и $ {a}_n{\vec n} $ называются касательным (тангенциальным) и нормальным ускорениями соответственно.
Ускорения в твёрдом теле Править
Связь ускорений двух точек можно получить, продифференцировав формулу Эйлера для скоростей по времени:
- $ \vec{w}_B = \vec{w}_A + \left[\vec{\omega}, \left[ \vec{\omega}, \vec{AB}\right] \right] + \left[ \varepsilon, \vec{AB} \right] $,
где $ \vec{\omega} $ — вектор угловой скорости тела, а $ \vec{\varepsilon} $ — вектор углового ускорения тела.
Второе слагаемое называется осестремительным ускорением.
Ускорение при сложном движении Править
Абсолютное ускорение равно сумме относительного, переносного и кориолисова:
- $ \vec a_a=\vec {a}_r + \vec {a}_e + 2\left[\vec \omega \times \vec {v}_r \right] $.
Первый закон Ньютона постулирует существование инерциальных систем отсчета. В этих системах отсчета равномерное прямолинейное движение имеет место всякий раз, когда тело (материальная точка) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчета всегда является некоторое внешнее силовое воздействие.
Второй закон Ньютона утверждает, что приложенная (к точке) сила и порождаемое ей ускорение точки всегда пропорциональны, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется массой материальной точки):
- $ \vec F = m\vec a $.
Единицы измерения ускорения Править
ru.science.wikia.com
Ускорение – это… Что такое Ускорение?
Падающий мяч при отсутствии сопротивления воздуха ускоряется, то есть движется все быстрее и быстрее.Ускоре́ние (обычно обозначается , в теоретической механике ) — производная скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости точки (тела) при её (его) движении за единицу времени (то есть ускорение учитывает не только изменение величины скорости, но и её направления).
Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².
Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду (m/s2, м/с2), существует также внесистемная единица Гал (Gal), применяемая в гравиметрии и равная 1 см/с2.
Производная ускорения по времени, то есть величина, характеризующая скорость изменения ускорения, называется рывок:
- , где: — вектор рывка.
Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости материальной точки по времени:
- .
Ускорение точки при прямолинейном движении
Если вектор не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:
- .
Из вышеприведённых двух формул можно вывести ещё одну, связывающую скалярные величины:
Здесь — начальная скорость тела, — конечная скорость тела; — ускорение тела; — пройденный телом путь.
Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным.
Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное, вообще говоря, не верно).
Ускорение точки при движении по окружности
Вектор ускорения
при движении точки по окружности можно разложить на два слагаемых (компоненты):
Тангенциальное ускорение — направлено по касательной к траектории (обозначается иногда и т. д., в зависимости от того, какой буквой в данной книге принято обозначать ускорение). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.
Центростремительное или Нормальное ускорение — возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) (также обозначается иногда и т. д.). Является составляющей вектора ускорения a, перпендикулярной вектору мгновенной скорости. Характеризует изменение скорости по направлению. Вектор нормального ускорения всегда направлен к центру окружности, а модуль равен:
Угловое ускорение — показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:
Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растёт, и наоборот.
Ускорение точки при движении по кривой
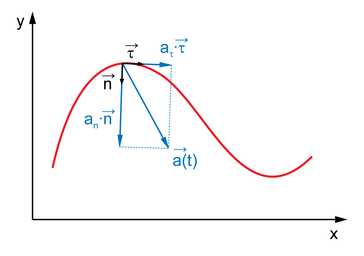
Вектор ускорения можно разложить по сопутствующему базису :
- ,
где
, называемое бинормальным ускорением, всегда равно нулю. Это можно считать прямым следствием определения векторов : можно сказать, что они выбираются именно так, чтобы первый всегда совпадал с нормальным ускорением, второй же ортогонально первому.
Векторы и называются касательным (тангенциальным) и нормальным ускорениями соответственно.
Итак, учитывая сказанное выше, вектор ускорения всегда можно записать как:
- ,
Ускорения в твёрдом теле
Связь ускорений двух точек можно получить, продифференцировав формулу Эйлера для скоростей по времени:
- ,
где — вектор угловой скорости тела, а — вектор углового ускорения тела.
Второе слагаемое называется осестремительным ускорением.
Ускорение при сложном движении
Говорят, что материальная точка (тело) совершает сложное движение, если она движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. Тогда абсолютное ускорение тела равно сумме относительного, переносного и кориолисова:
- .
Первый закон Ньютона постулирует существование инерциальных систем отсчёта. В этих системах отсчёта равномерное прямолинейное движение имеет место в том случае, когда тело (материальная точка) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом, постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчёта всегда является некоторое внешнее силовое воздействие.
Второй закон Ньютона утверждает, что ускорение материальной точки всегда пропорционально приложенной к ней и порождающей ускорение силе, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется массой материальной точки):
Единицы измерения ускорения
- метр на секунду в квадрате (метр в секунду за секунду), м/с², производная единица системы СИ
- сантиметр на секунду в квадрате (сантиметр в секунду за секунду), см/с², производная единица системы СГС
| м/с2 | фут/с2 | g0 | см/с2 | |
|---|---|---|---|---|
| 1 м/с2 = | 1 | 3.28084 | 0.101972 | 100 |
| 1 фут/с2 = | 0.304800 | 1 | 0.0310810 | 30.4800 |
| 1 g0 = | 9.80665 | 32.1740 | 1 | 980.665 |
| 1 см/с2 = | 0.01 | 0.0328084 | 0.00101972 | 1 |
Измерение ускорения
Приборы для измерения ускорения называются акселерометрами. Они не измеряют ускорение непосредственно, а измеряют силу реакции (укр.)русск. опоры, которая возникает при ускоренном движении. Поскольку аналогичные силы сопротивления возникают также и в поле тяготения, то с помощью акселерометров можно измерять также и гравитацию.
Акселерографы — приборы, измеряющие и автоматически записывающие (в виде графиков) значения ускорения поступательного и вращательного движения.
Примеры ускорений
Значения ускорений различных движений:[1]
Примечание: g ≈ 9,81 м/с2.
См. также
Примечания
- ↑ Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике. — 10-е, испр. и доп.. — М.: Наука, 1988. — С. 61. — 256 с. — ISBN 5-02-013833-9
Ссылки
- Ландау, Л. Д., Лифшиц, Е. М. Механика. — Издание 5-е, стереотипное. — М.: Физматлит, 2004. — 224 с. — («Теоретическая физика», том I). — ISBN 5-9221-0055-6
dvc.academic.ru



