Задачи на погрешность по метрологии – “Решение задач на определение погрешностей эксперимента.”. Скачать бесплатно и без регистрации.
- Комментариев к записи Задачи на погрешность по метрологии – “Решение задач на определение погрешностей эксперимента.”. Скачать бесплатно и без регистрации. нет
- Советы абитуриенту
- Погрешности измерений – Ответы на вопросы по метрологии
- 1.1. Погрешности в метрологии
- Расчет допусков и посадок подшипникового соединения. Пример решения задачи.
- Информатики и радиоэлектроники
- Задачи по метрологии Задача 11
- Решение типовых задач метрологии – n1.doc
- Сборник задач по расчету погрешностей электрических измерений
Погрешности измерений – Ответы на вопросы по метрологии
Погрешность измерения – это отклонение результата измерения от истинного значения величины.
Истинное значение – это значение физической величины, которое идеальным образом отражало бы в качественном и количественном отношениях соответствующие свойства объекта.
Точность измерения – качество измерений, отражающее близость к нулю систематических погрешностей результатов.
Достоверность измерений – степень доверия к результатам измерений.
Сходимость измерений – качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в одинаковых условиях.
Воспроизводимость измерений – качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в различных условиях.
Результат измерений всегда имеет погрешность.
По способу выражения погрешности подразделяются:
– абсолютная (∆А) – разность между результатом измерений Аизм и действительным значением измеряемой величины Адейст
∆А = Аизм – Адейст
– относительная (δА) – это отношение абсолютной погрешности к действительному значению измеряемой величины
δА = ∆А/Аизм ≈ ∆А/Адейст
По условиям измерений погрешности подразделяются:
– основные, возникающие при измерениях произведенных при условиях, принятых за нормальные: температура +20±5 ºС, относительная влажность 65±15 %, давление 100000±4000 Па;
– дополнительные, возникающие при измерениях произведенных при условиях, отличных от нормальных.
По характеру проявления погрешности подразделяются:
– систематические, остающиеся постоянными (или закономерно изменяющиеся) при повторных измерениях тем же способом и средствами;
– случайные, изменяющиеся случайным образом при повторных измерениях одной и той же величины.
ПРОМАХИ – это грубые ошибки, обусловленные неправильным отсчетом или расчетом, небрежностью измеряющего и т.п., которые в ряде измерений не учитываются. Для суждения о том, можно ли отнести какой-то результат измерений к промахам, часто применяют правило «трех сигм». Под величиной сигма (σ) понимается среднее квадратическое отклонение случайной величины Аn от ее среднего значения Аср:
σ = ±(1/√n-1)* √(А1-Аср)2 + (А2-Аср)2 + (А3-Аср)2 +…+ (Аn-Аср)2
Результат измерений, отклоняющийся от Аср больше чем на 3 σ, обычно считают промахом.
ОСНОВНАЯ погрешность для измерительных приборов определяется их классом точности (К), который указывается на шкале или в паспорте прибора. У приборов с односторонней шкалой за норму принимается отсчет при отклонении стрелки на всю шкалу, называемый номинальным (Аном):
К = 100 ∆Апред/Аном
Электроизмерительные приборы изготавливаются девяти классов точности: 0,02; 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0.
Относительная погрешность результата измерения δизм в данном случае определяется из соотношения
δизм (%) = (∆Апред/Аном)*100 = (∆Аном/Аизм)*К
Задача 1.3.1 Определить абсолютную и относительную погрешность результатов измерения напряжения в электрической цепи, если действительное значение напряжения равно 220 В, а были получены следующие значения: 221 В; 219 В; 217 В; 256 В; 220 В. Определить были ли промахи в результате измерения. Какой из полученных результатов измерен наиболее точно
Решение:
1 Определяем абсолютную погрешность измерений
∆А = Аизм – Адейст
∆U1 = 221 – 220 = 1 В
∆U2 = 219 – 220 = – 1 В
∆U3 = 217 – 220 = – 3 В
∆U4 = 256 – 220 = 36 В
∆U5 = 220 – 220 = 0 В
2 Определяем относительную погрешность измерений
δА = ∆А/Аизм ≈ ∆А/Адейст
δU1 = 100∆U1/Uизм = 1/221 = 0,8 %
δU2 = 100∆U2/Uизм = 1/219 = 0,4 %
δU3 = 100∆U3/Uизм = 3/217 = 1,3 %
δU4 = 100∆U4/Uизм = 36/256 = 14 %
δU5 = 100∆U5/Uизм = 0/220 = 0 %
3 Определяем были ли промахи в результате проведенных измерений.
3.1 Определяем среднее арифметическое значение результатов измерений
Uср = (U1 + U2 + U3 + U4 + U5)/5
Uср = (221 + 219 + 217 + 256 + 220)/5 = 227 В
3.2 Определяем среднее квадратическое отклонение
σ = ±(1/√n-1)* √(А1-Аср)2 + (А2-Аср)2 + (А3-Аср)2 +…+ (Аn-Аср)2
σ = ±(1/√5-1)*√(221-227)2 +(219-227)2 +(217-227)2+(256-227)2+(220-227)2
σ = ± 2*√ 36 +64 +169+841+49 = ± 68
3*σ = 3* 68 = 204
Ответ: Так как результат измерений не отклоняется от Uср больше чем на 3 σ, то промахов нет.
Задача 1.3.2 Стрелочным вольтметром с равномерной шкалой класса точности К = 1,5 и предельным значением шкалы Uк = 300 В измерены величины трех напряжений 250 В; 150 В; 75 В. Какое из указанных напряжений измерено наиболее точно?
7
Чему равна основная и относительная погрешность каждого измерения?
Построить график изменения величины относительной погрешности заданного прибора в координатах. Дать рекомендации по использованию данного прибора.
Решение:
1 Определяем относительную погрешность каждого измерения
δизм (%) = (∆Uпред/Uном)*100 = (∆Uном/Uизм)*К
δизм 1 = (300/250)*1,5 = 1,8
δизм 2 = (300/150)*1,5 = 3
δизм 3 = (300/75)*1,5 = 6
2 Определяем абсолютную погрешность каждого измерения
δизм (%) = (∆Апред/Аном)*100
∆U = δ Uизм /100
∆U1 = 1,8*250 /100 = 4,5
∆U2 = 3*150 /100 = 4,5
∆U3 = 6*75 /100 = 4,5
Результат первого напряжения U1 = 250 В измерено наиболее точно, так как относительная погрешность его меньше остальных.
Строим график изменения величины относительной погрешности заданного прибора
Рисунок 1.1 – График изменения величины относительной погрешности заданного прибора
Данный вольтметр измеряет показания достаточно близкие к предельному значению шкалы.
МЕТОДИЧЕСКАЯ ПОГРЕШНОСТЬ – это погрешность, возникающая в результате включения измерительных приборов в исследуемую цепь и обусловленная потребляемой ими мощностью.
Методическая погрешность, возникающая при включении амперметра.
Рисунок 1.2 – Схема включения амперметра в электрическую цепь
Iх = U/R – до включения амперметра
Iх = U/(R + RА) – после включения амперметра в цепь
δА = (I – Ix)/Ix = – (RA/R)/(1 + RA/R) – методическая погрешность.
Так как
RA/R = I2 RA/ I2 R = PA/P,
То δА = – PA/P
где РА – мощность, потребляемая амперметром;
Р – мощность, потребляемая исследуемой цепью.
Следовательно, при измерении тока необходимо выбирать приборы, у которых потребляемая мощность значительно меньше мощности, рассеиваемой в исследуемой цепи. Поэтому необходимо, чтобы амперметр обладал как можно меньшим сопротивлением.
Методическая погрешность, возникающая при включении вольтметра.
Uх = I*R = Е*R/(R + R0), – до включения вольтметра
где Е – ЭДС источника тока;
R0 – внутреннее сопротивление источника тока
Рисунок 1.3 – Схема включения вольтметра в электрическую цепь
После включения вольтметра напряжение будет равно
Uх = ЕRRv/(RR0+RvR0+RRv)
Тогда методическая погрешность при включении вольтметра в электрическую цепь равна
δv = (U-Ux)/ Ux = – (R/Rv)/(1+ R/Rv+ R/R0)
Учитывая, что R/Rv = Рv/Р, получаем
δv = – (Рv/Р)/(1+R/R0),
где Рv – мощность, потребляемая вольтметром;
Р – мощность, потребляемая исследуемым резистором.
Следовательно, при измерении напряжения необходимо выбирать приборы, у которых потребляемая мощность значительно меньше мощности, рассеиваемой в исследуемой цепи. Поэтому необходимо, чтобы вольтметр обладал как можно большим сопротивлением.
students-library.com
1.1. Погрешности в метрологии
Ни одно измерение не свободно от погрешностей, или, точнее, вероятность измерения без погрешностей приближается к нулю. Род и причины погрешностей весьма разнообразны и на них влияют многие факторы (рис.1.2).
Общая характеристика влияющих факторов может быть систематизирована с различных точек зрения, например, по влиянию перечисленных факторов (рис.1.2).
По результатам измерения погрешности можно разделить на три вида: систематические, случайные и промахи.
Систематические погрешности, в свою очередь, делят на группы по причине их возникновения и характеру проявления. Они могут быть устранены различными способами, например, введением поправок.
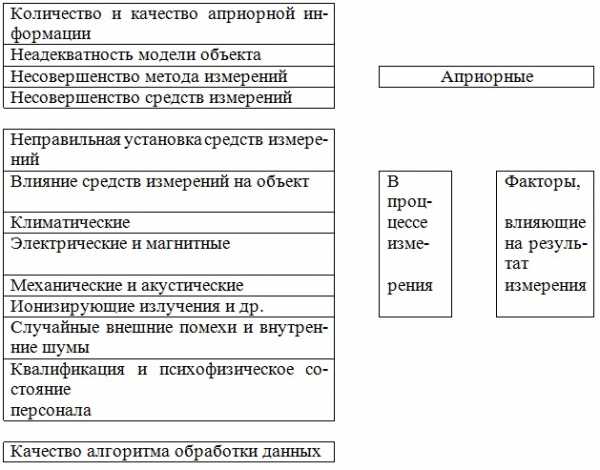
рис. 1.2
Случайные погрешности вызываются сложной совокупностью изменяющихся факторов, обычно неизвестных и трудно поддающихся анализу. Их влияние на результат измерения можно уменьшить, например, путем многократных измерений с дальнейшей статистической обработкой полученных результатов методом теории вероятностей.
К промахам относятся грубые погрешности, которые возникают при внезапных изменениях условия эксперимента. Эти погрешности по своей природе тоже случайны, и после выявления должны быть исключены.
Точность измерений оценивается погрешностями измерений, которые подразделяются по природе возникновения на инструментальную и методическую и по методу вычислений на абсолютную, относительную и приведенную.
Инструментальная погрешность характеризуется классом точности измерительного прибора, который приведен в его паспорте в виде нормируемых основной и дополнительных погрешностей.
Методическая погрешность обусловлена несовершенством методов и средств измерений.
Абсолютная погрешность есть разность между измеренным Guи истинным G значениями величины, определяемая по формуле:
Δ=ΔG=Gu-G
Заметим, что величина имеет размерность измеряемой величины.
Относительную погрешность находят из равенства
δ=±ΔG/Gu·100%
Приведенную погрешность рассчитывают по формуле (класс точности измерительного прибора)
δ=±ΔG/Gнорм·100%
где Gнорм – нормирующее значение измеряемой величины. Ее принимают равной:
а) конечному значению шкалы прибора, если нулевая отметка находится на краю или вне шкалы;
б) сумме конечных значений шкалы без учета знаков, если нулевая отметка расположена внутри шкалы;
в) длине шкалы, если шкала неравномерная.
Класс точности прибора устанавливается при его проверке и является нормируемой погрешностью, вычисляемой по формулам
γ=±ΔG/Gнорм·100%, если ΔGm=const
где ΔGm – наибольшая возможная абсолютная погрешность прибора;
Gk – конечное значение предела измерения прибора; с и d – коэффициенты, учитывающие конструктивные параметры и свойства измерительного механизма прибора.
Например, для вольтметра с постоянной относительной погрешностью имеет место равенство
δm=±c
Относительная и приведенная погрешности связаны следующими зависимостями:
а) для любого значения приведенной погрешности
δ=±γ·Gнорм/Gu
б) для наибольшей приведенной погрешности
δ=±γm·Gнорм/Gu
Из этих соотношений следует, что при измерениях, например вольтметром, в цепи при одном и том же значении напряжения относительная погрешность тем больше, чем меньше измеряемое напряжение. И если этот вольтметр выбран неправильно, то относительная погрешность может быть соизмерима со значением Gн, что является недопустимым. Заметим, что в соответствии с терминологией решаемых задач, например, при измерении напряжения G = U, при измерении тока C = I, буквенные обозначения в формулах для вычисления погрешностей необходимо заменять на соответствующие символы.
Пример 1.1. Вольтметром, имеющим значения γm= 1,0 %, Uн = Gнорм, Gk = 450 В, измеряют напряжение Uu, равное 10 В. Оценим погрешности измерений.
Решение.
Ответ. Погрешность измерений составляет 45 %. При такой погрешности измеренное напряжение нельзя считать достоверным.
При ограниченных возможностях выбора прибора (вольтметра), методическая погрешность может быть учтена поправкой, вычисленной по формуле
Пример 1.2. Вычислить абсолютную погрешность вольтметра В7-26 при измерениях напряжения в цепи постоянного тока. Класс точности вольтметра задан максимально приведенной погрешностью γm=±2,5 %. Используемый в работе предел шкалы вольтметра Uнорм=30 В.
Решение. Абсолютная погрешность вычисляется по известным формулам:
(так как приведенная погрешность, по определению, выражается формулой , то отсюда можно найти и абсолютную погрешность:
Ответ. ΔU = ±0,75 В.
Важными этапами в процессе измерений являются обработка результатов и правила округления. Теория приближенных вычислений позволяет, зная степень точности данных, оценить степень точности результатов еще до выполнения действий: отобрать данные с надлежащей степенью точности, достаточной для обеспечения требуемой точности результата, но не слишком большую, чтобы избавить вычислителя от бесполезных расчетов; рационализировать сам процесс вычисления, освободив его от тех выкладок, которые не окажут влияния на точные цифры результаты.
При обработке результатов применяют правила округления.
- Правило 1. Если первая из отбрасываемых цифр больше пяти, то последняя из сохраняемых цифр увеличивается на единицу.
- Правило 2. Если первая из отбрасываемых цифр меньше пяти, то увеличение не делается.
- Правило 3. Если отбрасываемая цифра равняется пяти, а за ней нет значащих цифр, то округление производится на ближайшее четное число, т.е. последняя сохраняемая цифра остается неизменной, если она четная, и увеличивается, если она не четная.
Если за цифрой пять есть значащие цифры, то округление производится по правилу 2.
Применяя правило 3 к округлению одного числа, мы не увеличиваем точность округления. Но при многочисленных округлениях избыточные числа будут встречаться примерно столь же часто, как недостаточно. Взаимная компенсация погрешности обеспечит наибольшую точность результата.
Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной погрешностью.
Величина предельной погрешности не является вполне определенной. Для каждого приближенного числа должна быть известна его предельная погрешность (абсолютная или относительная).
Когда она прямо не указана, то подразумевается, что предельная абсолютная погрешность составляет половину единицы последнего выписанного разряда. Так, если приведено приближенное число 4,78 без указания предельной погрешности, то подразумевается, что предельная абсолютная погрешность составляет 0,005. Вследствие этого соглашения всегда можно обойтись без указания предельной погрешности числа, округленного по правилам 1-3, т.е., если приближенное число обозначить буквой α, то
, где Δn – предельная абсолютная погрешность; а δn – предельная относительная погрешность.
Кроме того, при обработке результатов используются правила нахождения погрешности суммы, разности, произведения и частного.
- Правило 1. Предельная абсолютная погрешность суммы равна сумме предельных абсолютных погрешностей отдельных слагаемых, но при значительном числе погрешностей слагаемых обычно происходит взаимная компенсация погрешностей, поэтому истинная погрешность суммы лишь в исключительных случаях совпадает с предельной погрешностью или близка к ней.
- Правило 2. Предельная абсолютная погрешность разности равна сумме предельных абсолютных погрешностей уменьшаемого или вычитаемого.
Предельную относительную погрешность легко найти, вычислив предельную абсолютную погрешность.
- Правило 3. Предельная относительная погрешность суммы (но не разности) лежит между наименьшей и наибольшей из относительных погрешностей слагаемых.
Если все слагаемые имеют одну и ту же предельную относительную погрешность, то и сумма имеет ту же предельную относительную погрешность. Иными словами, в этом случае точность суммы (в процентном выражении) не уступает точности слагаемых.
В противоположность сумме разность приближенных чисел может быть менее точной, чем уменьшаемое и вычитаемое. Потеря точности особенно велика в том случае, когда уменьшаемое и вычитаемое мало отличаются друг от друга.
- Правило 4. Предельная относительная погрешность произведения приближенно равна сумме предельных относительных погрешностей сомножителей: δ=δ1+δ2, или, точнее, δ=δ1+δ2+δ1δ2 где δ – относительная погрешность произведения, δ1δ2 – относительные погрешности сомножителей.
Примечания:
1. Если перемножаются приближенные числа с одним и тем же количеством значащих цифр, то в произведении следует сохранить столько же значащих цифр. Последняя из сохраняемых цифр будет не вполне надежна.
2. Если некоторые сомножители имеют больше значащих цифр, чем другие, то до умножения следует первые округлить, сохранив в них столько цифр, сколько имеет наименее точный сомножитель или еще одну (в качестве запасной), дальнейшие цифры сохранять бесполезно.
3. Если требуется, чтобы произведение двух чисел имело заранее данное число вполне надежное, то в каждом из сомножителей число точных цифр (полученное измерением или вычислением) должно быть на единицу больше. Если количество сомножителей больше двух и меньше десяти, то в каждом из сомножителей число точных цифр для полной гарантии должно быть на две единицы больше, чем требуемое число точных цифр. Практически же вполне достаточно взять лишь одну лишнюю цифру.
- Правило 5. Предельная относительная погрешность частного приближенно равна сумме предельных относительных погрешностей делимого и делителя. Точная величина предельной относительной погрешности всегда превышает приближенную. Процент превышения примерно равен предельно относительной погрешности делителя.
Пример 1.3. Найти предельную абсолютную погрешность частного 2,81 : 0,571.
Решение. Предельная относительная погрешность делимого есть 0,005:2,81=0,2%; делителя – 0,005:0,571=0,1%; частного – 0,2% + 0,1%=0,3%. Предельная абсолютная погрешность частного приближенно составит 2,81:0,571·0,0030=0,015
Значит, в частном 2,81:0,571=4,92 уже третья значащая цифра не надежна.
Ответ. 0,015.
Пример 1.4. Вычислить относительную погрешность показаний вольтметра, включенного по схеме (рис. 1.3), которая получается, если предположить, что вольтметр имеет бесконечно большое сопротивление и не вносит искажений в измеряемую цепь. Классифицировать погрешность измерения для этой задачи.
рис. 1.3
Решение. Обозначим показания реального вольтметра через И, а вольтметра с бесконечно большим сопротивлением через И∞. Искомая относительная погрешность
Заметим, что
,
тогда получим
Так как RИ >>R и R > r, то дробь в знаменателе последнего равенства много меньше единицы. Поэтому можно воспользоваться приближенной формулой , справедливой при λ≤1 для любого α. Предположив, что в этой формуле α = -1 и λ= rR (r+R)-1 RИ-1, получим δ ≈ rR/(r+R) RИ.
Чем больше сопротивление вольтметра по сравнению с внешним сопротивлением цепи, тем меньше погрешность. Но условие R<<RИ – достаточное, но не необходимое условие малости δ. Погрешность будет мала также и в том случае, когда выполняется условие r≤RИ, т.е. сопротивление вольтметра много больше внутреннего сопротивления источника тока. При этом внешнее сопротивление может быть как угодно велико.
Ответ. Погрешность систематическая методическая.
Пример 1.5. В цепь постоянного тока (рис.1.4) включены приборы: А – амперметр типа М 330 класса точности КА = 1,5 с пределом измерения Ik = 20 А; А1 – амперметр типа М 366 класса точности КА1 = 1,0 с пределом измерения Iк1 = 7,5 А. Найти наибольшую возможную относительную погрешность измерения тока I2 и возможные пределы его действительного значения, если приборы показали, что I=8,0А. и I1 = 6,0А. Классифицировать измерение.
рис. 1.4
Решение. Определяем ток I2 по показаниям прибора (без учета их погрешностей): I2=I-I1=8,0-6,0=2,0 А.
Найдем модули абсолютных погрешностей амперметров А и А1
Для А имеем равенство для амперметра
Найдем сумму модулей абсолютных погрешностей:
Следовательно, наибольшая возможная и той же величины, выраженная в долях этой величины, равна 1 . 103 – для одного прибора; 2·103 – для другого прибора. Какой из этих приборов будет наиболее точным?
Решение. Точность прибора характеризуется значением, обратным погрешности (чем точнее прибор, тем меньше погрешность), т.е. для первого прибора это составит 1/(1 . 103) = 1000, для второго – 1/(2 . 103) = 500. Заметим, что 1000 > 500. Следовательно, первый прибор точнее второго в два раза.
К аналогичному выводу можно прийти, проверив соответствие погрешностей: 2 . 103 / 1 . 103 = 2.
Ответ. Первый прибор в два раза точнее второго.
Пример 1.6. Найти сумму приближенных замеров прибора. Найти количество верных знаков: 0,0909 + 0,0833 + 0,0769 + 0.0714 + 0,0667 + 0.0625 + 0,0588+ 0,0556 + 0,0526.
Решение. Сложив все результаты замеров, получим 0,6187. Предельная наибольшая погрешность суммы 0,00005·9=0,00045. Значит, в последнем четвертом знаке суммы возможна ошибка до 5 единиц. Поэтому округляем сумму до третьего знака, т.е. тысячных, получаем 0,619 – результат, в котором все знаки верные.
Ответ. 0,619. Количество верных знаков – три знака после запятой.
| 1. Метрология< Предыдущая | Следующая >1.2. Вероятный подход к оценке измерений |
|---|
xn—-8sbnaarbiedfksmiphlmncm1d9b0i.xn--p1ai
Расчет допусков и посадок подшипникового соединения. Пример решения задачи.
Требуется определить:
1. Систему данного соединения.2. Верхние и нижние отклонения посадочного внутреннего диаметра подшипника и диаметра вала.
3. Предельные размеры посадочных диаметров подшипника и вала.
4. Допуски на изготовление внутреннего диаметра подшипника и вала (сначала подсчитать через их предельные размеры, а затем проверить через отклонения).
5. Предельные натяги или зазоры данного соединения.
6. Допуск посадки (сначала подсчитать через натяги или зазоры, а затем проверить через допуски на изготовление подшипника и шейки вала).
7. Выполнить графическое изображение полей допуска данного соединения в масштабе 1:1000, на котором показать их отклонения, предельные размеры и величины натяга или зазора.
Решение:
1. Данное соединение выполнено в системе отверстия, при этом отверстием является внутреннее кольцо подшипника, а валом – шейка чашки дифференциала заднего моста.
2. В соответствии с ГОСТ 3325-85 для подшипников класса точности 0 в основных типах соединений в системе отверстия применяется посадка L0/m6. При этом предельные отклонения отверстия и вала номинальным диаметром свыше 50 мм до 80 мм составляют:
Отверстие, |
Вал, |
||
Верхнее отклонение, |
Нижнее отклонение, |
Верхнее отклонение, |
Нижнее отклонение, |
0 |
-15 |
+45 |
+11 |
3. Исходя из величины предельных отклонений для отверстия и вала, определяем предельные размеры посадочных диаметров:
- Dmax = Dn = 75 мм;
- Dmin = Dn + EI = 75 + (- 0,015) = 74,985 мм;
- dmax = dn + es = 75 + 0,045 = 75,045 мм;
- dmin = dn – ei = 75 + 0,011 = 75,011 мм.
4. Определяем допуски через предельные размеры:
– на изготовление внутреннего диаметра подшипника:
TD = Dmax – Dmin = 75,0 – 74,985 = 0,015 мм = 15 мкм;
– на изготовление вала:
Td = dmax – dmin = 75,045 – 75,011 = 0,034 мм = 34 мкм.
Проверяем допуски на изготовление внутреннего диаметра подшипника и вала через предельные отклонения:
- TD =ES – EI = 0 – (-0,015) = 0,015 мм = 15 мкм;
- Td =es – ei = 0,045 – 0,011 = 0,034 мм = 34 мкм.
Результат проверочного расчета совпадает с предыдущим результатом, значит, расчет выполнен правильно.
5. Определяем предельные натяги или зазоры соединения.
Smax = Dmax – dmin = 75 – 75,011 = – 0,011 мм = -11 мкм.
Поскольку значение максимального зазора получилось отрицательным, следовательно, в посадке присутствует гарантированный натяг:
- Nmin = dmin – Dmax = 75,011- 75,0 = 0,011 мм = 11мкм;
- Nmax = dmax – Dmin = 75,045 – 74,985 = 0,060 мм = 60 мкм.
6. Определяем допуск посадки, который для данного соединения равен допуску натяга или разности максимального или минимального натягов:
ТП = Nmax – Nmin = 60 – 11 = 49 мкм = 0,049 мм.
Проверяем расчет через допуски на изготовление подшипника и шейки вала:
ТП = ТD + Тd = 15 + 34 = 49 мкм = 0,049 мм.
Результат проверочного расчета совпадает с предыдущим результатом, значит, расчет выполнен правильно.
7. По результатам расчетов выполняем графическое изображение полей допуска данного соединения в масштабе 1:1000, на котором показываем их отклонения, предельные размеры и величины натяга или зазора (см. рисунок 1).
Расположение полей допусков отверстия и вала указывает, что посадка выполнена с гарантированным натягом.
***
Пример решения задачи на расчет допусков и посадок резьбового соединения
k-a-t.ru
Информатики и радиоэлектроники
Министерство образования Республики Беларусь
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра метрологии и стандартизации
Метрология и измерения Учебно – методическое пособие
для индивидуальной работы студентов
всех специальностей
Под общей редакцией С.В. Лялькова
Минск 1999
УДК 621.317(075)
ББК 30:10
М 54
Авторы: А.П. Белошицкий, М.Ю. Дерябина, А.М. Кострикин, С.В. Ляльков, В.Т. Ревин
Метрология и измерения: Учебно-методическое пособие для индивидуальной работы студентов/ А.П. Белошицкий и др.; под общ. ред. С.В. Лялькова. – Мн.: БГУИР, 1999. -72 с.: ил. 1. ISBN 985-444-103-2
Учебно-методическое пособие «Метрология и измерения» предназначено для индивидуальной работы студентов, изучающих курсы измерений. Оно содержит краткие методические указания, список рекомендуемой литературы и НТД, контрольные вопросы, решения типовых задач и задачи для самостоятельного решения.
Пособие может быть использовано при проведении практических и лабораторных занятий, связанных с оценкой погрешностей получаемых результатов. Оно также будет полезно самому широкому кругу студентов, аспирантов и научно-педагогических работников при решении ими конкретных практических задач метрологии и стандартизации.
УДК 621.317(075)
ББК 30:10
ISBN 985-444-103-2 © Коллектив авторов, 1999
Содержание
1 | Погрешности средств измерений …………………………… | 4 |
2 | Обработка результатов измерений с однократными наблюдениями …………………………………………………… | 10 |
3 | Обработка результатов многократных наблюдений при прямых измерениях ………………………………………………… | 17 |
4 | Обработка результатов многократных наблюдений при косвенных измерениях ………………………………… | 30 |
5 | Обработка результатов наблюдений при совокупных и совместных измерениях………………………………….…. | 35 |
6 | Измерение напряжениЙ………………………………………………….…. | 40 |
7 | Измерение частоты, периода, интервалов времени и фазовых сдвигов………………………………………………….………. | 44 |
8 | Измерение параметров пассивных линейных двухполюсников …..……………………………………………. | 49 |
Литература …………………………………………………………………………..…… | 57 | |
1 ПОгрешности средств измерений
Рекомендуемая литература: [1, c.230-248], [3, с.15-19] [4, c.49-55], [5, c.51-61], [6, c.11-20, 32-36], [7, c.13-15], [11], [12]
Методические указания
При изучении темы необходимо особо обратить внимание на следующее:
– формы представления погрешностей средств измерений;
– правила выбора нормирующего значения ХN;
– способы нормирования и формы выражения пределов допускаемых погрешностей;
– обозначение классов точности средств измерений.
Контрольные вопросы
1 Что такое погрешность средства измерений?
2 Что такое основная и дополнительная погрешности средств измерений?
3 Какие существуют формы представления погрешностей средств измерений?
4 Какие существуют правила выбора нормирующего значения ХN?
5 Как регламентируются способы нормирования и формы выражения пределов допускаемых погрешностей?
6 Что такое класс точности средства измерения и чем он определяется?
7 Как обозначаются классы точности?
Решение типовых задач
Задача № 1
Определить пределы инструментальных абсолютной и относительной погрешностей измерения тока I = 67 мA, если измерения проводились магни-тоэлектрическим миллиамперметром с нулем в начале шкалы, классом точности 1.0 и пределом измерения А = 100 мA.
Решение
Для магнитоэлектрического миллиамперметра класс точности определяется
значением максимальной приведенной погрешности, т.е. = ±1,0 %.
Так как
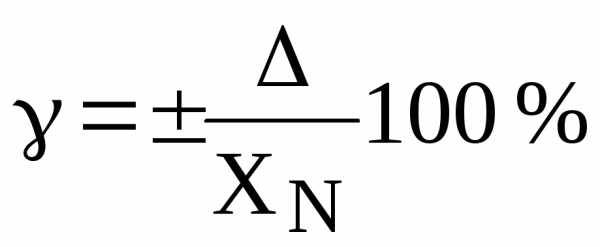 ,
,
то предел инструментальной абсолютной погрешности
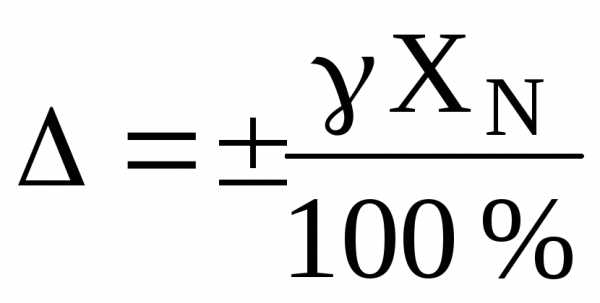 (мА).
(мА).
Миллиамперметр имеет равномерную шкалу с нулем в начале шкалы, и поэтому XN = A = 100 мA:
.
Предел инструментальной относительной погрешности
.
Задача № 2
Определить пределы инструментальных абсолютной и относительной погрешностей измерения напряжения U=8,6 B, если измерения проводились магнитоэлектрическим вольтметром с нулем в середине шкалы, классом точности 2,5 и пределами измерения А = ± 25 В.
Решение
Как и в предыдущей задаче, предел абсолютной погрешности находится из формулы:
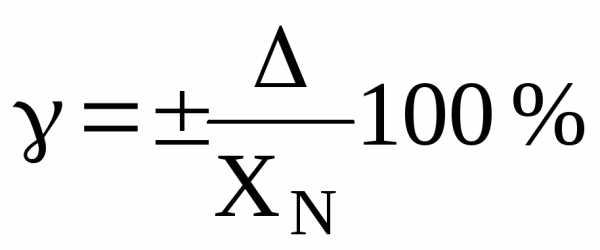 .
.
Вольтметр имеет равномерную шкалу с нулем в середине шкалы. Поэтому
XN = |25| + |25| = 50 (B),
= ±(2,550)/100 %=±1,25 (В).
Найдем предел относительной погрешности измерения:
= ±(/U)100 %= ±(1,25100)/8,6 ±15 (%).
Задача № 3
Oценить инструментальные погрешности измерения тока двумя магни-тоэлектрическими миллиамперметрами с классами точности 0,5 и 1.0 и указать, какой из результатов получен с большей точностью, а также, могут ли показания I1 = 19,0 мA и I2 = 18,6 мA исправных приборов отличаться так, как задано в условии? Миллиамперметры имеют нули в начале шкалы и пределы A1 =
= 50 мA и A2 = 20 мA.
Решение
Инструментальные абсолютные погрешности можно найти из формул:
1 = ±(1 ХN1)/100 %= ±(1 A1)/100 %= ±(0,550)/100 = ±0,25 (мA),
2 = ±(2 ХN2)/100 %= ±(2 A2)/100 %= ±(1,020)/100 = ±0,20 (мA).
Для определения, какое из измерений проведено с большей точностью, необходимо определить инструментальные относительные погрешности:
1 = ±(1/I1) 100 % = ±(0,25/19,0)100 % ±1,3 %,
2 = ±(2/I2) 100 % = ±(0,20/18,6)100 % ±1,1 %.
Видно, что второе измерение проведено с большей точностью, так как точность обратно пропорциональна модулю относительной погрешности.
В наихудшем случае (когда погрешности приборов будут иметь противоположные знаки) модуль разницы между результатами измерений || = |I1 – I2| не должен превышать сумму модулей абсолютных погрешностей, т.е.
|| < |1| + |2| .
Получаем
|| = 0,4 (мA) < |1| + |2| = 0,45 (мA).
Таким образом, при исправных миллиамперметрах можно получить указанные значения I1 и I2.
studfiles.net
Задачи по метрологии Задача 11
Выбор измерительных средств для контроля размеров
Условие. Выбрать универсальные измерительные средства для размеров отверстия и вала, указанных в задаче 1 (табл. 1.1) или полученных в задачах 2 или 3 (в зависимости от задания по гладким цилиндрическим соединениям).
Указания к решению
Для выбора средств и методов измерений линейных размеров от 1 до 500 мм при приемке изделий ГОСТ 8.051-81 устанавливает допускаемые погрешности измерений () в зависимости от допуска на изготовление изделия IT по квалитету и номинальному измеряемому размеру (табл. 11.1). Погрешности измерения являются наибольшими погрешностями измерений, включающими в себя все составляющие, зависящие от измерительных средств, установочных мер, температурных деформаций, базирования и т.д.
При допусках на изготовление, не соответствующих значениям, указанным в табл. 11.1, допускаемая погрешность выбирается по ближайшему меньшему значению допуска для соответствующего размера.
Существует связь между относительной погрешностью измерения
Амет() = мет/ IT (где мет – среднее квадратичное отклонение погрешности измерения), количеством m принятия бракованных деталей в качестве годных, количеством n неправильно забракованных деталей и вероятным предельным значением С выхода размера за каждую границу поля допуска у неправильно принятых деталей.
Предельные значения m, n и С приведены в табл. 11.2.
При определении параметров m, n и С рекомендуется принимать для квалитетов 2-7 Амет () = 0,16; для квалитетов 8-9 Амет () = 0,12; для квалитетов 10 и грубее Амет () = 0,1.
В случае отсутствия измерительного средства с требуемой погрешностью измерения СИ назначают приемочные границы путем смещения их внутрь допуска на деталь на величину С.
Предельное значение С можно рассчитать по формуле С = Сдоп – Спр,
где Сдоп – допустимое значение С, определяемое по табл. 11.2 в зависимости от допуска на изготовление IT;
Спр – принятое значение С, определяемое по тому допуску IT, который по табл. 11.1 соответствует погрешности измерения СИ выбранного измерительного средства.
Результаты выбора измерительного средства заносятся в табл. 11.3.
Справочные данные для выбора измерительных средств приведены в табл. 11.4.
Таблица 11.1
Допускаемые погрешности измерений для линейных размеров (гост 8.051-81, ст сэв 303-76)
Номинальные размеры, мм | К в а л и т е т ы | |||||||||||||
2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||||||
м к м | ||||||||||||||
1Т | | 1Т | | 1Т | | 1Т | | 1Т | | 1Т | | 1Т | | |
До 3 | 1,2 | 0,4 | 2,0 | 0,8 | 3 | 1,0 | 4 | 1,4 | 6 | 1,8 | 10 | 3,0 | 11 | 3,0 |
Св. 3 до 6 | 1,5 | 0,6 | 2,5 | 1,0 | 4 | 1,4 | 5 | 1,6 | 8 | 2,0 | 12 | 3,0 | 18 | 4,0 |
Св.6 до 10 | 1,5 | 0,6 | 2,5 | 1,0 | 4 | 1,4 | 6 | 2,0 | 9 | 2,0 | 15 | 4,0 | 22 | 5,0 |
Св.10 до 18 | 2,0 | 0,8 | 3,0 | 1,2 | 5 | 1,6 | 8 | 2,8 | 11 | 3,0 | 18 | 5,0 | 27 | 7,0 |
Св.18 до 30 | 2,5 | 1,0 | 4,0 | 1,4 | 6 | 2,0 | 9 | 3,0 | 13 | 4,0 | 21 | 6,0 | 38 | 8,0 |
Св.30 до 50 | 2,5 | 1,0 | 4,0 | 1,4 | 7 | 2,4 | 11 | 4,0 | 16 | 5,0 | 25 | 7,0 | 39 | 10,0 |
Св.50 до 80 | 3,0 | 1,2 | 5,0 | 1,8 | 8 | 2,8 | 13 | 4,0 | 19 | 5,0 | 30 | 9,0 | 46 | 12,0 |
Св.80 до 120 | 4,0 | 1,6 | 6,0 | 2,0 | 10 | 3,0 | 15 | 5,0 | 22 | 6,0 | 35 | 10,0 | 54 | 12,0 |
Св.120 до 180 | 5,0 | 2,0 | 8,0 | 2,8 | 12 | 4,0 | 18 | 6,0 | 25 | 7,0 | 40 | 12,0 | 63 | 16,0 |
Св.180 до 250 | 7,0 | 2,8 | 10,0 | 4,0 | 14 | 5,0 | 20 | 7,0 | 29 | 8,0 | 46 | 12,0 | 72 | 18,0 |
Св.250 до 315 | 8,0 | 3,0 | 12,0 | 4,0 | 16 | 5,0 | 23 | 8,0 | 32 | 10,0 | 52 | 14,0 | 81 | 20,0 |
Св.315 до 400 | 9,0 | 3,0 | 13,0 | 5,0 | 18 | 6,0 | 25 | 9,0 | 36 | 10,0 | 57 | 16,0 | 89 | 24,0 |
Св.400 до 500 | 10,0 | 4,0 | 15,0 | 5,0 | 20 | 6,0 | 27 | 9,0 | 40 | 12,0 | 63 | 18,0 | 97 | 26,0 |
Окончание табл. 11.1
Номинальные размеры, мм | К в а л и т е т ы | |||||||||||||||||
9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | ||||||||||
м к м | ||||||||||||||||||
1Т | | 1Т | | 1Т | | 1Т | | 1Т | | 1Т | | 1Т | | 1Т | | 1Т | | |
До 3 | 25 | 6 | 40 | 8 | 60 | 12 | 100 | 20 | 140 | 30 | 250 | 50 | 400 | 80 | 600 | 120 | 1000 | 200 |
Св. 3 до 6 | 30 | 8 | 48 | 10 | 75 | 16 | 120 | 30 | 180 | 40 | 300 | 60 | 480 | 100 | 750 | 160 | 1200 | 240 |
Св.6 до 10 | 36 | 9 | 58 | 12 | 90 | 18 | 150 | 30 | 220 | 50 | 360 | 80 | 580 | 120 | 900 | 200 | 1500 | 300 |
Св.10 до 18 | 43 | 10 | 70 | 14 | 110 | 30 | 180 | 40 | 270 | 60 | 430 | 90 | 700 | 140 | 1100 | 240 | 1800 | 380 |
Св.18 до 30 | 52 | 12 | 84 | 18 | 130 | 30 | 210 | 50 | 330 | 70 | 520 | 120 | 840 | 180 | 1300 | 280 | 2100 | 440 |
Св.30 до 50 | 62 | 16 | 100 | 20 | 160 | 40 | 250 | 50 | 390 | 80 | 620 | 140 | 1000 | 200 | 1600 | 320 | 2500 | 500 |
Св.50 до 80 | 74 | 18 | 120 | 30 | 190 | 40 | 300 | 60 | 460 | 100 | 740 | 160 | 1200 | 240 | 1900 | 400 | 3000 | 600 |
Св.80 до 120 | 87 | 20 | 140 | 30 | 220 | 50 | 350 | 70 | 540 | 120 | 870 | 180 | 1400 | 280 | 2200 | 440 | 3500 | 700 |
Св.120 до 180 | 100 | 30 | 160 | 40 | 250 | 50 | 400 | 80 | 630 | 140 | 1000 | 200 | 1600 | 320 | 2500 | 500 | 4000 | 800 |
Св.180 до 250 | 115 | 30 | 185 | 40 | 290 | 60 | 400 | 100 | 720 | 160 | 1150 | 240 | 1850 | 380 | 2900 | 600 | 4600 | 1000 |
Св.250 до 315 | 130 | 30 | 210 | 50 | 320 | 70 | 520 | 120 | 810 | 180 | 1300 | 260 | 2100 | 440 | 3200 | 700 | 5200 | 1100 |
Св.315 до 400 | 140 | 40 | 230 | 50 | 360 | 80 | 570 | 120 | 890 | 180 | 1400 | 280 | 2300 | 460 | 3600 | 800 | 5700 | 1200 |
Св.400 до 500 | 155 | 40 | 250 | 50 | 400 | 80 | 630 | 140 | 970 | 200 | 1550 | 320 | 2500 | 500 | 4000 | 800 | 6300 | 1400 |
Примечание. Разрешается увеличение допускаемой погрешности измерения при уменьшении размера, учитывающего это увеличение, а также в случае разделения на размерные группы для селективной сборки.
Таблица 11.2
Амет () | m | n | C/IT | Амет () | m | n | C/IT |
% | % | ||||||
1,6 3,0 5,0 8,0 | 0,37 – 0,39 0,87 – 0,90 1,60 – 1,70 2,60 – 2,80 | 0,70 – 0,75 1,20 – 1,30 2,00 – 2,25 3,40 – 3,70 | 0,01 0,03 0,06 0,10 | 10,0 12,0 16,0 | 3,10 – 3,50 3,75 – 4,11 5,00 – 5,40 | 4,50 – 4,75 5,40 – 5,80 7,80 – 8,25 | 0,14 0,17 0,25 |
Примечание. Первые значенияmиnсоответствуют закону нормального распределения погрешности измерения, вторые – закону равной вероятности. При неизвестном законе распределения погрешности измерения значенияmиnможно определять как среднее из приведенных значений.
Пример. Выбрать универсальные измерительные средства для измерения диаметра отверстия 100Н8, диаметра вала 100f7 и длины вала l = 80 мм по среднему классу точности.
studfiles.net
Решение типовых задач метрологии – n1.doc
Решение типовых задач метрологииДоступные файлы (1):
n1.doc
Задача №1Погрешности средств измерений
Номинальный режим электроустановки постоянного тока характеризуется напряжением U
и током I, измерение которых может быть произведено вольтметрами V или V и амперметрами А или А. Значения напряжения U, тока I и характеристики электроизмерительных приборов приведены в таблице 1.1.
Необходимо:
а) из двух вольтметров и двух амперметров выбрать электроизмерительные приборы, обеспечивающие меньшую возможную относительную погрешность;
б) определить пределы, в которых могут находиться действительные значения напряжения и тока при их измерении выбранными приборами;
в) определить возможную относительную погрешность в определении мощности установки по показаниям вольтметра и амперметра.
Таблица 1.1
Группа
Величина
Вариант
91
А
Напряжение U,В
27Вольтметры
V
Класс точностиПредел измерения U,В
4
30V
Класс точностиПредел измерения U,В
1,5
50Б
Ток I, А
2,5
Амперметры
А
Класс точностиПредел измерения I,А
4,0
3
А
Класс точностиПредел измерения I,А
1,0
15
а)Максимальные абсолютные погрешности амперметра и вольтметра:
[%] [%]
б)Найдём относительную погрешность в процентах
Из двух амперметров выбираем А1 так как .
Из двух вольтметров выбираем V2 так как .
2. Определим пределы в которых могут находится действительные значения напряжения и тока при их измерении выбранными приборами:
Для V2 В В
Для А1 А А
3. определим возможную относительную погрешность в определении мощности установки по показаниям вольтметра и амперметра.
Для A1 иV2:
Задача №2
Определение погрешности результата косвенных измерений
Для измерения сопротивления или мощности косвенным методом использовались два прибора: амперметр и вольтметр магнитоэлектрической системы.
Определить:
а) величину сопротивления и мощность по показаниям приборов;
б) максимальные абсолютные погрешности амперметра и вольтметра;
в) абсолютную погрешность косвенного метода;
г) относительную погрешность измерения;
д) пределы действительных значений измеряемых физических величин.
Наименование заданной величины
Значение величины
Предел измерения U,В
250
Класс точности ,%
0,5
Показания вольтметра U, В
240
Предел измерения I, А
1.5
Класс точности ,%
1.0
Показание амперметра I, А
1,2
Методические указания
При косвенных измерениях искомое значение величины y находится на основании математической зависимости, связывающей эту величину с несколькими величинами x, x, ……x, измеряемыми прямыми методами. При этом погрешности прямых измерений приводят к тому, что окончательный результат имеет погрешность.
Максимальные абсолютные погрешности амперметра и вольтметра определяются:
I = ,
U=
где – приведенная погрешность измерительного прибора, равная классу точности прибора;
I, U- номинальное значение тока и напряжения;
Формулы для расчета абсолютных и относительных погрешностей результата косвенных измерений:
где x , x – измеренные значения электрических величин; , – максимальные абсолютные погрешности, допускаемые при измерении значений x , x.Функция x * x
используется в задаче для расчета погрешности косвенного измерения мощности, функция x/ x – то же для сопротивлений.
Результаты вычислений сопротивлений и мощности сводятся в таблицу:
| U, В | I, A | U, B | I, A | P, Вт | R,Ом | | | Р+Р, Вт | R+R, Ом |
| 250 | 1,5 | 1,25 | 0,015 | 3.9 | 2,708 | 0,014 | 4 | 288 3,9 | 200±2.708 |
Расчет
значение мощности и сопротивления по показаниям приборов
Р = UI = = 288 Вт;
предельные абсолютные погрешности измерительных приборов:
амперметра – I = = = 0,015 А;
вольтметра U= = = 1,25 В;
абсолютная погрешность косвенного измерения мощности и сопротивления:
Р= Вт;
Ом
относительная погрешность косвенного измерения мощности и сопротивления:
= = 0,014;
;
действительное значение мощности Р = (288 3,9) Вт.
действительное значение сопротивления R=(200±2,708) Ом
Задача №3
Применение масштабных измерительных преобразователей для измерения тока и напряжения
Измерительный механизм (ИМ) магнитоэлектрической системы рассчитан на ток I и напряжение U и имеет шкалу на делений. Необходимо :
а) составить схему включения ИМ с шунтом и дать вывод формулы R;
б) определить постоянную ИМ по току С, величину сопротивления шунта Rи постоянную амперметра С, если этим прибором нужно измерять ток I;
в) определить мощность, потребляемую амперметром при номинальном значении тока I;
г) составить схему включения ИМ с добавочным сопротивлением и дать вывод формулы R;
д) определить постоянную ИМ по напряжению С, величину добавочного сопротивления R и постоянную вольтметра С, если этим прибором нужно намерять напряжение U;
е) определить мощность, потребляемую вольтметром при номинальном значении напряжения U.
Методические указания
Масштабный измерительный преобразователь предназначен для изменения значения измеряемой величины в заданное число раз.
Для расширения диапазона измерения измерительных приборов по напряжению и току применяют измерительные трансформаторы, добавочные сопротивления и шунты.
Измерительные трансформаторы переменного тока и напряжения применяют для расширения диапазона измерения электромагнитных, электродинамических, индукционных приборов по току и напряжению, а также для обеспечения безопасности измерений при высоком напряжении.
Шунты применяются для расширения диапазона измерения магнитоэлектрических измерительных приборов по току. Сопротивление индивидуального шунта рассчитывается по формуле:
R=
Где R- сопротивление измерительного прибора магнитоэлектрической системы;
N = I/ I- коэффициент шунтирования;
I,I-предел измерения прибора с шунтом и без него.
Добавочные резисторы служат для расширения пределов измерения по напряжению вольтметров различных систем и приборов, имеющих параллельные цепи, подключаемые к источнику напряжения.
Индивидуальный добавочный резистор рассчитывается по формуле :
R = R(m-1) , где m= U/ U- коэффициент преобразования напряжений;
U,U- пределы измерения прибора с добавочным резистором и без него.
а) Схема включения измерительного механизма с шунтом.
б) Ом
Ом
мА/ дел
А/ дел
в) Мощность потребляемая амперметром при номинальном значении тока Iн.
Вт
г) Схема включения измерительного механизма с добавочным сопротивлением.
д) Ом
Ом
мВ/дел
В/дел
е) Мощность потребляемая вольтметром при номинальном напряжении
Вт
Результаты сводятся в таблицу:
| R, Ом | С,мА/дел. | С,А/дел. | Р, Вт | R,Ом | С,мВ/дел | С,В/дел | Р,Вт |
| 0,133 | 0,067 | 0,006667 | 0,0325 | 44990 | 0,867 | 6 | 4,5 |
perviydoc.ru
Сборник задач по расчету погрешностей электрических измерений
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
___________________________
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
___________________________
МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ
(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
_______________________________________________________________________
В.А. Новиков, В.Ю.Кончаловский
Учебное пособие
по курсу
«Информационно-измерительная техника и электроника»
для студентов, обучающихся по направлению «Электроэнергетика»
Москва Издательство МЭИ 2006
УДК
621.317
Н731
Утверждено учебным управлением МЭИ в качестве учебного пособия для студентов
Подготовлено на кафедре информационно-измерительной техники МЭИ(ТУ)
Рецензенты: профессор каф.ММ МЭИ(ТУ) А.Б. Фролов,
профессор каф.ВМСС МЭИ(ТУ) И.И. Ладыгин,
доцент РГСУ Л.Л. Коленский .
Новиков В.А
Н731 Сборник задач по расчету погрешностей электрических измерений: учеб. пособие / В.А. Новиков, В.Ю. Кончаловский — М. : Издательство МЭИ, 2006. — 36 с.
ISBN5-7046-1328-4
Рассматриваются задачи по расчету характеристик погрешностей прямых и косвенных измерений с однократными наблюдениями. Сборник включает четыре раздела и предполагает двухступенчатую подготовку обучаемого. На первой ступени рекомендуются задачи первого и второго разделов, на второй — третьего и четвертого. Первый и второй разделы содержат сравнительно простые задачи, каждая из которых связана с решением той или иной части общей задачи по оцениванию погрешностей измерений. Последующие два раздела состоят из более сложных задач, приближенных к практике электрических измерений.
Каждый раздел содержит примеры задач с решениями и задачи с ответами для самопроверки.
Для студентов, изучающих методику метрологических расчетов в рамках общего курса «Информационно-измерительная техника и электроника».
ISBN 5-7046-1328-4© Московский энергетический институт (ТУ), 2006
Предисловие
Результат измерения электрической (как и любой физической) величины должен содержать информацию о точности полученного значения. Для этого используются те или иные характеристики погрешности измерения.
Расчет характеристик погрешности измерения, иначе называемый оцениванием погрешности, выполняется на основе имеющихся сведений об объекте измерения и используемых средствах измерений.
В зависимости от характера проявления преобладающих составляющих погрешности измерения, систематического или случайного, используют измерения соответственно с однократными или многократными наблюдениями. Выбранная методика измерений определяет и способ оценивания погрешностей.
В данном сборнике рассматриваются задачи по расчету характеристик погрешностей измерений с однократными наблюдениями. В качестве таких характеристик, чаще всего, используются симметричные доверительные интервалы для заданных значений доверительной вероятности.
Предлагаемое учебное пособие предназначено для студентов, изучающих методику метрологических расчетов в рамках общего курса «Информационно-измерительная техника и электроника». Поэтому, в силу ограниченности учебного времени, в методике расчетов допущены некоторые упрощения. При определении границ доверительных интервалов погрешностей для доверительных вероятностей 0,9, 0,95 и 0,99 используются усредненные значения коэффициента KP, не зависящие от составляющих погрешности измерения [1]. Кроме того, упрощено правило округления вычисленной характеристики погрешности: независимо от найденного числового значения оно округляется до двух значащих цифр.
studfiles.net



