Задачи производные с решениями – Примеры использования производной для нахождения наилучшего решения в прикладных задачах
- Комментариев к записи Задачи производные с решениями – Примеры использования производной для нахождения наилучшего решения в прикладных задачах нет
- Советы абитуриенту
Образцы решения задач по теме «Производные»
Вторая производная не определена в точке x = 0 и обращается в ноль в точкеx = 4/3. Дальнейшее исследование оформим в виде таблицы, аналогичной табл. 1.
|
|
|
|
| Табл. 2 |
| (−∞;0) | 0 | (0; 4/3) | 4/3 | (4 / 3; +∞) |
′′ | + | не определ. | – | 0 | + |
f (x) | |||||
f (x) |
| не определ. | ∩ | т. перегиба |
|
В табл. 2 символ « » означает, что график функции представляет собой вогнутую (выпуклую вниз) кривую, а символ « ∩» – выпуклую (выпуклую вверх) кривую.
Таким образом, график является выпуклым вниз на промежутках (−∞;0) и(4 / 3; +∞) , и выпуклым вверх – на промежутке (0; 4/3). Точкаx = 4/3 представляет собой точку перегиба. Значение функции в точке перегиба
равно yпер. = f (4 / 3)= | (4 −2)27 | = | 27 . |
| 64 |
| 32 |
5. Поскольку в точке x = 0 функция имеет бесконечный разрыв, вертикальная прямаяx = 0, проходящая через эту точку, т. е. осьOy является вертикальной асимптотой графика функции.
Найдем наклонную асимптоту, заданную уравнением y =k x +b, в котором параметрыk иb определяются по формулам
|
|
|
|
| k = lim | f (x) | , | b = lim ( f(x) −kx). |
|
| ||
|
|
|
|
| x |
|
| |||||
|
|
|
|
|
| x→±∞ |
| x→±∞ |
|
|
| |
При | этом | если | x → +∞ получим | параметры k иb правой наклонной | ||||||||
асимптоты, а если x → −∞ – левой. В нашем случае |
|
|
| |||||||||
k = | lim |
| f (x) | = | lim | 3x −2 = 0 , | b = lim ( f(x) −kx)= | lim | 3x −2 | = 0 . | ||
|
| x3 | ||||||||||
| x→±∞ | x | x→±∞ | x4 |
|
| x→±∞ | x→±∞ |
| |||
Следовательно, горизонтальная прямая y = 0, т. е. осьOx является горизонтальной асимптотой графика данной функции (частный случай наклонной асимптоты).
6. Координаты точек пересечения графика функции с осью Ox найдем,
f (x)= 0 |
| 3x −2 | =0 | x = 2 / 3 |
| |||
| x3 | . | ||||||
решив систему | y = 0 | . В нашем случае получим |
|
| y = | 0 | ||
|
| y = 0 |
|
| ||||
|
|
|
|
|
|
| ||
График функции пересекает ось Ox в единственной точке (2/3; 0). Координаты точки пересечения графика функции с осьюOy находятся
| x = 0 | . Поскольку точка x = 0 не входит в область | |
из системы |
| f (0) | |
y = |
| ||
определения исследуемой функции, ее график не пересекает ось Oy.
7. График функции, построенный с помощью проведенного исследования, представлен на рис. 3.
studfiles.net
Производные(задачи)
II. ДИФФЕРЕНЦИРОВАНИЕ
Понятие производной. Производная функции
 .
.Геометрический смысл производной. Уравнения касательной и нормали к графику функции.
Понятие дифференцируемости функции и дифференциала. Условие дифференцируемости. Связь дифференциала с производной.
Геометрический смысл дифференциала.
Непрерывность дифференцируемой функции.
Дифференцирование постоянной и суммы, произведения и частного.
Производная сложной функции.
Инвариантность формы дифференциала.
Производная обратной функции.
Производные обратных тригонометрических функций.
Задача 5. Найти производную.
5.1.5.2.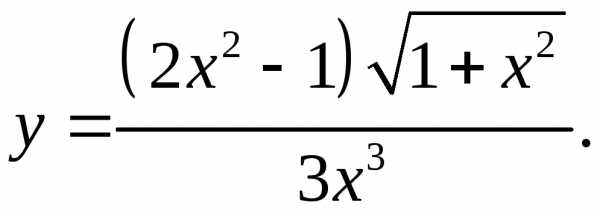
5.3. 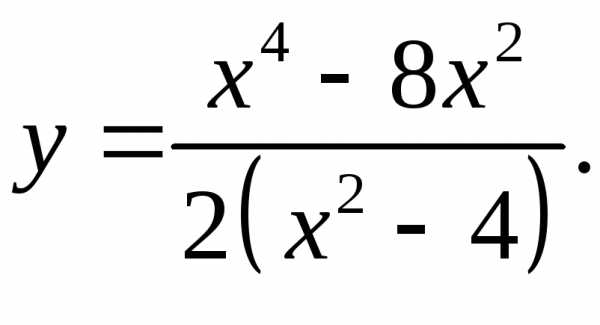 5.4.
5.4.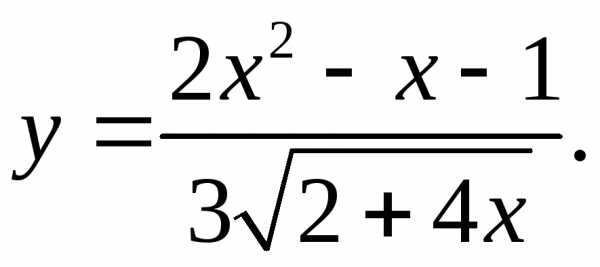
5.5. 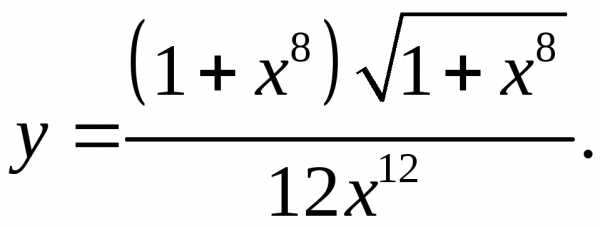 5.6.
5.6.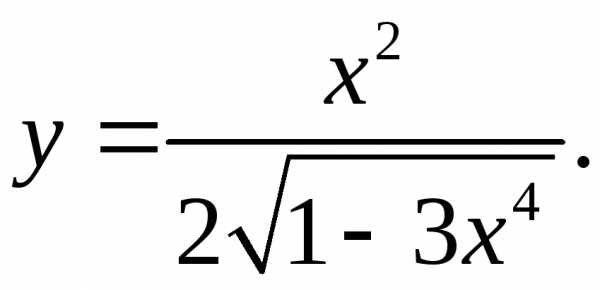
5.7. 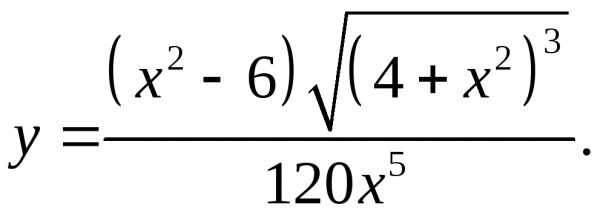 5.8.
5.8.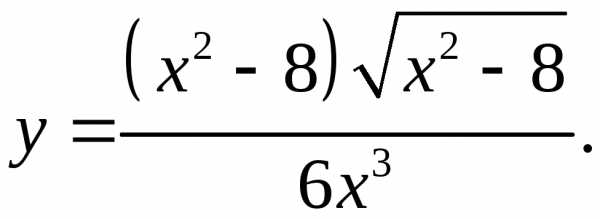
5.9. 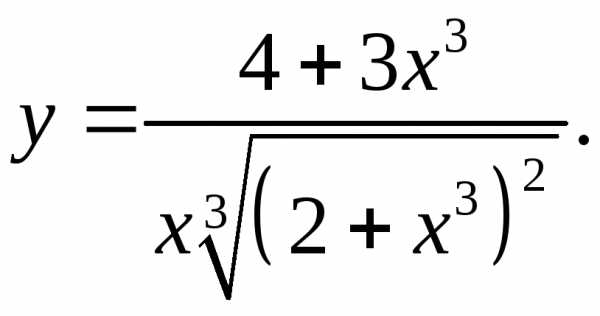 5.10.
5.10.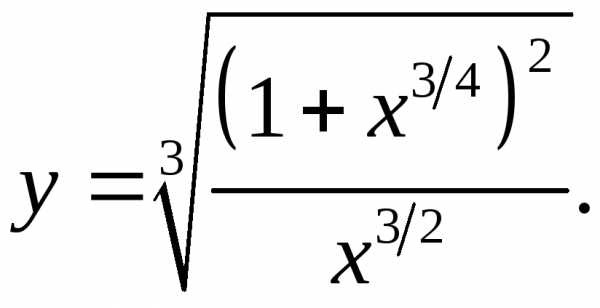
5.11. 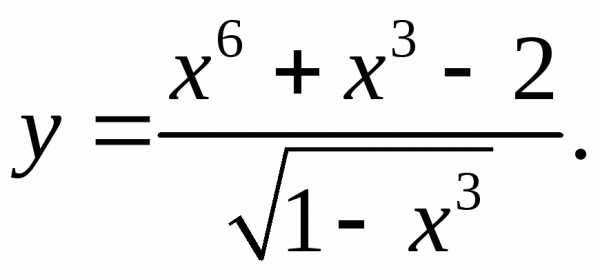 5.12.
5.12.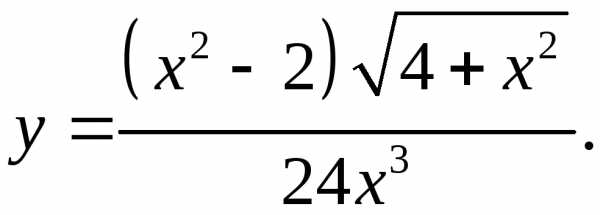
5.13. 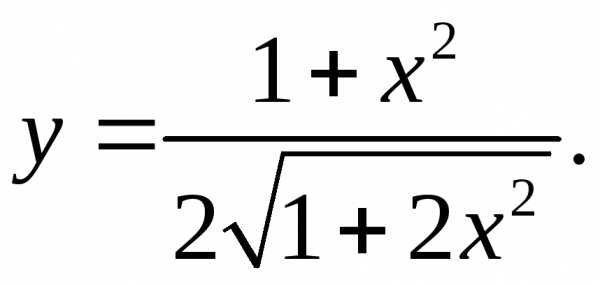 5.14.
5.14.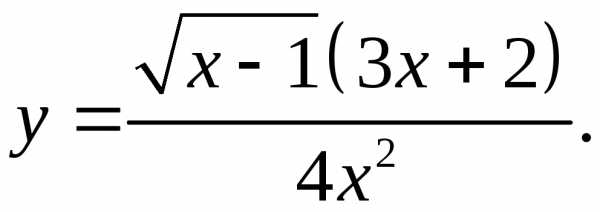
5.15. 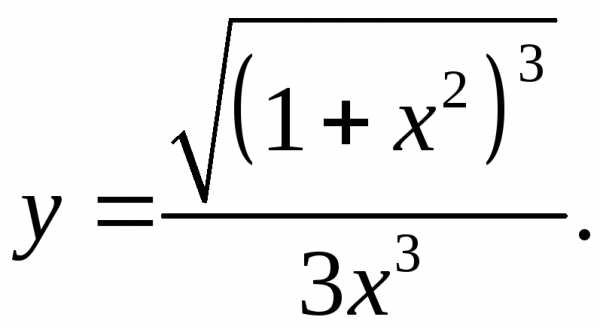 5.16.
5.16.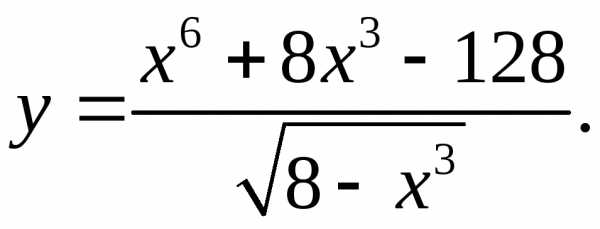
5.17. 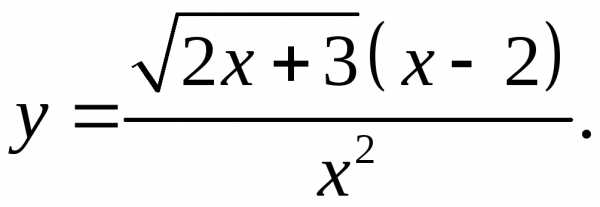 5.18.
5.18.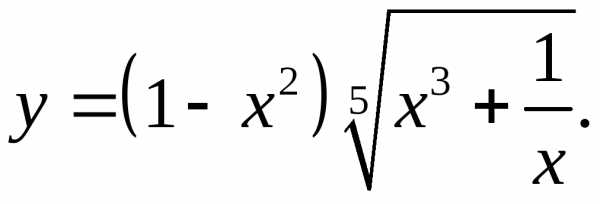
5.19. 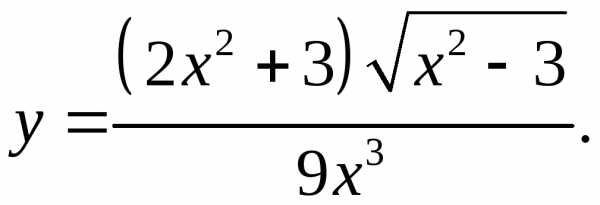
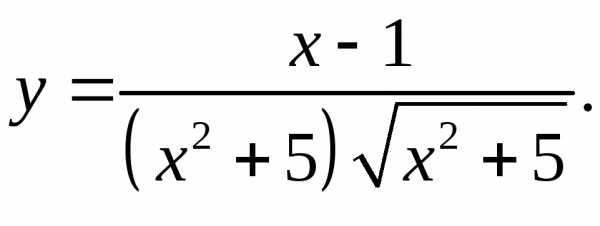
5.21. 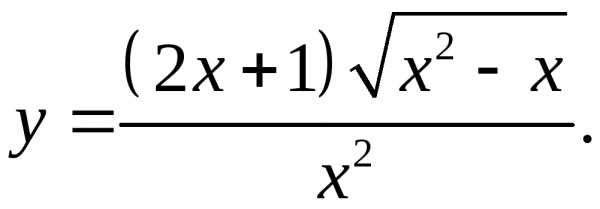 5.22.
5.22.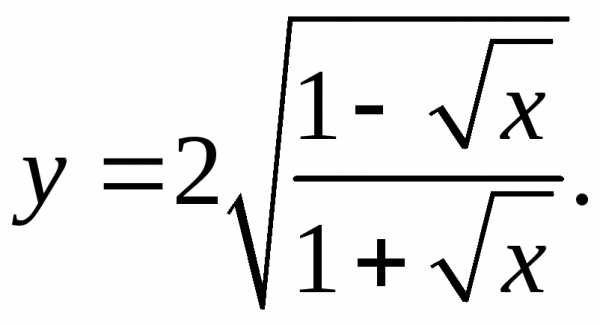
5.23.
5.24.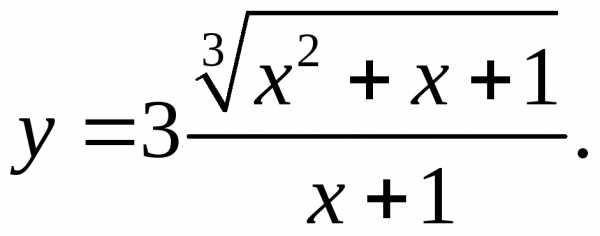
5.25. 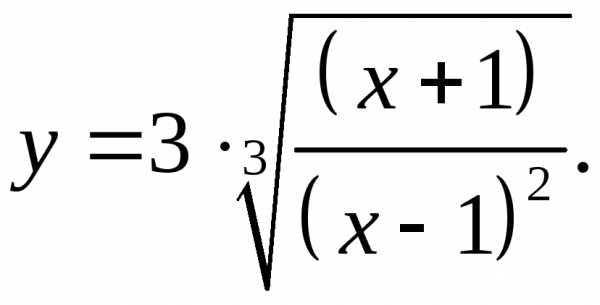 5.26.
5.26.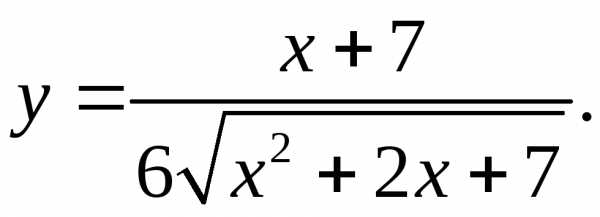
5.27. 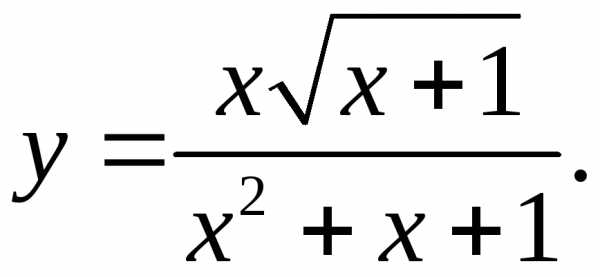 5.28.
5.28.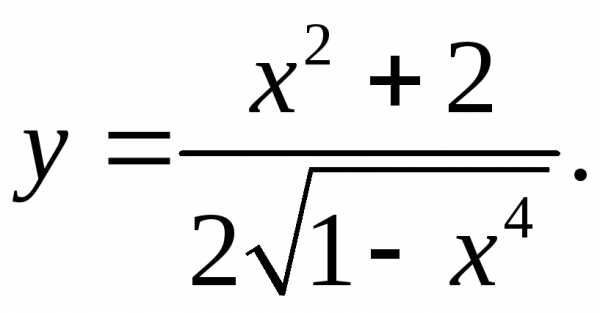
5.29.  5.30.
5.30.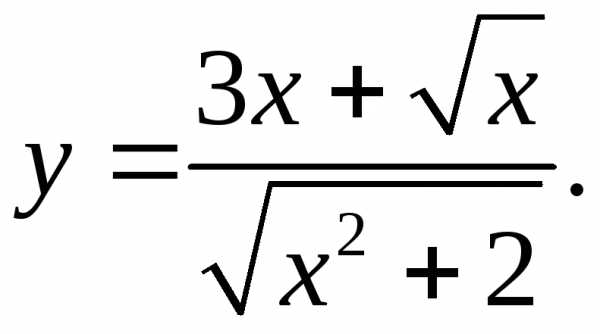
5.31.
Задача 6
6.1. 6.2.
6.3. 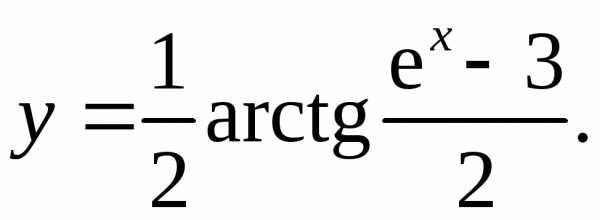 6.4.
6.4. 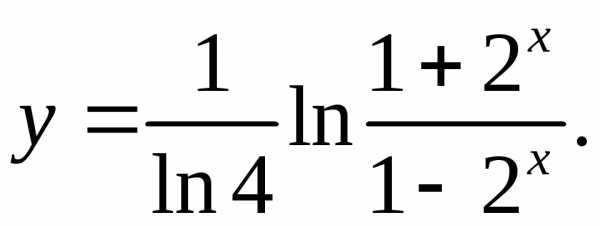
6.5. 6.6.
6.7. 6.8.
6.9. 6.10.
6.11. 6.12.
6.13.
6.14.
6.15.
6.16. 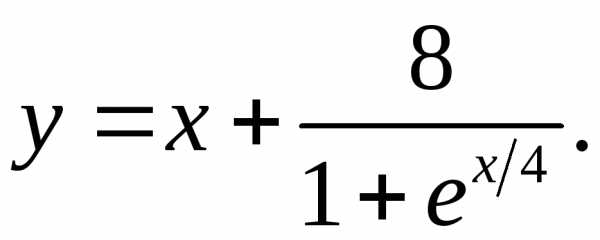
6.17.
6.18.
6.19.
6.20. 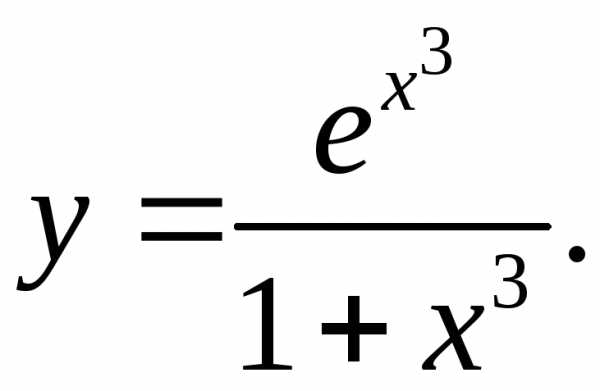
6.21. 6.22.
6.23. 6.24.
6.25.
6.26.
6.27.
6.28.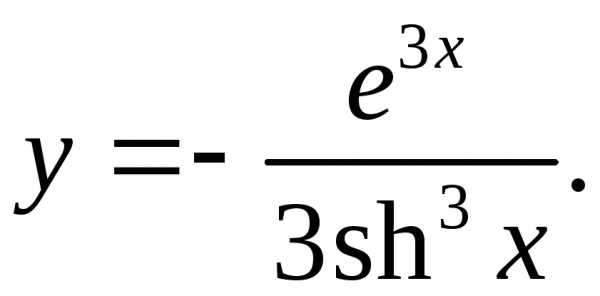
6.29. 6.30.
6.31. 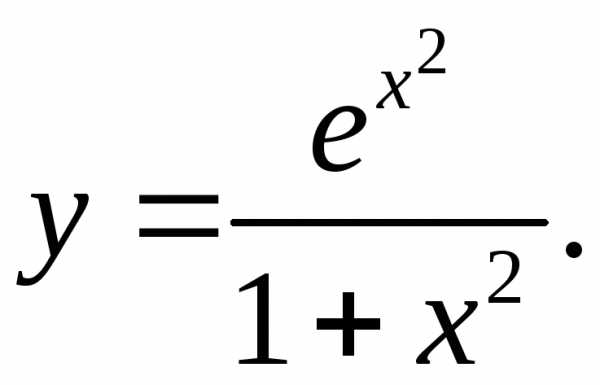
Задача 8. Найти производную.
8.1. 8.2.
8.3. 8.4.
8.5. 8.6.
8.7. 8.8.
8.9. 8.10.
8.11. 8.12.
8.13. 8.14.
8.15. 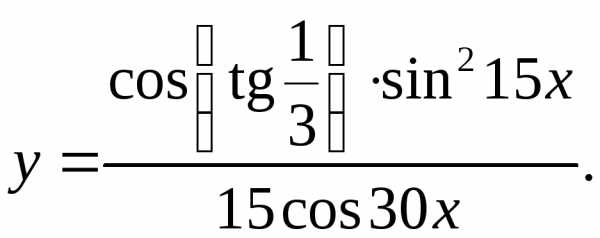 8.16.
8.16.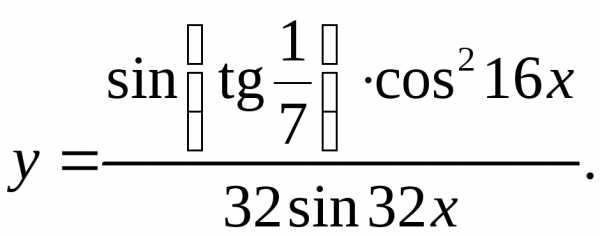
8.17. 8.18.
8.19. 8.20.
8.21. 8.22.
8.23. 8.24.
8.25. 8.26.
8.27. 8.28.
8.29. 8.30.
8.31.
9.1.
9.2.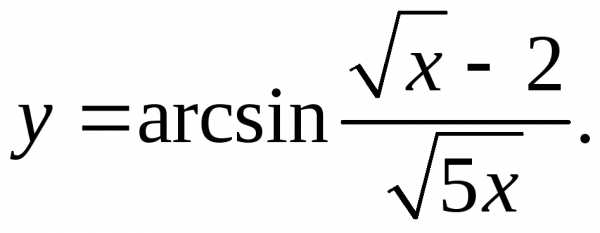
9.3.
9.4.
9.5. 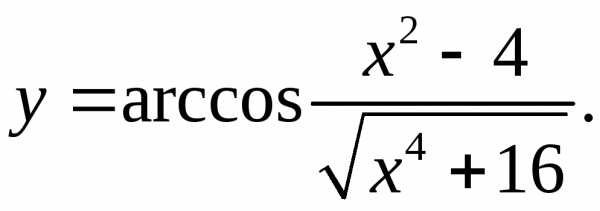 9.6.
9.6.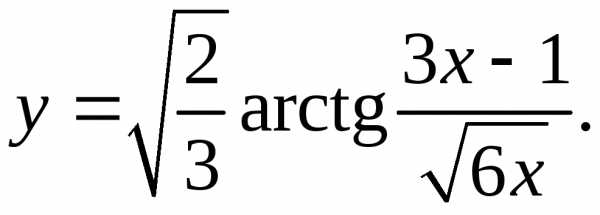
9.7.
9.8.
9.9. 9.10.
9.11. 9.12.
9.13. 9.14.
9.15. 9.16.
9.17.
9.18.
9.19.
9.20.
9.21.
9.22.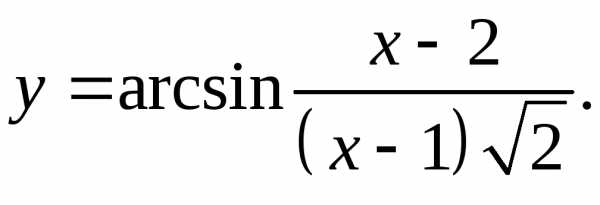
9.23. 9.24.
9.25. 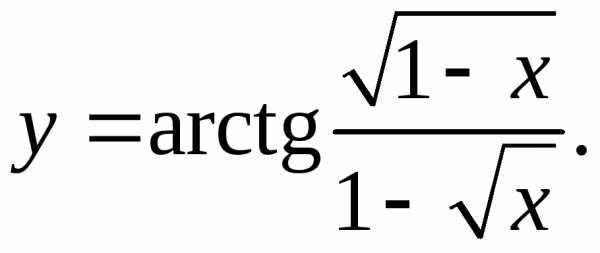 9.26.
9.26.
9.27.
9.28.
9.29.
9.30.
9.31.
Задача
17. Найти
производную 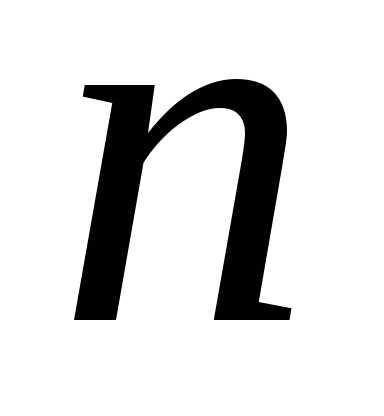 -го
порядка.
-го
порядка.
17.1. 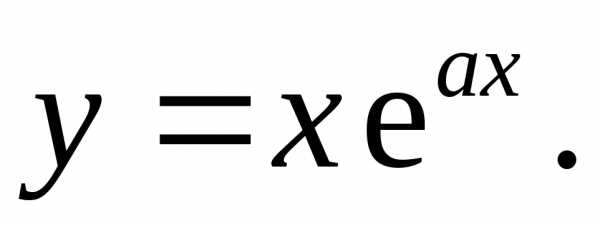 17.2.
17.2.
17.3. 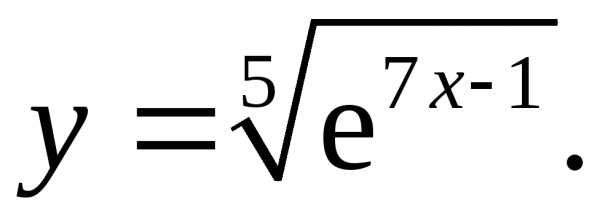 17.4.
17.4.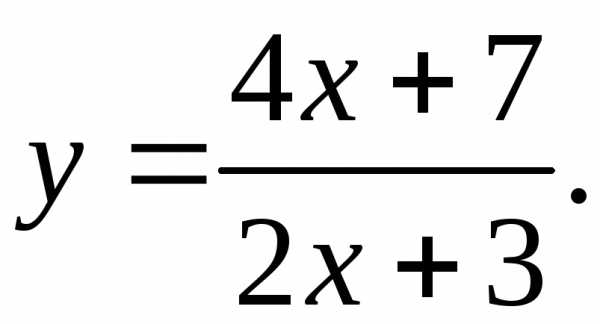
17.5.
17.6.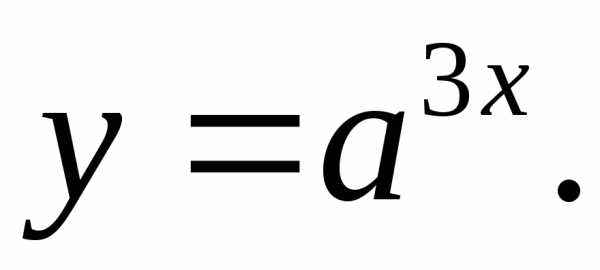
17.7. 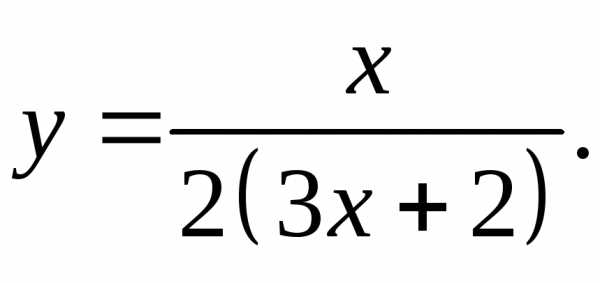 17.8.
17.8.
17.9. 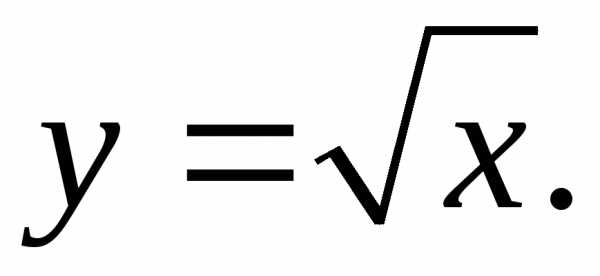 17.10.
17.10.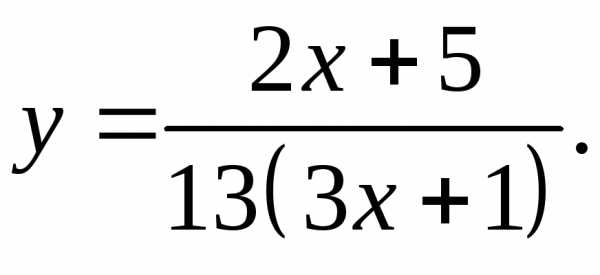
17.11. 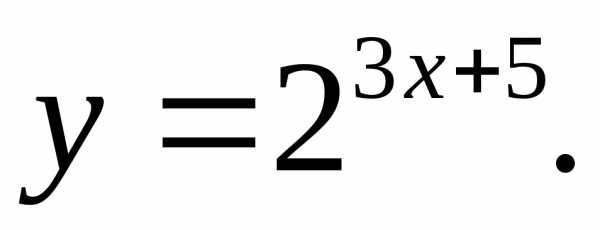 17.12.
17.12.
17.13. 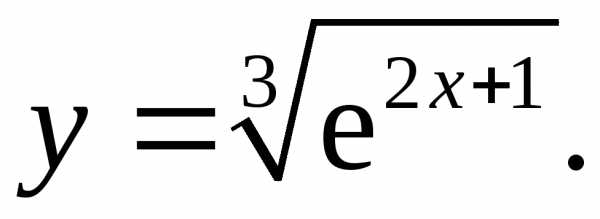 17.14.
17.14.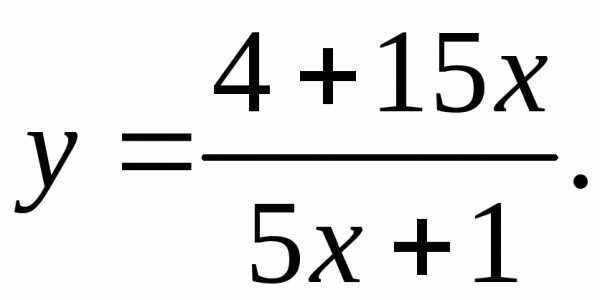
17.15.
17.16.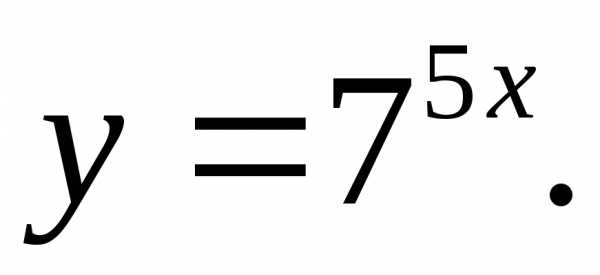
17.17. 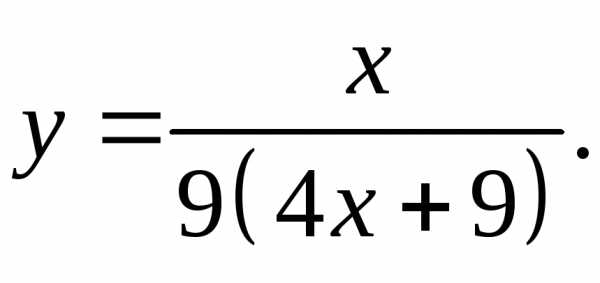 17.18.
17.18.
17.19. 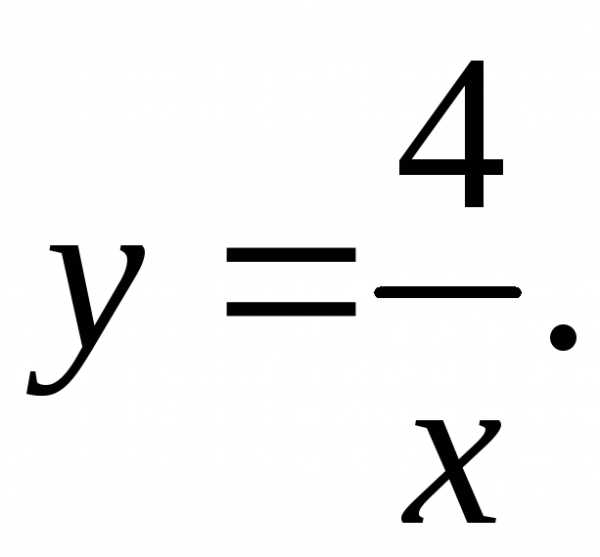 17.20.
17.20.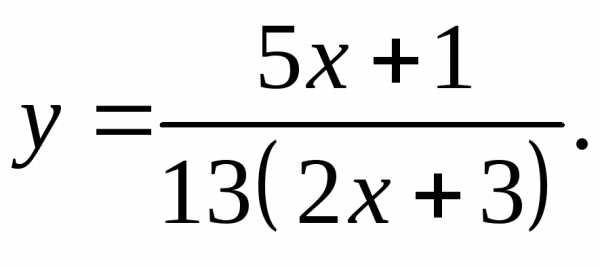
17.21. 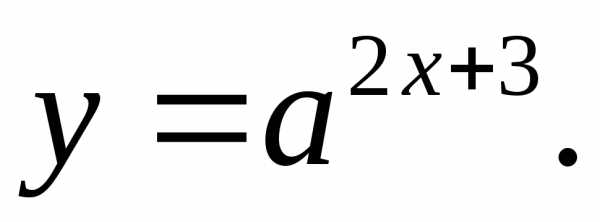 17.22.
17.22.
17.23. 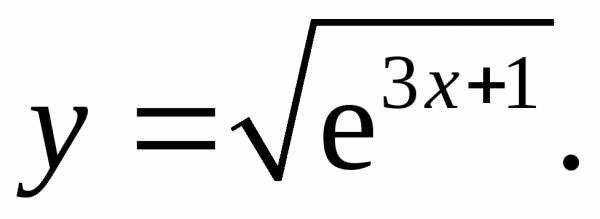 17.24.
17.24.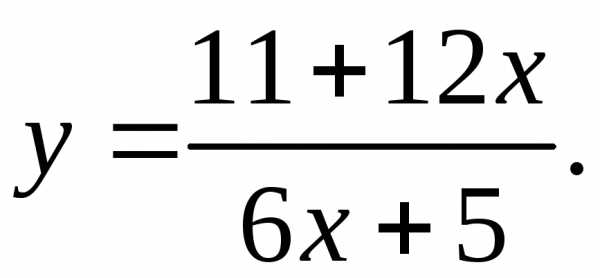
17.25.
17.26.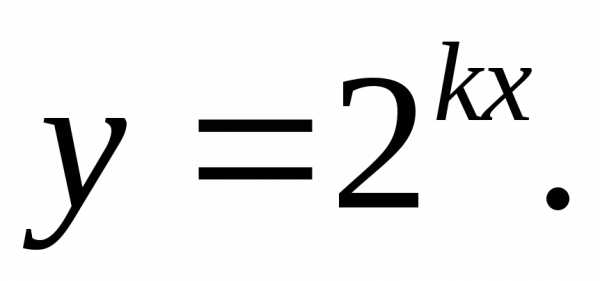
17.27. 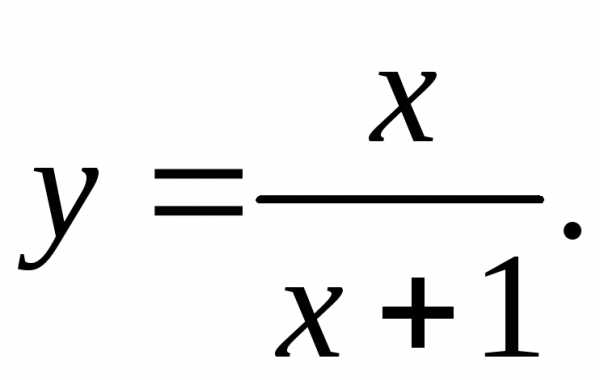 17.28.
17.28.
17.29. 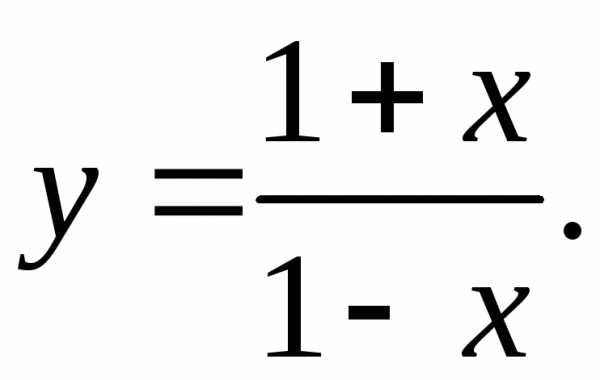 17.30.
17.30.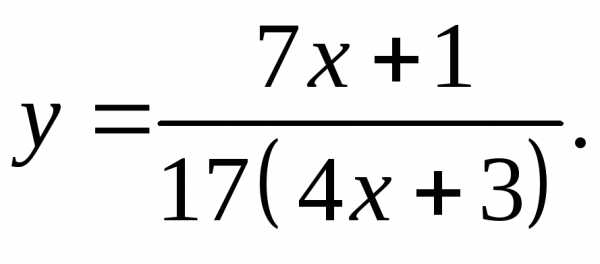
17.31. 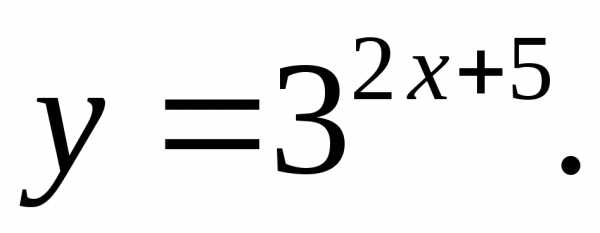
Задача 18. Найти производную указанного порядка.
18.1. 18.2.
18.3. 18.4.
18.5. 18.6.
18.7.
18.8.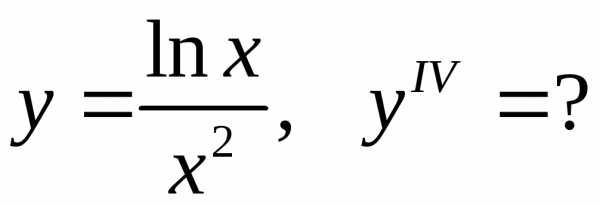
18.9. 18.10.
18.11. 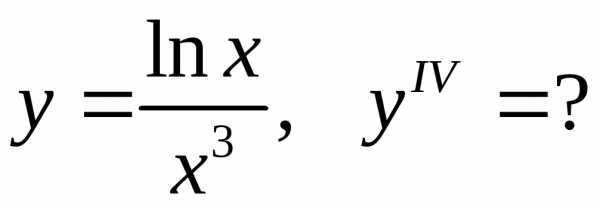 18.12.
18.12.
18.13. 18.14.
18.15. 18.16.
18.17. 18.18.
18.19. 18.20.
18.21. 18.22.
18.23. 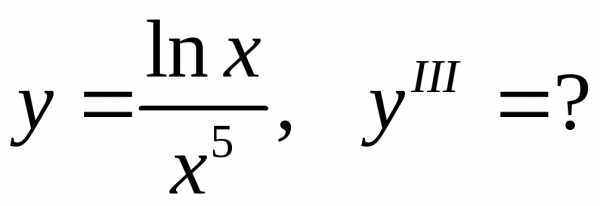 18.24.
18.24.
18.25. 18.26.
18.27. 18.28.
18.29. 18.30.
18.31.
studfiles.net
Производные(задачи)
II. ДИФФЕРЕНЦИРОВАНИЕ
Понятие производной. Производная функции
 .
.Геометрический смысл производной. Уравнения касательной и нормали к графику функции.
Понятие дифференцируемости функции и дифференциала. Условие дифференцируемости. Связь дифференциала с производной.
Геометрический смысл дифференциала.
Непрерывность дифференцируемой функции.
Дифференцирование постоянной и суммы, произведения и частного.
Производная сложной функции.
Инвариантность формы дифференциала.
Производная обратной функции.
Производные обратных тригонометрических функций.
Задача 5. Найти производную.
5.1.5.2.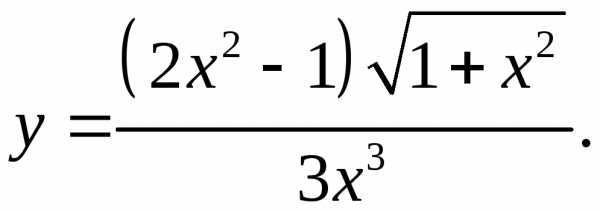
5.3. 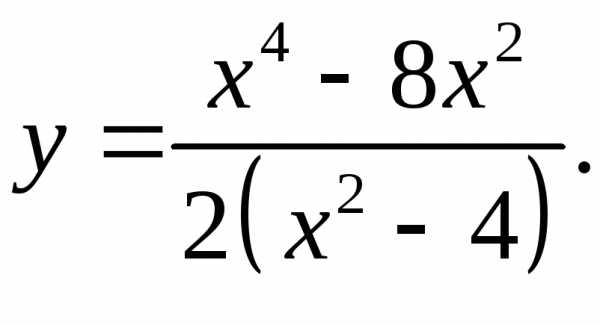 5.4.
5.4.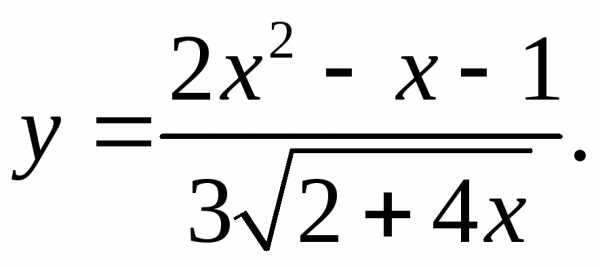
5.5. 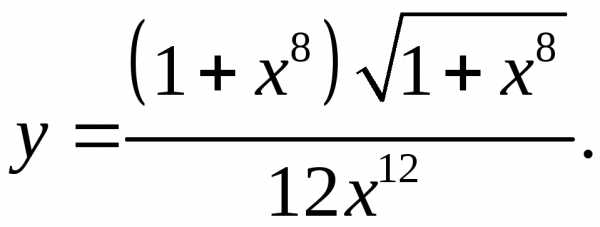 5.6.
5.6.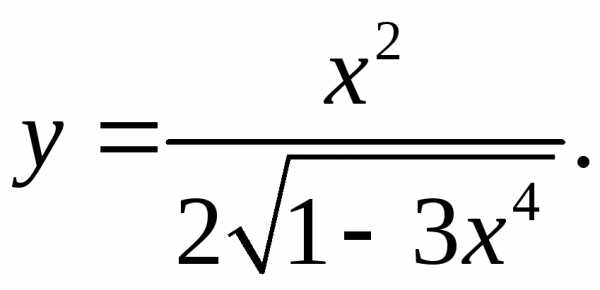
5.7. 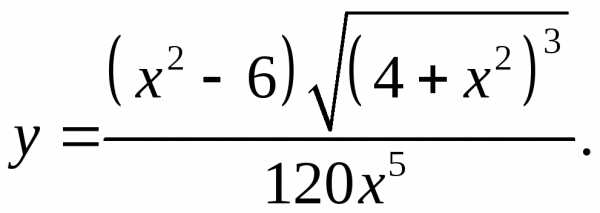 5.8.
5.8.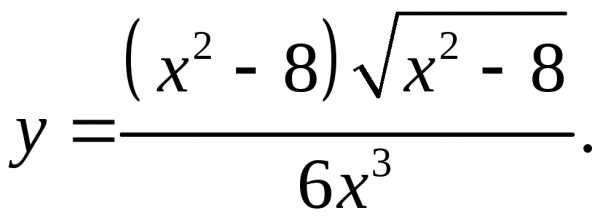
5.9. 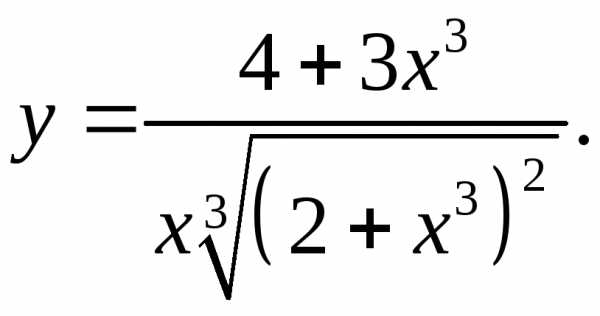 5.10.
5.10.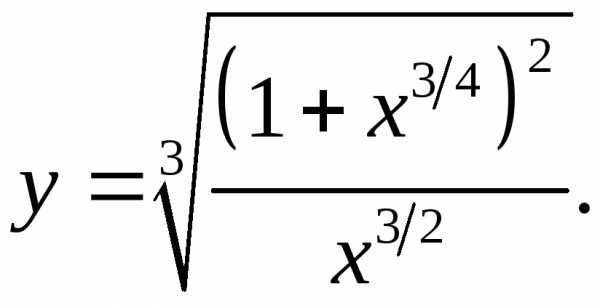
5.11. 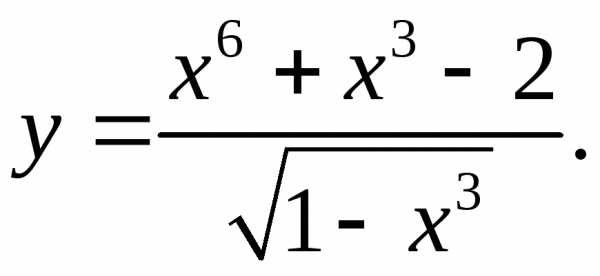 5.12.
5.12.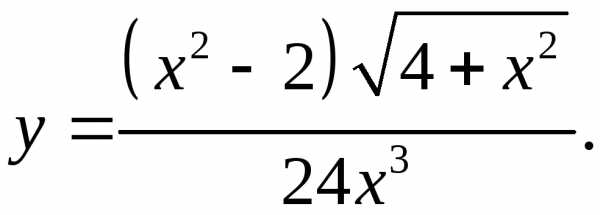
5.13. 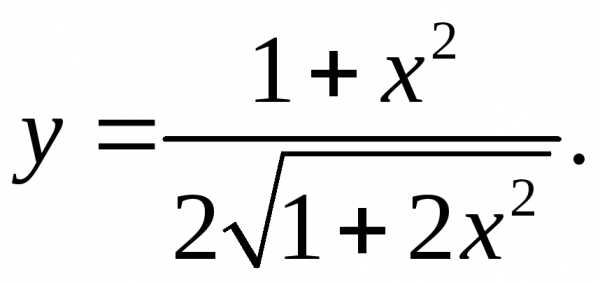 5.14.
5.14.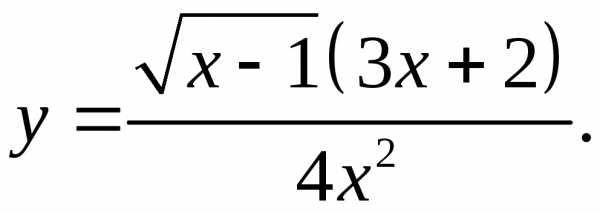
5.15. 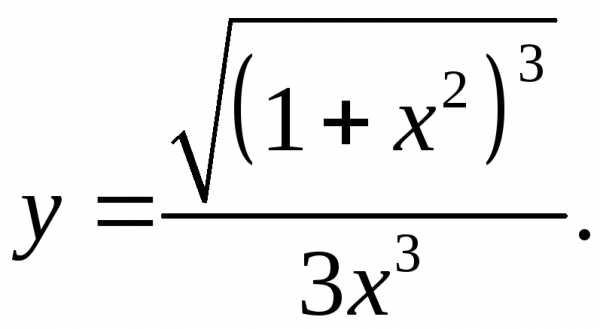 5.16.
5.16.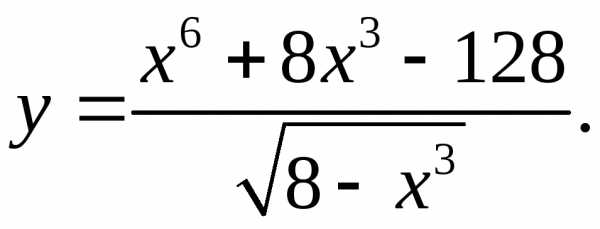
5.17. 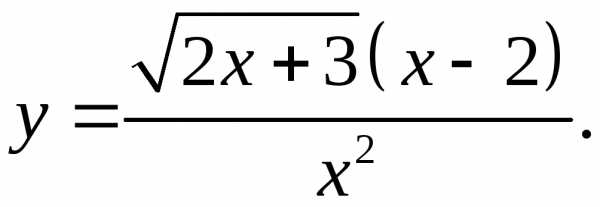 5.18.
5.18.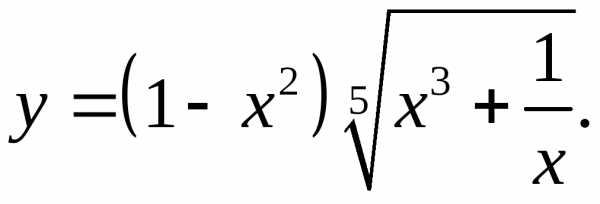
5.19. 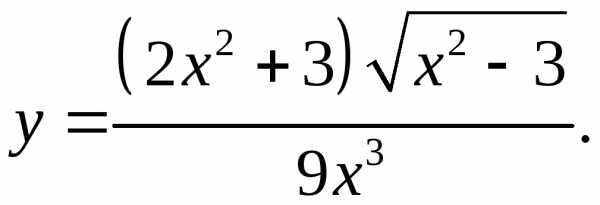 5.20.
5.20.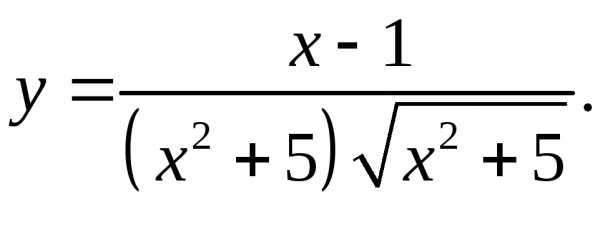
5.21. 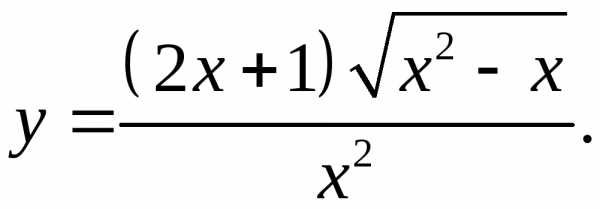 5.22.
5.22.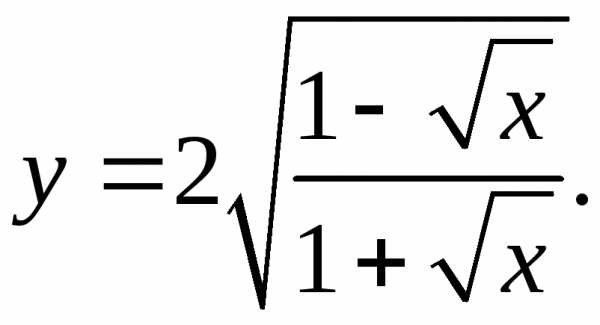
5.23.
5.24.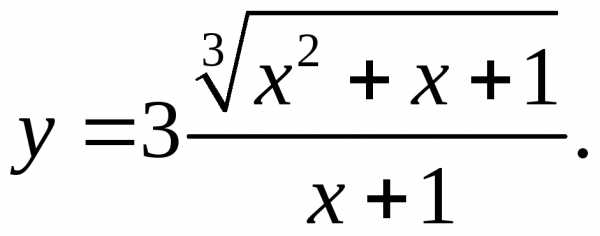
5.25. 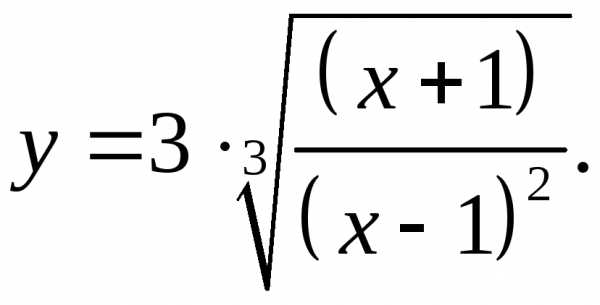 5.26.
5.26.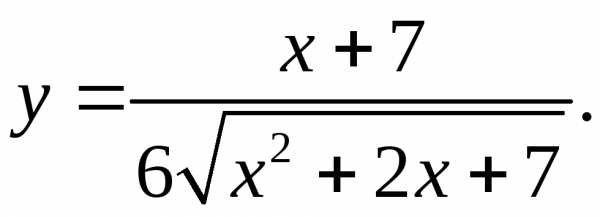
5.27. 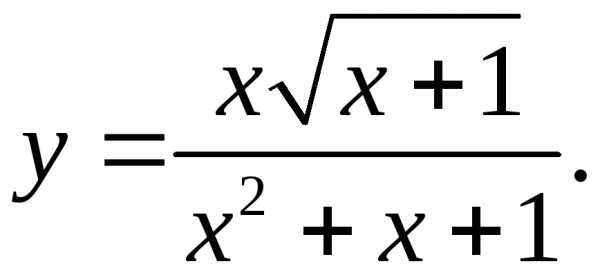 5.28.
5.28.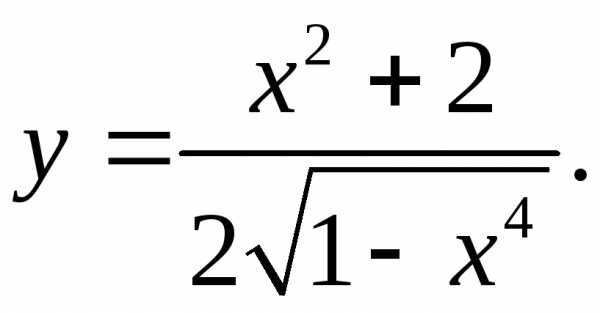
5.29. 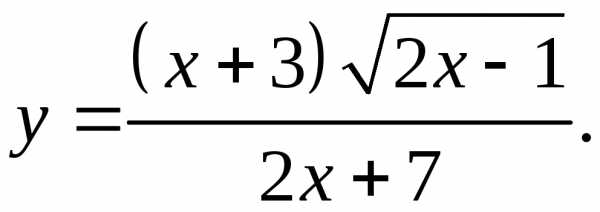 5.30.
5.30.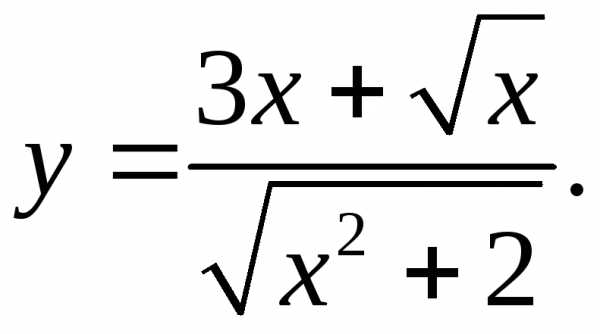
5.31.
Задача 6. Найти производную.
6.1. 6.2.
6.3. 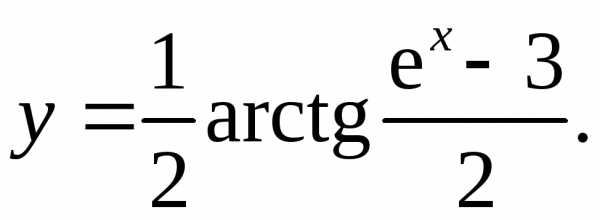 6.4.
6.4. 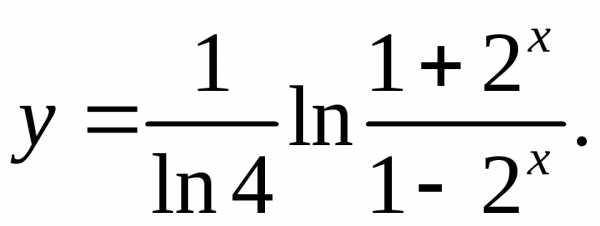
6.5. 6.6.
6.7. 6.8.
6.9. 6.10.
6.11. 6.12.
6.13.
6.14.
6.15.
6.16. 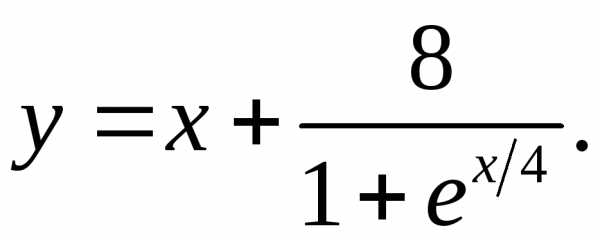
6.17.
6.18.
6.19.
6.20. 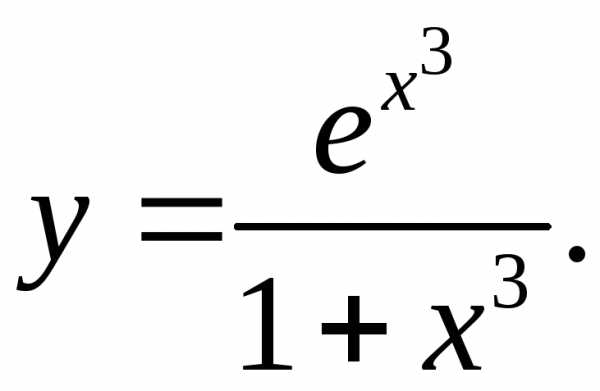
6.21. 6.22.
6.23. 6.24.
6.25.
6.26.
6.27.
6.28. 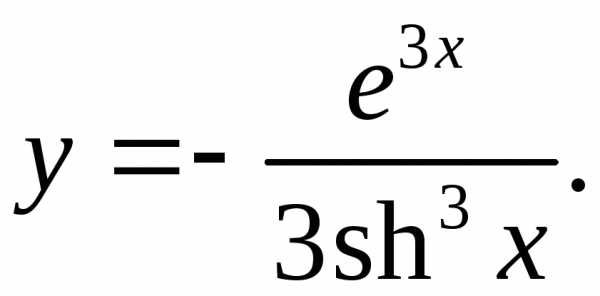
6.29. 6.30.
6.31. 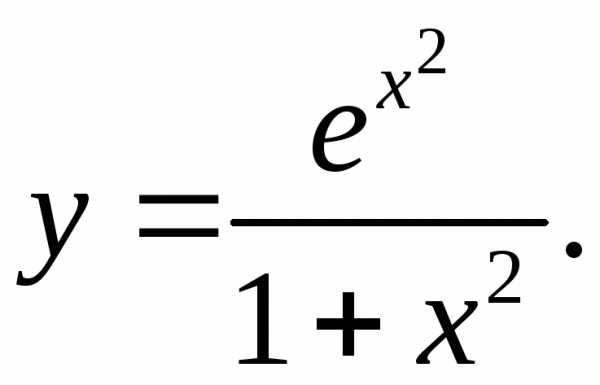
Задача 8. Найти производную.
8.1. 8.2.
8.3. 8.4.
8.5. 8.6.
8.7. 8.8.
8.9. 8.10.
8.11. 8.12.
8.13. 8.14.
8.15. 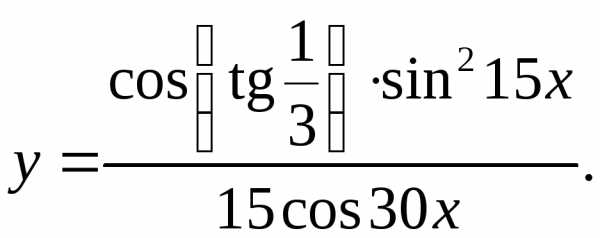 8.16.
8.16.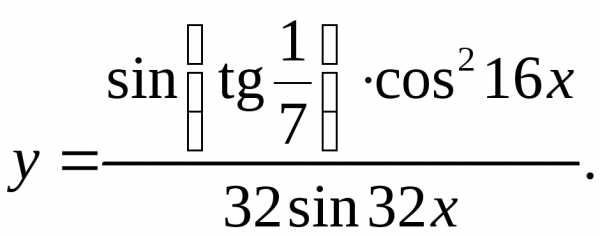
8.17. 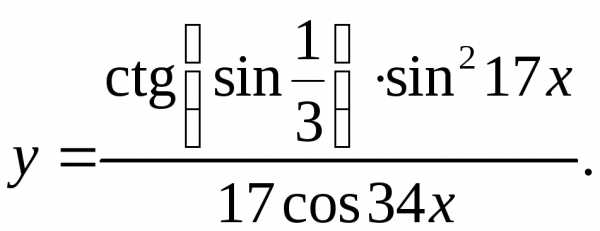 8.18.
8.18.
8.19. 8.20.
8.21. 8.22.
8.23. 8.24.
8.25. 8.26.
8.27. 8.28.
8.29. 8.30.
8.31.
Задача 9. Найти производную.
9.1.
9.2.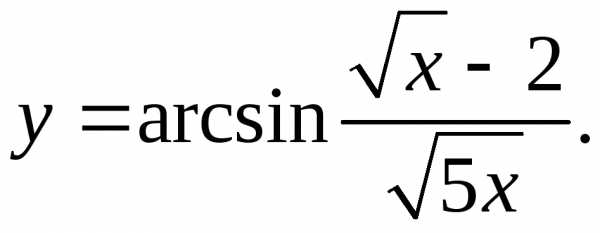
9.3.
9.4.
9.5. 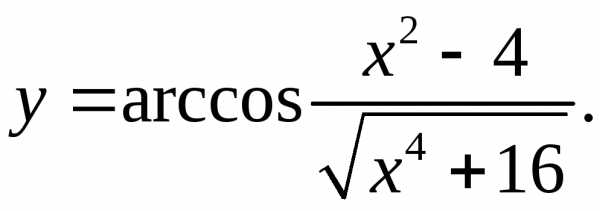 9.6.
9.6.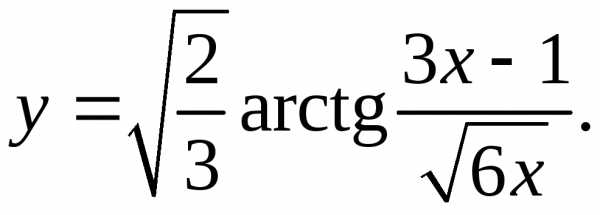
9.7.
9.8.
9.9. 9.10.
9.11. 9.12.
9.13. 9.14.
9.15. 9.16.
9.17.
9.18.
9.19.
9.20.
9.21.
9.22.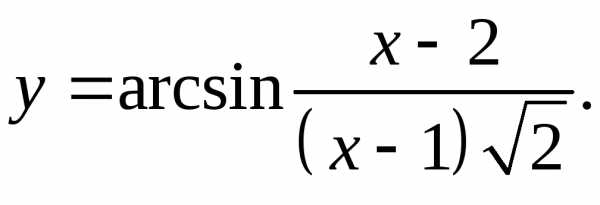
9.23. 9.24.
9.25. 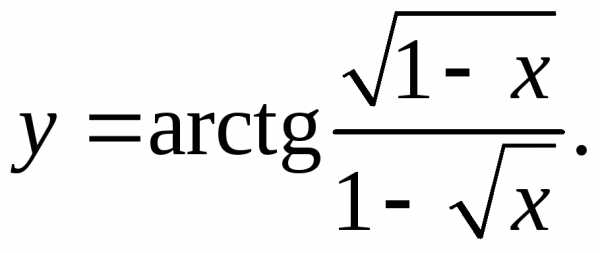 9.26.
9.26.
9.27.
9.28.
9.29.
9.30.
9.31.
Задача
17. Найти
производную 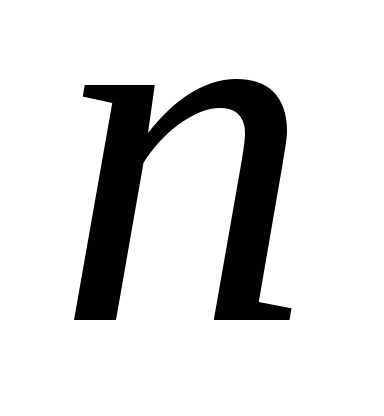 -го
порядка.
-го
порядка.
17.1. 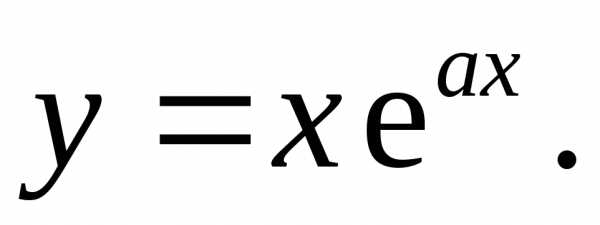 17.2.
17.2.
17.3. 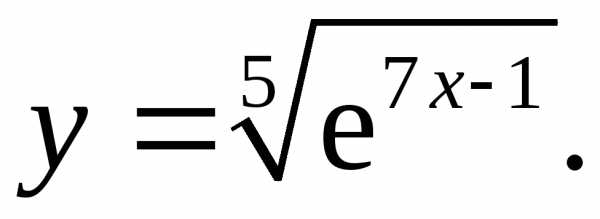 17.4.
17.4.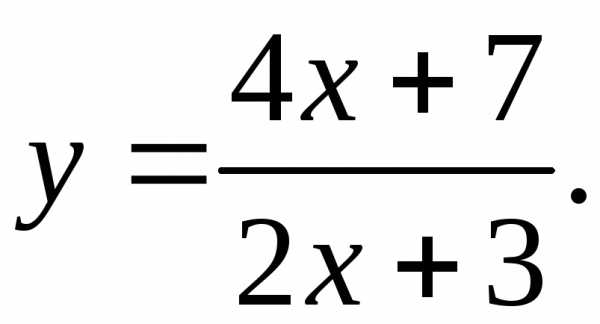
17.5.
17.6.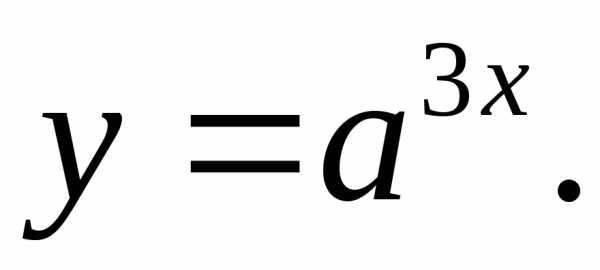
17.7. 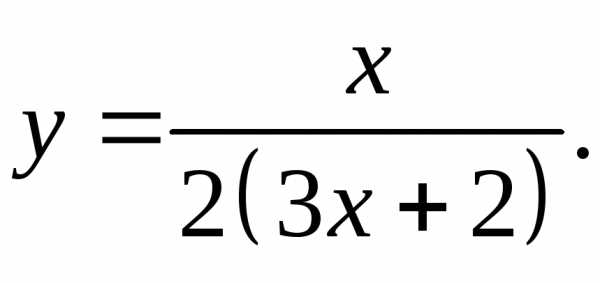 17.8.
17.8.
17.9. 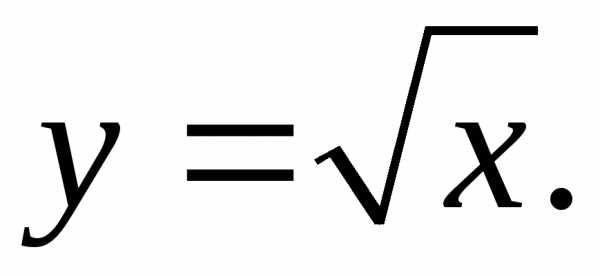 17.10.
17.10.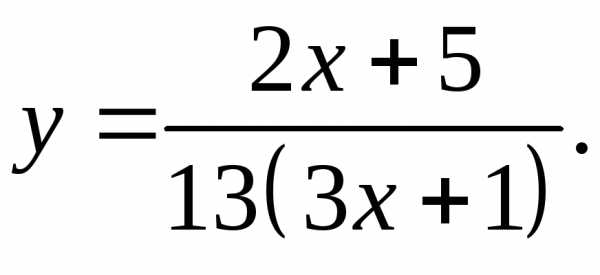
17.11. 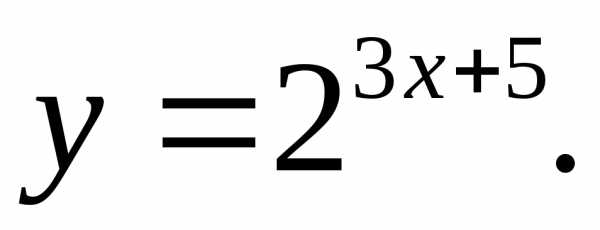 17.12.
17.12.
17.13. 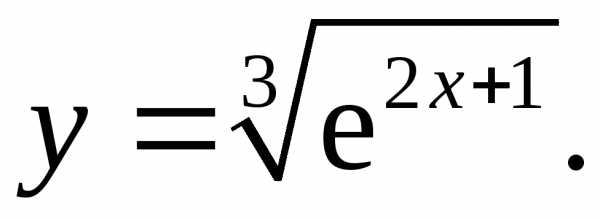 17.14.
17.14.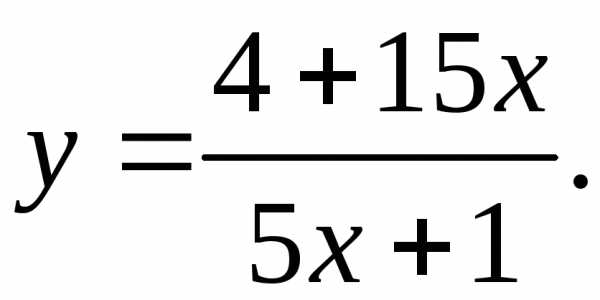
17.15.
17.16.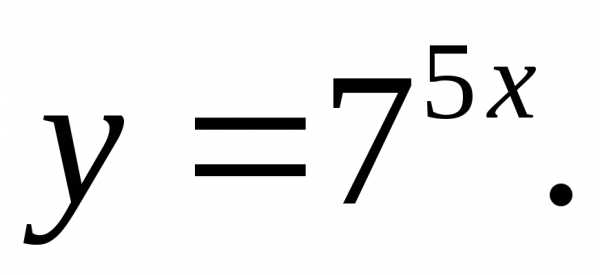
17.17. 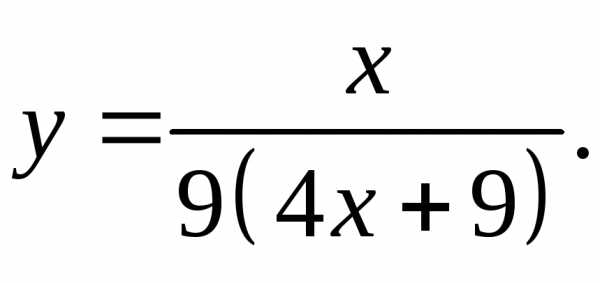 17.18.
17.18.
17.19. 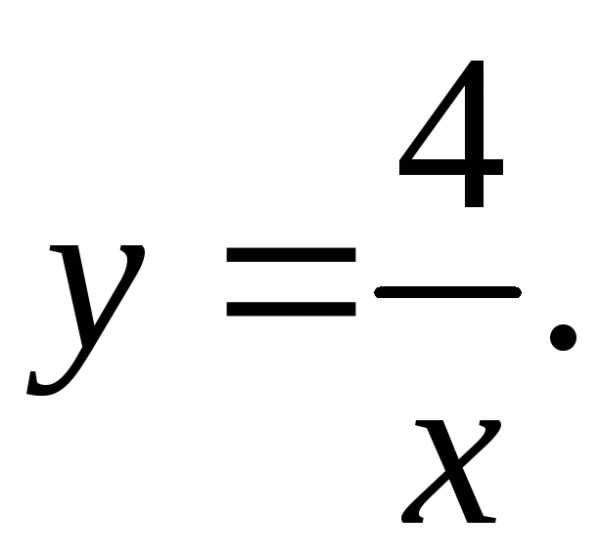 17.20.
17.20.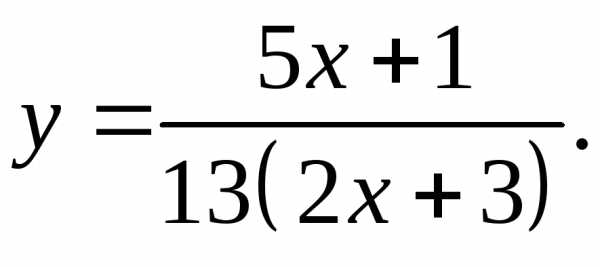
17.21. 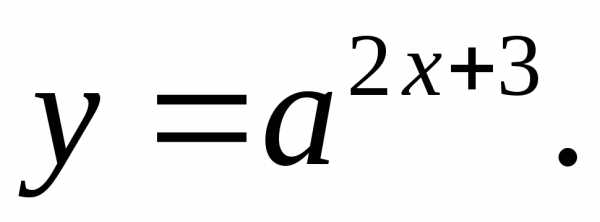 17.22.
17.22.
17.23. 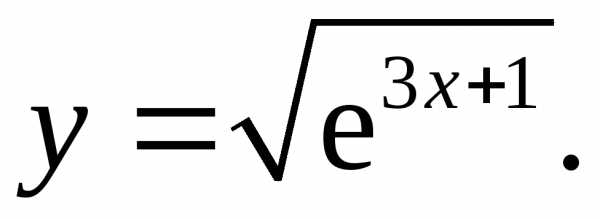 17.24.
17.24.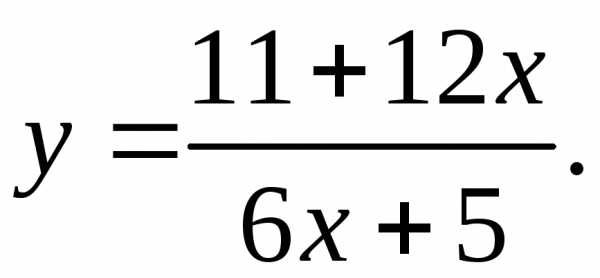
17.25.
17.26.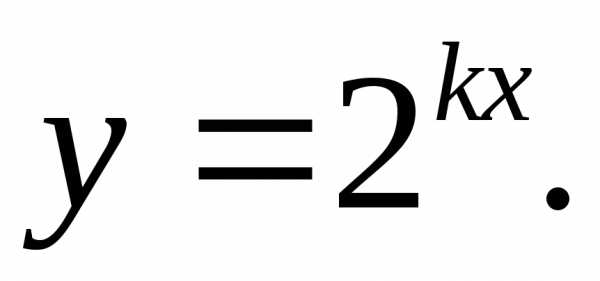
17.27. 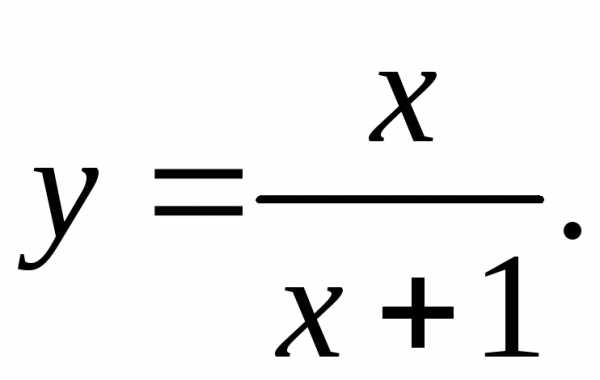 17.28.
17.28.
17.29. 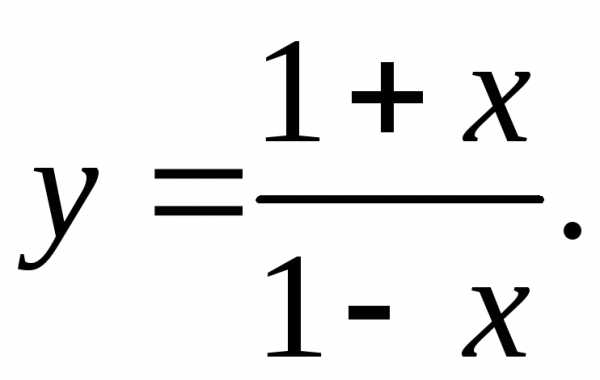 17.30.
17.30.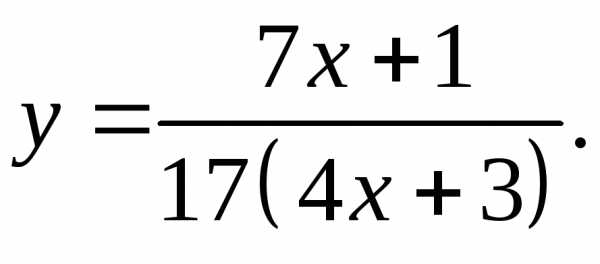
17.31. 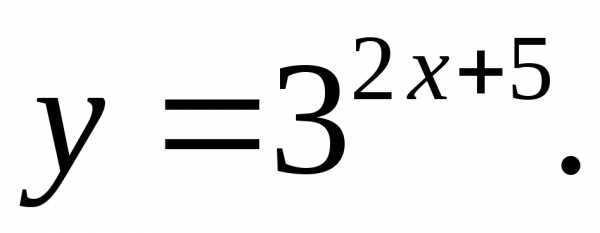
Задача 18. Найти производную указанного порядка.
18.1. 18.2.
18.3. 18.4.
18.5. 18.6.
18.7.
18.8.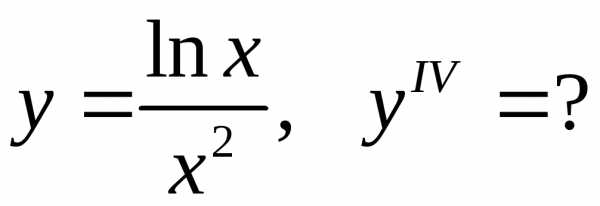
18.9. 18.10.
18.11. 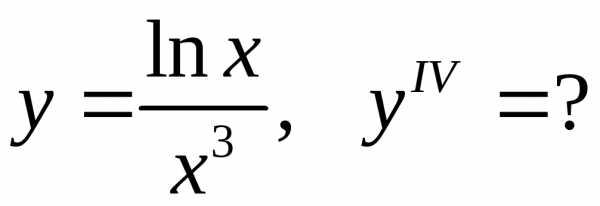 18.12.
18.12.
18.13. 18.14.
18.15. 18.16.
18.17. 18.18.
18.19. 18.20.
18.21. 18.22.
18.23. 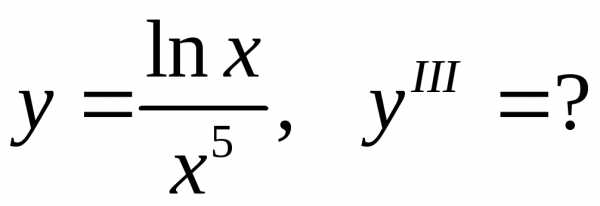 18.24.
18.24.
18.25. 18.26.
18.27. 18.28.
18.29. 18.30.
18.31.
studfiles.net
2.3.6. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ «Производные высших порядков»
Задача 1.
Найти вторую производную от функции
Указание
Найдите вначале первую производную данной функции, а затем воспользуйтесь тем, что
Решение
Ответ:
Задача 2.
Найти вторую производную от функции
При Х = 1.
Указание
Найдите вторую производную по формуле
А затем вычислите ее значение при Х = 1.
Решение
Ответ:
Задача 3.
Найти производную 4-го порядка от функции
Указание
Воспользуйтесь тем, что
Решение

Ответ:
Задача 4.
Найдите общее выражение для производной порядка П от функции
Указание
Воспользуйтесь тем, что
Решение
Вычислим подряд производные 1-го, 2-го, … порядка от данной функции и попробуем определить вид зависимости выражения для П-й производной от ее порядка.
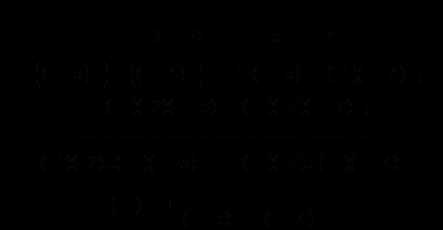
Ответ:
Задача 5.
Найдите общее выражение для производной порядка П от функции
Указание
Для упрощения воспользуйтесь формулами приведения:
Решение

Ответ:
Задача 6.
Найти вторую производную для функции, заданной параметрически:
Указание
Воспользуйтесь формулой
Решение
Ответ:
Задача 7.
Найти D3Y для функции У = Х5.
Указание
Воспользуйтесь формулой
Решение
Ответ:
Задача 8.
Вычислите производную:
Указание
Воспользуйтесь формулой Лейбница:
Решение
Пусть
Тогда
Применяя формулу Лейбница, получим:
Ответ:
Задача 9.
Рассматриваются функции
Для какой из них выполнены все условия теоремы Ролля?
Указание
По условию теоремы Ролля функция Y = F(X)
4) непрерывна на отрезке [Ab];
5) дифференцируема во всех внутренних точках этого отрезка;
6) принимает равные значения на концах этого отрезка, то есть F(A) = F(B).
Решение
Проверим выполнение условий теоремы Ролля для каждой из функций:
Не выполнено 3-е условие теоремы Ролля;
Эта функция не дифференцируема при Х = 1, то есть не выполнено 2-е условие теоремы Ролля;
3) Х = 0 – точка разрыва данной функции, то есть не выполнено 1-е условие теоремы Ролля;
Функция Y = ln cos X определена и непрерывна на заданном отрезке;
Существует на всем отрезке;
Таким образом, все условия теоремы Ролля выполнены.
Функция не является непрерывной в точке Х = 1, не выполнено 1-е условие теоремы Ролля.
Ответ: 4.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
1.Задачи ,приводящие к понятию производной:
а)о скорости движения материальной точки
б) об угле наклона касательной к графику функции
А.Пусть некоторая материальная точка совершает прямолинейное движение. В момент времени t1 точка находится в положении М1. В момент времени t2 в положении М2. Обозначим промежуток М1,М2 через S ; t2-t1= t. Величина S/ t называется средней скоростью движения. Чтобы найти мгновенную скорость точки в положении М1 необходимо t устремить к нулю. Математически это значит , что
,
Таким образом , для нахождения мгновенной скорости материальной точки необходимо вычислить предел отношения приращения функции S к приращению аргумента t при условии ,что t →0
Б.
Пусть (t)
есть количество вещества прореагировавшего
за время t.
Спустя время  количество
прореагировавшего вещества будет
количество
прореагировавшего вещества будет 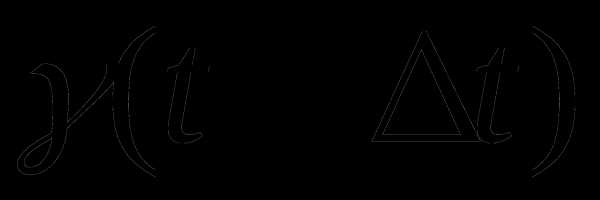 ,
т.е. за время
,
т.е. за время  количество
прореагировавшего вещества .
Поэтому средняя скорость химической
реакции за интервал времени
количество
прореагировавшего вещества .
Поэтому средняя скорость химической
реакции за интервал времени  будет
равна
будет
равна  .
Чтобы найти мгновенную скорость
химической реакции в момент времени
.
Чтобы найти мгновенную скорость
химической реакции в момент времени  надо
устремить
надо
устремить  к
нулю, то есть
к
нулю, то есть
.
Таким образом, производная от количества прореагировавшего вещества определяет мгновенную скорость химической реакции.
Пусть
функция определена
на промежутке X,
точка 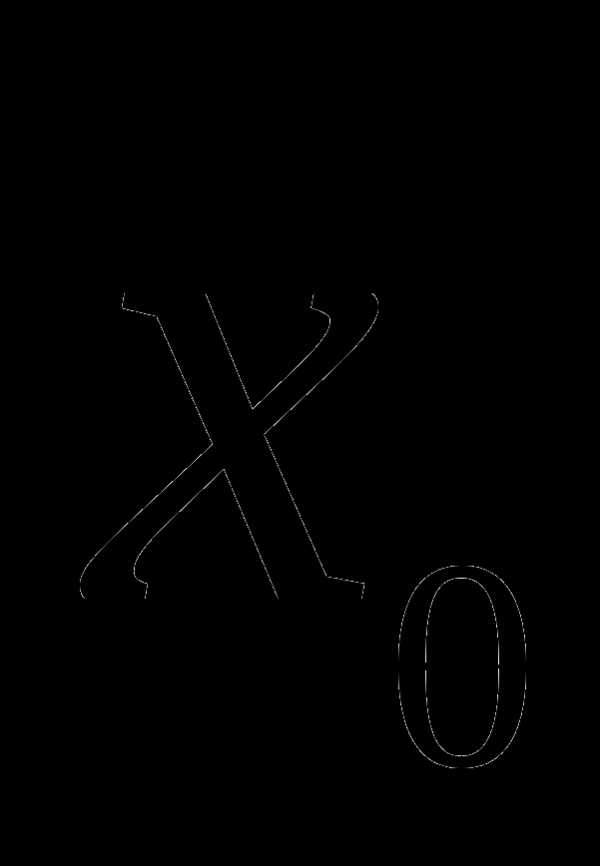 X,
дадим ей приращение ,
величина
X,
дадим ей приращение ,
величина 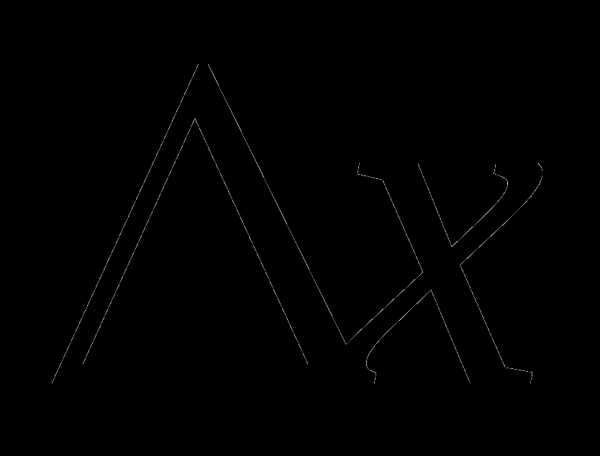 называется
приращением аргумента. В каждой из этих
точек посчитаем значение функции
называется
приращением аргумента. В каждой из этих
точек посчитаем значение функции 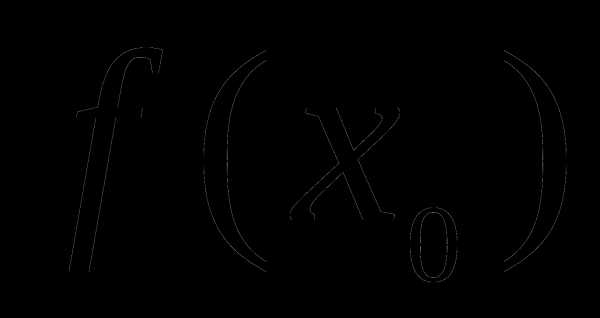 и .
Тогда можно говорить о приращении
функции .
и .
Тогда можно говорить о приращении
функции .
2.Производная функции.Геометрический и механический смыслы производной.Производные основных элементарных функций.Производная сложной функции.
Производной функции у=ƒ(х) β точке х0 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Итак, по определению
Производная функции ƒ(х) есть некоторая функция f'(x), произведённая из данной функции.
Функция у=ƒ(х), имеющая производную в каждой точке интервала (a;b), называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.
Значение производной функции у=ƒ(х) в точке х=х0 обозначается одним из символов: ƒ'(х0), у’|x=xo или у'(х0).
Геометрический смысл производной. Рассмотрим график функции y = f ( x ):
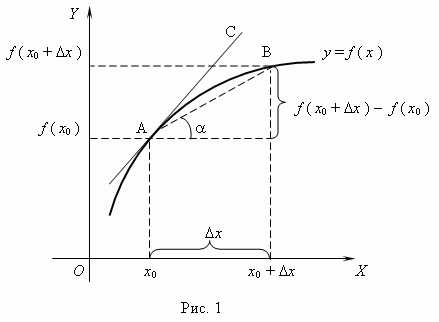
видно, что для любых двух точек A и B графика функции:
где – угол наклона секущей AB.
Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.
Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x ( t ) времени t. В течение интервала времени от t0 до t0 + точка перемещается на расстояние: x ( t0 + ) – x ( t0 ) = , а её средняя скорость равна: va = / . При 0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v ( t0 ) материальной точки в момент времени t0 . Но по определению производной мы имеем:
отсюда, v ( t0 ) = x’ ( t0 ) , т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной.Аналогично, ускорение – это производная скорости по времени: a = v’ ( t ).

studfiles.net
Простейшие типовые задачи с производной. Примеры решений
После изучения азов нахождения производной в статьях Как найти производную? Примеры решений иПроизводная сложной функции мы рассмотрим типовые задачи, связанные с нахождением производной. Желающие улучшить свои навыки дифференцирования также могут ознакомиться с урокомСложные производные. Логарифмическая производная.
Помимо нового материала у вас есть возможность дополнительно «набить руку» на нахождении производных. Действительно, если речь пойдет о типовых задачах на производную, то, как минимум, во всех примерах нужно будет найти эту самую производную. Я постараюсь рассмотреть приёмы решения и хитрости, которые не встречались в других статьях.
Вот наше аппетитное меню:
Производная функции в точке Уравнение касательной к графику прямой
Дифференциал функции одной переменной Вторая производная
Повар на раздаче.
Производная функции в точке
Как найти производную функции в точке? Из формулировки следуют два очевидных пункта этого задания:
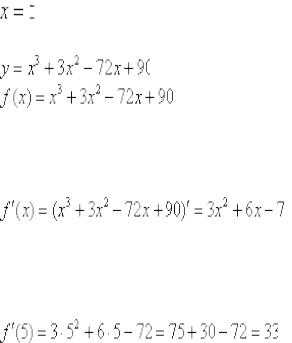
1)Необходимо найти производную.
2)Необходимо вычислить значение производной в заданной точке. Пример 1
Вычислить производную функции в точке
Справка: Следующие способы обозначения функции эквивалентны:
В некоторых заданиях бывает удобно обозначить функцию «игреком», а в некоторых через «эф от икс».
Сначала находим производную:
Надеюсь, многие уже приноровились находить такие производные устно.
На втором шаге вычислим значение производной в точке :
Готово.
Небольшой разминочный пример для самостоятельного решения:
Пример 2
Вычислить производную функции в точке
Полное решение и ответ в конце урока.
Необходимость находить производную в точке возникает в следующих задачах: построение касательной к графику функции
(следующий параграф), исследование функции на экстремум, исследование функции на перегиб графика, полное исследование функции и др.
Но рассматриваемое задание встречается в контрольных работах и само по себе. И, как правило, в таких случаях функцию дают достаточно сложную. В этой связи рассмотрим еще два примера.
Пример 3
Вычислить производную функции
в точке .
Сначала найдем производную:
Производная, в принципе, найдена, и можно подставлять требуемое значение . Ночто-тоделать это не сильно хочется. Выражение
очень длинное, да и значение «икс» у нас дробное. Поэтому стараемся максимально упростить нашу производную. В данном случае попробуем привести к общему знаменателю три последних слагаемых:
studfiles.net
Задания для самостоятельного решения
Понятие производной.
Правила дифференцирования. Таблица производных
Пусть определена в точке и в некоторой ее окрестности.
Пусть точка рассматриваемой окрестности, то приращением аргумента в точке называется величина , приращением функции – величина . Если выразить , то .
Производной функции в точке называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, при условии, что предел существует.
Производную в точке обозначают . По определению
, (1)
или, что то же,
, (2)
при условии, что пределы (1),(2) существуют.
Функция, имеющая производную в точке, называется дифференцируемой в этой точке. Операция нахождения производной называется дифференцированием.
Производная функции в точке – это число. Если функция дифференцируема на некотором множестве X из ее области определения, то также является функцией (ее обозначают также ).
Основные правила дифференцирования
Пусть -дифференцируемые функции. Справедливы формулы:
; (3)
; (4)
; (5)
; (6)
. (7)
Таблица производных основных элементарных функций
1) ,где ,
в частности
а) ,
б) ;
2) где ,
в частности
;
3) где ,
в частности
;
4) ;
5) ;
6) ;
7) ;
8) ;
9) ;
10) ;
11) ;
12) ;
13) ;
14) ;
15) .
Пример 1: Найти производную функции в точке , пользуясь определением, если:
1) , ;
2) .
Решение. 1.Используем определение производной в виде формулы (1):
Поскольку по условию , то
2. По формуле (1) получаем
Далее, применив тригонометрическую формулу , получим:
Так как при имеем и, применив формулу первого замечательного предела, получаем:
Поскольку по условию , то
Пример 2:Вычислить производную функции , пользуясь определением производной.
Решение.Пусть произвольная фиксированная точка из . Пользуясь формулой (1), имеем:
Таким образом, операция дифференцирования ставит в соответствие функции , функцию .
Пример 3.Найти производную функции:
1) ;
2) ; 3) .
Решение. 1. Дифференцируем функцию и используем формулы (4), (5) и таблицу производных, получаем:
2. Дифференцируем функцию по формулам (3), (4), (6) и соответствующим формулам таблицы производных:
3. Дифференцируем функцию по формулам (7), (5), (3) и первой формуле таблицы производных:
Пример 4. Вычислить производную функции, используя правила дифференцирования и таблицу производных:
1) 2) ;
3)
Решение.1. Преобразуем функцию, пользуясь свойствами логарифма:
Полученное выражение дифференцируем по формулам (4), (5), (6) и формулам таблицы производных:
2. Перед дифференцированием преобразуем выражение, пользуясь свойствами логарифма:
Дальше воспользуемся формулами (3), (4), (5) и таблицей производных:
3. Так как непосредственное дифференцирование вызывает значительные трудности, предварительно упростим выражение по формулам тригонометрии:
Полученное выражение дифференцируем по формуле (7) и соответствующим формулам таблицы производных.
Задания для самостоятельного решения
I уровень
1.1.Пользуясь определением, найдите производную функции:
1) 2)
1.2.Найдите производную функции:
1) ; 2) ;
3) ; 4) ;
5) ; 6) ;
7) ; 8) .
1.3. Найдите , если
1) ; 2) ;
3) ; 4) ;
5) ; 6) .
1.4.Вычислите:
1) , если: ;
2) если
;
3) если .
1.5. Вычислите , если
1.6.Вычислите , если .
1.7. Решите уравнение:
1) , где
2) , где .
II уровень
2.1. Найдите производные , предварительно преобразовав выражение:
1) ; 2) ;
3) ; 4) .
2.2. Для функции найдите
2.3.Известно, что . Найдите .
2.4. Решите неравенство , где .
III уровень
3.1. Вычислите , если:
1) ,
2) , .
3.2. Пользуясь определением производной, найдите , где
3.3. Найдите значение производной функции в точке , если .
3.4.Найдите сумму значений производной функции в точках x = 1 и x = 0.
Похожие статьи:
poznayka.org

 .
. .
.

