08.05.201919.11.2018

Закон ома для неполного участка цепи – Закон ома для участка цепи и для полной цепи / Школа электрика / Коллективный блог

• by alexxlab
• Комментариев к записи Закон ома для неполного участка цепи – Закон ома для участка цепи и для полной цепи / Школа электрика / Коллективный блог нет
• Советы абитуриенту

Закон ома для участка цепи и для полной цепи / Школа электрика / Коллективный блог

Закон Ома – физический закон, который определяет связь между электродвижущей силой источника и напряжением с силой электротока и сопротивляемостью проводника. Экспериментально был доказан в далеком 1826 году и назван в честь его первооткрывателя физика Георга Ома.

Закон Ома для участка цепи:

Немецким физиком Георгом Омом в 1826 году было обнаружено, что отношение напряжения между концами проводника сделанного из металла, который является участком электроцепи, к силе тока в цепи является постоянной величиной:

U / I = R = const.

Эта величина R называется электросопротивлением проводника. Электрическое сопротивление измеряют в Омах.

Электрическое сопротивление в 1Ом имеет такой участок цепи, на котором при силе тока равной 1А, напряжение будет ровняться 1В:

1 Ом = 1 В / 1 А.

Опыт показывается, что электросопротивление проводника прямо пропорционально его длине и обратно пропорционально его площади поперечного сечения:

R = r • L / S.

Параметр r называется электрическим сопротивлением вещества. Удельное сопротивление веществ измеряют в Ом • м.

Закон Ома для полной цепи:

Закон Ома для полной цепи определяется значениями тока в реальной электрической цепи, он зависит не только от сопротивления нагрузки, но и от сопротивления источника тока.

I=E/(r+R)

I – сила тока в цепи
E – ЭДС источника напряжения
r – внутреннее сопротивление источника напряжения
R – общее сопротивление всех внешних элементов цепи

Из закона Ома для полной цепи вытекают два следующих следствия:

1. При r меньше R сила тока в цепи будет обратно пропорциональной ее сопротивлению.
2. При r больше R сила тока от свойств внешней цепи зависеть не будет.

Также из него можно выразить значение ЭДС источника напряжения:
E=I(r+R)

Вложение	Размер
1.png	3.28 КБ
2.gif	5.49 КБ
3.jpg	20.64 КБ

44kw.com

Закон Ома для полной (замкнутой) цепи

Закон Ома для полной цепи определяет значение тока в реальной цепи, который зависит не только от сопротивления нагрузки, но и от сопротивления самого источника тока. Другое название этого закона – закон Ома для замкнутой цепи. Рассмотрим смысл закона Ома для полной цепи более подробно.

Потребители электрического тока (например, электрические лампы) вместе с источником тока образуют замкнутую электрическую цепь. На рисунке 1 показана замкнутая электрическая цепь, состоящая из автомобильного аккумулятора и лампочки.

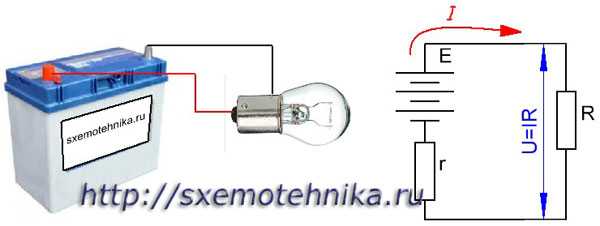
Рисунок 1. Замкнутая цепь, поясняющея закон Ома для полной цепи.

Ток, проходящий через лампочку, проходит также и через источник тока. Следовательно, проходя по цепи, ток кроме сопротивления проводника встретит еще и то сопротивление, которое ему будет оказывать сам источник тока (сопротивле­ние электролита между пластинами и сопротивление пограничных слоев электролита и пластин). Следовательно, общее сопротивление замкнутой цепи будет складываться из сопротивления лампочки и сопротивления источника тока.

Сопротивление нагрузки, присоединенной к источнику тока, принято называть внешним сопротивлением, а со­противление самого источника тока — внутренним со­противлением. Внутреннее сопротивление обозначается буквой r.

Если по цепи, изображенной на рисунке 1, протекает ток I, то для поддержания этого тока во внешней цепи согласно за­кону Ома между ее концами должна существовать раз­ность потенциалов, равная I*R. Но этот же ток I протекает и по внутренней цепи. Следовательно, для поддержания тока во внутренней цепи, также необходимо существование разности потенциалов между концами сопротивления r. Эта разность потенциалов па закону Ома должна быть равна I*r.

Поэтому для поддержания тока в цепи электродвижущая сила (ЭДС) аккумулятора должна иметь величину:

E=I*r+I*R

Эта формула показывает, что электродвижущая сила в цепи равна сумме внешнего и внутреннего падений напряжения. Вынося I за скобки, получим:

E=I(r+R)

или

I=E/(r+R)

Две последние формулы выражают закона Ома для полной цепи.

Закон Ома для полной замкнутой цепи формулируется так: сила тока в замкнутой цепи прямо пропорциональ­на ЭДС в цепи и обратно пропорциональ­на общему сопротивлению цепи.

Под общим со­противлением подразумевается сумма внешнего и внутреннего сопротивлений.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

www.sxemotehnika.ru

Т. Закон Ома — PhysBook

Закон Ома для замкнутой цепи

Замкнутая цепь (рис. 2) состоит из двух частей — внутренней и внешней. Внутренняя часть цепи представляет собой источник тока, обладающий внутренним сопротивлением r; внешняя — различные потребители, соединительные провода, приборы и т.д. Общее сопротивление внешней части обозначается R. Тогда полное сопротивление цепи равно r + R.

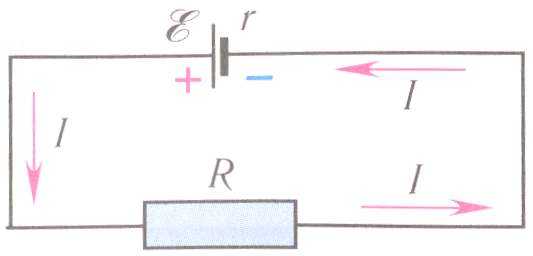
Рис. 2

По закону Ома для внешнего участка цепи 1 → 2 имеем:

\(~\varphi_1 – \varphi_2 = IR .\)

Внутренний участок цепи 2 → 1 является неоднородным. Согласно закону Ома, \(~\varphi_2 – \varphi_1 + \varepsilon = Ir\). Сложив эти равенства, получим

\(~\varepsilon = IR + Ir . \qquad (1)\)

Отсюда

\(~I = \frac{\varepsilon}{R + r} . \qquad (2)\)

Последняя формула представляет собой закон Ома для замкнутой цепи постоянного тока. Сила тока в цепи прямо пропорциональна ЭДС источника и обратно пропорциональна полному сопротивлению цепи.

Так как для однородного участка цепи разность потенциалов есть напряжение, то \(~\varphi_1 – \varphi_2 = IR = U\) и формулу (1) можно записать:

\(~\varepsilon = U + Ir \Rightarrow U = \varepsilon – Ir .\)

Из этой формулы видно, что напряжение на внешнем участке уменьшается с увеличением силы тока в цепи при ε = const.

Подставим в последнюю формулу силу тока (2), получим

\(~U = \varepsilon \left( 1 – \frac{r}{R + r} \right) .\)

Проанализируем это выражение для некоторых предельных режимов работы цепи.

а) При разомкнутой цепи (R → ∞) U = ε, т.е. напряжение на полюсах источника тока при разомкнутой цепи равно ЭДС источника тока.

На этом основана возможность приблизительного измерения ЭДС источника тока с помощью вольтметра, сопротивление которого много больше внутреннего сопротивления источника тока (\(~R_v \gg r\)). Для этого вольтметр подключают к клеммам источника тока.

б) Если к клеммам источника тока подключить проводник, сопротивление которого \(~R \ll r\), то R + r ≈ r, тогда \(~U = \varepsilon \left( 1 – \frac{r}{r} \right) = 0\) , а сила тока \(~I = \frac{\varepsilon}{r}\) — достигает максимального значения.

Подключение к полюсам источника тока проводника с ничтожно малым сопротивлением называется коротким замыканием, а максимальную для данного источника силу тока называют током короткого замыкания:

\(~I_{kz} = \frac{\varepsilon}{r} .\)

У источников с малым значением

r (например, у свинцовых аккумуляторов r = 0,1 – 0,01 Ом) сила тока короткого замыкания очень велика. Особенно опасно короткое замыкание в осветительных сетях, питаемых от подстанций (ε > 100 В), I_kz может достигнуть тысячи ампер. Чтобы избежать пожаров, в такие цепи включают предохранители.

Запишем закон Ома для полной цепи в случае последовательного и параллельного соединения источников тока в батарею. При последовательном соединении источников “-” одного источника соединяется с “+” второго, “-” второго с “+” третьего и т.д. (рис. 3, а). Если ε₁ = ε₂ = ε₃ а r₁ = r₂ = r₃ то ε_b = 3ε₁, r_b = 3r₁. В этом случае закон Ома для полной цепи имеет вид\[~I = \frac{\varepsilon_b}{R + r_b} = \frac{3 \varepsilon_1}{R + 3r_1}\], или для n одинаковых источников \(~I = \frac{n \varepsilon_1}{R + nr_1}\).

Рис. 3

Последовательное соединение применяют в том случае, когда внешнее сопротивление \(~R \gg nr_1\), тогда \(~I = \frac{n \varepsilon_1}{R}\) и батарея может дать силу тока, в n раз большую, чем сила тока от одного источника.

При параллельном соединении источников тока все “+” источников соединены вместе и “-” источников — также вместе (рис. 3, б). В этом случае

\(~\varepsilon_b = \varepsilon_1 ; \ r_b = \frac{r_1}{3}.\)

Откуда \(~I = \frac{\varepsilon_1}{R + \frac{r_1}{3}}\) .

Для n одинаковых источников \(~I = \frac{\varepsilon_1}{R + \frac{r_1}{n}}\) .

Параллельное соединение источников тока применяют тогда, когда нужно получить источник тока с малым внутренним сопротивлением или когда для нормальной работы потребителя электроэнергии в цепи должен протекать ток. больший, чем допустимый ток одного источника.

Параллельное соединение выгодно, когда R

невелико по сравнению с r.

Иногда применяют смешанное соединение источников.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 262-264.

www.physbook.ru

Закон Ома для неоднородного участка цепи

На практике видно, что для поддержания стабильного тока в замкнутой цепи необходимы силы принципиально иной природы, нежели кулоновские, тогда наблюдается случай, когда на участке цепи на свободные электрические заряды одновременно действуют как силы электрического поля, так и сторонние силы (любые неконсервативные силы, действующие на заряд, за исключением сил электрического сопротивления (кулоновских сил)). Такой участок называется неоднородным участком цепи. На рисунке ниже приведен пример такого участка.

Напряженность поля в любой точке цепи равна векторной сумме поля кулоновских сил и поля сторонних сил:

Сформулируем закон Ома для неоднородного участка цепи – Сила тока прямо пропорциональна напряжению на этом участке и обратно пропорциональна его полному сопротивлению:

– формула закона Ома для неоднородного участка цепи.

Где

• I – сила тока,
• U12 – напряжение на участке,
• R – полное сопротивление цепи.

Работа на неоднородном участке цепи

Разность потенциалов характеризует работу силы электрического поля по переносу единичного положительного заряда (q) из точки 1 в точку 2:

– где φ1 и φ 2 – потенциалы на концах участка.

ЭДС характеризует работу сторонних сил по переносу единичного положительного заряда точки 1 в точку 2: – где ε12 – ЭДС, действующая на данном участке, численно равна работе по перемещению единичного положительного заряда вдоль контура.

Напряжение на участке цепи представляет собой суммарную работу сил ЭП и сторонних сил:

Тогда закон Ома примет вид:

ЭДС может быть как положительной, так и отрицательной. Это зависит от полярности включения ЭДС в участок. Если внутри источника тока обход совершается от отрицательного полюса к положительному, то ЭДС положительная (см. рисунок). Сторонние силы при этом совершают положительную работу. Если же обход совершается от положительного полюса к отрицательному, то ЭДС отрицательная. Проще говоря, если ЭДС способствует движению положительных зарядов, то ε>0, иначе ε

Решение задач по закону ому для неоднородного участка цепи

Определить ток, идущий по изображенному на рисунке участку АВ. ЭДС источника 20 В, внутреннее сопротивление 1 Ом, потенциалы точек А и В соответственно 15 В и 5 В, сопротивление проводов 3 Ом.

Дано:	Решение:
ε = 20 В r = 1 Ом φ1 = 15 В φ2 = 5 В R = 3 Ом	Запишем закон Ома для неоднородного участка цепи – Считая, что точка А начало участка, а точка В – конец, возьмем ЭДС со знаком «минус» и, подставив исходные данные, получим Знак «минус» говорит о том, что ток идет от точки В к точке А, от точки с меньшим потенциалом к точке с большим, что обычно для источников тока. Ответ: –2,5 А

Два элемента соединены «навстречу» друг другу, как показано на рисунке. Определить разность потенциалов между точками А и В, если ε1 = 1,4 В, r1 = 0,4 Ом, ε2 = 1,8 В, r2 = 0,6 Ом.

Дано:	Решение:
ε1 = 1,4 В r1 = 0,4 Ом ε2 = 1,8 В r2 = 0,6 Ом	Запишем закон Ома для неоднородного участка цепи – Разобьём схему на два участка: АЕ2В и ВЕ1А. Тогда получим – для первого участка цепи, – для второго участка. Ток на участках один и тот же, то есть можем приравнять правые части уравнений. Знак «минус» показывает, что потенциал точки В выше, чем потенциал точки А. Ответ: -1,56 В.

zakon-oma.ru

Закон Ома для однородного участка цепи

Обязательным условием существования электрического тока является наличие электрического поля, для существования которого, в свою очередь, необходима разность потенциалов (напряжение). Ток будет направлен в сторону уменьшения потенциалов (на рисунке – влево), а свободные электроны будут двигаться в обратную сторону.

На концах участка проводника заданы потенциалы φ_1 и φ_2, причем φ_1>φ_2. Напряжение в таком случае можно найти по формуле:

В 1826 году Георг Ом, обобщив итоги опытов, показавших, что, чем больше напряжение на участке, тем больше сила тока, проходящего через него, получил зависимость, названную законом Ома. В ходе экспериментов Ом выявил, что различные проводники при одинаково заданном напряжении будут проводить ток по-разному, т.е., каждый проводник обладает различной мерой проводимости. Эту величину назвали электрическим сопротивлением.

Определеение Закона Ома для однородного участка цепи гласит: сила тока для однородного проводника на участке цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению проводника.

Формула закона Ома для однородного участка цепи

• I [А] – сила тока,
• U [В] – напряжение,
• R [Ом] – электрическое сопротивление.

Сопротивление – главная характеристика проводника. В зависимости от строения проводника, в них существует различное количество узлов кристаллической решетки и атомов примесей, взаимодействуя с которыми электроны замедляются.

Сопротивление будет зависеть от рода и размеров проводника:

где:

• P – удельное сопротивление проводника (табличная величина, характеризующая способность материала к сопротивлению).
• l [м] – длина проводника,
• S [мм2] – площадь поперечного сечения проводника.

Решение задачи по теме Закон Ома для однородного участка цепи

Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 1 мм2, если к концам провода приложено напряжение 8,5 В.

zakon-oma.ru

Обобщенный закон Ома.

Закон Ома выражаемый формулой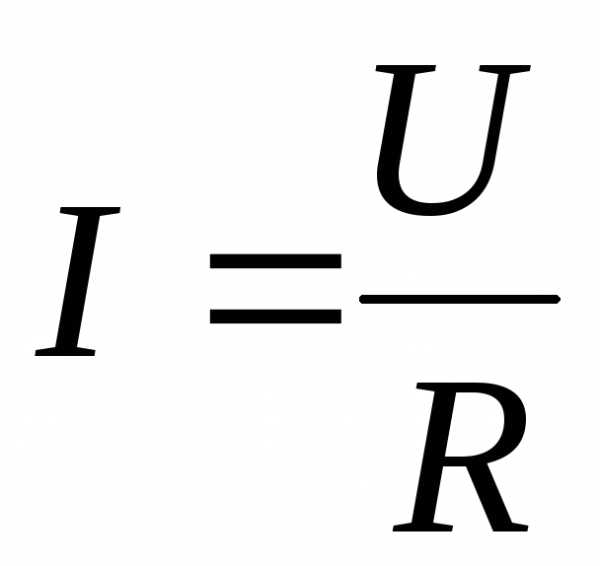, определяет зависимость между током и напряжением на пассивном участке электрической цепи.

Определим зависимость между током, напряжением и э.д.с. на активном участке (рис. 16).

Из формулы 15 следует:

_a-_b=I(R₁+R₂)- E₁+E₂ (16)

На положительное напряжение на участке a – b Uab=_a-_b

Следовательно, Uab= I(R₁+R₂)- E₁+E₂ (17)

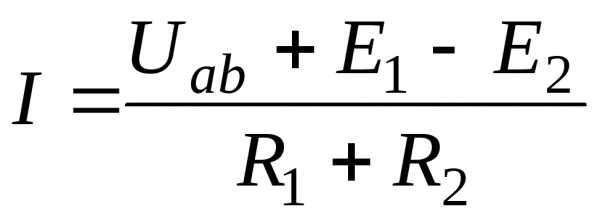(18)

Формула (18) выражает обобщенный закон Ома, или закон Ома для участка, содержащего э.д.с.

Из формулы видно, что если ток, напряжение и э.д.с. совпадают по направлению, то в выражение закона Ома они входят с одинаковыми знаками. Если э.д.с. действует в сторону, противоположную положительному направлению тока, то в выражении ставится знак «-».

Закон Ома применяется для участка ветви и для одноконтурной замкнутой схемы.

Пример № 1 построения потенциальной диаграммы:

Построить потенциальную диаграмму для одноконтурной схемы:

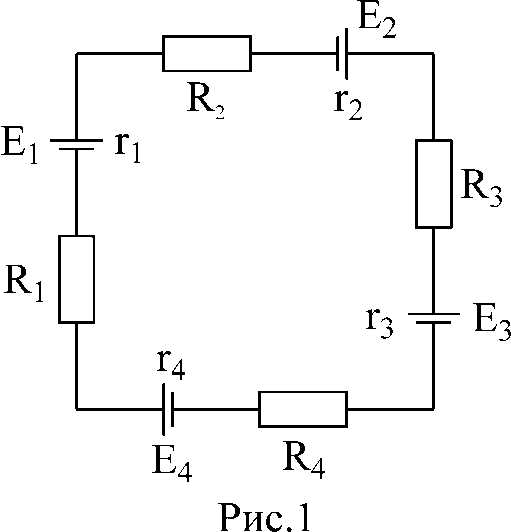
E₁=25В; E₂=5В; E₃=20В; E₄=35В,

R₁=8 Ом; R₂=24 Ом; R₃=40 Ом; R₄=4 Ом,

r₁=2 Ом; r₂=6 Ом; r₃=2 Ом; r₄=4 Ом.

Решение: 1. перерисуем заданный контур, вынося внутренние сопротивления э.д.с. (r₁– r₄) за их пределы; обозначим точки контура.

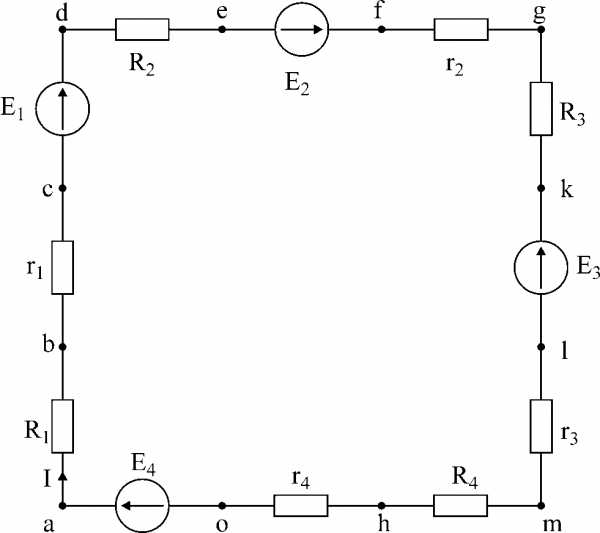
Рис.2

2. Выберем положительное направление тока I, определим его значение используя обобщенный закон Ома:

3. За базисную точку примем точку a. Найдем потенциалы остальных точек:

_b= _a– IR_{1 =} – 4В _e= _d– IR_{2 =} 8В

_c= _b– Ir_{1 =} – 5В _f= _e+ E_{2 =} 13В

_d= _c+ E_{1 =} 20В _q= _f– Ir_{2 =} 10В

_k= _q– IR_{3 =} – 10В _n= _m– IR_{4 =} – 33В

_e = _k – E_{3 =} – 30В _o = _n – Ir_{4 =} – 35В

_m = _e – Ir_{3 =} – 31В _a = _o + E_{4 =} 0

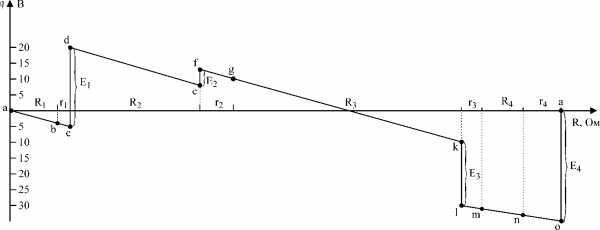
4. В системе координат строим потенциальную диаграмму:

Законы Кирхгофа.

Распределение токов по ветвям электрической цепи подчиняется первому закону Кирхгофа, а распределение напряжений по участкам цепи подчиняется второму закону Кирхгофа.

Законы Кирхгофа наряду с законом Ома являются основными в теории электрических цепей.

Первый закон Кирхгофа:

Алгебраическая сумма токов в узле равна нулю:

_i = 0 (19)

Где i – число ветвей, сходящихся в данном узле.

Т.е., суммирование распространяется на токи в ветвях, которые сходятся в рассматриваемом узле.

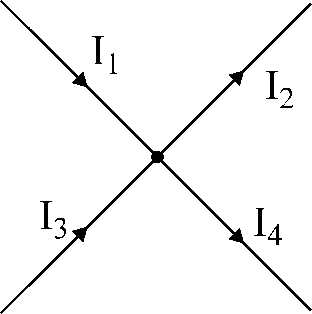
Рис.17. Иллюстрация к первому закону Кирхгофа.

Число уравнений, составляемых по первому закону Кирхгофа, определяется формулой:

Nуp = Nу – 1,

Где Nу – число узлов в рассматриваемой цепи.

Знаки токов в уравнении берутся с учетом выбранного положительного направления. Знаки у токов одинаковы, если токи одинаково ориентированы относительно данного узла.

Например, для узла, представленного на рис.17: припишем токам, подтекающим к узлу знаки «+», а к токам, оттекающим от узла – знаки «-».

Тогда уравнение по первому закону Кирхгофа запишется так:

I₁ – I₂ + I₃ – I₄ = 0.

Уравнения, составленные по первому закону Кирхгофа, называются узловыми.

Этот закон выражает тот факт, что в узле электрический заряд не накапливается и не расходуется. Сумма электрических зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла за один и тот же промежуток времени.

Второй закон Кирхгофа:

Алгебраическая сумма э.д.с. в любом замкнутом контуре цепи равна алгебраической сумме падений напряжения на элементах этого контура:

 Ui =  Ei

 IiRi=Ei(20)

Где i – номер элемента(сопротивления или источника напряжения) в рассматриваемом контуре.

**Число уравнений, составляемых по второму закону Кирхгофа, определяется формулой:

Nуp = Nb – Nу + 1 – Nэ.д.с.

Где Nb – число ветвей электрической цепи;

Nу – число узлов;

Nэ.д.с. – число идеальных источников э.д.с.

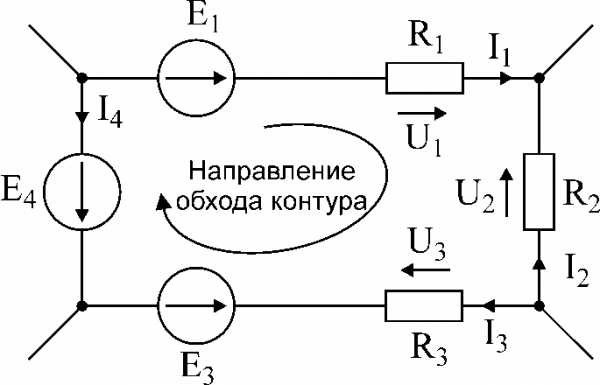
Рис.18. Иллюстрация ко второму закону Кирхгофа.

Для того, чтобы правильно записать второй закон Кирхгофа для заданного контура, следует выполнять следующие правила:

1. произвольно выбрать направление обхода контура, например, по часовой стрелке (рис.18).

2. э.д.с. и падения напряжения, которые совпадают по направлению с выбранным направлением обхода, записываются в выражении со знаком «+»; если э.д.с. и падения напряжения не совпадают с направлением обхода контура, то перед ними ставится знак «-».

Например, для контура рис.18, второй закон Кирхгофа запишется следующим образом:

U₁ – U₂ + U₃ = E₁ – E₃ – E₄ (21)

Уравнение (20) можно переписать в виде:

 (Ui – Ei) = 0 (22)

Где (U – E) – напряжение на ветви.

Следовательно, второй закон Кирхгофа можно сформулировать следующим образом:

Алгебраическая сумма напряжений на ветвях в любом замкнутом контуре равна нулю.

Потенциальная диаграмма, рассмотренная ранее, служит графической интерпретацией второго закона Кирхгофа.

Задача №1.

В схеме рис.1 заданы токи I₁ и I₃, сопротивления и э.д.с. Определить токи I₄, I₅, I₆ ; напряжение между точками a и b, если I₁ = 10мA, I₃ = -20 мA, R₄ = 5kОм, E₅ = 20B, R₅ = 3kОм, E₆ = 40B, R₆ = 2kОм.

.

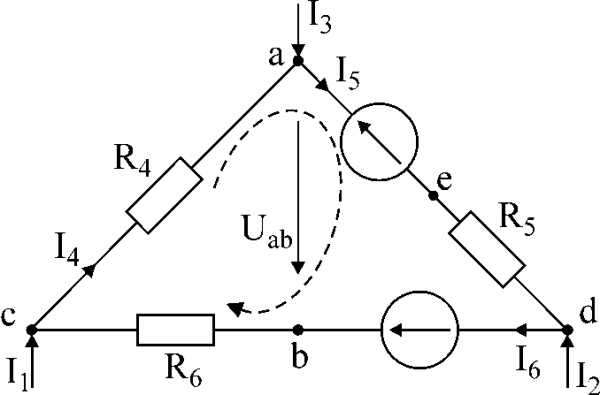
Рис.1

Решение:

1. Для заданного контура составим два уравнения по первому закону Кирхгофа и одно – по второму. Направление обхода контура указано стрелкой.

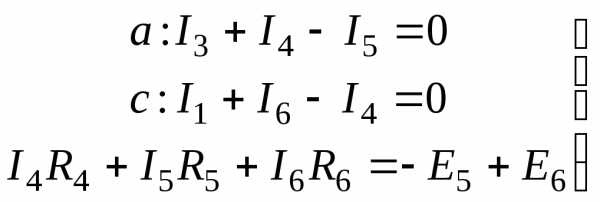
В результате решения получаем: I₆ = 0; I₄ = 10мA; I₅ = -10мA

2. зададим направление напряжения между точками a и b от точки «a» к точке «b» – U_ab. Это напряжение найдем из уравнения по второму закону Кирхгофа:

I₄R₄ + U_ab + I₆R₆ = 0

U_ab = – 50B.

Задача №2.

Для схемы рис.2 составить уравнения по законам Кирхгофа и определить неизвестные точки.

Дано: I₁ = 20мA; I₂ = 10мA

R₁ = 5kОм, R₃ = 4kОм, R₄ = 6kОм, R₅ = 2kОм, R₆ = 4kОм.

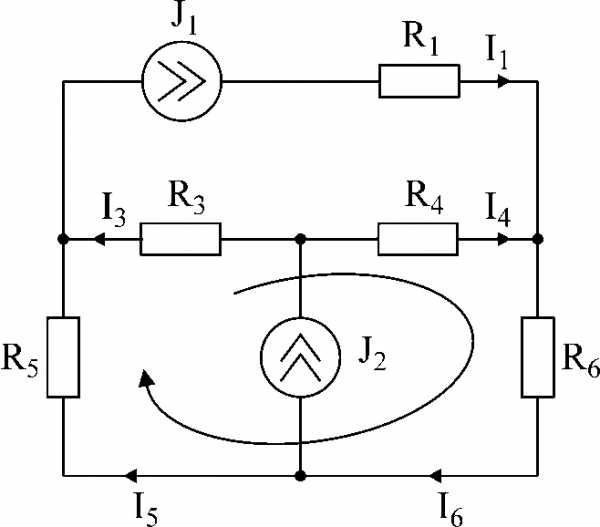
Рис.2

Решение:

Число узловых уравнений – 3, число контурных уравнений – 1.

Запомнить! При составлении уравнения по второму закону Кирхгофа выбираем контур, в который не входят источники тока. Направление контура указано на рисунке.

В данной цепи известны токи ветвей I₁ и I₂. Неизвестные токи I₃, I₄, I₅, I₆.

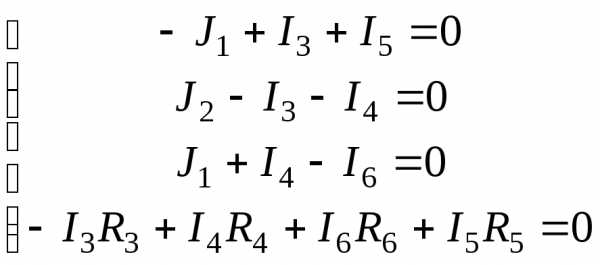
Решая систему, получаем: I₃ = 13,75 мA; I₄ = -3,75мA; I₅ = 6,25мA; I₆ = 16,25мA.

studfiles.net

Закон Ома для участка и полной замкнутой цепи

В 1826 г. немецкий ученый Георг Ом экспериментально установил прямую пропорциональную зависимость между силой тока I в проводнике и напряжением U на его концах: , где G – электрическая проводимость проводника. Величина, обратная проводимости называется электрическим сопротивле­ни­ем проводника R. Таким образом, закон Ома для участка цепи, не содержа­щего источника э.д.с., имеет вид . Учитывая, что в общем случае участок цепи может содержать и э.д.с., закон Ома следует представить в виде . Сопротивление проводника зависит от его размеров, формы и материала, из которого он изготовлен. Для однородного линейного проводника , где l – длина, S – площадь поперечного сечения проводника, r – удельное электриче­с­кое сопротивление, зависящее от материала, из которого изготовлен проводник. Единица сопротивления 1 Ом – это сопротивление такого проводника, в котором при напряжении 1В течет ток в 1А. Если цепь замкнута, то , , где R – общее сопротивление всей цепи, включая сопротивление источника э.д.с. Тогда закон Ома для замкнутой цепи следует записать , где e – алгебраическая сумма всех э.д.с., имеющихся в этой цепи. Принято называть сопротивление источника тока r – внутренним, а сопротив­ление всей остальной цепи R – внешним. Окончательный вид формулы закона Ома для замкнутой цепи . В системе единиц СИ напряжение и э.д.с. изме­ряются в Вольтах (В), сопротив­ление – в Омах (Ом), удельное электрическое сопротивление – в Ом-метрах (Ом×м), электрическая проводимость в Сименсах (См).   Рис.2.1. Отрезок проводни­ка. Закон Ома можно записать и для плотности тока. Рассмотрим участок электрической длиной dl и поперечным сечением dS (рис.2.1). Сила тока на этом участке , сопротивление , падение на­пряжения , где Е – напряженность электрического поля в проводнике. Под­ставив эти параметры в закон Ома для участка цепи, получим . Отсюда или , где – удельная электрическая проводи­мость проводникаили удельная электропроводность. В векторном виде имеем (единицей измерения g в системе СИ является сименс на метр (См/м)). Полученное выражение есть закон Ома в дифференциальной форме : плот­ность тока в любой точке внутри проводника прямо пропорциональна напря­женности поля в этой точке. 1.14 Сопротивление проводника. Явление сверхпроводимости. Способность вещества проводить ток характеризуется его удельной проводи­мостьюg, либо удельным сопротивлением r. Их величина определяется химичес­кой природой проводника и условиями, в частности температурой, при которой он находится. Для большинства металлов r растет с температурой приблизительно по линейному закону: , – удельное сопротивление при 0°С, t – температура по шкале Цельсия, a – темпе­ра­турный коэффициент сопротивления близкий к 1/273 К-1 при не очень низких темпе­ратурах. Так как R~r, то , где – сопротивление при 0°С. Преобра­зовав две последние формулы, можно записать и , где Т – температура по Кельвину. На основе температурной зависимости сопротивления метал­лов созда­ны термометры сопротивления – термисторы, позволяющие определять температуру с точно­стью до 0.003 К. При низких температурах нарушается линейность зависимости сопротивления металлов от температуры и при температуре 0 К наблюдается остаточное сопротивление Rост. Величина Rост зави­сит от чистоты материала и наличия в нем механических напряжений. Лишь у иде­ально чистого металла с идеально правильной кристаллической решеткой Rост ®0 при Т®0 (пунктирная часть кривой). Кроме этого, в 1911 г. Г.Каммерлинг-Оннес обнару­жил, что при Тк = 4.1К сопротивление ртути скачкообразно уменьшается практически до нуля. Эта температура была названа критической, а наблюдаемое яв­ление – сверхпроводимостью. Впо­следствии этот эффект был обнаружен у целого ряда дру­гих металлов (Ti, Al, Pb, Zn, V и др.) и их спла­вов в интервале температур 0.14-20 К. Вещества в сверхпроводящем состоянии обладают необычными свойствами. Однажды возбужденный в них ток может длительно существовать без источника тока. Переход в сверхпроводящее состояние сопровождается скачкообразным изме­нением теплоемкости, теплопроводности, маг­нитных свойств вещества. Выясни­лось, что внешнее магнитное поле не проникает в толщи­ну сверхпроводника, т.е. магнитная индукция внутри него всегда равна нулю. Явление сверхпроводимости объясняется на основе квантовой теории. К настоящему времени это явление обнаружено также у ряда композиционных веществ (например, соединений металлов и диэлектриков), при этом критическая температура доходит до температуры сжижения азота, что позволяет достаточно экономично использовать явление высокотемпературной сверхпроводимости в инженерной практике. Данное явление позволяет создавать: системы передачи без потерь электрического тока по проводам из таких веществ, системы для накопления электроэнергии, мощные электромагниты, магнитные подвески для различных целей. 1.15 Работа и мощность тока, закон Джоуля-Ленца. Определим работу, совершаемую постоянным током в проводнике, имеющем сопротивление R и находящемся под напряжением . Так как ток пред­ставляет собой перемещение заряда q под действием поля, то работу тока можно оп­ределить по формуле . Учитывая формулу и закон Ома, получим , или , или , где t – время протекания тока. Поделив обе части равенства на t, получим выраже­ния для мощности постоянного тока N , , . Работа тока в системе единиц СИ измеряется в доулях (Дж), а мощность – в ваттах (Вт). На практике применяются также внесистемные единицы работы тока: ватт-час (Вт×ч) и киловатт-час (кВт×ч). 1Вт×ч – работа тока мощностью 1Вт в течение одного часа. 1Вт×ч=3.6×103 Дж. Опыт показывает, что ток всегда вызывает некоторое нагревание проводника. Нагревание обусловлено тем, что кинетическая энергия движущихся по проводнику электронов (т.е. энергия тока) при каждом их столкновении с ионами металличе­ской решетки переходит в теплоту Q. Если ток идет по неподвижному металличе­скому проводнику, то вся работа тока расходуется на его нагревание и, следуя за­кону сох­ранения энергии, можно записать . Данные соотношения выражают закон Джоуля-Ленца. Впервые этот закон был установлен опытным путем Д.Джоулем в 1843 г. и независимо от него Э.Ленцем в 1844 г. Применение теплового действия тока в технике началось с открытия в 1873 г. русским инженером А.Ладыгиным лампы накаливания. На тепловом действии тока основан целый ряд электрических приборов и ус­та­новок: тепловые электроизмерительные приборы, электропечи, электросварочная аппаратура, бытовые электронагревательные приборы – чайники, кипятильники, утюги. В пищевой промышленности широко применяется метод электроконтактного нагрева, заключающийся в том, что электрический ток, проходя через продукт, об­ла­дающий определенным сопротивлением, вызывает его равномерное нагревание. На­пример, для производства колбасных изделий через дозатор фарш поступает в формы, торцевые стенки которых служат электродами. При такой обработке обес­пе­чивается равномерность нагрева по всему объему продукта, возможность под­держа­ния определенного температурного режима, наивысшая биологическая цен­ность из­делия, наименьшие длительность процесса и расход энергии. Определим удельную тепловую мощность токаw, т.е. количество теплоты, вы­деляющееся в единице объема за единицу времени. Выделим в проводнике элемен­тарный цилиндрический объем dV с поперечным сечением dS и длиной dl параллель­ной направлению тока, и сопротивлением , . По закону Джоуля-Ленца, за время dt в этом объеме выделится теплота . Тогда и, используя закон Ома для плотности тока и соотно­шение , получим . Эти соотношения выражают закон Джоуля-Ленца в дифференциальной форме.   1.16. Правило Кирхгофа для разветвленных электрических цепей. До сих пор нами рассматривались простейшие электрические цепи, состоя­щие из одного замкнутого неразветвленного контура. На всех его участках силы тока оди­наковы. Расчет I, R, e в такой цепи выполняется с помощью законов Ома. Рис.2.2.Разветвленная электрическая цепь. Более сложной является разветвленная электри­ческая цепь, состоящая из нескольких замкнутых кон­ту­ров, имеющих общие участки. В каждом контуре мо­жет быть несколько источников тока. Силы тока на от­дельных участках замкнутого контура могут быть раз­личными по величине и направлению (рис.2.2). В 1847 г. Г.Кирхгоф сформулировал два правила, значительно упрощающих расчет разветвленных цепей. Первое правило Кирхгофа: алгебраическая сумма сил токов в узле равна нулю: . Узел – точка цепи, в которой сходятся не менее трех про­водников. В электрической цепи на рис.2.2 имеются два узла А и В. Ток, входящий в узел, считается положительным, выходящий – отрицательным. Например, для узла А первое правило Кирх­гофа следует записать . Первое правило выражает закон сохранения электрического заряда, так как ни в одной точке цепи они не могут возникать или исчезать. Второе правило Кирхгофа относится к любому замкнутому контуру, выде­ленному в разветвленной цепи: алгебраическая сумма произведений токов на со­противления, включая и внутренние, на всех участках замкнутого контура равна алгебраической сумме электродвижущих сил, встречающихся в этом контуре . Контур ‑ это замкнутый участок схемы, по которому можно пройти и вернуться в исходную точку. Второе правило Кирхгофа получается из закона Ома, записанного для всех участков от узла до узла (ветвей) разветвленной схемы. В электрической цепи на рис.2.2 имеются три контура: AMNBA, CABDC, CMNDC. При этом, токи Ii в ветвях контура, совпадающие с произвольно вы­бран­ным направлением обхода контура, считаются положительными, а направлен­ные на­встречу обхода – отрицательными. Э.д.с., проходимые от «+» к «-» считаются поло­жительными и наоборот. В рассматриваемой элек­трической цепи (рис.2.2) выберем обход контуров по часовой стрелке и запишем для них уравнения по II правилу Кирхгофа: для AMNBА ; для CABDС ; для CMNDС . В данном примере внутренними сопротивлениями источников тока пренебрегаем. Первое и второе правила Кирхгофа по­зволяют составить систему линейных алгебраичес­ких уравнений, которые связывают пара­метры (I, R, ) и позволяют, зная одни, найти другие. Простые электрические цепи имеют очень большое практическое применение. В повседневной жизни полезно знать, как под­ключить динамики или проигрыватель к сте­реосистеме, как подсоединить сигнализацию для охраны или автомобильный кас­сетный проигрыватель, как зарядить аккумуляторы или осветить новогоднюю елку. Большинство электрических цепей содержит комбинацию последовательно или параллельно подключенных резисторов (резистор – это элемент цепи, обла­дающий только сопротивлением). Полное сопротивление участка цепи оп­ределяется отношением падения на­пряжения на нем к величине силы тока . При последовательном соединении (рис.2.3 а) через все резисторы течет один и тот же ток. При параллельном соединении (рис.2.3 б) полный ток равен сумме токов, те­кущих в отдельных резисторах. При последовательном соединении падение на­пряже­ния на участке АВ равно , т.е. сумме падений напряжения на трех резисторах. Разделим обе части равенства на I и получим , т.е. . Таким образом, полное сопротивление участка цепи, состоящего из последо­ва­тельно соединенных резисторов, равно их алгебраической сумме . При параллельном соединении (рис..2.3 б) мы имеем . Разделим обе части равенства на U, где U – падение напряжения на участке цепи АВ, причем , и получим . Из этого равенства следует . Величина обратная полному сопротивлению параллельно соединенных резис­торов равна алгебраической сумме величин их обратных сопротивлений . В электрическую цепь может быть включено регулируемое (изменяющееся с помощью специального движка), сопротивление, которое называется реостатом. По назначению реостаты делятся на пусковые, служащие для ограничения силы тока во время пуска двигателей, и регулирующие – для регулировки силы тока в цепи (по­степенное снижение освещенности в театральных залах), регулировки скорости вращения электродвигателей и т.д. Реостат может быть использован в качестве так называемого датчика пере­мещения. В автоматических регуляторах уровня жидкос­ти в резервуарах применя­ется поплавково-реостатный датчик. Специальный поплавок крепится к движку реостата. Изменение уровня жидкости сдвигает поплавок, изменя­ет сопротивление реостата, и следовательно, силы тока в цепи, величина которого дает информацию об уровне.   Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

zdamsam.ru

---