3 правила ньютона – Напишите мне пожалуйста 3 закона Ньютона и все формулы придлежащие к этимхзаконам
- Комментариев к записи 3 правила ньютона – Напишите мне пожалуйста 3 закона Ньютона и все формулы придлежащие к этимхзаконам нет
- Советы абитуриенту
- Напишите мне пожалуйста 3 закона Ньютона и все формулы придлежащие к этимхзаконам
- Третий закон Ньютона
- Третий закон Ньютона Википедия
- Третий закон Ньютона | Физика
- Закона ньютона 3 Закона ньютона
- 3 закона ньютона
- 3 Закона ньютона
- Ньютон – величайший ученый не только своего времени, но и истории. Он изучал природу света, построил зеркальный телескоп, но самая главная заслуга Ньютона в том, что он вывел три закона механики, которые управляют движением тел во Вселенной.
- Итак, сегодня наш урок посвящен “Законам Ньютона”.
- Давайте вспомним, о чем говорят эти законы.
- Первый Закон ньютона
- Первый Закон ньютона
- Системы отсчета, в которых выполняется первый закон Ньютона, называют инерциальными.
- Инерциальными системами отсчета называются такие системы, в которых свободные (т.е. не участвующие во взаимодействиях с другими телами) тела движутся без ускорения (т.е. равномерно и прямолинейно) или покоятся (состояние покоя, вообще говоря, следует рассматривать как частный случай равномерного движения с нулевой скоростью).
- Системы отсчета, в которых первый закон Ньютона не выполняется, называют неинерциальными.
- Первый Закон ньютона
- Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы или векторная сумма всех действующих сил (то есть равнодействующая) равна нулю.
- Чтобы изменить скорость движения, на тело необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью.
- Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела.
- Первый Закон ньютона
- Современная формулировка
- В современной физике первый закон Ньютона принято формулировать в следующем виде:
- Существуют такие системы отсчёта, называемые инерциальными, относительно которых свободная материальная точка сохраняет величину и направление своей скорости неограниченно долго.
- Второй закон Ньютона
- Второй закон Ньютона
- Современная формулировка
- В инерциальной системе отсчета ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.
- Второй закон Ньютона утверждает, что ускорение, которое получает тело, прямо пропорционально приложенной к телу силе и обратно пропорционально массе тела
- При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:
- a⃗ =F⃗ m,
- где a⃗ — ускорение материальной точки;
- F⃗ — сила, приложенная к материальной точке;
- m — масса материальной точки.
- Или в более известном виде:
- F⃗ =ma⃗ .
- Второй закон Ньютона
- В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс:
- В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил.
- dp⃗/dt=F⃗ ,
- где p⃗ — импульс точки,
- p⃗ =mv⃗ ,
- где v⃗ — скорость точки;
- t — время;
- Третий закон Ньютона
- Третий закон Ньютона
- Третий закон Ньютона
- Этот закон объясняет, что происходит с двумя взаимодействующими телами.
- Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой F⃗ 1→2, а второе — на первое с силой F⃗ 2→1. Как соотносятся силы?
- Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются
- Третий закон Ньютона
- Современная формулировка
- Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
- F⃗ 2→1=−F⃗ 1→2.
- Особенности законов Ньютона.
- Составление обобщающей таблицы
- Исторический очерк
- Основные законы механики Ньютон сформулировал в своей книге «Математические начала натуральной философии» в следующем виде.
- 1.Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние. 2.Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует. 3.Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны.
- Законы ньютона 1 2 3 кратко определение
Напишите мне пожалуйста 3 закона Ньютона и все формулы придлежащие к этимхзаконам
http://24-school.3dn.ru/publ/7-1-0-8Формулировка законов Ньютона
Первый закон Ньютона
* Первый закон Ньютона гласит: существуют системы отсчёта (называемые инерциальными) , в которых замкнутая система продолжает оставаться в состоянии покоя или прямолинейного равномерного движения. По сути, этот закон постулирует инертность тел. Это может казаться очевидным сейчас, но это не было очевидно на заре исследований природы. Так, например, Аристотель утверждал, что причиной всякого движения является сила, т. е. у него не было движения по инерции.
Инерциальная система отсчёта – это система отсчёта, связанная со свободным невращающимся телом. Свободное тело — тело, не взаимодействующее с другими телами.
Второй закон Ньютона
Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к телу силой и ускорением этого тела. Один из трех законов Ньютона.
Второй закон Ньютона утверждает, что ускорение, которое получает тело, прямо пропорционально приложенной к телу силе и обратно пропорционально массе тела.
Этот закон записывается в виде формулы:
\vec a = \vec {F} / m
где \vec a — ускорение тела, \vec {F} — сила, приложенная к телу, а m — масса тела.
Или, в более известном виде:
\vec {F} = m\vec a
Если на тело действуют несколько сил, то во втором законе Ньютона под \vec {F} подразумевается равнодействующая всех сил.
В случае, если масса тела меняется со временем, то второй закон Ньютона записывается в более общем виде:
\frac{d(m\vec \upsilon)}{dt} = \vec {F}
где m\vec \upsilon — импульс (количество движения) тела, t — время, а \frac{d}{dt} — производная по времени. Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. →
В данном законе как частный случай заключен первый закон Ньютона. Это можно видеть если \vec {F} = 0 (т. е. если на тело не действуют силы или равнодействующая сил равна нулю) при этом соответственно получаем что и \vec a = 0, а значит, тело сохраняет состояние покоя или равномерного прямолинейного движения.
Третий закон Ньютона
* Третий закон Ньютона объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой F12, а второе — на первое с силой F21. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия, F21 = −F12. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
Сам закон: Тела действуют друг на друга с силами, направленными вдоль одной и той же прямой, равными по модулю и противоположными по направлению.
Выводы
Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, надо потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел U(|r1-r2|). Тогда возникает закон сохранения суммарной механической энергии взаимодействующих тел:
{m {v}_1^2 \over 2} + {m {v}_2^2 \over 2} + U(|{r}_1 – {r}_2|) = const.
Законы Ньютона являются основными законами механики. Из них могут быть выведены все остальные законы механики.
otvet.mail.ru
Третий закон Ньютона
Силы взаимодействия тел
Замечание 1
Известно, что не бывает одностороннего действия одного тела на другое, тела всегда взаимодействуют друг с другом. Например, во время забивания гвоздя не только молоток действует на гвоздь, но и гвоздь, в свою очередь, действует на молоток, в результате чего молоток останавливается.
Выясним, с какими силами два тела действуют друг на друга. Для этого рассмотрим такие опыты.
Рисунок 1.
На рисунке 1 изображены два сцепленных друг с другом динамометра, один из которых прикреплен к вертикальной стойке С. Если потянуть за другой динамометр, то пружины обоих приборов растянутся и будут действовать друг на друга силами упругости $\overline{F}_{1} $~и $\overline{F}_{2} $, направленными в противоположные стороны. При этом показания динамометров будут одинаковы – значит, модули сил $F_{1} $, и $F_{2} $~равны.
Если за правый динамометр потянуть сильнее, то показания обоих динамометров возрастут на одну и ту же величину, т. е. опять будут равны друг другу. Значит, и в этом случае динамометры взаимодействуют с одинаковыми по модулю силами.
Тела действуют друг на друга с равными по модулю силами и в том случае, если взаимодействие происходит на расстоянии. Опыт, доказывающий это, изображен на рисунке 2.
На нем мы видим два демонстрационных динамометра на штативе. На стержни динамометров надеты круглые столики, к которым клейкой лентой прикреплены плоские керамические магниты. Магниты отталкиваются, поскольку обращены друг к другу одноименными полюсами. До начала опыта динамометры были разведены на такое расстояние, при котором силы взаимодействия магнитов были практически равны нулю и не регистрировались динамометрами.
Когда один из динамометров стали приближать к другому, их стрелки начали отклоняться от нуля в разные стороны. Это означает, что силы, с которыми магниты действуют друг на друга, противоположны по направлению.
Рисунок 2.
При сближении магнитов показания динамометров возрастают, но в каждый момент они равны друг другу — значит, магниты отталкиваются с равными по модулю силами.
Теперь рассмотрим опыт, в котором силы взаимодействия измеряются в процессе движения взаимодействующих тел. На рисунке 3 изображен самодвижущийся игрушечный трактор, который тянет на буксире металлическую коробку с грузом. В качестве буксирного троса использованы сцепленные друг с другом трубчатые динамометры, один из которых прикреплен к трактору, а второй – к коробке. Показания динамометров одинаковы, значит, движущиеся трактор и коробка действуют друг на друга с равными по модулю силами.
Рисунок 3.
Проделанные опыты свидетельствуют о том, что \textbf{силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.}
Этот закон был открыт Ньютоном и называется третьим законом Ньютона.
Третий закон Ньютона
Математическая запись третьего закона Ньютона имеет следующий вид:
Знак минус показывает, что векторы сил направлены в разные стороны.
Любое из наблюдаемых нами движений различных тел можно объяснить с помощью законов Ньютона. Например, идущий человек движется вперед благодаря тому, что он отталкивается ногами от земли, т. е. взаимодействует с ней. Человек и земля действуют друг на друга с одинаковыми по модулю и противоположно направленными силами и получают ускорения, обратно пропорциональные их массам. Поскольку масса Земли огромна по сравнению с массой человека, то ускорение Земли практически равно нулю, т. е. она не меняет свою скорость. Человек же приходит в движение относительно Земли.
Замечание 2
Следует отметить, что силы, возникающие в результате взаимодействия тел, являются силами одной и той же природы. Например, Земля и Луна взаимодействуют друг с другом посредством сил всемирного тяготения, стальной гвоздь и магнит притягиваются благодаря действию магнитных сил.
Примеры сил взаимодействия:
- сила гравитационного притяжения двух тел;
- силы притяжения и отталкивания двух магнитов;
- силы притяжения и отталкивания двух электрически заряженных тел;
- силы притяжения нуклонов в атомной ядре;
- силы, возникающие при упругой деформации;
- силы взаимодействия молекул.
Замечание 3
Следует помнить, что силы, о которых говорится в третьем законе Ньютона, никогда не уравновешивают друг друга, поскольку они приложены к разным телам. Две равные по модулю и противоположно направленные силы уравновешивают друг друга в том случае, если они приложены к одному телу. Тогда их равнодействующая равна нулю, и тело при этом находится в равновесии, т. е. либо покоится, либо движется равномерно и прямолинейно.
Пример 1
\item Две девочки катаются на скейтах, причем вторая девочка катается вместе со своим братом. Оттолкнувшись друг от друга, девочки приобрели противоположно направленные ускорения, равные
$a_{1} =2$м/с2 и $a_{2} =1,5$м/с2 соответственно. Зная массу обеих девочек $m_{1} =45$кг и $m_{2} =32$кг, вычислите массу брата.
Дано:
$m_{1} =45$кг, $m_{2} =32$кг, $a_{1} =2 \ м/c^2$, $a_{2} =1,5 \ м/c^2.$
Найти: $m$-?
Решение: Девочки, оттолкнувшись, приобрели ускорения, которые направлены по одной прямой в противоположные стороны и подействовали друг на друга с силами, которые имеют одинаковые модули и противоположные направления:
\[\overline{F}_{1} =-\overline{F}_{2} \]Запишем второй закон Ньютона для движущихся девочек:
$F_{1} =m_{1} a_{1} $ – сила, с которой вторая девочка вместе с братом действуют на первую девочку.
$F_{2} =(m_{2} +m)a_{2} $ – сила, с которой первая девочка действует на вторую девочку.
Подставив выражения для сил в выражение для третьего закона Ньютона, найдем массу брата:
$m=\frac{m_{1} a_{1} -m_{2} a_{2} }{a_{2} } =28$кг
Ответ: $m=28$кг.
spravochnick.ru
Третий закон Ньютона Википедия
Зако́ны Нью́то́на — три важнейших закона классической механики, которые позволяют записать уравнения движения для любой механической системы, если известны силы, действующие на составляющие её тела. Впервые в полной мере сформулированы Исааком Ньютоном в книге «Математические начала натуральной философии» (1687 год)[1][2]. В ньютоновском изложении механики, широко используемом и в настоящее время, эти законы являются аксиомами, базирующимися на обобщении экспериментальных результатов.
Первый закон Ньютона
Первый закон Ньютона постулирует существование инерциальных систем отсчета. Поэтому он также известен как закон инерции. Инерция (она же инертность) — свойство тела сохранять скорость своего движения неизменной по величине и направлению, когда не действуют никакие силы, а также свойство тела сопротивляться изменению его скорости. Чтобы изменить скорость движения тела, необходимо приложить некоторую силу, причём результат действия одной и той же силы на разные тела будет различным: тела обладают разной инерцией (инертностью), величина которой характеризуется их массой.
Современная формулировка
В современной физике первый закон Ньютона принято формулировать в следующем виде[3]:
Историческая формулировка
Ньютон сформулировал первый закон механики так:
Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние. |
С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и абсолютного времени, а это представление современная физика отвергает. С другой стороны, в произвольной (например, вращающейся) системе отсчёта закон инерции неверен, поэтому ньютоновская формулировка была заменена постулатом существования инерциальных систем отсчета.
Второй закон Ньютона
Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).
Масса материальной точки при этом полагается величиной постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами[4][5][6][7].
Современная формулировка
В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. |
При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:
a→=F→m,{\displaystyle {\vec {a}}={\frac {\vec {F}}{m}},}где a→{\displaystyle {\vec {a}}} — ускорение материальной точки;
F→{\displaystyle {\vec {F}}} — равнодействующая всех сил, приложенных к материальной точке;
m{\displaystyle m} — масса материальной точки.
Второй закон Ньютона может быть также сформулирован в эквивалентной форме с использованием понятия импульс:
В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней внешних сил. dp→dt=F→,{\displaystyle {\frac {d{\vec {p}}}{dt}}={\vec {F}},} |
где p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}} — импульс точки, v→{\displaystyle {\vec {v}}} — её скорость, а t{\displaystyle t} — время. При такой формулировке, как и при предшествующей, полагают, что масса материальной точки неизменна во времени[8][9][10].
Иногда предпринимаются попытки распространить сферу применения уравнения dp→dt=F→{\displaystyle {\frac {d{\vec {p}}}{dt}}={\vec {F}}} и на случай тел переменной массы. Однако, вместе с таким расширительным толкованием уравнения приходится существенным образом модифицировать принятые ранее определения и изменять смысл таких фундаментальных понятий, как материальная точка, импульс и сила[11][12].
Замечания
Когда на материальную точку действуют несколько сил, с учётом принципа суперпозиции, второй закон Ньютона записывается в виде:
ma→=∑i=1nFi→{\displaystyle m{\vec {a}}=\sum _{i=1}^{n}{\vec {F_{i}}}}или
dp→dt=∑i=1nFi→.{\displaystyle {\frac {d{\vec {p}}}{dt}}=\sum _{i=1}^{n}{\vec {F_{i}}}.}Второй закон Ньютона, как и вся классическая механика, справедлив только для движения тел со скоростями, много меньшими скорости света. При движении тел со скоростями, близкими к скорости света, используется релятивистское обобщение второго закона, получаемое в рамках специальной теории относительности.
Следует учитывать, что нельзя рассматривать частный случай (при F→=0{\displaystyle {\vec {F}}=0}) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.
Историческая формулировка
Исходная формулировка Ньютона:
Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует. |
Интересно, что если добавить требование инерциальности для системы отсчёта, то в такой формулировке этот закон справедлив даже в релятивистской механике.
Третий закон Ньютона
Этот закон описывает, как взаимодействуют две материальные точки. Возьмём для примера замкнутую систему, состоящую из двух материальных точек. Первая точка может действовать на вторую с некоторой силой F→1→2{\displaystyle {\vec {F}}_{1\to 2}}, а вторая — на первую с силой F→2→1{\displaystyle {\vec {F}}_{2\to 1}}. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия F→1→2{\displaystyle {\vec {F}}_{1\to 2}} равна по модулю и противоположна по направлению силе противодействия F→2→1{\displaystyle {\vec {F}}_{2\to 1}}.
Современная формулировка
Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: F→2→1=−F→1→2.{\displaystyle {\vec {F}}_{2\to 1}=-{\vec {F}}_{1\to 2}.} |
Закон утверждает, что силы возникают лишь попарно, причём любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, сила всегда есть результат взаимодействия тел. Существование сил, возникших самостоятельно, без взаимодействующих тел, невозможно[13].
Историческая формулировка
Ньютон дал следующую формулировку закона[1]:
Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны. |
Для силы Лоренца третий закон Ньютона не выполняется. Лишь переформулировав его как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость[14].
Следствия законов Ньютона
Законы Ньютона являются аксиомами классической ньютоновской механики. Из них, как следствия, выводятся уравнения движения механических систем, а также «законы сохранения», указанные ниже. Разумеется, есть и законы (например, всемирного тяготения или Гука), не вытекающие из трёх постулатов Ньютона.
Уравнения движения
Уравнение F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}} является дифференциальным уравнением: ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию (перемещение) механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости.
Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления, как инерция, колебания, волны.
Закон сохранения импульса
Закон сохранения импульса утверждает, что векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю[15].
Закон сохранения механической энергии
Если все силы консервативны, то возникает закон сохранения механической энергии взаимодействующих тел: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной[16].
Законы Ньютона и силы инерции
Использование законов Ньютона предполагает задание некой ИСО. Однако, на практике приходится иметь дело и с неинерциальными системами отсчёта. В этих случаях, помимо сил, о которых идёт речь во втором и третьем законах Ньютона, в механике вводятся в рассмотрение так называемые силы инерции.
Обычно речь идёт о силах инерции двух различных типов[13][17]. Сила первого типа (даламберова сила инерции[18]) представляет собой векторную величину, равную произведению массы материальной точки на её ускорение, взятое со знаком минус. Силы второго типа (эйлеровы силы инерции[18]) используются для получения формальной возможности записи уравнений движения тел в неинерциальных системах отсчёта в виде, совпадающем с видом второго закона Ньютона. По определению, эйлерова сила инерции равна произведению массы материальной точки на разность между значениями её ускорения в той неинерциальной системе отсчёта, для которой эта сила вводится, с одной стороны, и в какой-либо инерциальной системе отсчёта, с другой[13][17]. Определяемые таким образом силы инерции силами в истинном смысле слова не являются[19][13], их называют фиктивными[20], кажущимися[21] или псевдосилами[22].
Законы Ньютона в логике курса механики
Существуют методологически различные способы формулирования классической механики, то есть выбора её фундаментальных постулатов, на основе которых затем выводятся законы-следствия и уравнения движения. Придание законам Ньютона статуса аксиом, опирающихся на эмпирический материал, — только один из таких способов («ньютонова механика»). Этот подход принят в средней школе, а также в большинстве вузовских курсов общей физики.
Альтернативным подходом, использующимся преимущественно в курсах теоретической физики, выступает лагранжева механика. В рамках лагранжева формализма имеются одна-единственная формула (запись действия) и один-единственный постулат (тела движутся так, чтобы действие было стационарным), являющийся теоретической концепцией. Из этого можно вывести все законы Ньютона, правда, только для лагранжевых систем (в частности, для консервативных систем). Следует, однако, отметить, что все известные фундаментальные взаимодействия описываются именно лагранжевыми системами. Более того, в рамках лагранжева формализма можно легко рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет по-прежнему применима.
Исторический очерк
Практика применения машин в мануфактурной промышленности, строительство зданий, кораблестроение, использование артиллерии позволили ко времени Ньютона накопиться большому числу наблюдений над механическими процессами. Понятия инерции, силы, ускорения всё более прояснялись в течение XVII столетия. Работы Галилея, Борелли, Декарта, Гюйгенса по механике уже содержали все необходимые теоретические предпосылки для создания Ньютоном в механике логичной и последовательной системы определений и теорем
 Страница «Начал» Ньютона с аксиомами механики
Страница «Начал» Ньютона с аксиомами механикиОсновные законы механики Исаак Ньютон сформулировал в своей книге «Математические начала натуральной философии»[1]:
Оригинальный текст (лат.)
LEX I
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quantenus a viribus impressis cogitur statum illum mutare.LEX II
Mutationem motus proportionalem esse vi motrici impressae et fieri secundum lineam rectam qua vis illa imprimitur.LEX III
Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.
Русский перевод этих формулировок законов см. в предыдущих разделах.
Первый закон (закон инерции), в менее чёткой форме, опубликовал ещё Галилей, допускавший свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений)[24]. Галилей также сформулировал важнейший принцип относительности, который Ньютон не включил в свою аксиоматику, потому что для механических процессов данный принцип является следствием уравнений динамики. Кроме того, Ньютон считал пространство и время абсолютными понятиями, едиными для всей Вселенной, и явно указал на это в своих «Началах».
Ньютон также дал строгие определения таких физических понятий, как количество движения (не вполне ясно использованное у Декарта[24]) и сила. Он ввёл в физику понятие массы как меры инертности тела и, одновременно, его гравитационных свойств (ранее физики пользовались понятием вес).
В середине XVII века ещё не существовало современной техники дифференциального и интегрального исчисления. Соответствующий математический аппарат в 1680-е годы параллельно создавался самим Ньютоном (1642—1727), а также Лейбницем (1646—1716). Завершили математизацию основ механики Эйлер (1707—1783) и Лагранж (1736—1813).
Примечания
- ↑ 1 2 3 Исаак Ньютон. Математические начала натуральной философии. Перевод с латинского и примечания А. Н. Крылова / под ред. Полака Л. С.. — М.: Наука, 1989. — С. 40—41. — 690 с. — (Классики науки). — 5 000 экз. — ISBN 5-02-000747-1.
- ↑ Тарг С. М. Ньютона законы механики // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 370. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑ Инерциальная система отсчёта // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1988. — Т. 2. — С. 145. — ISBN 5-85270-034-7.
- ↑ «Дополнительной характеристикой (по сравнению с геометрическими характеристиками) материальной точки является скалярная величина m — масса материальной точки, которая, вообще говоря, может быть как постоянной, так и переменной величиной. … В классической ньютоновской механике материальная точка обычно моделируется геометрической точкой с присущей ей постоянной массой) являющейся мерой её инерции.» стр. 137 Седов Л. И., Цыпкин А. Г. Основы макроскопических теорий гравитации и электромагнетизма. М: Наука, 1989.
- ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
- ↑ Голубев Ю. Ф. Основы теоретической механики. — М.: МГУ, 2000. — С. 160. — 720 с. — ISBN 5-211-04244-1. «
- ↑ Журавлёв В. Ф. Основы теоретической механики. — М.: Физматлит, 2001. — С. 9. — 319 с. — ISBN 5-95052-041-3. «Масса [материальной точки] полагается постоянной, независящей ни от положения точки в пространстве, ни от времени».
- ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
- ↑ «В ньютоновской механике… m=const и dp/dt=ma». Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с..
- ↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 112. — ISBN 0-07-035048-5. «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».
- ↑ Зоммерфельд А. Механика = Sommerfeld A. Mechanik. Zweite, revidierte auflage, 1944. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 45-46. — 368 с. — ISBN 5-93972-051-X.
- ↑ Кильчевский Н. А. Курс теоретической механики. Том 1. — М.: Наука, 1977. 480 с.
- ↑ 1 2 3 4 Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — 320 с.
- ↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
- ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 282. — 416 с. — ISBN 5-06-003117-9.
- ↑ Савельев И. В. Глава 3. Работа и энергия // Курс общей физики. Механика. — 4-е изд. — М.: Наука, 1970. — С. 89—99. — ISBN 5-17-002963-2.
- ↑ 1 2 Тарг С. М. Сила инерции // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 494-495. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ 1 2 Ишлинский А. Ю. К вопросу об абсолютных силах и силах инерции в классической механике // Теоретическая механика. Сборник научно-методических статей. — 2000. — № 23. — С. 3-8.
- ↑ «”Силы инерции” — не силы». Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 21. — 46 с.
- ↑ Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 82. — 368 с. — ISBN 5-93972-051-X.
- ↑ Борн М. Эйнштейновская теория относительности. — М.: «Мир», 1972. — С. 81. — 368 с.
- ↑ Фейнман Р., Лейтон Р., Сэндс М. Выпуск 1. Современная наука о природе. Законы механики // Фейнмановские лекции по физике. — М.: «Мир», 1965. — С. 225.
- ↑ Кузнецов Б. Г. Основные принципы физики Ньютона // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 186-197;
- ↑ 1 2 Кузнецов Б. Г. Генезис механического объяснения физических явлений и идеи картезианской физики // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 160-161, 169-170, 177;
Литература
- Лич Дж. У. Классическая механика. М.: Иностр. литература, 1961.
- Спасский Б. И.. История физики. М., «Высшая школа», 1977.
- Том 1. Часть 1-я; Часть 2-я
- Том 2. Часть 1-я; Часть 2-я
- Кудрявцев П. С. Курс истории физики. — М.: Просвещение, 1974.
- Crowell, Benjamin (2011), Light and Matter (2011, Light and Matter), especially at Section 4.2, Newton’s First Law, Section 4.3, Newton’s Second Law, and Section 5.1, Newton’s Third Law.
- Feynman, R. P. The Feynman Lectures on Physics / R. P. Feynman, Leighton, Sands. — 2nd. — Pearson/Addison-Wesley, 2005. — Vol. Vol. 1. — ISBN 0-8053-9049-9.
- Fowles, G. R. Analytical Mechanics / G. R. Fowles, Cassiday. — 6th. — Saunders College Publishing, 1999. — ISBN 0-03-022317-2.
- Likins, Peter W. Elements of Engineering Mechanics. — McGraw-Hill Book Company, 1973. — ISBN 0-07-037852-5.
- Marion, Jerry. Classical Dynamics of Particles and Systems / Jerry Marion, Thornton. — Harcourt College Publishers, 1995. — ISBN 0-03-097302-3.
- NMJ Woodhouse. Special Relativity. — London/Berlin : Springer, 2003. — P. 6. — ISBN 1-85233-426-6.
- Newton, Isaac, “Mathematical Principles of Natural Philosophy”, 1729 English translation based on 3rd Latin edition (1726), volume 1, containing Book 1, especially at the section Axioms or Laws of Motion, starting page 19.
- Newton, Isaac, “Mathematical Principles of Natural Philosophy”, 1729 English translation based on 3rd Latin edition (1726), volume 2, containing Books 2 & 3.
- Thomson, W (Lord Kelvin), and Tait, P G, (1867), Treatise on natural philosophy, volume 1, especially at Section 242, Newton’s laws of motion.
Ссылки
wikiredia.ru
Третий закон Ньютона | Физика
В своем первом законе Ньютон описал состояние тела, не подверженного действию других тел. В этом случае тело либо сохраняет свое состояние покоя, либо движется равномерно и прямолинейно (относительно инерциальной системы отсчета).
Во втором законе Ньютона речь идет о прямо противоположной ситуации. Теперь на данное тело действуют внешние тела, причем их количество может быть произвольным. Под действием окружающих тел рассматриваемое тело начинает двигаться с ускорением, причем произведение массы данного тела на его ускорение оказывается равным действующей силе.
Сформулировав эти два закона, Ньютон обратился к анализу ситуации, когда во взаимодействии участвуют только два тела. Допустим, имеются два тела А и В, которые притягивают друг друга с некоторыми силами F и F’. Может ли одна из этих сил быть больше другой? Размышление над этой проблемой привело Ньютона к выводу, что такого быть не может: силы взаимодействия двух тел всегда равны друг другу. Каким образом Ньютон пришел к этому заключению? Вот как он рассуждал:
«Относительно притяжения дело может быть изложено вкратце следующим образом: между двумя взаимопритягивающимися телами надо вообразить помещенным какое-либо препятствие, мешающее их сближению. Если бы одно из тел А притягивалось телом В сильнее, нежели тело В притягивается телом А, то препятствие испытывало бы со стороны тела А большее давление, нежели со стороны тела В, и, следовательно, не осталось бы равновесия. Преобладающее давление вызвало бы движение системы, состоящей из этих двух тел и препятствия в сторону тела В, ив свободном пространстве эта система, двигаясь ускоренно, ушла бы в бесконечность. Такое заключение нелепо и противоречит первому закону… Отсюда следует, что оба тела давят на препятствие с равными силами, а значит, и притягиваются взаимно с таковыми же».
Опыты подтверждают вывод Ньютона. Если, например, взять две тележки и на одной из них закрепить магнит, а на другой — кусок железа, а затем соединить их с динамометрами, то мы увидим, что показания этих приборов совпадут (рис. 13). Это означает, что сила, с которой магнит притягивает к себе железо, равна по величине силе, с которой железо притягивает к себе магнит. Эти силы имеют равные числовые значения, но противоположные направления: сила притяжения к магниту направлена влево, а сила притяжения к железу — вправо.
Итак,
Силы, с которыми взаимодействуют любые два тела, всегда равны по величине и противоположны по направлению.
Это утверждение является третьим законом Ньютона. Третий закон Ньютона обосновывает введение самого термина «взаимодействие»: если одно тело действует на другое, то второе также действует на первое. Другими словами, не может быть такого, чтобы одно тело на другое действовало, а второе на первое — нет. Как писал сам Ньютон, «действию всегда есть равное и противоположное противодействие»; в частности, «если кто нажимает пальцем на камень, то и палец его также нажимается камнем. Если лошадь тащит камень, привязанный к канату, то и обратно (если можно так выразиться) она с равным усилием оттягивается к камню».
Из третьего закона Ньютона следует, что вес тела, т. е. сила, с которой тело давит на свою опору (или растягивает подвес), совпадает по величине с силой, действующей со стороны опоры на данное тело_ Сила, с которой опора давит на находящееся на ней тело, называется силой реакции опоры. Обозначив силу реакции опоры через N, мы можем записать:
P = N. (9.1)
Соответствующая ситуация изображена на рисунке 14.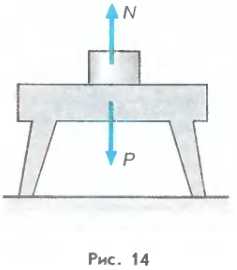
Полученная формула является более общей, чем P=mg, так как она остается справедливой и в том случае, когда тело вместе с опорой совершает ускоренное движение.
Закономерность, выражаемую формулой (9.1), можно проверить на опыте. Возьмем два демонстрационных динамометра с круглым циферблатом и поставим их друг на друга (рис. 15). Мы увидим, что верхний прибор покажет точно такую же силу, что и нижний.
Следует помнить, что силы взаимодействия, о которых говорится в третьем законе Ньютона, не могут быть приложены к одному и тому же телу: это есть силы, с которыми тела действуют друг на друга (рис. 16).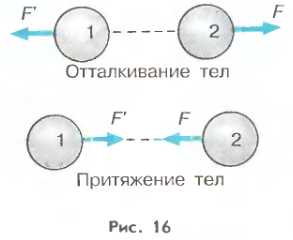
Когда Ньютона спросили, каким путем он пришел к своим открытиям, Ньютон ответил: «Всегда думал о них. Предмет исследования постоянно передо мной, и я жду, пока первые пробивающиеся лучи рассвета постепенно не осветят его сильным и ярким светом».
О том, какой титанический труд стоял на самом деле за этим «ожиданием рассвета», рассказал впоследствии его секретарь Гэмфри: «Он (Ньютон) постоянно был занят работой… Он не позволял себе никакого отдыха и передышки, не ездил верхом, не гулял, не играл в кегли, не занимался спортом; он считал потерянным всякий час, не посвященный занятиям. Редко уходил он из своей комнаты, за исключением только тех случаев, когда ему надо было читать лекции как люкасовскому профессору. Лекции мало кто посещал и еще меньше того понимал. Часто приходилось читать перед пустыми стенами… Занятиями он увлекался настолько, что часто забывал обедать. Нередко, заходя в его комнату, я находил обед нетронутым на столе, и только после моего напоминания он стоя что-нибудь съедал… Раньше двух-трех часов он редко ложился спать, а в некоторых случаях засыпал только в пять, шесть часов утра. Спал он всегда четыре или пять часов, особенно осенью и весной. Судя по его озабоченности и постоянной работе, думаю, что он стремился перейти черту человеческой силы и искусства».
Отдавая дань трудам своих великих предшественников, Ньютон говорил, что если он и «видел дальше, чем другие, то лишь потому, что стоял на плечах гигантов». А незадолго до смерти он написал: «Не знаю, каким представляет себе меня мир, но самому себе я кажусь просто ребенком, который играет на морском берегу и забавляется, отыскивая лучше обкатанные камешки или более красивые, чем обычно, ракушки, в то время как великий океан истины лежит передо мной совершенно неразгаданный».
На статуе, воздвигнутой Ньютону в Кембридже, помещена надпись: «Разумом он превосходил род человеческий». Слава Ньютона была настолько велика, что известный математик Лопиталь еще при жизни Ньютона удивлялся тому, что этот великий человек мог есть, пить и спать, как прочие люди. А в Вестминстерском аббатстве, где похоронен Ньютон, на памятнике ему можно прочитать такие слова: «Пусть смертные радуются, что существовало такое украшение рода человеческого».
Влияние взглядов Ньютона на дальнейшее развитие физики огромно. «Ньютон, — писал академик С. И. Вавилов, — заставил физику мыслить по-своему, «классически», как мы выражаемся теперь. На языке Ньютона мы думали и говорили, и только теперь делаются попытки изобрести новый язык. Вот почему можно утверждать, что на всей физике лежал индивидуальный отпечаток его мысли; без Ньютона наука развивалась бы иначе».
1. Сформулируйте третий закон Ньютона. 2. Предположим, что муха, летящая навстречу автомобилю, ударилась о его лобовое стекло. Автомобиль или муха действовали с большей силой в момент столкновения? 3. Известно, что Земля притягивает к себе все находящиеся вблизи нее тела. Притягивают ли эти тела Землю? 4. Что сильнее притягивает: яблоко Землю или Земля яблоко? 5. С какой силой численно совпадает вес тела согласно третьему закону Ньютона?
phscs.ru
3 закона ньютона3 Закона ньютона
Первый Закон ньютонаПервый Закон ньютона
Первый Закон ньютона
Первый Закон ньютона
Второй закон НьютонаВторой закон Ньютона
Второй закон Ньютона
Третий закон НьютонаТретий закон НьютонаТретий закон Ньютона
Третий закон Ньютона
Особенности законов Ньютона.Составление обобщающей таблицыИсторический очерк
1.Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.3.Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны. |
dok.opredelim.com
Законы ньютона 1 2 3 кратко определение
Математические начала натуральной философии»
Ньютон был современником Петра 1 и Людовика XIV. Окончив университет, Ньютон получил ученое звание бакалавра, затем магистра. С 1669 года стал во главе кафедры физики и математики в Кембриджском университете. Внешне жизнь Ньютона протекала спокойно, мирно и однообразно.
Но ее заполняли непрестанный труд, математические изыскания, физические и химические опыты, вызывавшие восхищение его современников.
С высокой степенью точности инерциальной системой считается система отсчета, связанная с Солнцем (гелиоцентрическая). Если рассматриваемое время движения невелико, то инерциальной можно считать систему отсчета, связанную с Землей (геоцентрическая).
Пример. В качестве примера выполнения 1 закона Ньютона можно рассмотреть движение парашютиста (см. рис. 2). Он равномерно приближается
Он утверждает, что существуют такие системы отсчета, в которых любое тело, что не подверглось воздействию внешних сил, сохраняет состояние покоя или прямолинейного равномерного движения. Закон говорит, что в этой же системе любые другие свободные тела должны вести себя абсолютно одинаково.
Состояние покоя или равномерного движения являются вполне равноправными и не требуют объяснения. Любая система, которая находится в поступательном движении, прямолинейно и равномерно по отношению к инерциальной также является инерциальной. Второй закон Ньютона говорит, что причиной изменения скорости тел, которые находятся в состоянии равномерного движения, может изменить свою скорость только при воздействии посторонних тел.
Законы ньютона 1 2 3 кратко определение
При формулировке закона инерции И. Ньютон опирался на труды Г. Галилея, который первым понял ошибочность утверждения, что тело, на которое ничто не действует, может только покоиться. Галилей показал, что такое тело может либо покоиться, либо двигаться с постоянной скоростью.
Второй закон Ньютона: под действием силы F тело массой т приобретает такое ускорение а, что произведение массы на ускорение будет равно действующей силе, т.
Второй закон Ньютона
Только пакеты берите покрепче. А теперь примерно с одинаковой силой по очереди резко поднимите оба пакета вверх.
Вы увидите, что легкий пакет практически взлетит, а вот тяжелый перемещаться будет намного медленнее. А теперь другой опыт положите на землю футбольный мячик и пните его пару раз. Один раз легонько, а второй раз со всей силы.
Понаблюдайте, как изменится скорость мяча после пинка.
Два вектора считаются равными лишь в том случае, если у них одинаковы и длины и направления (то есть они параллельны и ориентированы в одну сторону). С изменением ориентации меняется знак вектора ( на рис.1 b = а; с = — а).
Правила векторной алгебры отражают физические свойства векторных величин. Так в соответствии с тем, что равнодействующая двух сил находится по правилу параллелограмма, суммой двух векторов (a и b), определяется новый вектор (с = а + b), изображаемый диагональю параллелограмма, стороны которого – векторы-слагаемые, рис.
Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и времени, а это представление современная физика отвергает.
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка сохраняет свою скорость неизменной, если на нее не действуют другие тела.
Так завершается та «цепочка», о которой говорилось в конце третьей главы: по известным силам и массе тела находят ускорение, затем вычисляют его скорость и перемещение за любой промежуток времени и, наконец, координаты тела в любой момент времени. Для этого должны быть известны «начальные условия» — начальное положение и начальная скорость тела.
Так, например, ученым, которые руководят полетом космического корабля, необходимо, конечно, заранее знать положение корабля в любой момент времени.
Первый закон ньютона
на которое не действуют никакие тела. Так как движение и покой относительны, в различных системах отсчета движение изолированного тела будет разным.
В одной системе отсчета тело может находиться в покое или двигаться с постоянной скоростью, в другой системе это же тело может двигаться с ускорением. Существуют такие системы отсчета, относительно которых изолированные поступательно движущиеся тела сохраняют свою скорость неизменной по модулю и направлению. Свойство тел сохранять свою скорость при отсутствии действия на него других тел называется инерцией .
Взаимодействия отличаются друг от друга и количественно, и качественно. Например, ясно, что чем больше деформируется пружина, тем больше взаимодействие ее витков. Или чем ближе два одноименных заряда, тем сильнее они будут притягиваться.
В простейших случаях взаимодействия количественной характеристикой является сила. Сила — причина ускорения тел (в инерциальной системе отсчета). Сила — это векторная физическая величина, являющаяся мерой ускорения, приобретаемого телами при взаимодействии.
Если равнодействующая сила НЕ равна нулю, то тело движется равноускоренно. Собственно именно эта сила является причиной неравномерного движения. Направление равнодействующей силы всегда совпадает по направлению с вектором ускорения.
Когда требуется изобразить силы, действующие на тело, при этом тело движется равноускоренно, значит в направлении ускорения действующая сила длиннее противоположной.
Физика в конспектах
Если тело является абсолютно твердым . то точку приложения силы можно перемещать вдоль линии действия силы в пределах тела.
Импульс — векторная физическая величина, равная произведению массы тела на его скорость: p → = m v → \displaystyle>\vec> >=m\vec> >> . Энергия — характеристика движения и взаимодействия тел, их способность совершать изменения во внешнем мире.
Законы механики Ньютона
Однако Исаак Ньютон взял названные в его честь законы не из воздуха.
Они, фактически, стали кульминацией долгого исторического процесса формулирования принципов классической механики. Мыслители и математики — упомянем лишь Галилея ( см. Уравнения равноускоренного движения ) — веками пытались вывести формулы для описания законов движения материальных тел — и постоянно спотыкались о то, что лично я сам для себя называю непроговоренными условностями, а именно — обе основополагающие идеи о том, на каких принципах зиждется материальный мир, которые настолько устойчиво вошли в сознание людей, что кажутся неоспоримыми.
Третий закон Ньютона
Займемся и мы такими же изысканиями. Мы знаем, что при взаимодействии воздействуют друг на друга оба тела. Не бывает такого, чтобы одно тело толкнуло другое, а второе в ответ никак не отреагировало бы.
Такое может происходить среди по-разному воспитанных людей, но никак не в природе. Мы знаем, что если мы пинаем мяч, то мяч в ответ пинает нас. Другое дело, что мяч имеет намного меньшую массу, чем тело человека, и потому его воздействие практически не ощутимо.
Однако, если вы попробуете пнуть тяжелый железный мяч, то живо ощутите это ответное воздействие.
popularboard.ru



