Lc контур – Колебательный контур — Википедия
- Колебательный LC контур: определение, принцип действия, расчет
- 2.8. Колебательный lc – контур переменного тока
- 10 Колебательный контур: принцип работы, виды контуров, параметры и характеристики
- 2.8. Колебательный lc – контур переменного тока
- Тема занятия 5: Колебательный контур.
- LC- колебательный контур.
- Резонансный lc-контур – Большая Энциклопедия Нефти и Газа, статья, страница 1
Колебательный LC контур: определение, принцип действия, расчет
Сегодняшня нас интересует простейший колебательный контур, его принцип работы и применение.
Колебания – процесс, повторяющийся во времени, характеризуется изменением параметров системы около точки равновесия.
Первое, что приходит на ум – это механические колебания математического или пружинного маятников. Но ведь колебания бывают и электромагнитными.
По определению колебательный контур (или LC-контур) – это электрическая цепь, в которой происходят свободные электромагнитные колебания.
Такой контур представляет собой электрическую цепь, состоящую из катушки индуктивностью L и конденсатора емкостью C. Соединены эти два элемента могут быть лишь двумя способами – последовательно и параллельно. Покажем на рисунке ниже изображение и схему простейшего колебательного контура.
LC-контур
Принцип действия колебательного контура
Давайте рассмотрим пример, когда сначала мы заряжаем конденсатор и замыкаем цепь. После этого в цепи начинает течь синусоидальный электрический ток. Конденсатор разряжается через катушку. В катушке при протекании через нее тока возникает ЭДС самоиндукции, направленная в сторону, противоположную току конденсатора.
Разрядившись окончательно, конденсатор благодаря энергии ЭДС катушки, которая в этот момент будет максимальна, начнет заряжаться вновь, но только в обратной полярности.
Колебания, которые происходят в контуре – свободные затухающие колебания. То есть без дополнительной подачи энергии колебания в любом реальном колебательном контуре рано или поздно прекратятся, как и любые колеба
zaochnik.ru
2.8. Колебательный lc – контур переменного тока
Рассмотрим колебательный процесс в колебательном контуре переменного тока, который состоит из идеальной катушки L (R = 0) и конденсатора C, то есть контура без потерь (рис. 2.33). Колебательный процесс в таком контуре заключается во взаимном преобразовании электрического и магнитного полей. 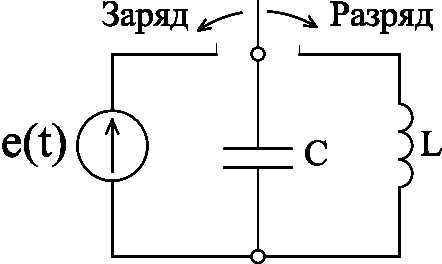
Рис.2.33. Колебательный контур
Предположим,
что конденсатор включен на заряд и
получил от источника e(t) энергию
электрического
поля 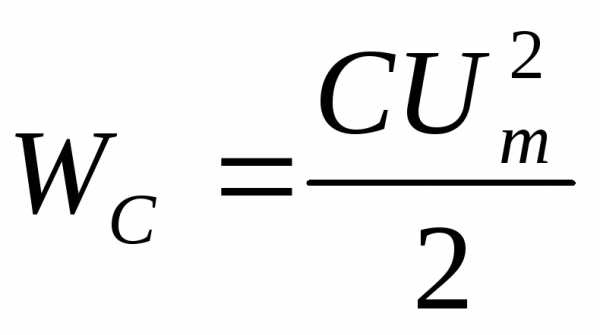 ,
после
этого конденсатор
переключен в режим разряда на катушку L.
,
после
этого конденсатор
переключен в режим разряда на катушку L.
При
этом в замкнутом контуре LC появляется ток
,
где угловая частота собственных колебаний
контура равна 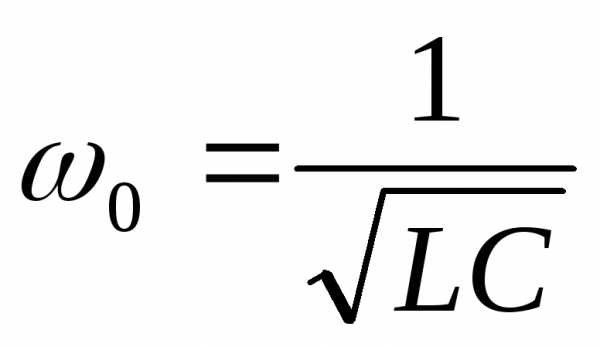
 будет переходить в энергию магнитного
поля
будет переходить в энергию магнитного
поля 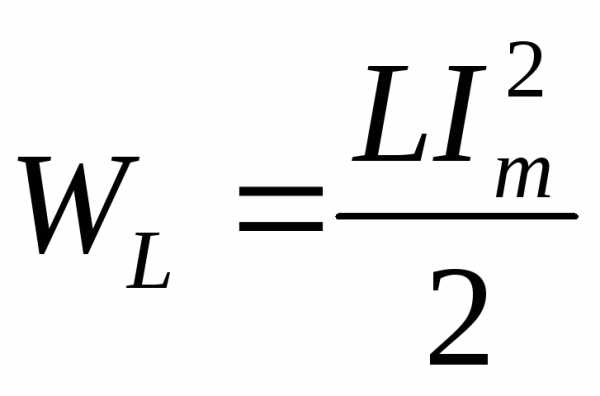 .
. На
рис. 2.34 приведены временные зависимости
мгновенных значений 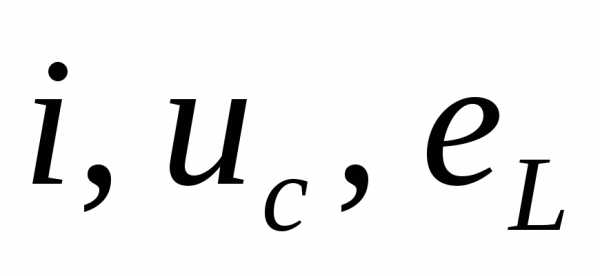 ,
а также схематически показаны процессы
разряда и заряда конденсатора C
при колебательном изменении параметров
контура.
,
а также схематически показаны процессы
разряда и заряда конденсатора C
при колебательном изменении параметров
контура.
На
практике активное сопротивление контура R ≠ 0.
В этом случае мгновенные значения
параметров 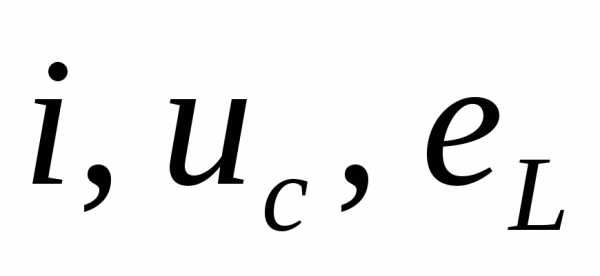 будут иметь затухающий характер. При
этом частота собственных колебаний
зависит от активного сопротивления и
определяется по формуле:
будут иметь затухающий характер. При
этом частота собственных колебаний
зависит от активного сопротивления и
определяется по формуле:
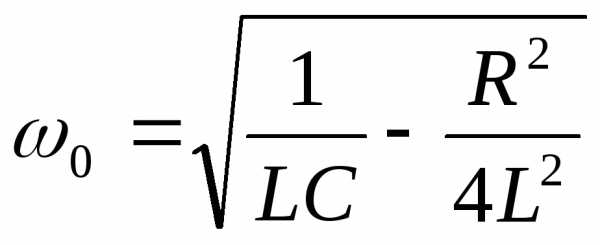 (2.35)
(2.35) 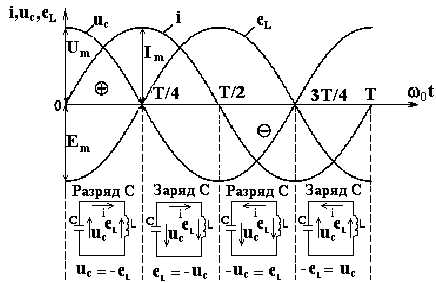
Рис.2.34.
Временные зависимости мгновенных
значений 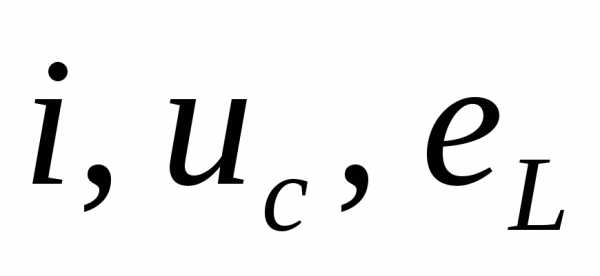 колебательного
контура
колебательного
контура
Если 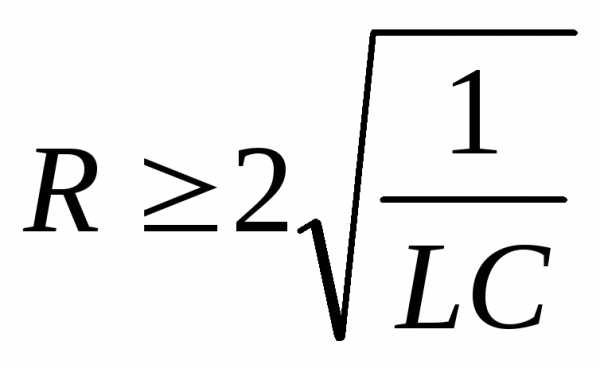 колебания в контуре не возникают. В этом
случае процессы в контуре называются
апериодическими.
колебания в контуре не возникают. В этом
случае процессы в контуре называются
апериодическими.
Лекция 5
2.9. Мощность однофазного переменного тока. Коэффициент мощности
Рис.2.35 изображает неразветвлённую цепь с активным сопротивлением R и индуктивностью L.
Рис.2.35. Цепь переменного тока с активным сопротивлением и индуктивностью
Пусть мгновенный ток в цепи изменяется по закону . Тогда мгновенное напряжение на активном сопротивлении , так как на этом участке напряжение и ток совпадают по фазе. Напряжение на катушке индуктивности , поскольку на индуктивности напряжение опережает по фазе ток на угол .
Построим для действующих значений напряжения и тока векторную диаграмму для рассматриваемой цепи (рис. 2.36).
Векторы 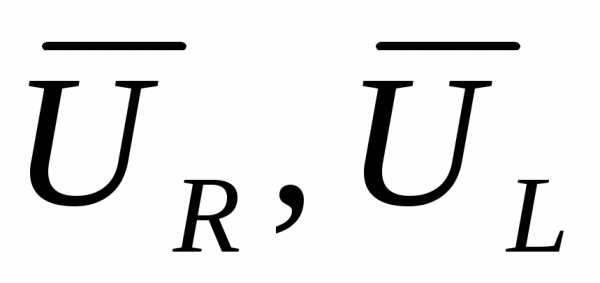 и
и  образуют треугольник напряжений. Выведем
закон Ома для этой цепи. Из треугольника
напряжений имеем
.
Но
образуют треугольник напряжений. Выведем
закон Ома для этой цепи. Из треугольника
напряжений имеем
.
Но 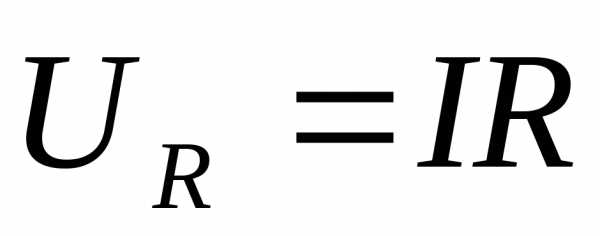 ,
а
,
где
,
а
,
где 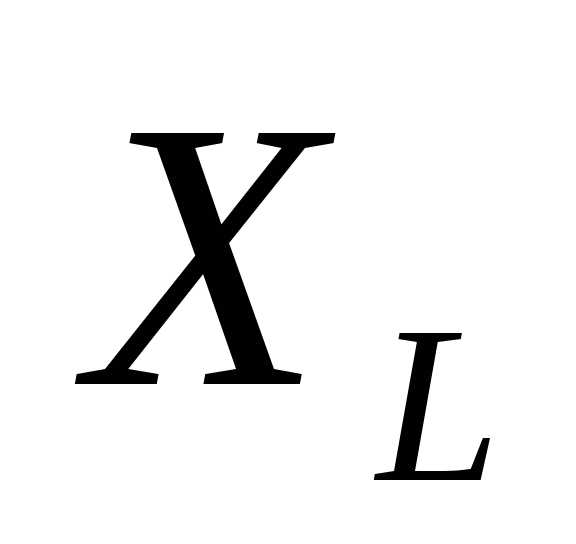 – индуктивное сопротивление, следовательно:
– индуктивное сопротивление, следовательно:
, откуда
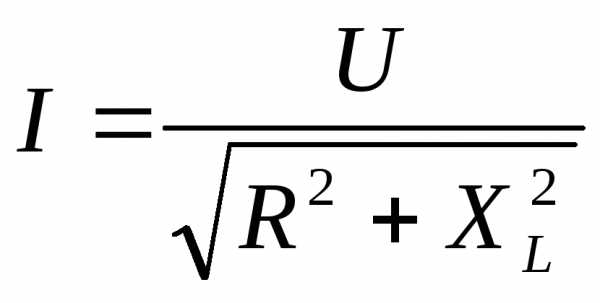
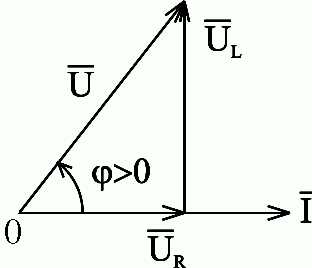
Рис.2.36. Векторная диаграмма действующих значений тока и напряжения цепи переменного тока с активным сопротивлением и индуктивностью
Введем обозначение , где Z – полное сопротивление цепи. Тогда выражение закона Ома примет вид:
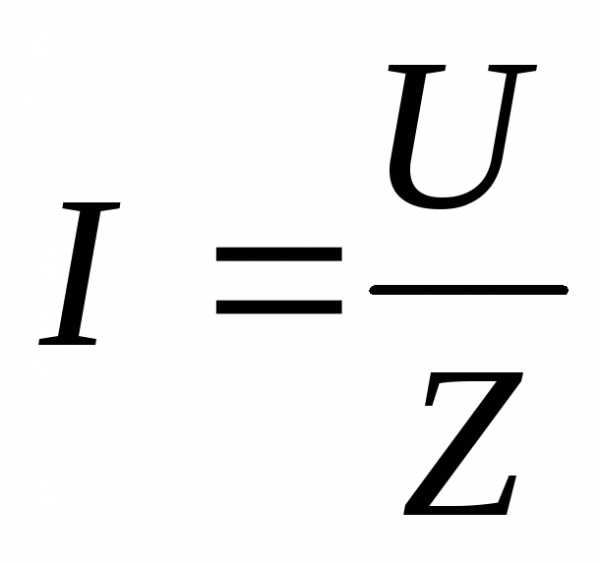 .
(2.37)
.
(2.37)
Полное сопротивление Z можно определить из треугольника сопротивлений (рис. 2.37).
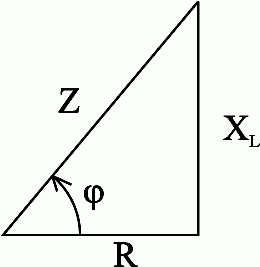
Рис.2.37. Треугольник сопротивлений цепи переменного тока с активным сопротивлением и индуктивностью
 между током и напряжением определяется
из треугольника сопротивлений:
между током и напряжением определяется
из треугольника сопротивлений: 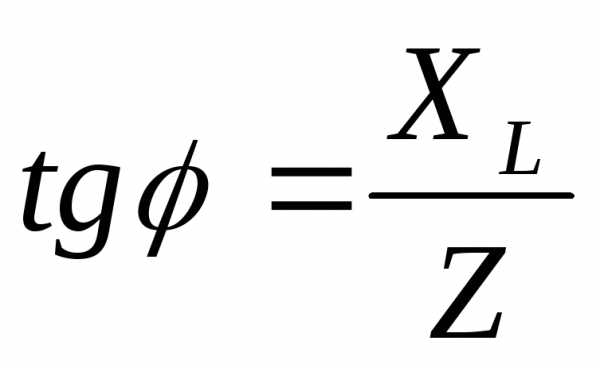 ,
(2.38)
,
(2.38)
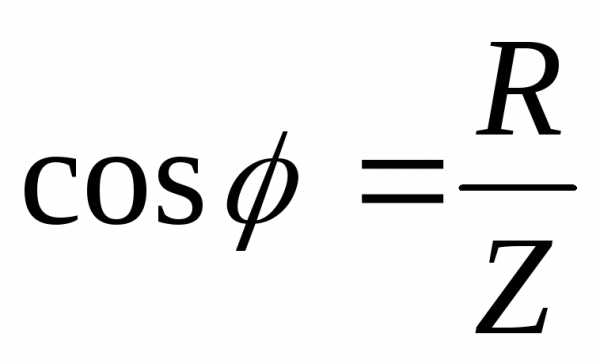 .
(2.39)
.
(2.39)
Поскольку
вектор  сдвинут по фазе относительно вектора на угол
сдвинут по фазе относительно вектора на угол  против часовой стрелки, этот угол имеет
положительное значение.
против часовой стрелки, этот угол имеет
положительное значение.
Если (рис.2.38)
,
то мгновенная мощность
.
Для действующих значений произведение 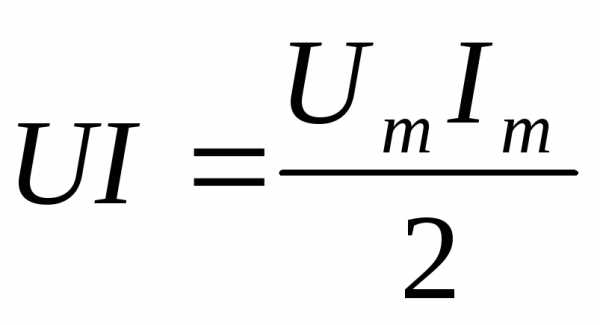 ,
откуда
.
Выражение
.
Исходя из этого,
,
откуда
.
Выражение
.
Исходя из этого,
. (2.40)
Таким
образом, мгновенная мощность переменного
тока может быть представлена в виде
постоянной величины 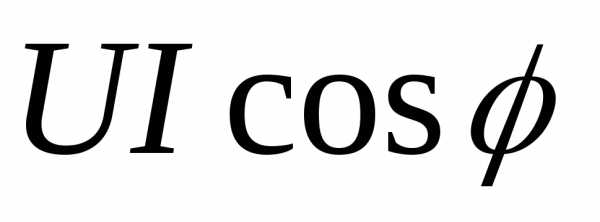 и, изменяющейся около неё с двойной
частотой, величины
.
и, изменяющейся около неё с двойной
частотой, величины
.
Введем понятие средней или активной мощности:
. (2.41)
Активная мощность характеризует расход энергии на активном сопротивлении.
Реактивная мощность характеризует обмен энергий между индуктивной катушкой и источником:
. (2.42)
Полная мощность оценивает предельную мощность нагрузки:
. (2.43)
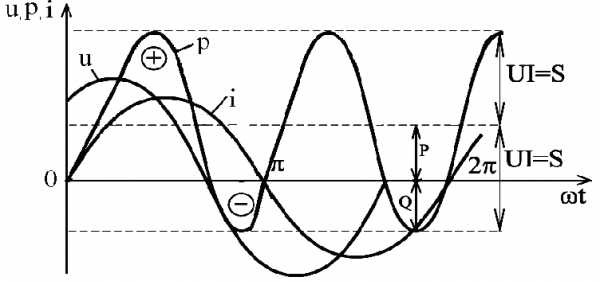
Рис.2.38. Зависимости мгновенных значений напряжения, тока и мощности цепи переменного тока с активным сопротивлением и индуктивностью
Совокупность всех мощностей можно определить из треугольника мощностей (рис. 2.39).
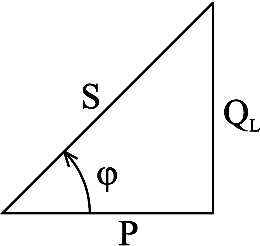
Рис.2.39. Треугольник мощностей
Так: Обозначим коэффициент мощности в виде
соотношения 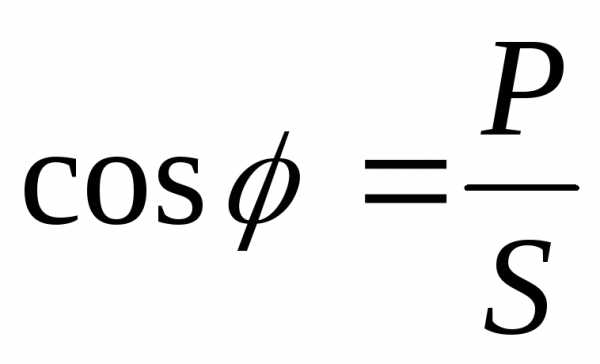 .
.
Коэффициент мощности cosφ изменяется от 0 до 1. По его величине судят, какую часть полной мощности составляет активная мощность. На практике стремятся к увеличению cosφ.
studfiles.net
10 Колебательный контур: принцип работы, виды контуров, параметры и характеристики
Колебательный контур: принцип работы, виды контуров, параметры и характеристики
Не затухающие колебания.
Принцип действия колебательного контура
Заряжаем конденсатор и замыкаем цепь. После этого в цепи начинает течь синусоидальный электрический ток. Конденсатор разряжается через катушку. В катушке при протекании через нее тока возникает ЭДС самоиндукции, направленная в сторону, противоположную току конденсатора.
Разрядившись окончательно, конденсатор благодаря энергии ЭДС катушки, которая в этот момент будет максимальна, начнет заряжаться вновь, но только в обратной полярности. Колебания, которые происходят в контуре – свободные затухающие колебания. То есть без дополнительной подачи энергии колебания в любом реальном колебательном контуре рано или поздно прекратятся, как и любые колебания в природе.
Важная характеристика LC-контура – добротность Q. Добротность определяет амплитуду резонанса и показывает, во сколько раз запасы энергии в контуре превышают потери энергии за один период колебаний. Чем выше добротность системы, тем медленнее будут затухать колебания.
Собственная частота колебательного контура
Частота свободных колебаний тока и напряжения, возникающих в колебательном контуре.
T = 2*п*(L*C)1/2. T – период электромагнитных колебаний, L и C – соответственно, индуктивность катушки колебательного контура и ёмкость элементов контура, п – число пи.
Незатухающие колебания создаются такими устройствами, которые сами могут поддерживать свои колебания за счет некоторого постоянного источника энергии. Такие устройства называются автоколебательными системами.
Любая автоколебательная система состоит из следующих четырех частей
1) колебательная система; 2) источник энергии, за счет которого компенсируются потери; 3) клапан — некоторый элемент, регулирующий поступление энергии в колебательную систему определенными порциями в нужный момент; 4) обратная связь — управление работой клапана за счет процессов в самой колебательной системе.
Генератор на транзисторе — пример автоколебательной системы. На рисунке ниже приведена упрощенная схема такого генератора, в котором роль “клапана” играет транзистор. Колебательный контур подключен к источнику тока последовательно с транзистором. Эмиттерный переход транзистора через катушку Lсв индуктивно связан с колебательным контуром. Эту катушку называют катушкой обратной связи.
При замыкании цепи через транзистор проходит импульс тока, который заряжает конденсатор С колебательного контура, в результате чего в контуре возникают свободные электромагнитные колебания малой амплитуды.
Ток, протекающий по контурной катушке L, индуцирует на концах катушки обратной связи переменное напряжение. Под действием этого напряжения электрическое поле эмиттерного перехода периодически то усиливается, то ослабляется, а транзистор то открывается, то запирается. В те промежутки времени, когда транзистор открыт, через него проходят импульсы тока. Если катушка Lсв подключена правильно (положительная обратная связь), то частота импульсов тока совпадает с частотой колебаний, возникших в контуре, и импульсы тока приходят в контур в те моменты, когда конденсатор заряжается (когда верхняя пластина конденсатора заряжена положительно). Поэтому импульсы тока, проходящие через транзистор, подзаряжают конденсатор и пополняют энергию контура, и колебания в контуре не затухают.
Если при положительной обратной связи медленно увеличивать расстояние между катушками Lсв и L, то с помощью осциллографа можно обнаружить, что амплитуда автоколебаний уменьшается, и автоколебания могут прекратиться. Это значит, что при слабой обратной связи энергия, поступающая в контур, меньше энергии, необратимо преобразуемой во внутреннюю.
Таким образом, обратная связь должна быть такой, чтобы: 1) напряжение на эмиттерном переходе изменялось синфазно с напряжением на конденсаторе контура — это фазовое условие самовозбуждения генератора; 2) обратная связь обеспечивала бы поступление в контур столько энергии, сколько ее необходимо для компенсации потерь энергии в контуре — это амплитудное условие самовозбуждения.
Частота автоколебаний равна частоте свободных колебаний в контуре и зависит от его параметров.
Уменьшая L и С, можно получить высокочастотные незатухающие колебания, используемые в радиотехнике.
Амплитуда установившихся автоколебаний, как показывает опыт, не зависит от начальных условий и определяется параметрами автоколебательной системы — напряжением источника, расстоянием между Lсв и L, сопротивлением контура.
primer-utmiit.jimdo.com
2.8. Колебательный lc – контур переменного тока
Рассмотрим колебательный процесс в колебательном контуре переменного тока, который состоит из идеальной катушки L (R = 0) и конденсатора C, то есть контура без потерь (рис. 2.33). Колебательный процесс в таком контуре заключается во взаимном преобразовании электрического и магнитного полей.
Предположим,
что конденсатор включен на заряд и
получил от источника e(t) энергию
электрического
поля 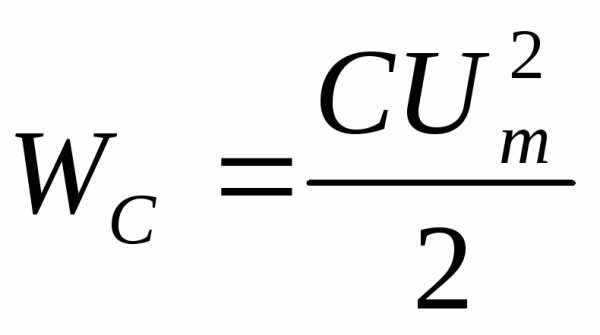 ,
после
этого конденсатор
переключен в режим разряда на катушку L.
,
после
этого конденсатор
переключен в режим разряда на катушку L.
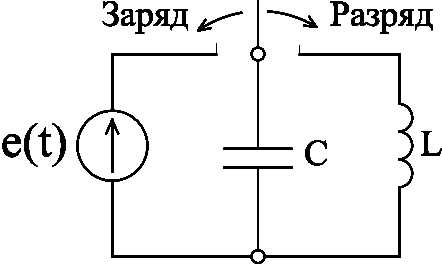
Рис.2.33. Колебательный контур
При
этом в замкнутом контуре LC появляется ток
,
где угловая частота собственных колебаний
контура равна 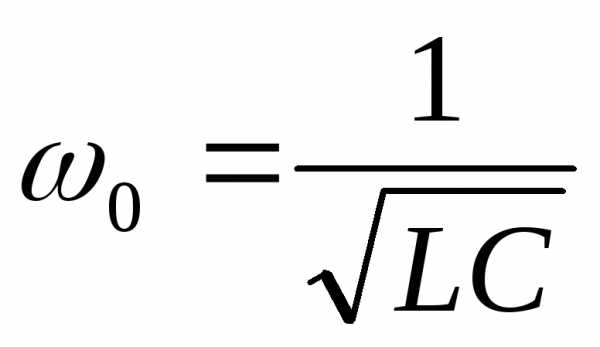 .
Конденсатор C будет разряжаться на индуктивность L,
причём
,
а на индуктивности L появится ЭДС самоиндукции eL.
При этом энергия электрического поля
.
Конденсатор C будет разряжаться на индуктивность L,
причём
,
а на индуктивности L появится ЭДС самоиндукции eL.
При этом энергия электрического поля 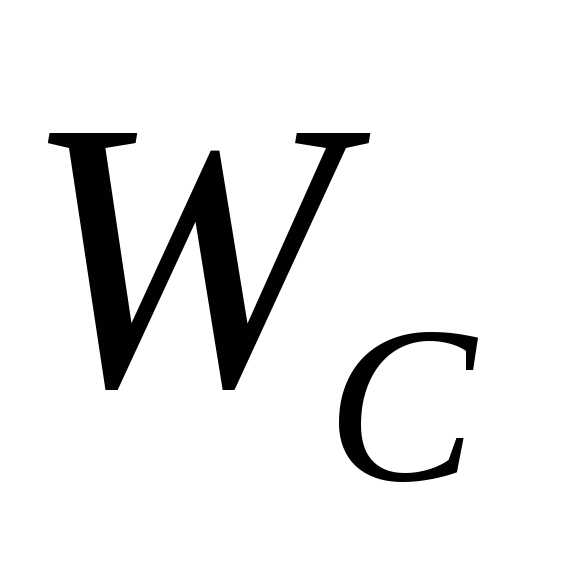 будет переходить в энергию магнитного
поля
будет переходить в энергию магнитного
поля 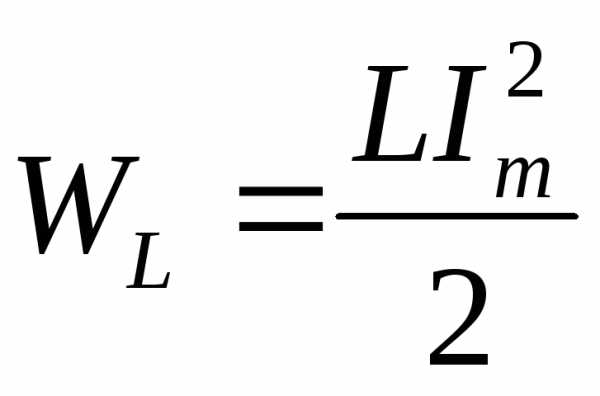 .
.
На
рис. 2.34 приведены временные зависимости
мгновенных значений 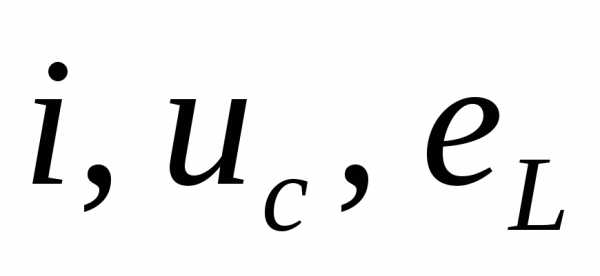 ,
а также схематически показаны процессы
разряда и заряда конденсатора C
при колебательном изменении параметров
контура.
,
а также схематически показаны процессы
разряда и заряда конденсатора C
при колебательном изменении параметров
контура.
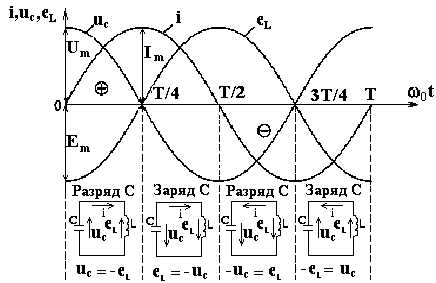
Рис.2.34.
Временные зависимости мгновенных
значений 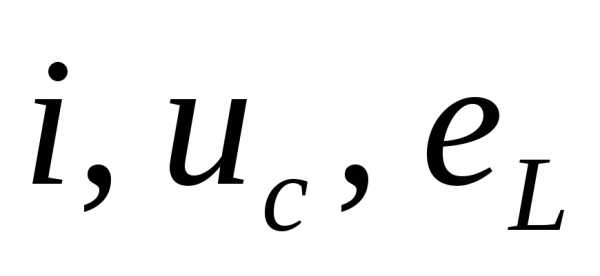 колебательного
контура
колебательного
контура
На
практике активное сопротивление контура R ≠ 0.
В этом случае мгновенные значения
параметров 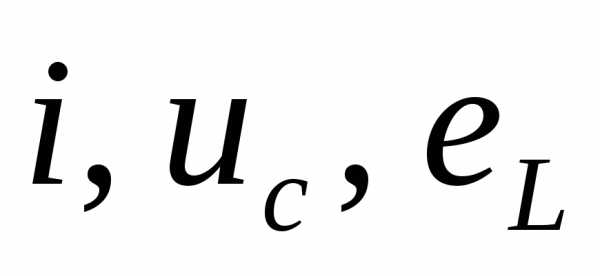 будут иметь затухающий характер. При
этом частота собственных колебаний
зависит от активного сопротивления и
определяется по формуле:
будут иметь затухающий характер. При
этом частота собственных колебаний
зависит от активного сопротивления и
определяется по формуле:
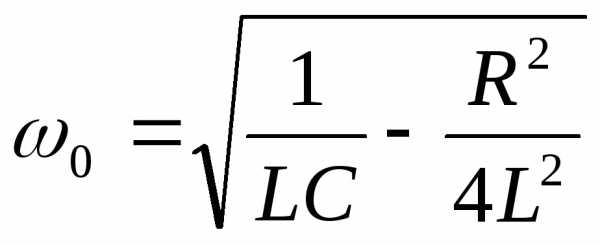 (2.35)
(2.35)
Если 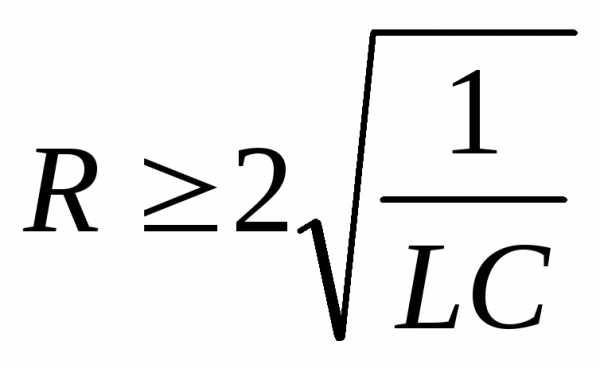 колебания в контуре не возникают. В этом
случае процессы в контуре называются
апериодическими.
колебания в контуре не возникают. В этом
случае процессы в контуре называются
апериодическими.
Лекция 5
2.9. Мощность однофазного переменного тока. Коэффициент мощности
Рис.2.35 изображает неразветвлённую цепь с активным сопротивлением R и индуктивностью L.
Рис.2.35. Цепь переменного тока с активным сопротивлением и индуктивностью
Пусть
мгновенный ток в цепи изменяется по
закону
.
Тогда мгновенное напряжение на активном
сопротивлении
,
так как на этом участке напряжение и
ток совпадают по фазе. Напряжение на
катушке индуктивности
,
поскольку на индуктивности напряжение
опережает по фазе ток на угол 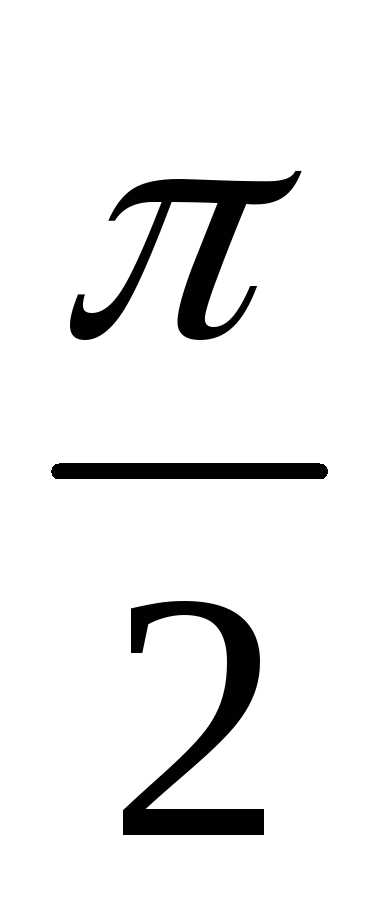 .
.
Построим для действующих значений напряжения и тока векторную диаграмму для рассматриваемой цепи (рис. 2.36).
Векторы 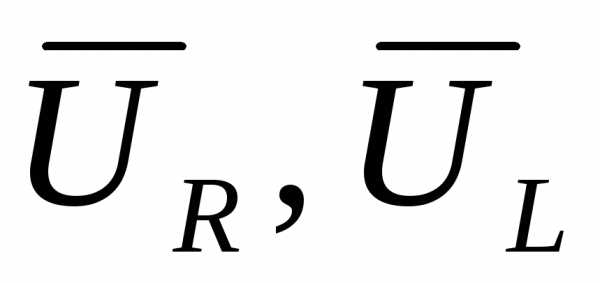 и
и  образуют треугольник напряжений. Выведем
закон Ома для этой цепи. Из треугольника
напряжений имеем
.
Но
образуют треугольник напряжений. Выведем
закон Ома для этой цепи. Из треугольника
напряжений имеем
.
Но 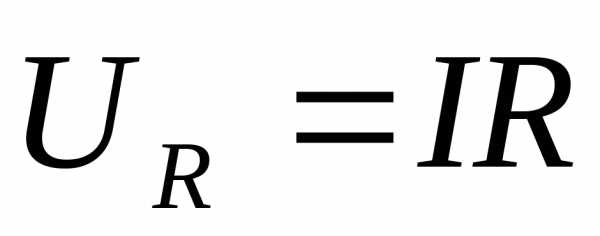 ,
а
,
где
,
а
,
где 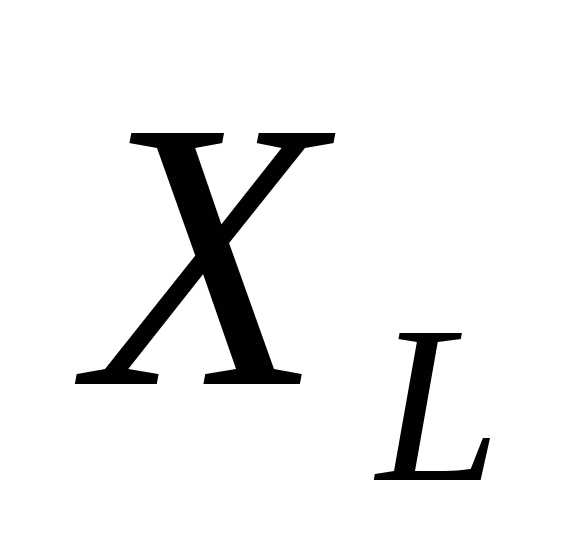 – индуктивное сопротивление, следовательно:
– индуктивное сопротивление, следовательно:
, откуда
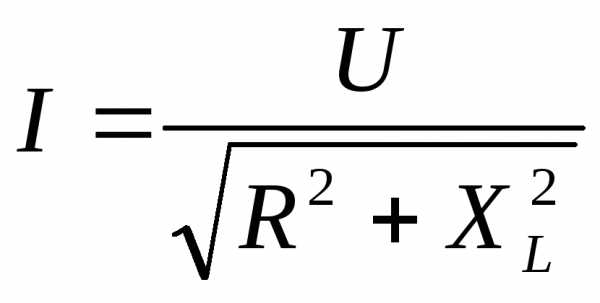 .
(2.36)
.
(2.36)
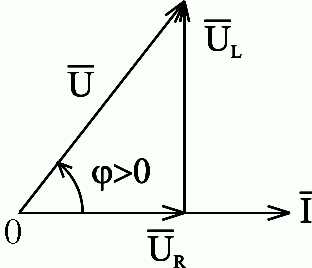
Рис.2.36. Векторная диаграмма действующих значений тока и напряжения цепи переменного тока с активным сопротивлением и индуктивностью
Введем обозначение , где Z – полное сопротивление цепи. Тогда выражение закона Ома примет вид:
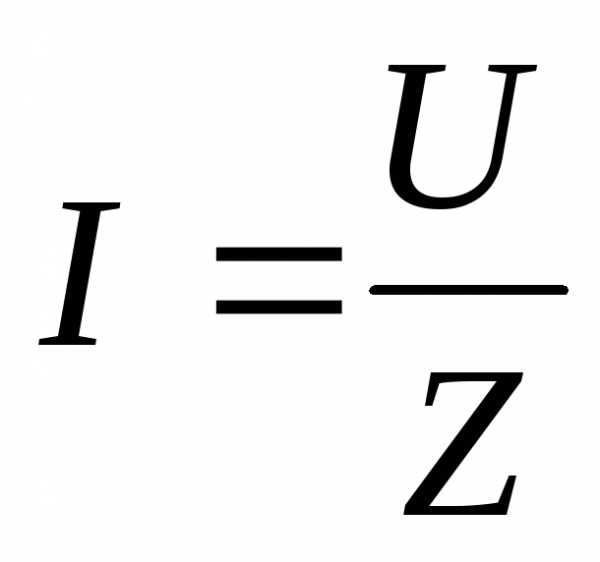 .
(2.37)
.
(2.37)
Полное сопротивление Z можно определить из треугольника сопротивлений (рис. 2.37).
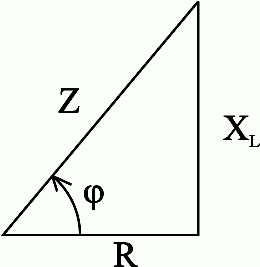
Рис.2.37. Треугольник сопротивлений цепи переменного тока с активным сопротивлением и индуктивностью
Сдвиг
фаз  между током и напряжением определяется
из треугольника сопротивлений:
между током и напряжением определяется
из треугольника сопротивлений:
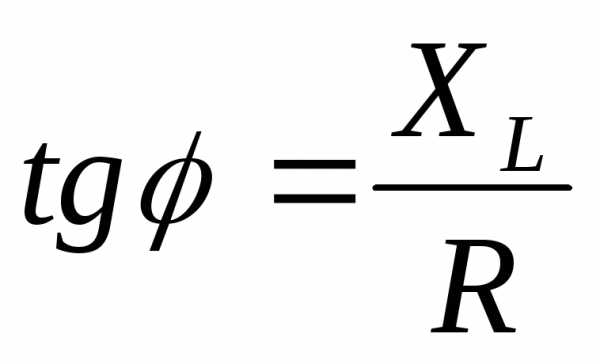 ,
(2.38)
,
(2.38)
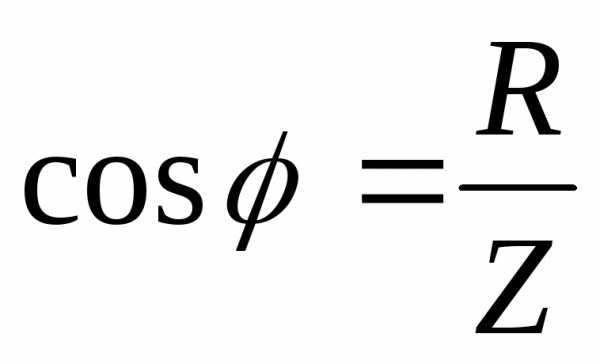 .
(2.39)
.
(2.39)
Поскольку
вектор  сдвинут по фазе относительно вектора
сдвинут по фазе относительно вектора 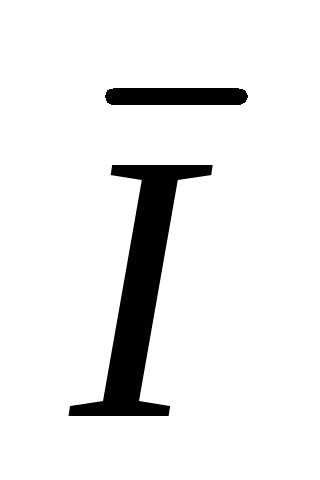 на угол
на угол  против часовой стрелки, этот угол имеет
положительное значение.
против часовой стрелки, этот угол имеет
положительное значение.
Если (рис.2.38)
,
то мгновенная мощность
.
Для действующих значений произведение 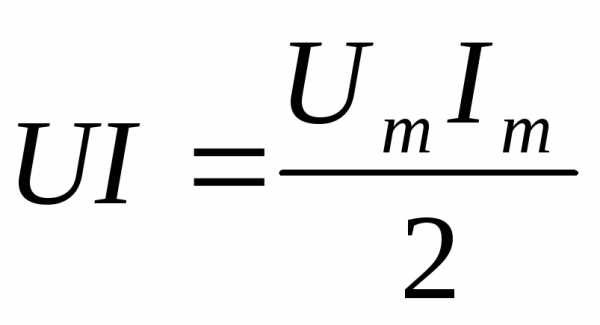 ,
откуда
.
Выражение
.
Исходя из этого,
,
откуда
.
Выражение
.
Исходя из этого,
. (2.40)
Таким
образом, мгновенная мощность переменного
тока может быть представлена в виде
постоянной величины 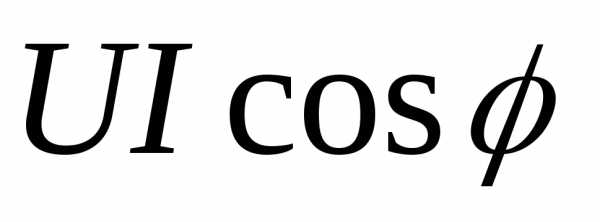 и, изменяющейся около неё с двойной
частотой, величины
.
и, изменяющейся около неё с двойной
частотой, величины
.
Введем понятие средней или активной мощности:
. (2.41)
Активная мощность характеризует расход энергии на активном сопротивлении.
Реактивная мощность характеризует обмен энергий между индуктивной катушкой и источником:
. (2.42)
Полная мощность оценивает предельную мощность нагрузки:
. (2.43)
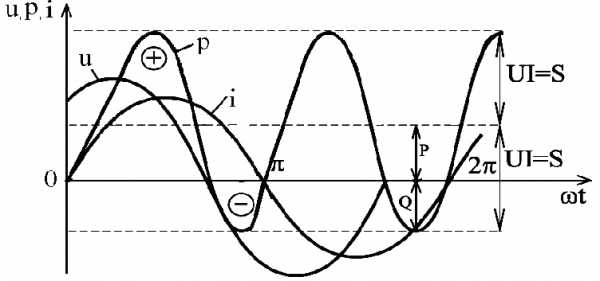
Рис.2.38. Зависимости мгновенных значений напряжения, тока и мощности цепи переменного тока с активным сопротивлением и индуктивностью
Совокупность всех мощностей можно определить из треугольника мощностей (рис. 2.39).
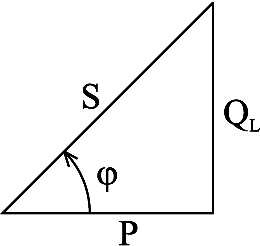
Рис.2.39. Треугольник мощностей
Так: Обозначим коэффициент мощности в виде
соотношения 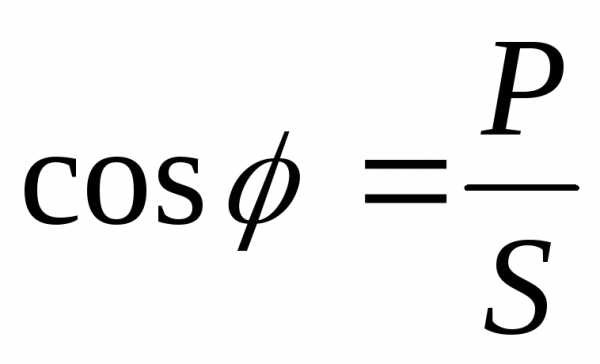 .
.
Коэффициент мощности cosφ изменяется от 0 до 1. По его величине судят, какую часть полной мощности составляет активная мощность. На практике стремятся к увеличению cosφ.
studfiles.net
Тема занятия 5: Колебательный контур.
5.1 Идеальный колебательный контур.
Колебательный контур называется идеальным, если он состоит из катушки и емкости и в нем нет сопротивления потерь.
Р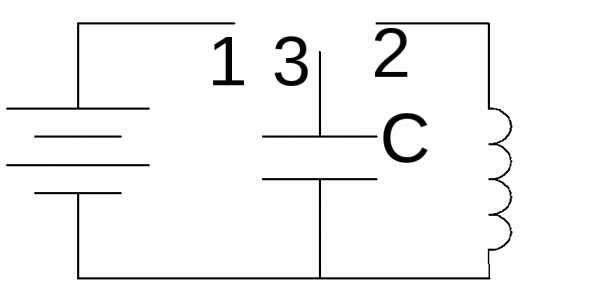 ассмотрим
физические процессы в следующей цепи:
ассмотрим
физические процессы в следующей цепи:
1 Ключ стоит в положении 1. Конденсатор начинает заряжаться, от источника напряжения и в нем накапливается энергия электрического поля,
т.е.конденсатор становится источником электрической энергии.
2. Ключ в положении 2. Конденсатор начнет разряжаться. Электрическая энергия, запасенная в конденсаторе переходит в энергию магнитного поля катушки.
Ток в цепи достигает максимального значения(точка 1). Напряжение на обкладках конденсатора уменьшается до нуля.
В период от точки 1 до точки 2 ток в контуре уменьшается до нуля, но как только он начинает уменьшатся , то уменьшается магнитное поле катушки и в катушке индуцируется ЭДС самоиндукции, который противодействует уменьшению тока, поэтому он уменьшается до нуля не скачкообразно, а плавно. Так как возникает ЭДС самоиндукции, то катушка становится источником энергии. От этой ЭДС конденсатор начинает заряжаться, но с обратной полярностью (напряжение конденсатора отрицательное) (в точке 2 конденсатор вновь заряжается).
Вывод: в цепи LC происходит непрерывное колебание энергии между электрическим и магнитным полями, поэтому такая цепь называется колебательным контуром.
Получившиеся колебания называются свободнымиилисобственными, поскольку они происходят без помощи постороннего источника электрической энергии, внесенной ранее в контур (в электрическое поле конденсатора). Так как емкость и индуктивность идеальны (нет сопротивления потерь) и энергия из цепи не уходит, амплитуда колебаний с течением времени не меняется и колебания будут незатухающими.
Определим угловую частоту свободных колебаний:
Используем равенство энергий электрического и магнитного полей
,где ώ угловая частота свободных колебаний.
[ ώ ]=1/с
f0=ώ/2π [Гц].
Период свободных колебаний Т0=1/f.
Частоту свободных колебаний называют частотой собственных колебаний контура.
Из выражения: ώ²LC=1получимώL=1/Cώ, следовательно, при токе в контуре с частотой свободных колебаний индуктивное сопротивление равно емкостному сопротивлению.
Характеристические сопротивления.
Индуктивное или емкостное сопротивление в колебательном контуре при частоте свободных колебаний называется характеристическим сопротивлением.
Характеристическое сопротивление вычисляется по формулам:
5.2 Реальный колебательный контур
Реальный колебательный контур обладает активным сопротивлением, поэтому при воздействии в контуре свободных колебаний энергия предварительно заряженного конденсатора постепенно тратится, преобразуясь в тепловую.
Свободные колебания в контуре являются затухающими, так как в каждый период энергия уменьшается и амплитуда колебаний в каждый период будет уменьшаться.
Рисунок – реальный колебательный контур.
Угловая частота свободных колебаний в реальном колебательном контуре :
Если R=2… , то угловая частота равна нулю, следовательно свободные колебания в контуре не возникнут.
Таким образом колебательным контуромназывается электрическая цепь состоящая из индуктивности и емкости и обладающая малым активным сопротивлением, меньшим удвоенного характеристического сопротивления, что обеспечивает обмен энергией между индуктивностью и емкостью.
В реальном колебательном контуре свободные колебания затухают тем быстрее, чем больше активное сопротивление.
Для характеристики интенсивности затухания свободных колебаний используется понятие «затухание контура» – отношение активного сопротивления к характеристическому.
На практике используют величину, обратную затуханию – добротность контура.
Для получения незатухающих колебаний в реальном колебательном контуре необходимо в течение каждого периода колебаний пополнять электрическую энергию на активном сопротивлении контура в такт с частотой собственных колебаний. Это осуществляется с помощью генератора.
Если подключить колебательный контур к генератору переменного тока, частота которого отличается от частоты свободных колебаний контура, то в цепи протекает ток с частотой равной частоте напряжения генератора. Эти колебания называют вынужденным.
Если частота генератора отличается от собственной частоты контура, то такой колебательный контур является ненастроенным относительно частоты внешнего воздействия, если же частоты совпадают, то настроенным.
Задача: Определить индуктивность , угловую частоту контура, характеристическое сопротивление, если емкость колебательного контура 100 пФ, частота свободных колебаний 1,59 МГц.
Решение:
Тестовые задания:
Добротность колебательного контура определяется по формуле: |
|
Какие колебания называются свободными |
|
Тема занятия 8: РЕЗОНАНС НАПРЯЖЕНИЙ
Резонанс напряжений – явление возрастания напряжений на реактивных элементах, превышающих напряжение на зажимах цепи при максимальном токе в цепи, которое совпадает по фазе с входным напряжением.
Условия возникновения резонанса:
Последовательное соединение LиCс генератором переменного тока;
Частота генератора должна быть равна частоте собственных колебаний контура , при этом характеристические сопротивления равны;
Сопротивление должно быть меньше, чем 2ρ, так как только в этом случае в цепи возникнут свободные колебания, поддерживаемые внешним источником.
Полное сопротивление цепи:
=R,
так как равны характеристические сопротивления. Следовательно, при резонансе цепь носит чисто активный характер, значит, входное напряжение, и ток в момент резонанса совпадают по фазе. Ток принимает максимальное значение.
При максимальном значении тока напряжение на участках L и C будут большими и равными между собой.
Напряжение на зажимах цепи:
.
Рассмотрим следующие соотношения:
, следовательно
.
Q –добротность контура –при резонансе напряжения показывает, во сколько раз напряжение на реактивных элементах больше входного напряжения генератора, питающего цепь. При резонансе коэффициент передачи последовательного колебательного контура
резонанса.
Пример:
Если добротность равна 100, напряжение на зажимах 1В, то
Uc=Ul=QU=100В,
то есть напряжение на зажимах меньше напряжений на емкости и индуктивности. Это явление называется резонансом напряжений
При резонансе, коэффициент передачи равен добротности.
Построим векторную диаграмму напряжения
Напряжение на емкости равно напряжению на индуктивности, следовательно напряжение на сопротивлении равно напряжению на зажимах и совпадает по фазе с током.
Рассмотрим энергетический процесс в колебательном контуре:
В цепи имеется обмен энергии между электрическим полем конденсатора и магнитным полем катушки. К генератору энергия катушки не возвращается. От генератора в цепь поступает такое количество энергии, которое тратится на резисторе. Это необходимо для того, чтобы в контуре наблюдались незатухающие колебания. Мощность в цепи только активная.
Докажем это математически:
, полная мощность цепи, которая равна активной мощности.
, реактивная мощность.
8.1 Резонансная частота. Расстройка.
В цепи, содержащей реактивные элементы, произойдет резонанс, если цепь имеет резистивный характер:
Lώ=l/ώC, следовательно
, угловая резонансная частота.
Из формулы видно, что резонанс наступает, если частота питающего генератора равна собственным колебаниям контура.
При работе с колебательным контуром необходимо знать, совпадает ли частота генератора и частота собственных колебаний контура. Если частоты совпадают, то контур остается настроенным в резонанс, если не совпадает – то в контуреприсутствует расстройка.
Настроить колебательный контур в резонанс можно тремя способами:
1 Изменять частоту генератора , при значениях емкости и индуктивности const, то есть изменяя частоту генератора мы подстраиваем эту частоту под частоту колебательного контура
2 Изменять индуктивность катушки, при частоте питания и емкости const;
3 Изменять емкость конденсатора , при частоте питания и индуктивности const.
Во втором и третьем способе изменяя частоту собственных колебаний контура, подстраиваем ее под частоту генератора.
При ненастроенном контуре частота генератора и контура не равны, то есть присутствует расстройка.
Расстройка – отклонение частоты от резонансной частоты.
Существует три вида расстройки:
Абсолютная – разность между данной частотой и резонансной
Обобщенная – отношение реактивного сопротивления к активному:
Относительная – отношение абсолютной расстройки к резонансной частоте:
При резонансе все расстройки равны нулю, если частота генератора меньше частоты контура, то расстройка считается отрицательной,
Если больше – положительной.
Таким образом добротность характеризует качество контура, а обобщенная расстройка- удаленность от резонансной частоты.
8.2 Построение зависимостейX, XL, XC отf.
Задачи:
Сопротивление контура 15 Ом, индуктивность 636 мкГн, Емкость 600 пФ, напряжение питающей сети 1,8 В. Найти собственную частоту контура, затухание контура, характеристическое сопротивление, ток, активную мощность, добротность, напряжение на зажимах контура.
Решение:
Напряжение на зажимах генератора 1 В, частота питающей сети 1 МГц, добротность 100, емкость 100 пФ. Найти: затухание, характеристическое сопротивление, активное сопротивление, индуктивность, частоту контура, ток, мощность, напряжения на емкости и индуктивности.
Решение:
Тестовые задания:
Отношение реактивного сопротивления к активному это : | А) Абсолютная расстройка; Б) Обобщенная расстройка; В) Относительная расстройка. |
Тема занятия 9 : Входные и передаточные АЧХ и ФЧХ последовательного колебательного контура.
9.1 Входные АЧХ и ФЧХ.
В последовательном колебательном контуре:
, где
R – активное сопротивление;
X – реактивное сопротивление.
Учитывая, что
,то
ώ=0 ζ=-∞ Z=∞
ώ=ώ۪۪ζ=0 Z=R
ώ=∞ ζ=∞ Z=∞, следовательно график имеет вид:
Из графика видно, что контур обладает наименьшим сопротивлением на резонансной частоте, при увеличении расстройки сопротивление увеличивается.
ζ=0 φ=0 R
ζ=1 φ=45° RL
ζ=-1 φ=-45° RC
ζ=∞ φ=90° L
ζ=-∞ φ=-90° C.
Построим график:
На участке ζ=[-1;1]
ФЧХ имеет линейный
характер.
На участке ζ=[-∞;0] – цепь носит активно-емкостной характер;
На участке ζ=[0;∞]- цепь носит frnbdyj-индуктивный характер;
При ζ=0 – цепь носит активный характер;
Передаточные АЧХ и ФЧХ
передаточная характеристика АЧХ
ζ=-∞ k=0
ζ=0 k=Q
ζ=∞ k=0
Построим график зависимости:
Разделим k∕kои получим передаточную
характеристику АЧХ в относительных
единицах, которая имеет вид:
Чтобы построить передаточную ФЧХ необходимо: построить входную ФЧХ, взять её зеркальное ее отображение и сместить на -90°.
На участке ζ=[-1;1] – передаточная ФЧХ носит линейный характер.
studfiles.net
LC- колебательный контур.
Поиск ЛекцийДля понимания работы генератора необходимо знать устройство и функционирование частотно-избирательных цепей, которые входят обязательной составной частью в состав любого генератора. В дальнейшем будем рассматривать цепи, в состав которых не входит никаких источников энергии, и которые содержат две пары зажимов: одна из которых называется входом, а другая – выходом.
Прежде всего, рассмотрим цепь, состоящую из параллельно соединённых индуктивности и ёмкости, носящей название LC- колебательный контур. При подаче на вход такой цепи набора колебаний с разными частотами на выходе будем иметь колебания, частоты которых будут лежать в достаточно узком диапазоне. Вне этого диапазона (вне этой полосы частот) указанная цепь не пропускает колебаний. Полоса пропускания LC- цепи 2 определяется на уровне , где есть коэффициент пропускания цепи при резонансной частоте . Эта частота определяется формулой Томсона:
.
Колебания на этой частоте в LC-контуре продолжались бы вечно, если бы не было потерь энергии, например, на активном сопротивлении провода катушки индуктивности. Чем меньше потери энергии, тем выше добротность контура , которая определяется как
,
и может составлять десятки и сотни. Потери в контурном конденсаторе обычно малы по сравнению с потерями в катушке, поэтому добротность контура практически равна добротности катушки. Добротность же катушки определяется как отношение реактивного сопротивления катушки к её активному сопротивлению.
2.2. RC- избирательные цепочки.
Кроме LC- контура частотно зависимыми характеристиками обладают структуры, содержащие только ёмкости и сопротивления. Эти цепи по-разному изменяют фазу сигнала . Это надо учитывать при использовании RC-цепей в качестве цепей ПОС при построении генераторов гармонических колебаний.
Рассмотрим некоторые из RC-цепей.
Рис.6.
На рис. 6 представлена схема Г-образной RC-цепи, состоящая из трёх одинаковых RC-звеньев. Каждое звено сдвигает фазу на 600. Если выполняются соотношения и , то для трёхзвенной RC-цепи = 1800 и , то есть такая цепь ослабляет выходной сигнал в 29 раз. Частоту, при которой = 180о называют квазирезонансной . Для представленного на рис. 6 вида RC-цепи . В этой цепи резисторы R включены параллельно, поэтому такая цепь называется «фазосдвигающая цепочка R-параллель». Аналогичными частотно-зависимыми свойствами обладают RC-цепи, где ёмкости и сопротивления поменялись местами. В этом случае квазирезонансная частота оказывается выше и определяется формулой . Такая фазосдвигающая цепочка называется «C-параллель».
Для реализации генератора с фазосдвигающей цепочкой достаточно использовать однокаскадный усилитель. Такой усилитель обеспечивает и должен иметь коэффициент усиления .
Другой разновидностью частотно-зависимой цепи, используемой в RC-генераторах, является мост Вина. Его схема приведена на рис. 7.
Рис.7.
При условии и квазирезонансная частота , коэффициент передачи , а фазовый угол .
Для реализации конкретных схем RC-генераторов надо учитывать величины и , которыми обладают конкретные цепи ПОС. Так, например, если по каким-либо причинам решено использовать фазосдвигающую цепочку, следует использовать усилитель, обеспечивающий сдвиг фаз усиливаемого сигнала на 1800. В этом случае усилитель должен иметь нечетное число каскадов усиления (имеются в виду схемы с общим эмиттером). Попутно упомянем о факте, что ПОС с фазосдвигающей цепочкой приводит к сильному шунтированию усилительного каскада и снижению его коэффициента усиления. В ряде случаев этого можно избежать, если между усилительным каскадом и цепью ПОС поставить эмиттерный повторитель. Такой каскад обладает большим входным сопротивлением и не вносит сдвига фаз.
Так как мост Вина не вносит фазовых сдвигов в передаваемый им сигнал ( ), то для соблюдения условия баланса фаз усилительная часть генератора должна состоять из чётного числа каскадов (на схеме с общим эмиттером).
В заключение отметим, что использование RC-цепей при создании генераторов синусоидальных колебаний позволяет изменять частоту. Однако для этого необходимо одновременно и одинаково изменять значения емкостей или сопротивлений, входящих в состав этих цепей.
Рекомендуемые страницы:
poisk-ru.ru
Резонансный lc-контур – Большая Энциклопедия Нефти и Газа, статья, страница 1
Резонансный lc-контур
Cтраница 1
Векторная диаграмма резонансного LC-контура с тем боль – ( а) и частотная характеристика шей добротностью, чем уже этот ( б) моста Вина. [1]
По существу, резонансный LC-контур выполняет функцию формирования временной диаграммы тока через ключ Sr В момент включения транзисторного ключа напряжение на нем ( КСЕили КР8) доходит до состояния насыщения, в то время, как его ток нарастает постепенно по квазисинусоидальной форме. Вследствие резонанса в цепи L C ток, протекающий через ключ 5, через некоторое время становится отрицательным и, таким образом, происходит естественная коммутация. [3]
Такая схема называется параллельным резонансным LC-контуром или избирательной схемой. Чем выше импеданс источника, тем острее пик характеристики; как вы вскоре убедитесь, в качестве источника принято использовать устройство типа источника тока. Коэффициент добротности Q позволяет оценивать характеристику контура: чем больше добротность, тем острее характеристика. [4]
Типовая схема с последовательным резонансным LC-контуром показана на рис. 10 – 7, а. Контур включен в цепь положительной обратной связи через согласующий трансформатор Трг с коэффициентом трансформации п wz / Wi. По цепи LC-контура протекает переменный ток г 0, имеющий форму, близкую к синусоидальной, поскольку обычно добротность контура достаточно высока. Переключение транзисторов и изменение полярности выходного напряжения генератора происходят в момент времени, когда транзистор вследствие снижения тока базы до уровня / 60 выходит из насыщения и входит в линейный режим. [5]
Эквивалентная схема резонатора представляет собой резонансный LC-контур, обладающий высокой добротностью. Поскольку мощность колебаний в таком контуре весьма мала, резонатор обычно включается через. [6]
В генераторах гармонических колебаний колебательными системами служат резонансные LC-контуры ( в СВЧ-генераторах для этих целей используются резонаторные системы) и частотно-зависимые ( фазирующие) ЛС-цепи. Генераторы гармонических колебаний с LC-контурами называются LC-генераторами, а с фазирующими ЛС-цепями – RC-гене-раторами. [7]
Чаще всего резонансный усилитель реализуется в виде каскадов с параллельным резонансным Lc-контуром. [8]
Элементом, включаемым параллельно нагрузке, может быть конденсатор большой емкости или последовательный резонансный LC-контур. [9]
Эта схема представляет собой генератор гармонических колебаний с индуктивной обратной связью на резонансном LC-контуре. [11]
С-генераторы ( мостовые) и генераторы с фазосдвигающей цепочкой, которые не имеют резонансных LC-контуров. [13]
Магнитные модуляторы возбуждаются от генератора прямоуголь-шх импульсов частотой 900 гц со стабилизацией ее с помощью резонансного LC-контура в цепи обратной связи генератора. [14]
В представленной схеме энергия из защитного конденсатора передается в источник питания при промежуточном накоплении в индуктивности резонансного LC-контура. [15]
Страницы: 1 2 3
www.ngpedia.ru



