Матрица обратная математика – Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.
- Комментариев к записи Матрица обратная математика – Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы. нет
- Советы абитуриенту
Обратная матрица. Примеры вычисления
Нахождение обратной матрицы является важной составляющей в разделе линейной алгебры. С помощью таких матриц, если они существуют, можно быстро найти решение системы линейных уравнений.
Матрицаназывается обратной к матрице,если выполняются следующие равенства.
.
Если определитель матрицыотличен от нуля, то матрицу называют не особо или невырожденной.
Для того, чтобы матрица имела обратную необходимо и достаточно, чтобы она была невырожденной
Алгоритм нахождения обратной матрицы
Пусть имеем квадратную матрицу
и нужно найти обратную к ней. Для этого нужно выполнить следующие действия:
1. Найти определитель матрицы. Если он не равен нулю то выполняем следующие действия. В противном случае данная матрица вырождена и для нее не существует обратной
2. Найти алгебраические дополнения элементов матрицы . Они равны минорам, умноженным на в степени суммы строки и столбца, для которого ищем.
3. Составить матрицу из алгебраических дополнений элементов матрицы матрицы и протранспонировать ее. Эта матрица называется присоединенной или союзной и обозначается .
4. Разделить присоединенную матрицу на детерминант . Полученная матрица будет обратной и иметь свойства, которые изложены в начале статьи.
——————————————–
Пример 1.
Найти матрицу, обратную к матрице (Дубовик В.П., Юрик И.И. “Высшая математика. Сборник задач”)
1) (1.127)
2) (1.130)
3) (1.133)
Решение.
1)Находим определитель матрицы
Так как детерминант не равен нулю (), то обратная матрица существует. Находим матрицу, составленную из алгебраических дополнений
Матрица дополнений примет вид
Транспонируем ее и получаем присоединенную
Разделим ее на определитель и получим обратную
Видим, что в случае, когда определитель равен единице присоединена и обратная матрицы совпадают.
2) Вычисляем определитель матрицы
Находим матрицу алгебраических дополнений
Конечный вид матрицы дополнений
Транспонируем ее и находим союзную матрицу
Находим обратную матрицу
3) Вычислим детерминант матрицы. Для этого разложим его на первую строчку. В результате получим два отличны от нуля слагаемые
Находим матрицу алгебраических дополнений. Расписание определителя проводим по строкам и столбцам, в которых больше нулевых элементов (обозначены черным цветом).
Конечный вид матрицы дополнений следующий
Транспонируем ее и находим присоединенную матрицу
Поскольку определитель матрицы равен единице то обратная матрица совпадает с присоединенной. Данный пример назад.
При вычислениях обратной матрицы типичными являются ошибки связанные с неправильными знаками при вычислении определителя и матрицы дополнений.
——————————————–
——————————
yukhym.com
Обратная матрица и методы ее вычисления
Запишем вспомогательную матрицу
и приведем её, с помощью элементарных преобразований, к матрице, в которой единичная матрица будет слева. Переставим местами первую и вторую строки
Прибавим ко второй строке первую строку, умноженную на а к третьей строке первую, умноженную на
Прибавим ко второй строке третью, умноженную на
Умножим вторую строку на
Прибавим к первой строке вторую, умноженную на а к третьей вторую, умноженную на
Разделим третью строку на 3
К первой строке прибавим третью, умноженную на
Тогда обратная матрица равна
ru.solverbook.com
Нахождение обратной матрицы: три алгоритма и примеры
Нахождение обратной матрицы
- методом алгебраических дополнений, при котором требуется находить определители и транспонировать матрицы;
- методом исключения неизвестных Гаусса, при котором требуется производить элементарные преобразования матриц (складывать строки, умножать строки на одно и то же число и т. д.).
Для особо любознательных существуют и другие методы, например, метод линейных преобразований. На этом уроке разберём три упомянутых метода и алгоритмы нахождения обратной матрицы этими методами.
Обратной матрицей, которую требуется отыскать для данной квадратной матрицы А, называется такая матрица
,
произведение на которую матрицы А справа является единичной матрицей, т.е,
. (1)
Обратной матрицей, которую требуется отыскать для данной квадратной матрицы А, называется такая матрица
,
произведение на которую матрицы А справа является единичной матрицей, т.е,
. (1)
Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны единице.
Теорема. Для каждой неособенной (невырожденной, несингулярной) квадратной матрицы можно найти обратную матрицу, и притом только одну. Для особенной (вырожденной, сингулярной) квадратной матрицы обратная матрица не существует.
Квадратная матрица называется неособенной (или невырожденной, несингулярной), если её определитель не равен нулю, и особенной (или вырожденной, сингулярной), если её определитель равен нулю.
Для обратной матрицы существует уместная аналогия с обратным числом. Для каждого числа a, не равного нулю, существует такое число b, что произведение a и b равно единице: ab = 1. Число b называется обратным для числа b. Например, для числа 7 обратным является число 1/7, так как 7*1/7=1.
Для неособенной квадратной матрицы А обратной является матрица
, (2)
где – определитель матрицы А, а – матрица, союзная с матрицей А.
Алгоритм нахождения обратной матрицы методом алгебраических дополнений1. Найти определитель данной матрицы A. Если определитель равен нулю, нахождение обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.
2. Найти матрицу, транспонированную относительно A.
3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.
4. Применить формулу (2): умножить число, обратное определителю матрицы A, на союзную матрицу, найденную на шаге 4.
5. Проверить полученный на шаге 4 результат, умножив данную матрицу A на обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была найдена верно. В противном случае начать процесс решения снова.
Пример 1.
найти обратную матрицу.
Решение. Для нахождения обратной матрицы необходимо найти определитель матрицы А . Находим по правилу треугольников:
Следовательно, матрица А – неособенная (невырожденная, несингулярная) и для неё существует обратная.
Найдём матрицу, союзную с данной матрицей А.
Найдём матрицу , транспонированную относительно матрицы A:
Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы, транспонированной относительно матрицы A:
Следовательно, матрица , союзная с матрицей A, имеет видЗамечание. Порядок вычисления элементов и транспонирования матрицы может быть иным. Можно сначала вычислить алгебраические дополнения матрицы A, а затем транспонировать матрицу алгебраических дополнений. В результате должны получиться те же элементы союзной матрицы.
Применяя формулу (2), находим матрицу, обратную матрице А:
Алгоритм нахождения обратной матрицы методом исключения неизвестных Гаусса
1. К матрице A приписать единичную матрицу того же порядка.
2. Полученную сдвоенную матрицу преобразовать так, чтобы в левой её части получилась
единичная матрица, тогда в правой части на месте
единичной матрицы автоматически получится обратная матрица. Матрица
2. Если в процессе преобразования матрицы A в единичную матрицу в какой-либо строке или в каком-либо столбце окажутся только нули, то определитель матрицы равен нулю, и, следовательно, матрица A будет вырожденной, и она не имеет обратной матрицы. В этом случае дальнейшее нахождение обратной матрицы прекращается.
Пример 2. Для матрицы
найти обратную матрицу.
Решение. Составляем сдвоенную матрицу
и будем её преобразовывать, так чтобы в левой части получилась единичная матрица. Начинаем преобразования.
Умножим первую строку левой и правой матрицы на (-3) и сложим её со второй строкой, а затем умножим первую строку на (-4) и сложим её с третьей строкой, тогда получим
.
Чтобы по возможности не было дробных чисел при последующих преобразованиях, создадим предварительно единицу во второй строке в левой части сдвоенной матрицы. Для этого умножим вторую строку на 2 и вычтем из неё третью строку, тогда получим
.
Сложим первую строку со второй, а затем умножим вторую строку на (-9) и сложим её с третьей строкой. Тогда получим
.
Разделим третью строку на 8, тогда
.
Умножим третью строку на 2 и сложим её со второй строкой. Получается:
.
Переставим местами вторую и третью строку, тогда окончательно получим:
.
Видим, что в левой части получилась единичная матрица, следовательно, в правой части получилась обратная матрица . Таким образом:
.
Можно проверить правильность вычислений, умножим исходную матрицу на найденную обратную матрицу:
.
В результате должна получиться обратная матрица.
Пример 3. Для матрицы
найти обратную матрицу.
Решение. Составляем сдвоенную матрицу
и будем её преобразовывать.
Первую строку умножаем на 3, а вторую на 2, и вычитаем из второй, а затем первую строку умножаем на 5, а третью на 2 и вычитаем из третьей строки, тогда получим
.
Первую строку умножаем на 2 и складываем её со второй, а затем из третьей строки вычитаем вторую, тогда получим
.
Видим, что в третьей строке в левой части все элементы получились равными нулю. Следовательно, матрица вырожденная и обратной матрицы не имеет. Дальнейшее нахождение обратной марицы прекращаем.
Матрицы теснейшим образом связаны с системами линейных уравнений. Каждой матрице соответствует система линейных уравнений, коэффициенты в которой есть элементы матрицы. И наоборот, системе линейных уравнений соответствует некоторая матрица.
Поэтому существует метод линейных преобразований для нахождения обратной матрицы. Для решения задач нам будет достаточно знать, что линейное преобразование – это система линейных уравнений, вид которой будет приведён ниже в алгоритме.
Алгоритм нахождения обратной матрицы методом линейных преобразований
1. Для данной невырожденной матрицы A составить линейное преобразование – систему линейных уравнений вида
,
где aij – элементы
матрицы
2. Решить полученную систему относительно y – найти для предыдущего линейного преобразование обратное линейное преобразование
,
в котором Aij – алгебраические дополнения элементов матрицы A, Δ – определитель матрицы A. Внимание! Алгебраические дополнения располагаются как в транспонированной матрице, то есть для элементов строки – в столбце, а для элементов столбца – в строке.
3. Находим коэффициенты при y: , которые и будут элементами матрицы, обратной для матрицы A.
4. Пользуясь элементами, найденными на шаге 3, записать найденную обратную матрицу.
Наиболее наблюдательные могли заметить, что по сути метод линейных преобразований – это тот же метод алгебраических преобразований (союзной матрицы), но с другой формой записи. Для кого-то метод линейных преобразований может оказаться более удобным как более компактный.
Пример 4. Найти обратную матрицу для матрицы
.
Сначала проверим, не равен ли нулю определитель данной матрицы. Он не равен нулю, следовательно, обратная матрица существует.
Для данной матрицы записываем линейное преобразование:
.
Находим линейное преобразование, обратное предыдущему, для этого потребуется находить алгебраические дополнения (урок откроется в новом окне). Запишем обратное линейное преобразование:
Коэффициенты при иксах в обратном линейном преобразовании – это элементы обратной матрицы для матрицы A. Таким образом нашли обратную матрицу:
Начало темы “Матрицы”
Другие темы линейной алгебры
function-x.ru
Обратные матрицы – Как найти обратную матрицу
Каталин Дэвид
Матрица обратима, если ее определитель отличен от нуля. Если A – обратимая матрица, то обратная ей матрица есть $A^{-1}=\frac{1}{\left|A\right|} \cdot adj(A)$. $adj(A)$ – присоединённая матрица исходной матрицы A.
Вычисление обратной матрицы
- Вычисляем определитель матрицы.
- Записываем транспонированную матрицу.
- Заменяем каждый элемент транспонированной матрицы его алгебраическим дополнением. Полученная матрица является присоединённой матрицей.
- Вычисляем обратную матрицу.
Пример 46
$A=\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}$
$\left|A\right|=1\cdot 5-6=-1$
Матрица обратима, значит, можно найти обратную ей матрицу.
$ A^{T}= \begin{pmatrix} 1 & 2\\ 3 & 5 \end{pmatrix}$
Заменяем элементы транспонированной матрицы их алгебраическими дополнениями.
$1\longrightarrow (-1)^{1+1}\cdot \Delta_{1,1}=(-1)^{2}\cdot5 = 5$
$2\longrightarrow (-1)^{1+2}\cdot \Delta_{1,2}=(-1)^{3}\cdot3 = -3$
$3\longrightarrow (-1)^{2+1}\cdot \Delta_{2,1}=(-1)^{3}\cdot2 = -2$
$5\longrightarrow (-1)^{2+2}\cdot \Delta_{2,2}=(-1)^{4}\cdot1 = 1$
$adj(A)= \begin{pmatrix} 5 & -3\\ -2 & 1\\ \end{pmatrix}$
$A^{-1}=- \begin{pmatrix} 5 & -3\\ -2 & 1 \end{pmatrix} = \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}$
Пример 47
$B=\begin{pmatrix} 2 & -7\\ -1 & 6 \end{pmatrix}$
$\left|B\right|=2\cdot 6-(-7)\cdot (-1) = 5$
Матрица обратима, значит, можно найти обратную ей матрицу.
$A^{T}= \begin{pmatrix} 2 & -1\\ -7 & 6 \end{pmatrix}$
Заменяем элементы транспонированной матрицы их алгебраическими дополнениями.
$2\longrightarrow (-1)^{1+1}\cdot \Delta_{1,1}=(-1)^{2}\cdot6 = 6$
$-1\longrightarrow (-1)^{1+2}\cdot \Delta_{1,2}=(-1)^{3}\cdot(-7) = 7$
$-7\longrightarrow (-1)^{2+1}\cdot \Delta_{2,1}=(-1)^{3}\cdot(-1) = 1$
$6\longrightarrow (-1)^{2+2}\cdot \Delta_{2,2}=(-1)^{4}\cdot2 = 2$
$adj(A)= \begin{pmatrix} 6 & 7\\ 1 & 2 \end{pmatrix}$
$A^{-1}=\frac{1}{5} \begin{pmatrix} 6 & 7\\ 1 & 2 \end{pmatrix} = \begin{pmatrix} \frac{6}{5} & \frac{7}{5}\\ \frac{1}{5} & \frac{2}{5} \end{pmatrix}$
Пример 48
$C=\begin{pmatrix} 1 & 3 & 2\\ 4 & 1 & 1\\ 1 & 2 & 3\\ \end{pmatrix}$
Вычисляем определитель по известной формуле и получаем $\left|B\right|=-18$.
Матрица обратима, значит, можно найти обратную ей матрицу.
$C^{T}=\begin{pmatrix} 1 & 4 & 1\\ 3 & 1 & 2\\ 2 & 1 & 3 \end{pmatrix}$
Заменяем каждый элемент транспонированной матрицы его алгебраическим дополнением.
$ 1\longrightarrow (-1)^{1+1}\cdot \Delta_{1,1}=(-1)^{2}\cdot \begin{vmatrix} 1 & 2\\ 1 & 3 \end{vmatrix} = 3 – 2 = 1$
$4\longrightarrow (-1)^{1+2}\cdot \Delta_{1,2}=(-1)^{3}\cdot \begin{vmatrix} 3 & 2\\ 2 & 3 \end{vmatrix} = -(9-4)=-5$
$1\longrightarrow (-1)^{1+3}\cdot \Delta_{1,3}=(-1)^{4}\cdot \begin{vmatrix} 3 & 1\\ 2 & 1 \end{vmatrix} = 3-2=1$
$3\longrightarrow (-1)^{2+1}\cdot \Delta_{2,1}=(-1)^{3}\cdot \begin{vmatrix} 4 & 1\\ 1 & 3\\ \end{vmatrix} = -(12-1)=-11$
$1\longrightarrow (-1)^{2+2}\cdot \Delta_{2,2}=$ $(-1)^{4}\cdot\begin{vmatrix} 1 & 1\\ 2 & 3\\ \end{vmatrix}=3-2=1$
$2\longrightarrow (-1)^{1+3}\cdot \Delta_{2,3}=$ $(-1)^{5}\cdot\begin{vmatrix} 1 & 4\\ 2 & 1 \end{vmatrix}= -(1-8)=7$
$2\longrightarrow (-1)^{3+1}\cdot \Delta_{3,1}=$ $(-1)^{4}\cdot\begin{vmatrix} 4 & 1\\ 1 & 2 \end{vmatrix}=8-1=7$
$1\longrightarrow (-1)^{3+2}\cdot \Delta_{3,2}=$ $(-1)^{5}\cdot \begin{vmatrix} 1 & 1\\ 3 & 2 \end{vmatrix}=-(2-3)=1$
$3\longrightarrow (-1)^{3+3}\cdot \Delta_{3,3}=$ $(-1)^{6}\cdot\begin{vmatrix} 1 & 4\\ 3 & 1 \end{vmatrix}=1-12=-11$
$adj(A)= \begin{pmatrix} 1 & -5 & 1\\ -11 & 1 & 7\\ 7 & 1 & -11 \end{pmatrix}$
$A^{-1} = – \frac{1}{18}\cdot \begin{pmatrix} 1 & -5 & 1\\ -11 & 1 & 7\\ 7 & 1 & -11 \end{pmatrix} =$ $\begin{pmatrix} – \frac{1}{18} & \frac{5}{18} & -\frac{1}{18}\\ \frac{11}{18} & -\frac{1}{18} & -\frac{7}{18}\\ -\frac{7}{18} & -\frac{1}{18} & \frac{11}{18} \end{pmatrix}$
Свойства обратной матрицы
Если A – обратимая матрица, то:
$A\cdot A^{-1} = A^{-1}\cdot A=I_{n}$
Пример 49
$A=\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}$
$A^{-1}= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}$
$A\cdot A^{-1}= \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix} \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}=$ $\begin{pmatrix} 1\cdot(-5)+3\cdot2 & 1\cdot3 + 3\cdot(-1)\\ 2\cdot(-5)+5\cdot2 & 2\cdot3 +5\cdot(-1) \end{pmatrix} = \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix}= I_{2}$
$A^{-1}\cdot A= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix} \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}=$ $\begin{pmatrix} -5\cdot1 + 3\cdot2 & -5\cdot3 + 3\cdot 5\\ 2\cdot1 +(-1)\cdot2 & 2\cdot3 +(-1)\cdot5 \end{pmatrix}= \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix}=I_{2}$
www.math10.com
Лекция 5. Обратная матрица
Обратные матрицы. Лекция 5.
Обратная матрица.
Квадратная матрица называетсяневырожденной, если её определитель не равен 0. В противном случае матрица называется вырожденной.
Матрица называетсяобратной к матрице , если выполняется следующее условие:. В этом случае обозначают.
Теорема 1. Всякая невырожденная матрица имеет свою обратную матрицу. Доказательство. Пусть дана матрица , причем. Составим матрицуследующим образом
,
где – алгебраические дополнения соответствующих элементовматрицы. Найдем произведение
На диагонали полученной матрицы стоят суммы произведений элементов строк на их алгебраические дополнения. По свойству 8 они равны определителю матрицы . На остальных местах стоят суммы произведений элементов строк на соответствующие алгебраические дополнения элементов других строк. По свойству 9 все они равны нулю. Поэтому
. Таким образом, . Аналогично можно получить равенство. Отсюда
По определению обратной матрицы
Так как , то матрицасуществует. Следовательно, матрицаимеет обратную матрицу. Теорема доказана.
Следствие: Для произвольной матрицы обратная матрица имеет вид .
Есть другой способ вычисления обратной матрицы методом элементарных преобразований. Для матрицы и единичной матрицысоставляется расширенная матрица, которая с помощью элементарных преобразований приводится к виду. Можно показать, что в этом случае.
Пример 25. Для матриц ивычислитьи.
Решение. Так как , то обратная матрица существует. Найдем алгебраические дополнения:
, ,,.
В соответствии с следствием из теоремы о существовании обратной матрицы . Сделаем проверку
.
Так как , то обратная матрица существует. Найдем алгебраические дополнения:
.
В соответствии с следствием из теоремы о существовании обратной матрицы . Сделаем проверку
Ответ:
Свойства обратной матрицы.
;
;
.
Ранг матрицы.
Пусть дана матрица размерности
.
Выделим в ней строк истолбцов.. Из элементов, стоящих на пересечениистрок истолбцов составим определитель– го порядка. Все такие определители называютминорами матрицы.
Пример 26. Для матрицы минорами второго порядка будут, например, определители
, ,,,,,,,.
Минорами третьего порядка – ,,,.
Всего для матрицы можно составитьминоров порядка, где. Так для матрицысуществует всего
миноров второго порядка.
Наибольший из порядков минора данной матрицы, отличных от нуля называется рангом матрицы. Обозначаются как .
Минор, порядок которого равен рангу матрицы, называют базисным минором. У каждой матрицы может быть несколько базисных миноров.
Свойства ранга матрицы.
1. При транспонировании матрицы её ранг не меняется.
2. Если из матрицы убрать нулевую строку (нулевой столбец), то ранг матрицы не изменится.
3. Ранг матрицы не меняется при её элементарных преобразованиях.
4. Ранг матрицы равен числу не нулевых строк в её ступенчатом виде.
27
studfiles.net
Обратная матрица
Эта тема является одной из самых ненавистных среди студентов. Хуже, наверное, только определители.
Фишка в том, что само понятие обратного элемента (и я сейчас не только о матрицах) отсылает нас к операции умножения. Даже в школьной программе умножение считается сложной операцией, а уж умножение матриц — вообще отдельная тема, которой у меня посвящён целый параграф и видеоурок.
Сегодня мы не будем вдаваться в подробности матричных вычислений. Просто вспомним: как обозначаются матрицы, как они умножаются и что из этого следует.
Повторение: умножение матриц
Прежде всего договоримся об обозначениях. Матрицей $A$ размера $\left[ m\times n \right]$ называется просто таблица из чисел, в которой ровно $m$ строк и $n$ столбцов:
\[A=\left[ m\times n \right]=\underbrace{\left[ \begin{matrix} {{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} \\ {{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} \\ … & … & … & … \\ {{a}_{m1}} & {{a}_{m2}} & … & {{a}_{mn}} \\\end{matrix} \right]}_{n}\]
Чтобы случайно не перепутать строки и столбцы местами (поверьте, на экзамене можно и единицу с двойкой перепутать — что уж говорить про какие-то там строки), просто взгляните на картинку:
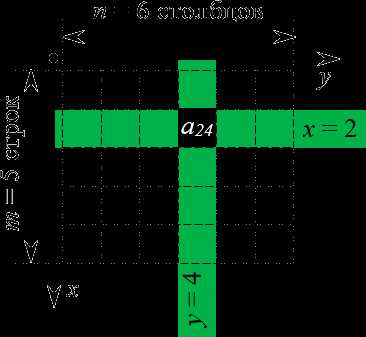Определение индексов для клеток матрицыЧто происходит? Если разместить стандартную систему координат $OXY$ в левом верхнем углу и направить оси так, чтобы они охватывали всю матрицу, то каждой клетке этой матрицы можно однозначно сопоставить координаты $\left( x;y \right)$ — это и будет номер строки и номер столбца.
Почему система координат размещена именно в левом верхнем углу? Да потому что именно оттуда мы начинаем читать любые тексты. Это очень просто запомнить.
А почему ось $x$ направлена именно вниз, а не вправо? Опять всё просто: возьмите стандартную систему координат (ось $x$ идёт вправо, ось $y$ — вверх) и поверните её так, чтобы она охватывала матрицу. Это поворот на 90 градусов по часовой стрелке — его результат мы и видим на картинке.
В общем, как определять индексы у элементов матрицы, мы разобрались. Теперь давайте разберёмся с умножением.
Определение. Матрицы $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$, когда количество столбцов в первой совпадает с количеством строк во второй, называются согласованными.
Именно в таком порядке. Можно сумничать и сказать, мол, матрицы $A$ и $B$ образуют упорядоченную пару $\left( A;B \right)$: если они согласованы в таком порядке, то совершенно необязательно, что $B$ и $A$, т.е. пара $\left( B;A \right)$ — тоже согласована.
Умножать можно только согласованные матрицы.
Определение. Произведение согласованных матриц $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$ — это новая матрица $C=\left[ m\times k \right]$, элементы которой ${{c}_{ij}}$ считаются по формуле:
\[{{c}_{ij}}=\sum\limits_{k=1}^{n}{{{a}_{ik}}}\cdot {{b}_{kj}}\]
Другими словами: чтобы получить элемент ${{c}_{ij}}$ матрицы $C=A\cdot B$, нужно взять $i$-строку первой матрицы, $j$-й столбец второй матрицы, а затем попарно перемножить элементы из этой строки и столбца. Результаты сложить.
Да, вот такое суровое определение. Из него сразу следует несколько фактов:
- Умножение матриц, вообще говоря, некоммутативно: $A\cdot B\ne B\cdot A$;
- Однако умножение ассоциативно: $\left( A\cdot B \right)\cdot C=A\cdot \left( B\cdot C \right)$;
- И даже дистрибутивно: $\left( A+B \right)\cdot C=A\cdot C+B\cdot C$;
- И ещё раз дистрибутивно: $A\cdot \left( B+C \right)=A\cdot B+A\cdot C$.
Дистрибутивность умножения пришлось отдельно описывать для левого и правого множителя-суммы как раз из-за некоммутативности операции умножения.
Если всё же получается так, что $A\cdot B=B\cdot A$, такие матрицы называются перестановочными.
Среди всех матриц, которые там на что-то умножаются, есть особые — те, которые при умножении на любую матрицу $A$ снова дают $A$:
Определение. Матрица $E$ называется единичной, если $A\cdot E=A$ или $E\cdot A=A$. В случае с квадратной матрицей $A$ можем записать:
\[A\cdot E=E\cdot A=A\]
Единичная матрица — частый гость при решении матричных уравнений. И вообще частый гость в мире матриц.:)
А ещё из-за этой $E$ кое-кто придумал всю ту дичь, которая будет написана дальше.
Что такое обратная матрица
Поскольку умножение матриц — весьма трудоёмкая операция (приходится перемножать кучу строчек и столбцов), то понятие обратной матрицы тоже оказывается не самым тривиальным. И требующим некоторых пояснений.
Ключевое определение
Что ж, пора познать истину.
Определение. Матрица $B$ называется обратной к матрице $A$, если
\[A\cdot B=B\cdot A=E\]
Обратная матрица обозначается через ${{A}^{-1}}$ (не путать со степенью!), поэтому определение можно переписать так:
\[A\cdot {{A}^{-1}}={{A}^{-1}}\cdot A=E\]
Казалось бы, всё предельно просто и ясно. Но при анализе такого определения сразу возникает несколько вопросов:
- Всегда ли существует обратная матрица? И если не всегда, то как определить: когда она существует, а когда — нет?
- А кто сказал, что такая матрица ровно одна? Вдруг для некоторой исходной матрицы $A$ найдётся целая толпа обратных?
- Как выглядят все эти «обратные»? И как, собственно, их считать?
Насчёт алгоритмов вычисления — об этом мы поговорим чуть позже. Но на остальные вопросы ответим прямо сейчас. Оформим их в виде отдельных утверждений-лемм.
Основные свойства
Начнём с того, как в принципе должна выглядеть матрица $A$, чтобы для неё существовала ${{A}^{-1}}$. Сейчас мы убедимся в том, что обе эти матрицы должны быть квадратными, причём одного размера: $\left[ n\times n \right]$.
Лемма 1. Дана матрица $A$ и обратная ей ${{A}^{-1}}$. Тогда обе эти матрицы — квадратные, причём одинакового порядка $n$.
Доказательство. Всё просто. Пусть матрица $A=\left[ m\times n \right]$, ${{A}^{-1}}=\left[ a\times b \right]$. Поскольку произведение $A\cdot {{A}^{-1}}=E$ по определению существует, матрицы $A$ и ${{A}^{-1}}$ согласованы в указанном порядке:
\[\begin{align} & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end{align}\]
Это прямое следствие из алгоритма перемножения матриц: коэффициенты $n$ и $a$ являются «транзитными» и должны быть равны.
Вместе с тем определено и обратное умножение: ${{A}^{-1}}\cdot A=E$, поэтому матрицы ${{A}^{-1}}$ и $A$ тоже согласованы в указанном порядке:
\[\begin{align} & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end{align}\]
Таким образом, без ограничения общности можем считать, что $A=\left[ m\times n \right]$, ${{A}^{-1}}=\left[ n\times m \right]$. Однако согласно определению $A\cdot {{A}^{-1}}={{A}^{-1}}\cdot A$, поэтому размеры матриц строго совпадают:
\[\begin{align} & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end{align}\]
Вот и получается, что все три матрицы — $A$, ${{A}^{-1}}$ и $E$ — являются квадратными размером $\left[ n\times n \right]$. Лемма доказана.
Что ж, уже неплохо. Мы видим, что обратимыми бывают лишь квадратные матрицы. Теперь давайте убедимся, что обратная матрица всегда одна.
Лемма 2. Дана матрица $A$ и обратная ей ${{A}^{-1}}$. Тогда эта обратная матрица — единственная.
Доказательство. Пойдём от противного: пусть у матрицы $A$ есть хотя бы два экземпляра обратных —$B$ и $C$. Тогда, согласно определению, верны следующие равенства:
\[\begin{align} & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end{align}\]
Из леммы 1 мы заключаем, что все четыре матрицы — $A$, $B$, $C$ и $E$ — являются квадратными одинакового порядка: $\left[ n\times n \right]$. Следовательно, определено произведение:
\[B\cdot A\cdot C\]
Поскольку умножение матриц ассоциативно (но не коммутативно!), мы можем записать:
\[\begin{align} & B\cdot A\cdot C=\left( B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left( A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Rightarrow B=C. \\ \end{align}\]
Получили единственно возможный вариант: два экземпляра обратной матрицы равны. Лемма доказана.
Приведённые рассуждения почти дословно повторяют доказательство единственность обратного элемента для всех действительных чисел $b\ne 0$. Единственное существенное дополнение — учёт размерности матриц.
Впрочем, мы до сих пор ничего не знаем о том, всякая ли квадратная матрица является обратимой. Тут нам на помощь приходит определитель — это ключевая характеристика для всех квадратных матриц.
Лемма 3. Дана матрица $A$. Если обратная к ней матрица ${{A}^{-1}}$ существует, то определитель исходной матрицы отличен от нуля:
\[\left| A \right|\ne 0\]
Доказательство. Мы уже знаем, что $A$ и ${{A}^{-1}}$ — квадратные матрицы размера $\left[ n\times n \right]$. Следовательно, для каждой из них можно вычислить определитель: $\left| A \right|$ и $\left| {{A}^{-1}} \right|$. Однако определитель произведения равен произведению определителей:
\[\left| A\cdot B \right|=\left| A \right|\cdot \left| B \right|\Rightarrow \left| A\cdot {{A}^{-1}} \right|=\left| A \right|\cdot \left| {{A}^{-1}} \right|\]
Но согласно определению $A\cdot {{A}^{-1}}=E$, а определитель $E$ всегда равен 1, поэтому
\[\begin{align} & A\cdot {{A}^{-1}}=E; \\ & \left| A\cdot {{A}^{-1}} \right|=\left| E \right|; \\ & \left| A \right|\cdot \left| {{A}^{-1}} \right|=1. \\ \end{align}\]
Произведение двух чисел равно единице только в том случае, когда каждое из этих чисел отлично от нуля:
\[\left| A \right|\ne 0;\quad \left| {{A}^{-1}} \right|\ne 0.\]
Вот и получается, что $\left| A \right|\ne 0$. Лемма доказана.
На самом деле это требование вполне логично. Сейчас мы разберём алгоритм нахождения обратной матрицы — и станет совершенно ясно, почему при нулевом определителе никакой обратной матрицы в принципе не может существовать.
Но для начала сформулируем «вспомогательное» определение:
Определение. Вырожденная матрица — это квадратная матрица размера $\left[ n\times n \right]$, чей определитель равен нулю.
Таким образом, мы можем утверждать, что всякая обратимая матрица является невырожденной.
Как найти обратную матрицу
Сейчас мы рассмотрим универсальный алгоритм нахождения обратных матриц. Вообще, существует два общепринятых алгоритма, и второй мы тоже сегодня рассмотрим.
Тот, который будет рассмотрен сейчас, очень эффективен для матриц размера $\left[ 2\times 2 \right]$ и — частично — размера $\left[ 3\times 3 \right]$. А вот начиная с размера $\left[ 4\times 4 \right]$ его лучше не применять. Почему — сейчас сами всё поймёте.
Алгебраические дополнения
Готовьтесь. Сейчас будет боль. Нет, не переживайте: к вам не идёт красивая медсестра в юбке, чулках с кружевами и не сделает укол в ягодицу. Всё куда прозаичнее: к вам идут алгебраические дополнения и Её Величество «Союзная Матрица».
Начнём с главного. Пусть имеется квадратная матрица размера $A=\left[ n\times n \right]$, элементы которой именуются ${{a}_{ij}}$. Тогда для каждого такого элемента можно определить алгебраическое дополнение:
Определение. Алгебраическое дополнение ${{A}_{ij}}$ к элементу ${{a}_{ij}}$, стоящего в $i$-й строке и $j$-м столбце матрицы $A=\left[ n\times n \right]$ — это конструкция вида
\[{{A}_{ij}}={{\left( -1 \right)}^{i+j}}\cdot M_{ij}^{*}\]
Где $M_{ij}^{*}$ — определитель матрицы, полученной из исходной $A$ вычёркиванием той самой $i$-й строки и $j$-го столбца.
Ещё раз. Алгебраическое дополнение к элементу матрицы с координатами $\left( i;j \right)$ обозначается как ${{A}_{ij}}$ и считается по схеме:
- Сначала вычёркиваем из исходной матрицы $i$-строчку и $j$-й столбец. Получим новую квадратную матрицу, и её определитель мы обозначаем как $M_{ij}^{*}$.
- Затем умножаем этот определитель на ${{\left( -1 \right)}^{i+j}}$ — поначалу это выражение может показаться мозговыносящим, но по сути мы просто выясняем знак перед $M_{ij}^{*}$.
- Считаем — получаем конкретное число. Т.е. алгебраическое дополнение — это именно число, а не какая-то новая матрица и т.д.
Саму матрицу $M_{ij}^{*}$ называют дополнительным минором к элементу ${{a}_{ij}}$. И в этом смысле приведённое выше определение алгебраического дополнения является частным случаем более сложного определения — того, что мы рассматривали в уроке про определитель.
Важное замечание. Вообще-то во «взрослой» математике алгебраические дополнения определяются так:
- Берём в квадратной матрице $k$ строчек и $k$ столбцов. На их пересечении получится матрица размера $\left[ k\times k \right]$ — её определитель называется минором порядка $k$ и обозначается ${{M}_{k}}$.
- Затем вычёркиваем эти «избранные» $k$ строчек и $k$ столбцов. Снова получится квадратная матрица — её определитель называется дополнительным минором и обозначается $M_{k}^{*}$.
- Умножаем $M_{k}^{*}$ на ${{\left( -1 \right)}^{t}}$, где $t$ — это (вот сейчас внимание!) сумма номеров всех выбранных строчек и столбцов. Это и будет алгебраическое дополнение.
Взгляните на третий шаг: там вообще-то сумма $2k$ слагаемых! Другое дело, что для $k=1$ мы получим лишь 2 слагаемых — это и будут те самые $i+j$ — «координаты» элемента ${{a}_{ij}}$, для которого мы ищем алгебраическое дополнение.
Таким образом сегодня мы используем слегка упрощённое определение. Но как мы увидим в дальнейшем, его окажется более чем достаточно. Куда важнее следующая штука:
Определение. Союзная матрица $S$ к квадратной матрице $A=\left[ n\times n \right]$ — это новая матрица размера $\left[ n\times n \right]$, которая получается из $A$ заменой ${{a}_{ij}}$ алгебраическими дополнениями ${{A}_{ij}}$:
\[A=\left[ \begin{matrix} {{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} \\ {{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} \\ … & … & … & … \\ {{a}_{n1}} & {{a}_{n2}} & … & {{a}_{nn}} \\\end{matrix} \right]\Rightarrow S=\left[ \begin{matrix} {{A}_{11}} & {{A}_{12}} & … & {{A}_{1n}} \\ {{A}_{21}} & {{A}_{22}} & … & {{A}_{2n}} \\ … & … & … & … \\ {{A}_{n1}} & {{A}_{n2}} & … & {{A}_{nn}} \\\end{matrix} \right]\]
Первая мысль, возникающая в момент осознания этого определения — «это сколько же придётся всего считать!» Расслабьтесь: считать придётся, но не так уж и много.:)
Что ж, всё это очень мило, но зачем это нужно? А вот зачем.
Основная теорема
Вернёмся немного назад. Помните, в Лемме 3 утверждалось, что обратимая матрица $A$ всегда не вырождена (т.е. её определитель отличен от нуля: $\left| A \right|\ne 0$).
Так вот, верно и обратное: если матрица $A$ не вырождена, то она всегда обратима. И даже существует схема поиска ${{A}^{-1}}$. Зацените:
Теорема об обратной матрице. Пусть дана квадратная матрица $A=\left[ n\times n \right]$, причём её определитель отличен от нуля: $\left| A \right|\ne 0$. Тогда обратная матрица ${{A}^{-1}}$ существует и считается по формуле:
\[{{A}^{-1}}=\frac{1}{\left| A \right|}\cdot {{S}^{T}}\]
А теперь — всё то же самое, но разборчивым почерком. Чтобы найти обратную матрицу, нужно:
- Посчитать определитель $\left| A \right|$ и убедиться, что он отличен от нуля.
- Составить союзную матрицу $S$, т.е. посчитать 100500 алгебраических дополнений ${{A}_{ij}}$ и расставить их на месте ${{a}_{ij}}$.
- Транспонировать эту матрицу $S$, а затем умножить её на некое число $q={1}/{\left| A \right|}\;$.
И всё! Обратная матрица ${{A}^{-1}}$ найдена. Давайте посмотрим на примеры:
Задача. Найдите обратную матрицу:
\[\left[ \begin{matrix} 3 & 1 \\ 5 & 2 \\\end{matrix} \right]\]
Решение. Проверим обратимость. Посчитаем определитель:
\[\left| A \right|=\left| \begin{matrix} 3 & 1 \\ 5 & 2 \\\end{matrix} \right|=3\cdot 2-1\cdot 5=6-5=1\]
Определитель отличен от нуля. Значит, матрица обратима. Составим союзную матрицу:
\[S=\left[ \begin{matrix} {{A}_{11}} & {{A}_{12}} \\ {{A}_{21}} & {{A}_{22}} \\\end{matrix} \right]\]
Посчитаем алгебраические дополнения:
\[\begin{align} & {{A}_{11}}={{\left( -1 \right)}^{1+1}}\cdot \left| 2 \right|=2; \\ & {{A}_{12}}={{\left( -1 \right)}^{1+2}}\cdot \left| 5 \right|=-5; \\ & {{A}_{21}}={{\left( -1 \right)}^{2+1}}\cdot \left| 1 \right|=-1; \\ & {{A}_{22}}={{\left( -1 \right)}^{2+2}}\cdot \left| 3 \right|=3. \\ \end{align}\]
Обратите внимание: определители |2|, |5|, |1| и |3| — это именно определители матриц размера $\left[ 1\times 1 \right]$, а не модули. Т.е. если в определителях стояли отрицательные числа, убирать «минус» не надо.
Итого наша союзная матрица выглядит так:
\[S=\left[ \begin{array}{*{35}{r}}2 & -5 \\ -1 & 3 \\\end{array} \right]\]
Осталось посчитать обратную:
\[{{A}^{-1}}=\frac{1}{\left| A \right|}\cdot {{S}^{T}}=\frac{1}{1}\cdot {{\left[ \begin{array}{*{35}{r}} 2 & -5 \\ -1 & 3 \\\end{array} \right]}^{T}}=\left[ \begin{array}{*{35}{r}} 2 & -1 \\ -5 & 3 \\\end{array} \right]\]
Ну вот и всё. Задача решена.
Ответ. $\left[ \begin{array}{*{35}{r}} 2 & -1 \\ -5 & 3 \\\end{array} \right]$
Задача. Найдите обратную матрицу:
\[\left[ \begin{array}{*{35}{r}} 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end{array} \right]\]
Решение. Опять считаем определитель:
\[\begin{align} & \left| \begin{array}{*{35}{r}} 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end{array} \right|=\begin{matrix} \left( 1\cdot 2\cdot 1+\left( -1 \right)\cdot \left( -1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left( 2\cdot 2\cdot 1+\left( -1 \right)\cdot 0\cdot 1+1\cdot \left( -1 \right)\cdot 0 \right) \\\end{matrix}= \\ & =\left( 2+1+0 \right)-\left( 4+0+0 \right)=-1\ne 0. \\ \end{align}\]
Определитель отличен от нуля — матрица обратима. А вот сейчас будет самая жесть: надо посчитать аж 9 (девять, мать их!) алгебраических дополнений. И каждое из них будет содержать определитель $\left[ 2\times 2 \right]$. Полетели:
\[\begin{matrix} {{A}_{11}}={{\left( -1 \right)}^{1+1}}\cdot \left| \begin{matrix} 2 & -1 \\ 0 & 1 \\\end{matrix} \right|=2; \\ {{A}_{12}}={{\left( -1 \right)}^{1+2}}\cdot \left| \begin{matrix} 0 & -1 \\ 1 & 1 \\\end{matrix} \right|=-1; \\ {{A}_{13}}={{\left( -1 \right)}^{1+3}}\cdot \left| \begin{matrix} 0 & 2 \\ 1 & 0 \\\end{matrix} \right|=-2; \\ … \\ {{A}_{33}}={{\left( -1 \right)}^{3+3}}\cdot \left| \begin{matrix} 1 & -1 \\ 0 & 2 \\\end{matrix} \right|=2; \\ \end{matrix}\]
Короче, союзная матрица будет выглядеть так:
\[S=\left[ \begin{matrix} 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end{matrix} \right]\]
Следовательно, обратная матрица будет такой:
\[{{A}^{-1}}=\frac{1}{-1}\cdot \left[ \begin{matrix} 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end{matrix} \right]=\left[ \begin{array}{*{35}{r}}-2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end{array} \right]\]
Ну и всё. Вот и ответ.
Ответ. $\left[ \begin{array}{*{35}{r}} -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end{array} \right]$
Как видите, в конце каждого примера мы выполняли проверку. В связи с этим важное замечание:
Не ленитесь выполнять проверку. Умножьте исходную матрицу на найденную обратную — должна получиться $E$.
Выполнить эту проверку намного проще и быстрее, чем искать ошибку в дальнейших вычислениях, когда, например, вы решаете матричное уравнение.
Альтернативный способ
Как я и говорил, теорема об обратной матрице прекрасно работает для размеров $\left[ 2\times 2 \right]$ и $\left[ 3\times 3 \right]$ (в последнем случае — уже не так уж и «прекрасно»), а вот для матриц больших размеров начинается прям печаль.
Но не переживайте: есть альтернативный алгоритм, с помощью которого можно невозмутимо найти обратную хоть для матрицы $\left[ 10\times 10 \right]$. Но, как это часто бывает, для рассмотрения этого алгоритма нам потребуется небольшая теоретическая вводная.
Элементарные преобразования
Среди всевозможных преобразований матрицы есть несколько особых — их называют элементарными. Таких преобразований ровно три:
- Умножение. Можно взять $i$-ю строку (столбец) и умножить её на любое число $k\ne 0$;
- Сложение. Прибавить к $i$-й строке (столбцу) любую другую $j$-ю строку (столбец), умноженную на любое число $k\ne 0$ (можно, конечно, и $k=0$, но какой в этом смысл? Ничего не изменится же).
- Перестановка. Взять $i$-ю и $j$-ю строки (столбцы) и поменять местами.
Почему эти преобразования называются элементарными (для больших матриц они выглядят не такими уж элементарными) и почему их только три — эти вопросы выходят за рамки сегодняшнего урока. Поэтому не будем вдаваться в подробности.
Важно другое: все эти извращения нам предстоит выполнять над присоединённой матрицей. Да, да: вы не ослышались. Сейчас будет ещё одно определение — последнее в сегодняшнем уроке.
Присоединённая матрица
Наверняка в школе вы решали системы уравнений методом сложения. Ну, там, вычесть из одной строки другую, умножить какую-то строку на число — вот это вот всё.
Так вот: сейчас будет всё то же, но уже «по-взрослому». Готовы?
Определение. Пусть дана матрица $A=\left[ n\times n \right]$ и единичная матрица $E$ такого же размера $n$. Тогда присоединённая матрица $\left[ A\left| E \right. \right]$ — это новая матрица размера $\left[ n\times 2n \right]$, которая выглядит так:
\[\left[ A\left| E \right. \right]=\left[ \begin{array}{rrrr|rrrr}{{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} & 1 & 0 & … & 0 \\{{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} & 0 & 1 & … & 0 \\… & … & … & … & … & … & … & … \\{{a}_{n1}} & {{a}_{n2}} & … & {{a}_{nn}} & 0 & 0 & … & 1 \\\end{array} \right]\]
Короче говоря, берём матрицу $A$, справа приписываем к ней единичную матрицу $E$ нужного размера, разделяем их вертикальной чертой для красоты — вот вам и присоединённая.:)
В чём прикол? А вот в чём:
Теорема. Пусть матрица $A$ обратима. Рассмотрим присоединённую матрицу $\left[ A\left| E \right. \right]$. Если с помощью элементарных преобразований строк привести её к виду $\left[ E\left| B \right. \right]$, т.е. путём умножения, вычитания и перестановки строк получить из $A$ матрицу $E$ справа, то полученная слева матрица $B$ — это обратная к $A$:
\[\left[ A\left| E \right. \right]\to \left[ E\left| B \right. \right]\Rightarrow B={{A}^{-1}}\]
Вот так всё просто! Короче говоря, алгоритм нахождения обратной матрицы выглядит так:
- Записать присоединённую матрицу $\left[ A\left| E \right. \right]$;
- Выполнять элементарные преобразования строк до тех пор, пока права вместо $A$ не появится $E$;
- Разумеется, слева тоже что-то появится — некая матрица $B$. Это и будет обратная;
- PROFIT!:)
Конечно, сказать намного проще, чем сделать. Поэтому давайте рассмотрим парочку примеров: для размеров $\left[ 3\times 3 \right]$ и $\left[ 4\times 4 \right]$.
Задача. Найдите обратную матрицу:
\[\left[ \begin{array}{*{35}{r}} 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end{array} \right]\]
Решение. Составляем присоединённую матрицу:
\[\left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end{array} \right]\]
Поскольку последний столбец исходной матрицы заполнен единицами, вычтем первую строку из остальных:
\[\begin{align} & \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end{array} \right]\begin{matrix} \downarrow \\ -1 \\ -1 \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end{array} \right] \\ \end{align}\]
Больше единиц нет, кроме первой строки. Но её мы не трогаем, иначе в третьем столбце начнут «размножаться» только что убранные единицы.
Зато можем вычесть вторую строку дважды из последней — получим единицу в левом нижнем углу:
\[\begin{align} & \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end{array} \right]\begin{matrix} \ \\ \downarrow \\ -2 \\\end{matrix}\to \\ & \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right] \\ \end{align}\]
Теперь можно вычесть последнюю строку из первой и дважды из второй — таким образом мы «занулим» первый столбец:
\[\begin{align} & \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right]\begin{matrix} -1 \\ -2 \\ \uparrow \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right] \\ \end{align}\]
Умножим вторую строку на −1, а затем вычтем её 6 раз из первой и прибавим 1 раз к последней:
\[\begin{align} & \left[ \begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right]\begin{matrix} \ \\ \left| \cdot \left( -1 \right) \right. \\ \ \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right]\begin{matrix} -6 \\ \updownarrow \\ +1 \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end{array} \right] \\ \end{align}\]
Осталось лишь поменять местами строки 1 и 3:
\[\left[ \begin{array}{rrr|rrr} 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & -18 & 32 & -13 \\\end{array} \right]\]
Готово! Справа — искомая обратная матрица.
Ответ. $\left[ \begin{array}{*{35}{r}}4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end{array} \right]$
Задача. Найдите обратную матрицу:
\[\left[ \begin{matrix} 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\end{matrix} \right]\]
Решение. Снова составляем присоединённую:
\[\left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end{array} \right]\]
Немного позалимаем, попечалимся от того, сколько сейчас придётся считать… и начнём считать. Для начала «обнулим» первый столбец, вычитая строку 1 из строк 2 и 3:
\[\begin{align} & \left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end{array} \right]\begin{matrix} \downarrow \\ -1 \\ -1 \\ \ \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end{array} \right] \\ \end{align}\]
Наблюдаем слишком много «минусов» в строках 2—4. Умножим все три строки на −1, а затем «выжжем» третий столбец, вычитая строку 3 из остальных:
\[\begin{align} & \left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end{array} \right]\begin{matrix} \ \\ \left| \cdot \left( -1 \right) \right. \\ \left| \cdot \left( -1 \right) \right. \\ \left| \cdot \left( -1 \right) \right. \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\\end{array} \right]\begin{matrix} -2 \\ -1 \\ \updownarrow \\ -2 \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right] \\ \end{align}\]
Теперь самое время «поджарить» последний столбец исходной матрицы: вычитаем строку 4 из остальных:
\[\begin{align} & \left[ \begin{array}{rrrr|rrrr} 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right]\begin{matrix} +1 \\ -3 \\ -2 \\ \uparrow \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right] \\ \end{align}\]
Финальный бросок: «выжигаем» второй столбец, вычитая строку 2 из строки 1 и 3:
\[\begin{align} & \left[ \begin{array}{rrrr|rrrr} 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right]\begin{matrix} 6 \\ \updownarrow \\ -5 \\ \ \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right] \\ \end{align}\]
И снова слева единичная матрица, значит справа — обратная.:)
Ответ. $\left[ \begin{matrix} 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & -1 \\\end{matrix} \right]$
Ну вот и всё. Проверку сделайте сами — мне в лом.:)
Смотрите также:
- Как считать определитель матрицы
- Угол между двумя прямыми
- Тест к уроку «Сложение и вычитание дробей» (средний)
- Комбинаторика в задаче B6: легкий тест
- Тест по методу интервалов для строгих неравенств
- Формула простого процента: как найти исходное значение
www.berdov.com
1.3.4. Примеры решения задач по теме «Обратная матрица»
Задача 1.
Найти обратную матрицу для матрицы
И проверить выполнение условий А А-1 = А-1А = Е.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
Убедимся, что матрица А – невырожденная. ΔА = 1·4 – 2·(-1) ≠ 0, следовательно, А-1 существует.
Вычислим алгебраические дополнения к элементам А:
Применим способ вычисления обратной матрицы:
.
Не забудьте, что обратная матрица образована из алгебраических дополнений к элементам Транспонированной матрицы! |
Найдем произведения А А-1 и А-1А:
Таким образом, найденная матрица А-1 отвечает определению обратной матрицы.
Ответ: .
Задача 2.
Найти обратную матрицу для матрицы
.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
Следовательно, матрица А невырожденная, и обратная матрица существует.
Вычислим алгебраические дополнения к элементам матрицы А:
Обратная матрица имеет вид:
Ответ: .
Задача 3.
Найти обратную матрицу для матрицы
.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
Вычислим определитель матрицы А разложением по первому столбцу:
.
Следовательно, обратная матрица для матрицы А существует.
Найдем алгебраические дополнения к элементам матрицы А:
Значит,
.
Ответ: .
Задача 4.
Найти обратную матрицу для матрицы
.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
.
Ответ:
Задача 5.
При каких X, Y, Z матрица
Является обратной к матрице
Указание
Необходимым условием того, что В = А-1, является требование АВ = Е.
Решение
Проверим невырожденность матрицы А:
Необходимым условием того, что В = А-1, является требование АВ = Е.
Найдем АВ:
Для того, чтобы выполнялось условие АВ = Е, X, Y, Z должны быть решением системы уравнений
Проверим, будет ли равно единичной матрице произведение ВА:
Значит, при найденных значениях X, Y, Z В = А-1.
Ответ: X = -3, Y = -3, Z = 4.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
