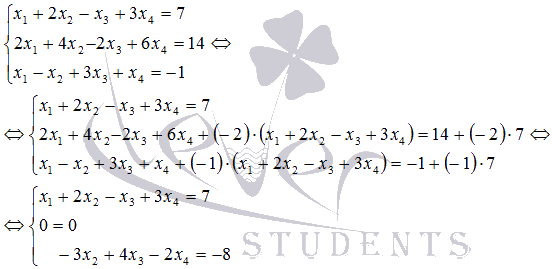
Метод исключения метод гаусса – Как решить методом Гаусса СЛАУ (систему линейных уровнений). Правила, примеры
- Комментариев к записи Метод исключения метод гаусса – Как решить методом Гаусса СЛАУ (систему линейных уровнений). Правила, примеры нет
- Советы абитуриенту
- Метод Гаусса (исключения неизвестных) — Мегаобучалка
- Метод последовательного исключения неизвестных. Метод Гаусса.
- 1.6 Метод Гаусса (метод последовательного исключения неизвестных)
- Тема 3 Метод последовательного исключения неизвестных (метод Гаусса)
- Метод Гаусса. Метод последовательного исключения неизвестных
- 3.2 Метод исключения Гаусса. Схема единственного деления
- Метод Гаусса — WiKi
Метод Гаусса (исключения неизвестных) — Мегаобучалка
Раздел 3. Численные методы решения уравнений
Виды математических моделей (уравнений) в теории электрических цепей
1. –системы линейных алгебраических уравнений –
линейные цепи постоянного и синусоидального переменного (комплексный метод) тока.
2. – системы нелинейных алгебраических или
трансцендентных уравнений – нелинейные цепи постоянного или синусоидального тока.
3. . –системы нелинейных дифференциальных
уравнений первого порядка в обыкновенных производных – переходные процессы в нелинейных цепях.
Здесь F и ψ – вектор-функции, т.е. эквивалентно записи:
f1(X,b1) = 0
f2(X,b2) = 0
…………
fn(X,bn) = 0
а –
ψ1(dX/dt,X,b1,t) = 0
ψ2(dX/dt,X,b2,t) = 0
…………………..
ψn(dX/dt,X,bn,t) = 0
Рассмотрим наиболее эффективные методы решения этих уравнений.
Численные методы решения систем линейных алгебраических уравнений (ЛАУ)
Метод Гаусса (исключения неизвестных)
Методы решения ЛАУ имеют важное значение, так как они применяются (итерационно) для решения более сложных уравнений.
Пусть система ЛАУ задана в виде:
,
,
где – квадратная матрица n – го порядка с ненулевыми диагональными элементами ; – вектор неизвестных; – вектор правых частей.
Алгоритм метода Гаусса состоит из прямогои обратного хода. Во время прямого хода осуществляется последовательное исключение неизвестных. Система приобретает вид:
Пересчет коэффициентов производится по формуле:
, где i, j = k+1, …n при исключение k-го неизвестного.
При этом столбец правых частей удобно рассматривать как n + 1 столбец матрицы коэффициентов , т.е. j = k+1, …n+1.
Обратный ход заключается в определении неизвестных, начиная с последнего уравнения где осталась одна неизвестная xn. Полученное значение xn подставляется в предыдущее уравнение и определяется xn-1 и т.д.
Для произвольного xk получается следующая формула:
где k = n, n -1,…1.
Трудоемкость метода Гаусса оценивается количеством выполняемых арифметических операций:
.
Кубическая зависимость от размерности задачи существенно ограничивает сложность анализируемых цепей. Однако если часть коэффициентов
Основная идея метода разреженных матриц состоит в учете при вычислениях и хранении только ненулевых элементов матрицы . Степень разреженности матрицы характеризуется коэффициентом заполнения:
;
где nннэ –число ненулевых элементов.
Существуют матрицы коэффициентов специального вида: ленточные, когда ненулевые элементы располагаются вдоль главной диагонали; и блочно-диагональные, когда вдоль главной диагонали располагаются ненулевые блоки. Еще встречаются блочно-диагональные с окаймлением.
Пример ленточной матрицы Пример блочно-диагональной матрицы
Пример блочно-диагональной матрицы с окаймлением
Для них разработаны специальные эффективные методы решения. Для диагональной – метод прогонки. Блочная распадается на отдельные группы уравнений по блокам, которые решаются методом Гаусса. Для блочно-диагональных с окаймлением существуют диакоптические методы решения.
Диакоптика – подход к исследованию сложных систем, заключающейся в расчленение системы на части и её анализе по частям при учете всех связей между выделенными частями.
megaobuchalka.ru
Метод последовательного исключения неизвестных. Метод Гаусса.
Идея метода основана на исключении
переменных до тех пор, пока не останется
только одна переменная в левой части
одного уравнения. Затем это уравнение
решается относительно этой единственной
переменной, и полученное значение
подставляется в предыдущее уравнение
для получения остающихся переменных.
Очевидно что предложенный алгоритм
работает, если а
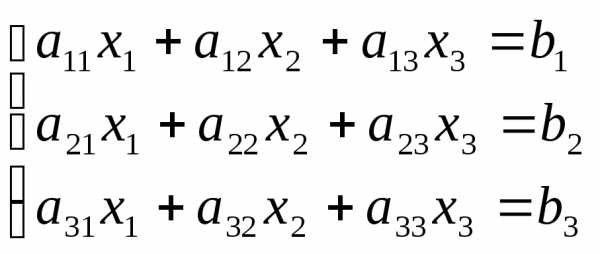 (6)
(6)
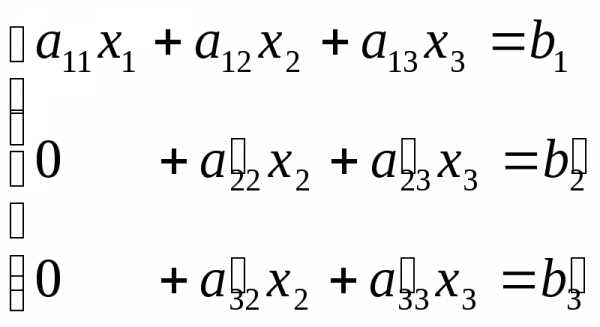 (7)
(7)
Второе уравнение системы (7) получено умножением первого уравнения этой системы на коэффициент −a21/a11 и сложением со вторым уравнением системы (6). Третье уравнение – путем умножения первого уравнения этой системы на коэффициент−a31/a11 и сложением с третьим уравнением системы (6).
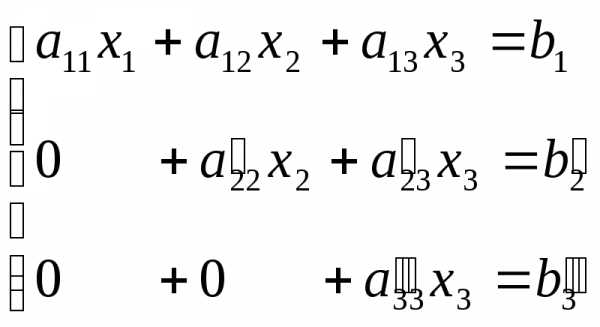 (8)
(8)
Третье уравнение системы (8) получено умножением второго уравнения системы (7) на коэффициент −a32
/a22 и сложением с третьим уравнением системы (6).Описанные этапы приводят к уравнению вида:
Ux=Mb,
где U– верхняя треугольная матрица. Диагональные элементы матрицы называются ведущими. K-ый ведущий элемент является коэффициентом при к-ой переменной в к-ом уравнении на к-ом шаге исключения.
Интуитивно можно утверждать, что к-ый элемент не должен быть слишком малым, иначе при делении будут получаться очень большие числа с большими абсолютными погрешностями. В результате этого решение может сильно исказиться.
Для того чтобы этого избежать применяются:
Масштабирование коэффициентов. Подход заключается в «отбрасывании» порядков при коэффициентах уравнений.
Метод Гаусса с выбором ведущего элемента. Отличие его от выше описанной схемы состоит в том что на к-ом шаге в качестве ведущего элемента берется наибольший по абсолютной величине элемент в неприведенной части к-ого столбца. Строка, содержащая этот элемент переставляется с к-ой строкой. Так же переставляются элементы правой части.
Гауссово исключение с выбором ведущих элементов гарантированно дает малые невязки. Связь между величинойошибки и невязкиотчасти определяетсячислом обусловленности.
Дополнительная информация приведена в Приложении 2.
Методы решения моделей по постоянному току. Линейный и нелинейный случаи (итерационные методы решения)
Идея итерации с неподвижной точкой.Большинство итерационных методов решения систем линейных и нелинейных уравнений могут быть рассмотрены как специальные случаи итерационного алгоритма с неподвижной точкой. Рассмотрим идею на примере уравнения с одним неизвестным
ƒ(х)=0. (9)
Алгоритм неподвижной точки требует специальной формы записиx=F(x) (10)
Целью алгоритма является нахождение x=x*, которое сводит уравнение (10) к тождеству. Преобразуем уравнение (10) к виду
Y=x Y= F(x). (11)
Тогда геометрическая интерпретация алгоритма будет выглядеть следующим образом (см. рис. 3)
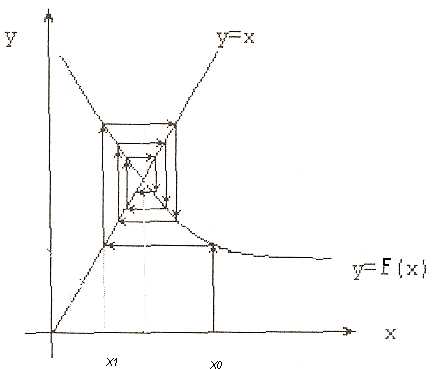
Рис. 3. Геометрическая интерпретация алгоритма неподвижной точки.
Предполагаем, что мы начинаем итерационную
процедуру выбрав х=х0,
в результате получаемх1
|xк+1–xк|<ε.(12)
В общем случае метод описывается рекурсивной формулой
xк+1=F(xк) (13)
Критерий, гарантирующий сходимость, определяется следующим образом (принцип сжатых отображений): если F(x)есть сжатиеn-мерного пространстваRnвRn, т.е. константаL<1, такая что
|| F(
y)-F(x)||<||y–x|| , х,у Є Rn , (14)то F(y) имеет единственную неподвижную точку.
Последовательные итерации приводят к этой неподвижной точке. Если Lблизка к единице, то сходимость может быть достаточно медленной.
Методы неподвижной точки требуют, чтобы
исходные уравнения 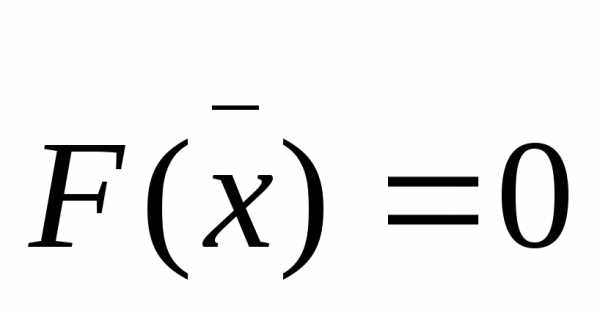 …
записывались в стандартной форме
…
записывались в стандартной форме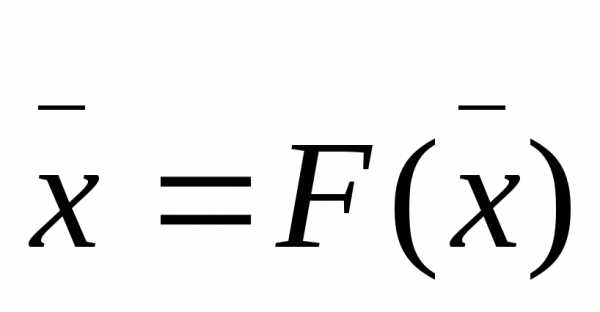 ,
где
,
где
, (15)
где 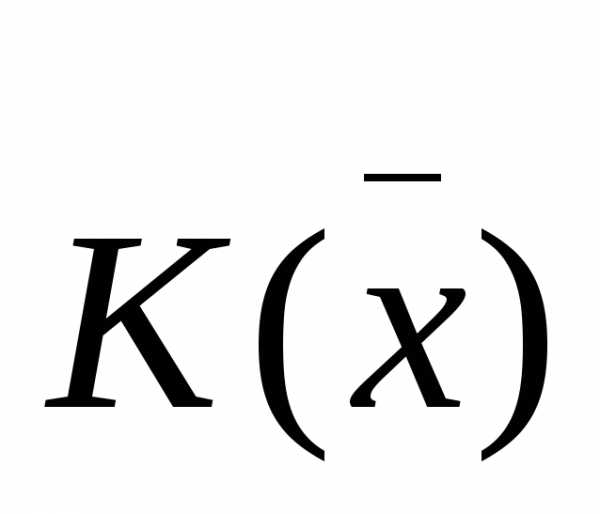 – матричная неособенная функция от
– матричная неособенная функция от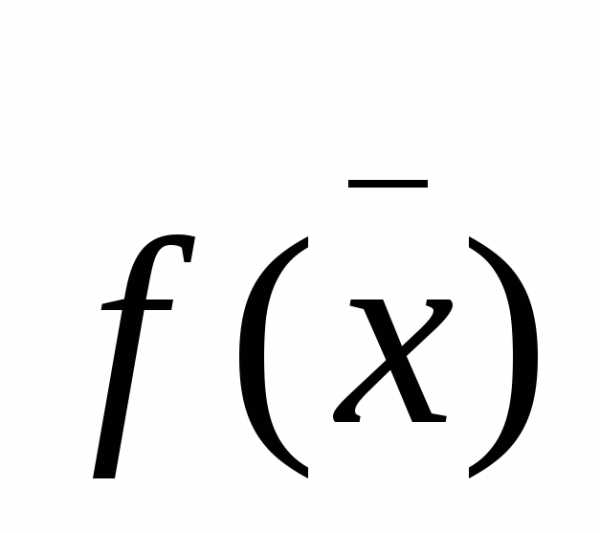 .
.
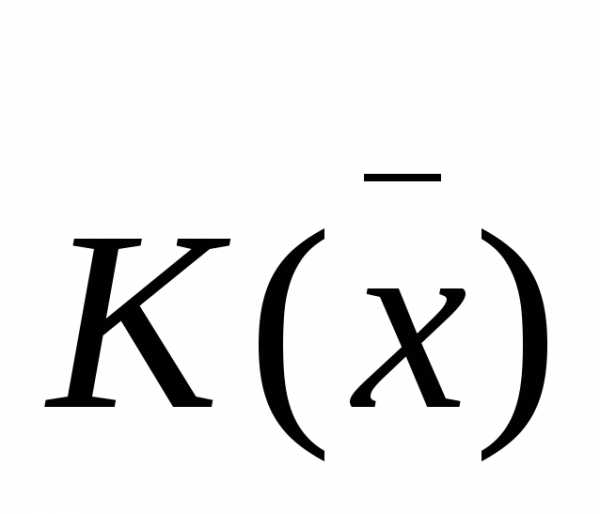 может быть случайной функцией. Различные
выборы
может быть случайной функцией. Различные
выборы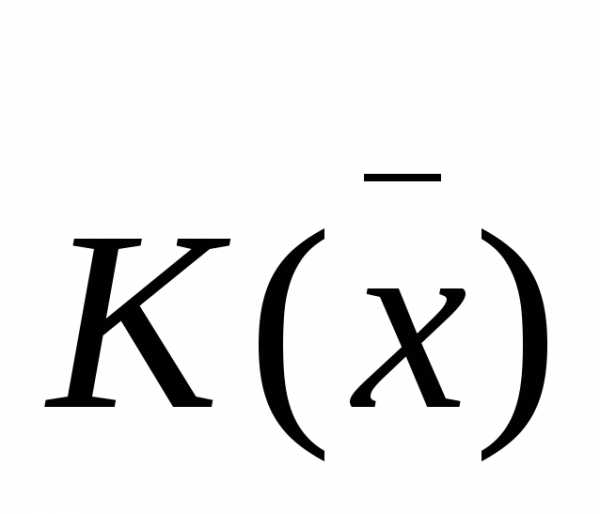 ведут к различным характеристикам
сходимости. Большинство итерационных
методов решения систем нелинейных
уравнений является специальными случаями
уравнения (15).
ведут к различным характеристикам
сходимости. Большинство итерационных
методов решения систем нелинейных
уравнений является специальными случаями
уравнения (15). Например,
,
где –
матрица Якоби.
–
матрица Якоби.
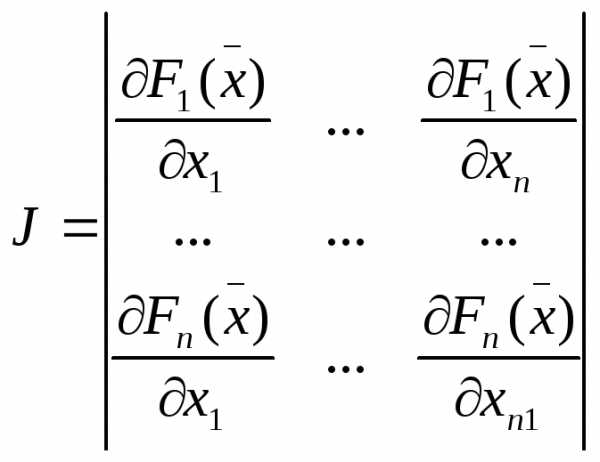
Подставляя в формулу (15), получим
. (16)
То есть приходим к методу Ньютона – Рафсона.
Метод Ньютона применяется на практике в большинстве случаев, поэтому остановимся на нем подробнее.
Известно, что всякую функцию в окрестности решения можно разложить в ряд Тейлора
(17)
При этом в окрестности решения можно ограничиться разложением с точностью до первого порядка малости. В методе Ньютона можно ввести преобразование, которое позволит сохранить невязку, если она мала, и уменьшить её, если она велика. Для метода Ньютона оправдывается теорема, если
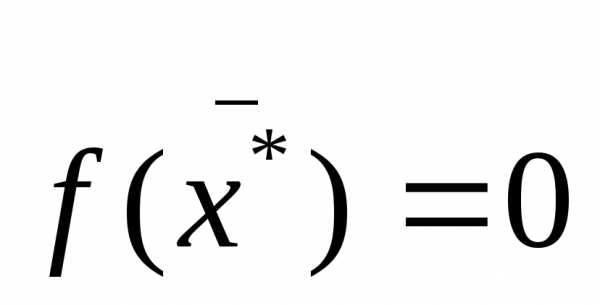 ,
,
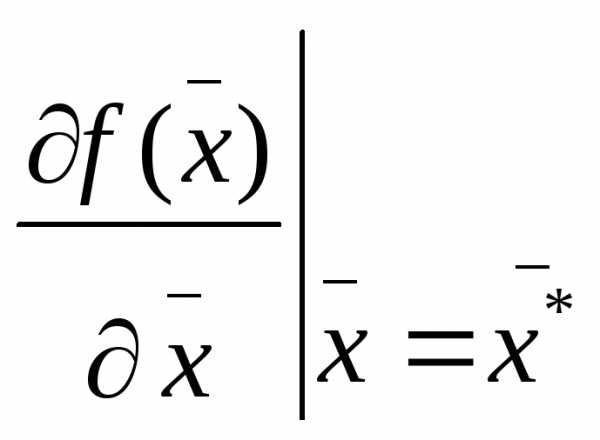 =0
=0
и вторая производная
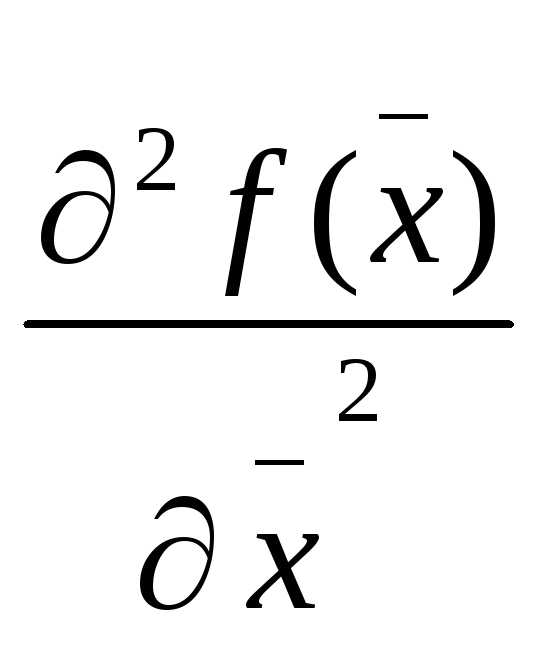
непрерывна, то существует открытый
интервал 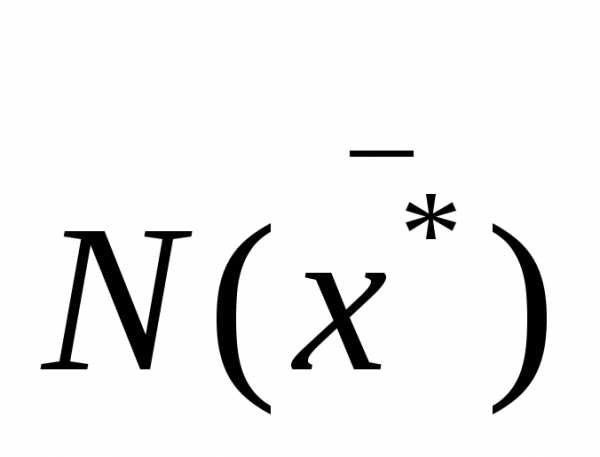 ,
содержащий
,
содержащий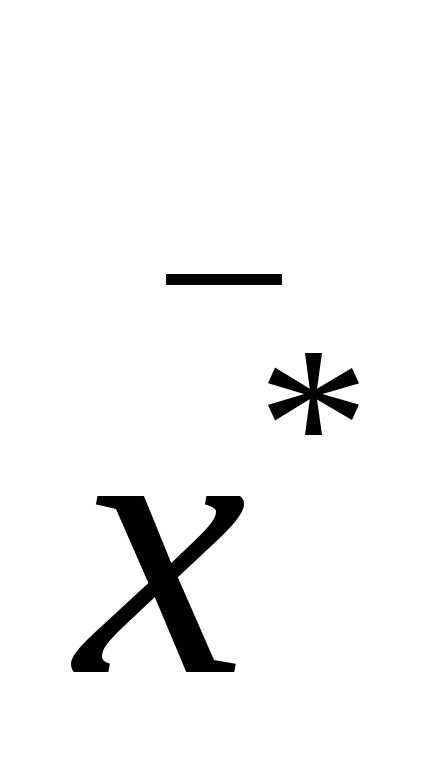 в решении, такой что, если
в решении, такой что, если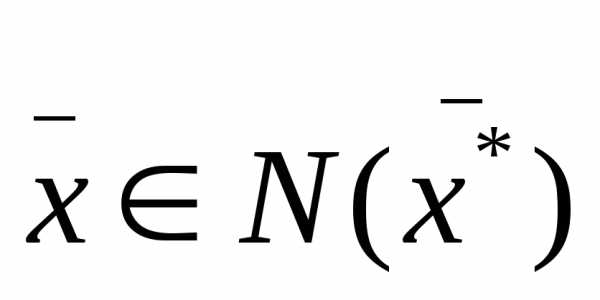 ,
то для метода Ньютона
,
то для метода Ньютона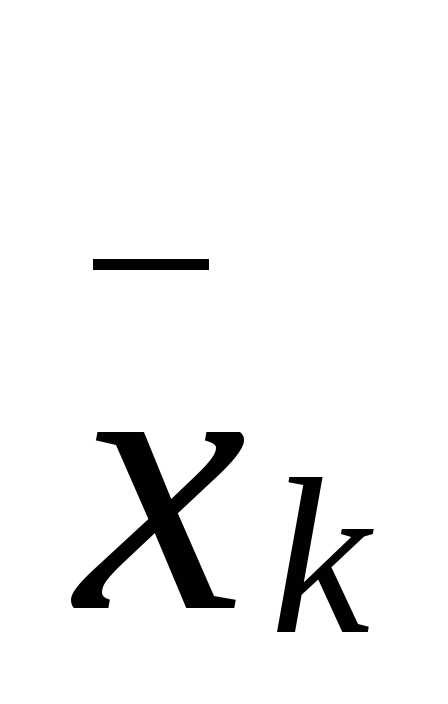 сходится к решению
сходится к решению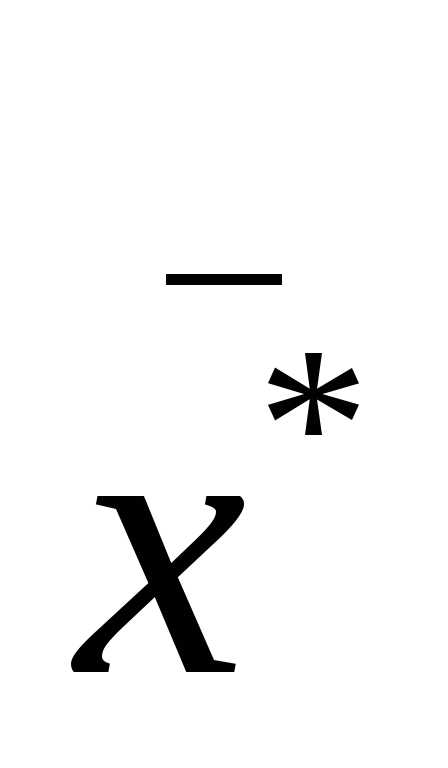 ,
т.е. метод Ньютона гарантирует сходимость
к решению при хорошем приближении.
,
т.е. метод Ньютона гарантирует сходимость
к решению при хорошем приближении.
Погрешность решения
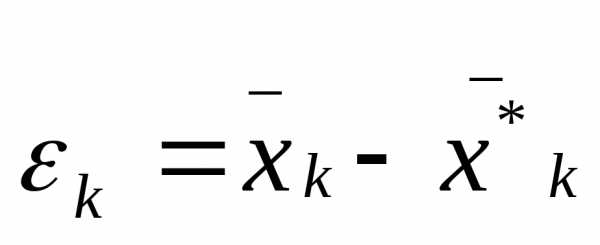 .
(18)
.
(18)
Нетрудно видеть, что
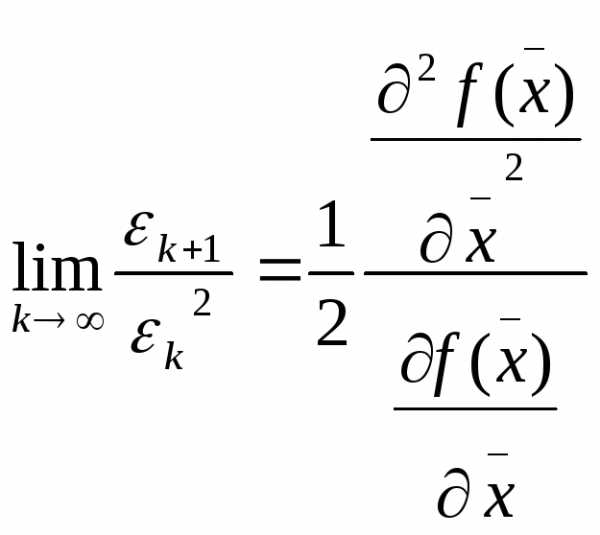 .
(19)
.
(19)
Если необходимо определить погрешность решения и сходимость, то нужно учесть второй порядок.
Об итерационном процессе, для которого
ошибка 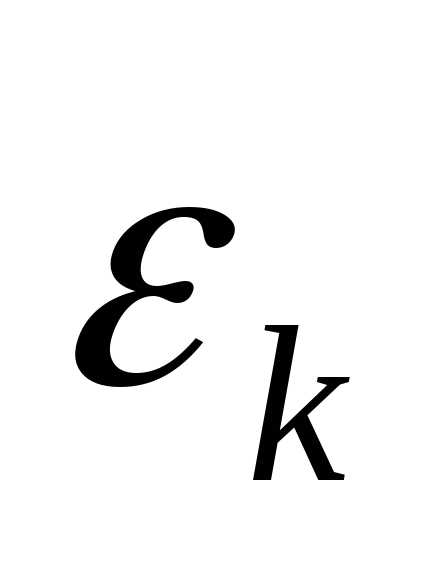 удовлетворяет соотношению
удовлетворяет соотношению
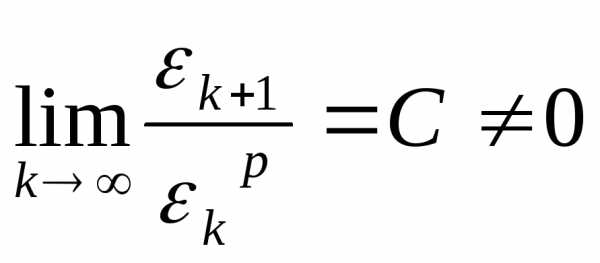 .
(20)
.
(20)
говорят, что он имеет сходимость порядка p, то есть метод Ньютона имеет квадратичную сходимость. Например, наk–ой итерации погрешность решения:
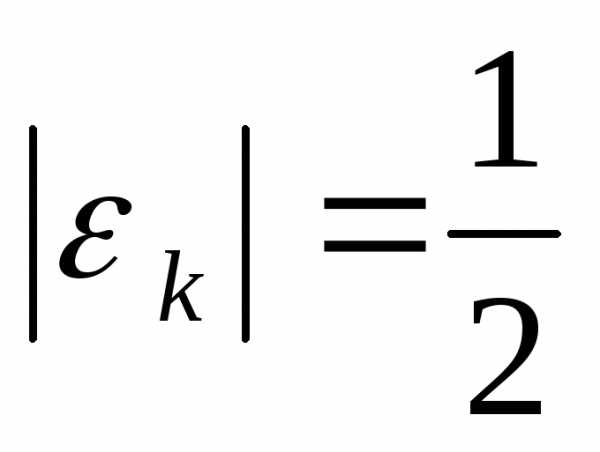 ,
,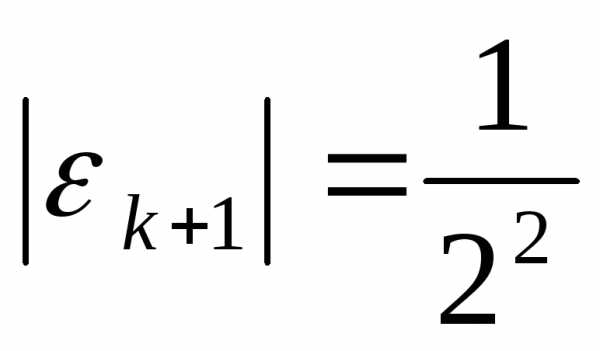 ,
,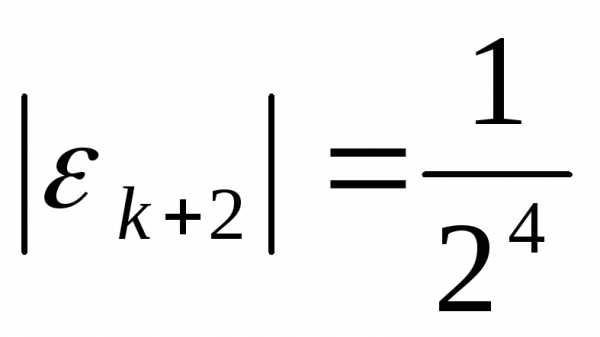 ,
,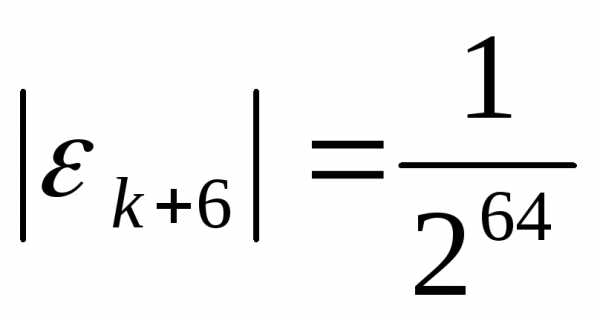 .
.
То есть, достаточно шести итераций для того, чтобы погрешность стала очень маленькой.
Трудность применения метода Ньютона
заключается в выборе начального
приближения, которое находилось бы
внутри интервала 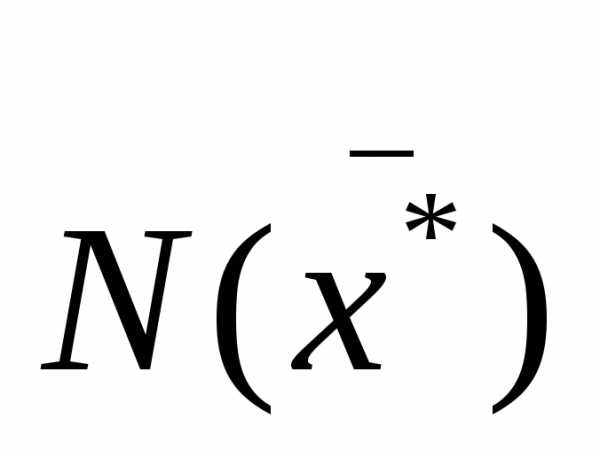 .
Если
.
Если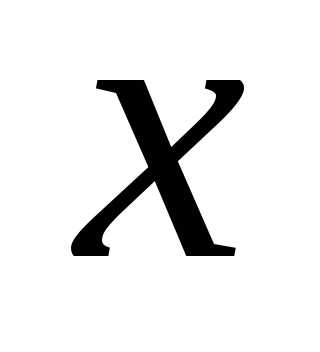 взят вне интервала (разложение в ряд
Тейлора в окрестности решения ), то нуль
не будет найден. Вследствие этого методу
Ньютона часто предшествует какой-либо
глобально сходящийся алгоритм (например,
метод деления отрезка пополам). То есть
метод Ньютона является завершающей
процедурой более медленных, но надежных
начальных алгоритмов.
взят вне интервала (разложение в ряд
Тейлора в окрестности решения ), то нуль
не будет найден. Вследствие этого методу
Ньютона часто предшествует какой-либо
глобально сходящийся алгоритм (например,
метод деления отрезка пополам). То есть
метод Ньютона является завершающей
процедурой более медленных, но надежных
начальных алгоритмов.
Локальная методическая погрешность
.
Различные подходы к выбору матрицы 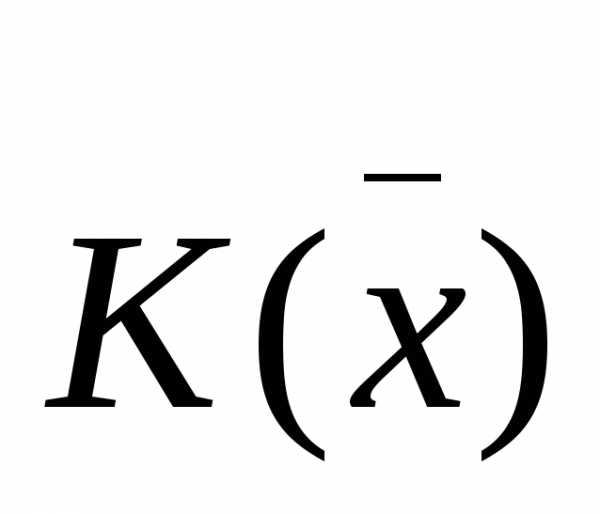 (помимо метода Ньютона) приводят к
методам Якоби, Гаусса–Зейделя, методу
последовательной верхней релаксации.
Перечисленные методы относятся к
релаксационным.
(помимо метода Ньютона) приводят к
методам Якоби, Гаусса–Зейделя, методу
последовательной верхней релаксации.
Перечисленные методы относятся к
релаксационным.
studfiles.net
1.6 Метод Гаусса (метод последовательного исключения неизвестных)
Большим недостатком двух рассмотренных методов (формулы Крамера и матричный метод) является их большая трудоемкость, связанная с громоздкими вычислениями при большом значении . Возможность применения этих методов ограничена также размерностью системы уравненийи требованием невырожденности матрицы системы.
Обойти эти сложности помогает универсальный метод решения СЛАУ – метод Гаусса, который еще называют методом последовательного исключения неизвестных.
Условно в методе Гаусса можно выделить 2 этапа: «прямой» и «обратный» ходы.
Прямой ход предполагает последовательное исключение неизвестных из уравнений системы, начиная с 1-го (движение сверху вниз).
Обратный ход – последовательное нахождение значений неизвестных, начиная с последнего уравнения системы (движение снизу вверх).
В основу метода Гаусса положены свойства равносильных (эквивалентных) систем (т.е. имеющих одни и те же решения).
Примем без доказательства тот факт, что система переходит в ей равносильную в результате элементарных преобразований, к которым относятся:
– перестановка уравнений местами;
– умножение всех членов уравнения на одно и то же число, отличное от нуля;
– прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на одно и то же число.
Таким образом, суть Метода Гаусса заключается в том, что с помощью элементарных преобразований СЛАУ приводится к равносильной системе ступенчатого вида, из которой затем последовательно находятся значения переменных, начиная с последнего уравнения.
Замечание. Преобразования по схеме Гаусса удобно проводить не с самими уравнениями, а с расширенной матрицей системы:
В этом случае элементарные преобразования производятся над строками. Тогда, прямой ход будет состоять в получении нулей под главной диагональю. Затем по расширенной матрице восстанавливают систему и обратным ходом последовательно находят значения переменных.
Алгоритм Метода Гаусса цикличен, т.е. одна и та же операция будет по очереди повторяться для каждой неизвестной. Условно его можно выразить фразой: «диагональный элемент не ноль, под ним нули».
Рассмотрим СЛАУ (случай ):
(6.1)
Пусть (еслито перестановкой уравнений местами добьемся, чтобы выполнялось условие. Это приведет к равносильной системе уравнений). Разделим 1-е уравнение системы на. Оно примет вид:
где
ШАГ 1. Умножая это уравнение последовательно на и прибавляя полученные уравнения в том же порядке ко 2-му, 3-му … -му уравнениям, исключим переменную из всех уравнений системы, начиная со второго.
Получим:
(6.2)
ШАГ 2. Пусть (если это не так, то перестановкой уравнений или неизвестных с изменением их номеров добьемся, чтобы выполнялось условие).
Разделим второе уравнение системы на . Это уравнение примет вид
где
Умножая полученное уравнение последовательно на и прибавляя полученные уравнения в том же порядке к третьему … -му уравнению системы, исключим переменнуюиз всех уравнений системы, начиная с третьего.
Продолжая процесс последовательного исключения переменных после-го шага получим систему вида
(6.3)
Число нуль в последних уравнениях означает, что их левые части имеют вид . Если в полученной системе уравнений хотя бы одно из чиселне равно нулю, то соответствующее равенство противоречиво, и система (6.1) несовместна.
Для любой совместной системы (6.1) числа в системе (6.3) равны нулю. В этом случае последниеуравнений являются тождествами и их можно исключить при решении системы (6.3). После исключения из системы (6.3) последнихуравнений возможны два случая: 1) число уравнений, оставшихся в системе (6.3), равно числу неизвестных, т.е., тогда система (6.3) имеет треугольный вид и решение системы (6.1) единственное; 2)(тогда система (6.3) имеет ступенчатый вид и система (6.1) неопределенная, имеет бесчисленное множество решений).
Пример 1. Решить систему уравнений методом Гаусса:
Составим расширенную матрицу системы
Разделим первую строку матрицы на 2.
ШАГ 1.
ШАГ 2.
Разделим вторую строку полученной матрицы на
ШАГ 3.
Разделим третью строку на
Прямой ход на этом окончен.
Последней матрице соответствует система уравнений:
Обратный ход: из третьего уравнения системы
из второго уравнения системы
из первого уравнения системы
Ответ:
Пример 2. Методом Гаусса решить систему уравнений:
Запишем и преобразуем расширенную матрицу системы
Уравнение, соответствующее третьей строке полученной матрицы, представляет равенство . Следовательно, система несовместна.
Ответ: решений нет.
Замечания:
Кроме решения СЛАУ методом Гаусса можно вычислять определители. После выполнения прямого хода определитель равен произведению элементов, стоящих на главной диагонали.
Метод Гаусса помогает также находить обратную матрицу через присоединенную: к исходной матрицеприписывается рядом единичная; затем проводятся элементарные преобразования, приводящие матрицук виду единичной, при этом единичная матрица приводится к обратной
При решении СЛАУ методом Гаусса одновременно осуществляется исследование системы.
studfiles.net
Тема 3 Метод последовательного исключения неизвестных (метод Гаусса)
Поиск ЛекцийМетод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Рассмотрим метод Гаусса на примере системы из трёх уравнений с тремя неизвестными:
Первое уравнение оставим без изменения, а из второго и третьего исключим слагаемые, содержащие . Для этого второе уравнение разделим на и умножим на , а затем сложим с первым уравнением. Аналогично третье уравнение разделим на и умножим на и сложим с первым. В результате исходная система примет вид:
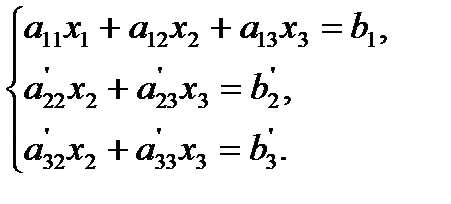
Теперь из последнего уравнения легко найти , затем из второго уравнения . Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:
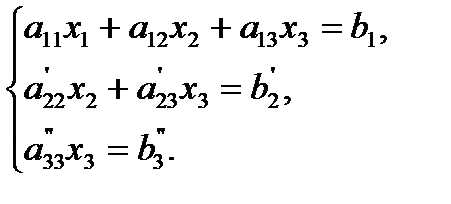
Отсюда легко найти , затем из второго уравнения , и из первого . Вместо того чтобы писать систему уравнений выписывают расширенную матрицу системы, которая состоит из коэффициентов этой системы и свободных членов. Приводим ее к ступенчатому виду.
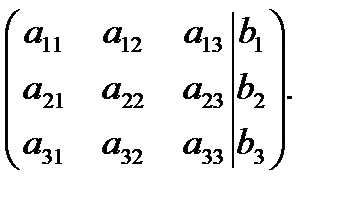
Матрица имеет ступенчатый вид, если
· все ненулевые строки (имеющие по крайней мере один ненулевой элемент) располагаются над всеми чисто нулевыми строками;
· ведущий элемент (первый ненулевой элемент строки при отсчёте слева направо) каждой ненулевой строки располагается строго правее ведущего элемента в строке, расположенной выше данной.
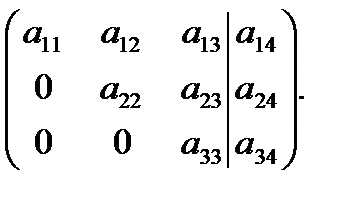
Цель элементарных преобразований– привести матрицу к ступенчатому (треугольному) виду.
Элементарными преобразованиями матрицы называются следующие ее преобразования:
I Перестановка двух строк матрицы.
II Умножение всех элементов одной строки матрицы на одно и то же число, отличное от нуля.
III Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на одно и то же число.
IV Вычеркивание нулевой строки.
Пример:
Решить методом Гаусса систему уравнений:
Запишем расширенную матрицу системы: 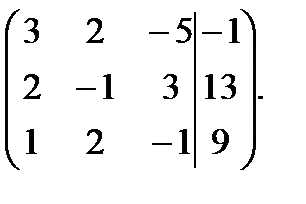
Поменяем местами первую и третью строки
Мы получили единицу в верхнем углу. Теперь нужно получить нули в первом столбце 2-ой и 3-ей строки. Для этого ко второй строке прибавим первую строку, умноженную на -2:
К третьей строке прибавим первую, умноженную на 3:
Вторую строку умножим на -1/5, а третью строку на -1/2
К третьей строке прибавим вторую строку, умноженную на -2
Из последней строчки находим, что .
Из второй строки находим y:
И из первой строки найдем x:
Таким образом, мы нашли решение системы:
Решить методом Гаусса следующие системы уравнений:
1 2 3 4
5 6 7 8 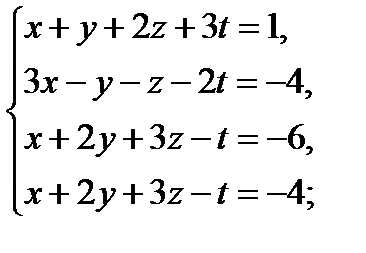
9 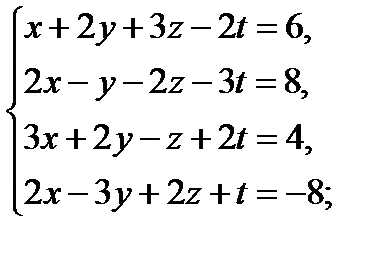 10
10 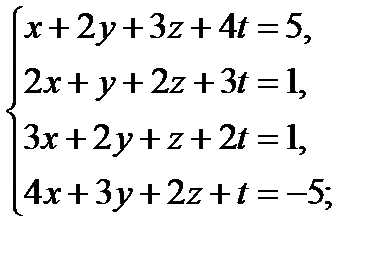 11
11 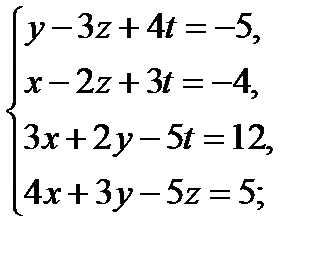
12 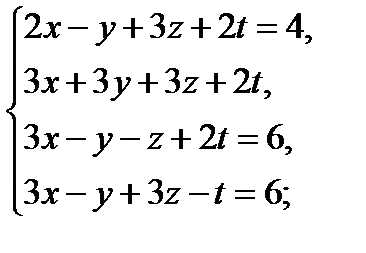 13
13 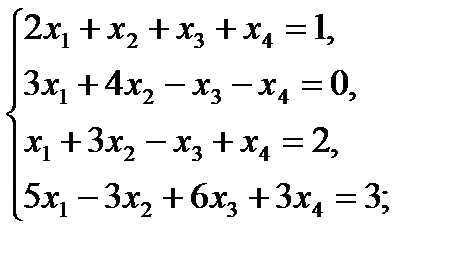 14
14 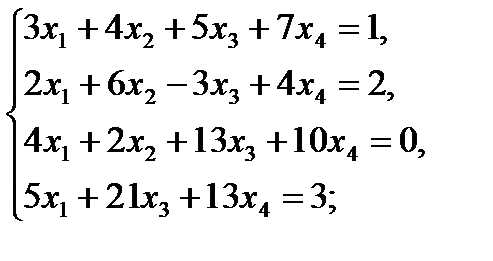
15 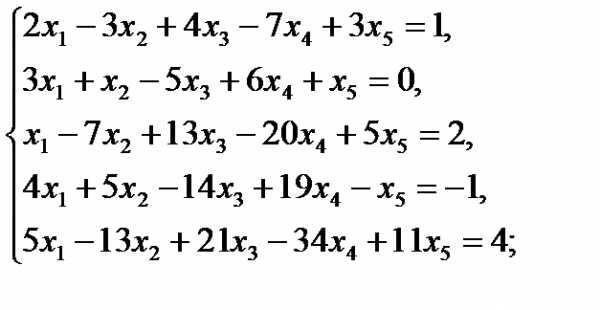 16
16 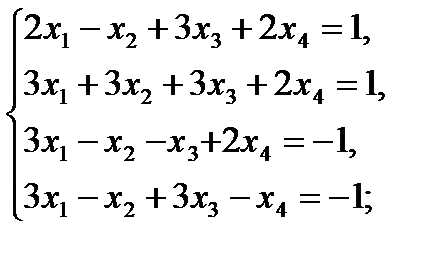
17 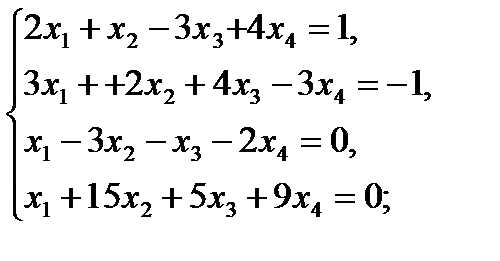 18
18 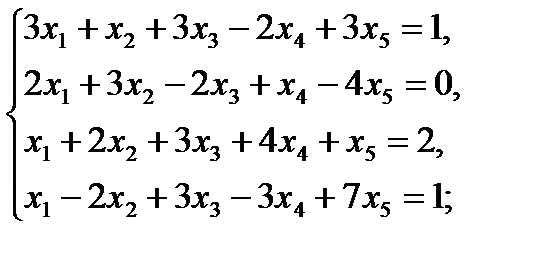
19 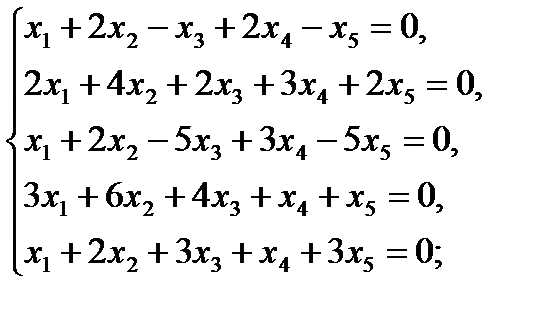 20
20 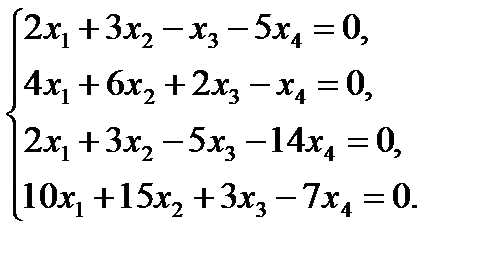
Шатных Олеся Николаевна
АЛГЕБРА
(ЧАСТЬ 1)
Материалы для практических занятий
и самостоятельной работы
для студентов факультета М и ИТ
Редактор
____________________________________________________________________
Подписано к печати Формат бумаги 60 84 1/16 Бумага тип № 1
Печать цифровая Усл. печ.л. 2,25 Уч.-изд.л.
Заказ Тираж 30 Не для продажи
____________________________________________________________________
РИЦ Курганского государственного университета.
640669, г. Курган, ул. Гоголя, 25.
Курганский государственный университет.
poisk-ru.ru
Метод Гаусса. Метод последовательного исключения неизвестных
⇐ ПредыдущаяСтр 18 из 18Историческая справка
Метод Гаусса был предложен известнейшим немецким математиком Карлом Фридрихом Гауссом (1777 – 1855) и является одним из наиболее универсальных методов решения СЛАУ. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении задачи, расширенная матрица системы с помощью элементарных преобразований над ее строками приводится к ступенчатому виду. Далее последовательно находятся все неизвестные, начиная снизу вверх.
Принцип метода Гаусса
Метод Гаусса включает в себя прямой (приведение расширенной матрицы к ступенчатому виду, то есть получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и называется методом Гаусса, обратный – методом Гаусса-Жордана, который отличается от первого только последовательностью исключения переменных.
Метод Гаусса идеально подходит для решения систем содержащих больше трех линейных уравнений, для решения систем уравнений, которые не являются квадратными (чего не скажешь про метод Крамера и матричный метод). То есть метод Гаусса – наиболее универсальный метод для нахождения решения любой системы линейных уравнений, он работает в случае, когда система имеет бесконечно много решений или несовместна.
Примеры решения систем уравнений
Пример
Задание. Решить СЛАУ методом Гаусса.
Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент равнялся 1 (это мы делаем для упрощения вычислений):
Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей – три первых:
Все элементы третьей строки делим на два (или, что тоже самое, умножаем на ):
Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:
От третьей строки отнимаем вторую, умноженную на 3:
Умножив третью строку на , получаем:
Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент , для этого от второй строки отнимем третью:
Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:
Полученной матрице соответствует система
или
Ответ.
mykonspekts.ru
3.2 Метод исключения Гаусса. Схема единственного деления
Основная идея метода исключений Гаусса состоит в том, что система уравнений (3.1) приводится к эквивалентной ей системе с верхней треугольной матрицей (прямой ход исключений), а затем неизвестные вычисляются последовательной подстановкой (обратный ход исключений).
Рассмотрим сначала простейший метод исключения Гаусса, называемый схемой единственного деления.
Прямой ход состоит из n – 1 шагов. На первом шаге исключается переменная x1 из всех уравнений, кроме первого. Для этого нужно из второго, третьего, …, n-го уравнений вычесть первое, умноженное на величину
m = , i = 2, 3, …, n. (3.4)
При этом коэффициенты при x1 обратятся в нуль во всех уравнениях, кроме первого.
Введем обозначения:
a = aij – ma1j , b= bi – mb1. (3.5)
Легко убедиться, что для всех уравнений, начиная со второго, a= 0, i = 2, 3, …, n. Преобразованная система запишется в виде:
a11x1 + a12 x2 + a13x3 + … + a1nxn = b1
ax2 + ax3 + … + axn = b
a x2 + ax3 + … + axn = b (3.6)
ax2 + ax3 + … + axn = b
Все уравнения (3.6), кроме первого, образуют систему (n – 1)-го порядка. Применяя к ней ту же процедуру, мы можем исключить из третьего, четвертого, …, n-го уравнений переменную x2. Точно так же исключаем переменную x3 из последних n – 3 уравнений.
На некотором k-ом шаге в предположении, что главный элемент k-ого шага a0, переменная xk исключается с помощью формул:
m = ,
a = a – ma ,
b= b – mb, i, j = k + 1, k + 2, …, n. (3.7)
Индекс k принимает значения 1, 2, …, n – 1.
При k = n – 1 получим треугольную систему:
a11x1 + a12 x2 + a13x3 + … + a1nxn = b1
ax2 + ax3 + …+ axn = b
ax3 + …+ axn = b (3.8)
axn = b
с треугольной матрицей An.
Приведение системы (3.1) к треугольному виду (3.8) составляет прямой ход метода Гаусса.
При использовании метода Гаусса нет необходимости в предварительном обосновании существования и единственности решения (т. е. доказательства, что det A 0). Если на k-ом шаге все элементы a (i = k, k + 1, …, n) окажутся равными нулю, то система (3.1) не имеет единственного решения.
Обратный ход состоит в вычислении переменных. Из последнего уравнения (3.8) определяем xn... Подставляя его в предпоследнее уравнение, находим xn-1, и т. д. Общие формулы имеют вид:
xn = ,
xk = (b- a xk+1– a xk+2 – … – a xn), k = n – 1, n – 2, …, 1 (3.9)
Трудоемкость метода. Для реализации метода исключения Гаусса требуется примерно 2/3n3 операций для прямого хода и n2 операций для обратного хода. Таким образом, общее количество операций составляет примерно 2/3n3 + n2.
Пример 3.1.
Применим метод исключения Гаусса по схеме единственного деления для решения системы уравнений:
2.0x1 + 1.0x2 – 0.1x3 + 1.0x4 = 2.7
0.4x1 + 0.5x2 + 4.0x3 – 8.5x4 = 21.9
0.3x1 – 1.0x2 + 1.0x3 + 5.2x4 = – 3.9 (3.10)
1.0x1 + 0.2x2 + 2.5x3 – 1.0x4 = 9.9
Будем делать округление чисел до четырех знаков после десятичной точки.
Прямой ход. 1-ый шаг. Вычислим множители:
m = = = 0.2; m = = = 0.15; m = = = 0.5.
Вычитая из второго, третьего и четвертого уравнений системы (3.10) первое уравнение, умноженное соответственно на m, m, m, получим новую систему:
2.0x1 + 1.0x2 – 0.1x3 + 1.0x4 = 2.7
0.3x2 + 4.02x3 – 8.70x4 = 21.36
-1.15x2 + 1.015x3 + 5.05x4 = – 4.305 (3. 11)
– 0.30x2 + 2.55x3 – 1.50x4 = 8.55
2-ой шаг. Вычислим множители:
m = = = – 3.83333; m = = = -1.0.
Вычитая из третьего и четвертого уравнений системы (3.11) второе уравнение, умноженное соответственно на m и m, приходим к системе:
2.0x1 + 1.0x2 – 0.1x3 + 1.0x4 = 2.7
0.3x2 + 4.02x3 – 8.70x4 = 21.36
16. 425x3 – 28.300x4 = 77.575 (3.12)
6.570x3 – 10.200x4 = 29.910
3-ий шаг. Вычислим множитель:
m = = = 0.4.
Вычитая из четвертого уравнения системы (3.12) третье, умноженное на m, приведем систему к треугольному виду:
2.0x1 + 1.0x2 – 0.1x3 + 1.0x4 = 2.7
0.3x2 + 4.02x3 – 8.70x4 = 21.36
16. 425x3 – 28.300x4 = 77.575 (3.13)
1.12x4 = -1.12
Обратный ход. Из последнего уравнения системы (3.13) находим x4 = 1.000. Подставляя значение x4 в третье уравнение, получим x3 = 2.000. Подставляя найденные значения x4 и x3 во второе уравнение, найдем x2 = 3.000. Наконец, из первого уравнения, подставив в него найденные значения x4, x3 и x2, вычислим x1 = -1.000.
Итак система (3.10) имеет следующее решение:
x1 = 1.000, x2 = 2.000, x3 = 3.000, x4 = – 1.000.
studfiles.net
Метод Гаусса — WiKi
Пусть исходная система выглядит следующим образом:
- {a11x1+…+a1nxn=b1…am1x1+…+amnxn=bm{\displaystyle \left\{{\begin{array}{lcr}a_{11}x_{1}+\ldots +a_{1n}x_{n}&=&b_{1}\\\ldots &&\\a_{m1}x_{1}+\ldots +a_{mn}x_{n}&=&b_{m}\\\end{array}}\right.}
Её можно записать в матричном виде:
- Ax=b,{\displaystyle Ax=b,}
где
- A=(a11…a1n…am1…amn),x=(x1⋮xn),b=(b1⋮bm).(1){\displaystyle A=\left({\begin{array}{ccc}a_{11}&\ldots &a_{1n}\\\ldots &&\\a_{m1}&\ldots &a_{mn}\end{array}}\right),\quad x=\left({\begin{array}{c}x_{1}\\\vdots \\x_{n}\end{array}}\right),\quad b=\left({\begin{array}{c}b_{1}\\\vdots \\b_{m}\end{array}}\right).\quad (1)}
Матрица A{\displaystyle A} называется основной матрицей системы, b{\displaystyle b} — столбцом свободных членов.
Тогда, согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):
- {α1j1xj1+α1j2xj2+…+α1jrxjr+…+α1jnxjn=β1α2j2xj2+…+α2jrxjr+…+α2jnxjn=β2…αrjrxjr+…+αrjnxjn=βr0=βr+1…0=βm,{\displaystyle \left\{{\begin{array}{rcl}\alpha _{1j_{1}}x_{j_{1}}+\alpha _{1j_{2}}x_{j_{2}}+\ldots +\alpha _{1j_{r}}x_{j_{r}}+\ldots +\alpha _{1j_{n}}x_{j_{n}}&=&\beta _{1}\\\alpha _{2j_{2}}x_{j_{2}}+\ldots +\alpha _{2j_{r}}x_{j_{r}}+\ldots +\alpha _{2j_{n}}x_{j_{n}}&=&\beta _{2}\\&\ldots &\\\alpha _{rj_{r}}x_{j_{r}}+\ldots +\alpha _{rj_{n}}x_{j_{n}}&=&\beta _{r}\\0&=&\beta _{r+1}\\&\ldots &\\0&=&\beta _{m}\end{array}}\right.,}
где α1j1,…,αrjr≠0.{\displaystyle \alpha _{1j_{1}},\ldots ,\alpha _{rj_{r}}\neq 0.}
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных xj1,…,xjr{\displaystyle x_{j_{1}},\ldots ,x_{j_{r}}} [3].
Тогда переменные xj1,…,xjr{\displaystyle x_{j_{1}},\ldots ,x_{j_{r}}} называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число βi≠0{\displaystyle \beta _{i}\neq 0} , где i>r{\displaystyle i>r} , то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.
Пусть βi=0{\displaystyle \beta _{i}=0} для любых i>r{\displaystyle i>r} .
Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом x{\displaystyle x} (αiji,i=1,…,r{\displaystyle \alpha _{ij_{i}},\,i=1,\ldots ,r} , где i{\displaystyle i} — номер строки):
- {xj1+α^1j2xj2+…+α^1jrxjr=β^1−α^1jr+1xjr+1−…−α^1jnxjnxj2+…+α^2jrxjr=β^2−α^2jr+1xjr+1−…−α^2jnxjn…xjr=β^r−α^rjr+1xjr+1−…−α^rjnxjn,β^i=βiαiji,α^ijk=αijkαiji(2){\displaystyle \left\{{\begin{array}{rcc}x_{j_{1}}+{\widehat {\alpha }}_{1j_{2}}x_{j_{2}}+\ldots +{\widehat {\alpha }}_{1j_{r}}x_{j_{r}}&=&{\widehat {\beta }}_{1}-{\widehat {\alpha }}_{1j_{r+1}}x_{j_{r+1}}-\ldots -{\widehat {\alpha }}_{1j_{n}}x_{j_{n}}\\x_{j_{2}}+\ldots +{\widehat {\alpha }}_{2j_{r}}x_{j_{r}}&=&{\widehat {\beta }}_{2}-{\widehat {\alpha }}_{2j_{r+1}}x_{j_{r+1}}-\ldots -{\widehat {\alpha }}_{2j_{n}}x_{j_{n}}\\&\ldots &\\x_{j_{r}}&=&{\widehat {\beta }}_{r}-{\widehat {\alpha }}_{rj_{r+1}}x_{j_{r+1}}-\ldots -{\widehat {\alpha }}_{rj_{n}}x_{j_{n}}\\\end{array}}\right.,\qquad {\widehat {\beta }}_{i}={\frac {\beta _{i}}{\alpha _{ij_{i}}}},\quad {\widehat {\alpha }}_{ij_{k}}={\frac {\alpha _{ij_{k}}}{\alpha _{ij_{i}}}}\quad (2)} ,
где i=1,…,r,k=i+1,…,n.{\displaystyle i=1,\ldots ,r,\quad k=i+1,\ldots ,n.}
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
| Следствия: 1: Если в совместной системе все переменные главные, то такая система является определённой. 2: Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной. |
Критерий совместности
Упомянутое выше условие βi=0{\displaystyle \beta _{i}=0} для всех i>r{\displaystyle i>r} может быть сформулировано в качестве необходимого и достаточного условия совместности:
Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны).
| Теорема Кронекера — Капелли. Система совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. Следствия:
|
Алгоритм
Блок схема представлена на рисунке. Данный рисунок адаптированный для написания программы на языке С/С++, где a[0] столбец свободных членов.
Алгоритм Гаусса для решения СЛАУОписание
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.
- На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
- На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Метод Гаусса требует O(n3){\displaystyle O(n^{3})} арифметических операций.
Этот метод опирается на:
| Теорема (о приведении матриц к ступенчатому виду). Любую матрицу путём элементарных преобразований только над строками можно привести к ступенчатому виду. |
Простейший случай
В простейшем случае алгоритм выглядит так:
- {a11⋅x1+a12⋅x2+…+a1n⋅xn=b1(1)a21⋅x1+a22⋅x2+…+a2n⋅xn=b2(2)…am1⋅x1+am2⋅x2+…+amn⋅xn=bm(m){\displaystyle \left\{{\begin{array}{lcc}a_{11}\cdot x_{1}+a_{12}\cdot x_{2}+\ldots +a_{1n}\cdot x_{n}&=b_{1}&(1)\\a_{21}\cdot x_{1}+a_{22}\cdot x_{2}+\ldots +a_{2n}\cdot x_{n}&=b_{2}&(2)\\\ldots &&\\a_{m1}\cdot x_{1}+a_{m2}\cdot x_{2}+\ldots +a_{mn}\cdot x_{n}&=b_{m}&(m)\end{array}}\right.}
- (2)→(2)−(1)⋅(a21a11):a22′⋅x2+a23′⋅x3+…+a2n′⋅xn=b2′(3)→(3)−(1)⋅(a31a11):a32′⋅x2+a33′⋅x3+…+a3n′⋅xn=b3′…(m)→(m)−(1)⋅(am1a11):am2′⋅x2+am3′⋅x3+…+amn′⋅xn=bn′(3)→(3)−(2)⋅(a32′a22′):a33′′⋅x3+…+a3n′′⋅xn=b3′′…(m)→(m)−(m−1)⋅(am,n−1(m−2)am−1,n−1(m−2)):amm(m−1)⋅xm+…+amn(m−1)⋅xn=bm(m−1){\displaystyle {\begin{array}{ccc}(2)\to (2)-(1)\cdot ({\frac {a_{21}}{a_{11}}})&:&a_{22}^{\prime }\cdot x_{2}+a_{23}^{\prime }\cdot x_{3}+\ldots +a_{2n}^{\prime }\cdot x_{n}=b_{2}^{\prime }\\(3)\to (3)-(1)\cdot ({\frac {a_{31}}{a_{11}}})&:&a_{32}^{\prime }\cdot x_{2}+a_{33}^{\prime }\cdot x_{3}+\ldots +a_{3n}^{\prime }\cdot x_{n}=b_{3}^{\prime }\\\ldots &&\\(m)\to (m)-(1)\cdot ({\frac {a_{m1}}{a_{11}}})&:&a_{m2}^{\prime }\cdot x_{2}+a_{m3}^{\prime }\cdot x_{3}+\ldots +a_{mn}^{\prime }\cdot x_{n}=b_{n}^{\prime }\\(3)\to (3)-(2)\cdot ({\frac {a_{32}^{\prime }}{a_{22}^{\prime }}})&:&a_{33}^{\prime \prime }\cdot x_{3}+\ldots +a_{3n}^{\prime \prime }\cdot x_{n}=b_{3}^{\prime \prime }\\\ldots &&\\(m)\to (m)-(m-1)\cdot ({\frac {a_{m,n-1}^{(m-2)}}{a_{m-1,n-1}^{(m-2)}}})&:&a_{mm}^{(m-1)}\cdot x_{m}+\ldots +a_{mn}^{(m-1)}\cdot x_{n}=b_{m}^{(m-1)}\end{array}}}
- Обратный ход. Из последнего ненулевого уравнения выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения. Повторяя эту процедуру для всех базисных переменных, получаем фундаментальное решение.
Пример
Покажем, как методом Гаусса можно решить следующую систему:
- {2x+y−z=8−3x−y+2z=−11−2x+y+2z=−3{\displaystyle \left\{{\begin{array}{ccc}2x+y-z&=&8\\-3x-y+2z&=&-11\\-2x+y+2z&=&-3\end{array}}\right.}
Обнулим коэффициенты при x{\displaystyle x} во второй и третьей строчках. Для этого прибавим к ним первую строчку, умноженную на 32{\displaystyle \textstyle {\frac {3}{2}}} и 1{\displaystyle 1} , соответственно:
- {2x+y−z=812y+12z=12y+z=5{\displaystyle \left\{{\begin{array}{rcc}2x+y-z&=&8\\{\frac {1}{2}}y+{\frac {1}{2}}z&=&1\\2y+z&=&5\end{array}}\right.}
Теперь обнулим коэффициент при y{\displaystyle y} в третьей строке, вычтя из неё вторую строку, умноженную на 4{\displaystyle 4} :
- {2x+y−z=812y+12z=1−z=1{\displaystyle \left\{{\begin{array}{rcc}2x+y-z&=&8\\{\frac {1}{2}}y+{\frac {1}{2}}z&=&1\\-z&=&1\\\end{array}}\right.}
В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
- z=−1{\displaystyle z=-1} из третьего;
- y=3{\displaystyle y=3} из второго, подставив полученное z{\displaystyle z}
- x=2{\displaystyle x=2} из первого, подставив полученные z{\displaystyle z} и y{\displaystyle y} .
Таким образом исходная система решена.
В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.
ru-wiki.org



