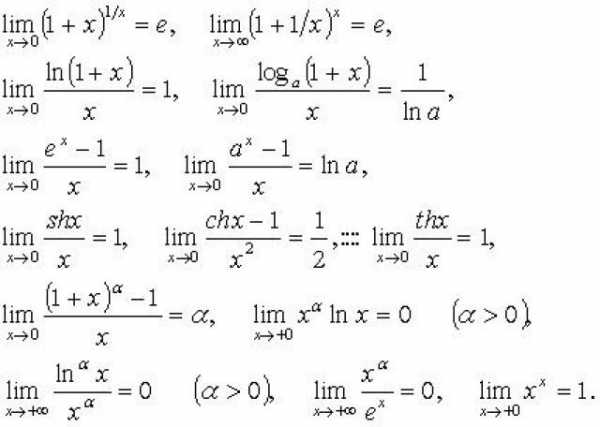Предел равен – Калькулятор онлайн - Решение пределов - Центр социальной реабилитации инвалидов и детей-инвалидов Фрунзенского района Санкт-Петербурга

14.06.201926.12.2018

Предел равен – Калькулятор онлайн – Решение пределов

Содержание

Предел постоянной величины – Предел постоянной величины равен самой постоянной величине — КиберПедия

Предел переменной величины

Предел — постоянная, к которой неограниченно приближается некоторая переменная величина, зависящая от другой переменной величины, при определённом изменении последней. Простейшим является понятие Предел числовой последовательности, с помощью которого могут быть определены понятия Предел функции, Предел последовательности точек пространства, Предел интегральных сумм.

Основные свойства пределов

Предел постоянной величины – Предел постоянной величины равен самой постоянной величине

Предел суммы – Предел суммы двух функций равен сумме пределов этих функций

Предел произведения функции на постоянную величину – Постоянный коэффициэнт можно выносить за знак предела

Предел произведения – Предел произведения двух функций равен произведению пределов этих функций.

Предел частного – Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю

Пределы на бесконечности

Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим. Существуют различные определения таких пределов, но они эквивалентны между собой.

Приращение аргумента и приращение функции

Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

Определение производной

Произво?дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци?рованием. Обратный процесс — интегрирование.

Правила дифференцирования алгебраической суммы

Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

(u±v)’ = u’±v’

Следствие. Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например, (u — v + w)’ = u’ — v’ + w’.

Правила дифференцирования произведений

Правило произведения — характерное свойство дифференциальных операторов, также называется тождеством Лейбница.

Правила дифференцирования частного

/нету ответа/

Правила дифференцирования сложной функции

Пусть

функция x = f(t) дифференцируема в точке t, а функция y = f(x) дифференцируема в соответствующей точке x = f(t). Тогда сложная функция y = f(f(t)) дифференцируема в точке t, причем справедлива формула (f(f(t)))’ = f'(x)f'(t).

Механический смысл производной

Коротко говорят: производная от координаты по времени есть скорость. В этом состоит механический смысл производной.

Производная второго порядка и её механический смысл.

/Нету ответа/

Геометрический смысл производной

Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Понятия наибольшего и наименьшего значения функции

Наибольшее и наименьшее значения функции, понятия математического анализа. Значение, принимаемое функцией в некоторой точке множества, на котором эта функция задана, называется наибольшим (наименьшим) на этом множестве, если ни в какой другой точке множества функция не имеет большего (меньшего) значения.

Исследование функции

Слово «экстремум» значит крайний. Точкой экстремума называется такая точка, в которой функция принимает крайние значения: наибольшее или наименьшее.

Построение графиков функции

1.Найти область определения и область значений функции.

Выяснить, является ли функция четной (нечетной).

Выяснить, является ли функция периодической.

Найти точку пересечения графика функции с осью ординат.

Найти нули функции и промежутки знакопостоянства.

Вычислить производную функции и определить точки, в которых могут существовать экстремумы.

Найти промежутки монотонности функции.

Определить экстремумы функции.

Вычислить вторую производную

Определить точки перегиба.

Найти асимптоты графика.

Откуда

f(x) ≈ f(x0) + f'(x0)·Δx

Первообразная

Первообра́зной[1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Способ подстановки.

/практика/

Векторные величины.

24.1В линейной алгебре вектор — это элемент векторного пространства (или иначе: линейного пространства). Векторы можно складывать и умножать на число. Вектор также можно представить в виде линейной комбинации других векторов

Векторная величина — физическая величина, которая по форме представляет собой (одномерный) вектор. Противопоставляется с одной стороны скалярной (0-мерная), с другой — тензорными величинами (2- и более мерные матрицы). Примеры векторных физических величин: скорость, сила, поток тепла.

Действия над векторами.

Вектором наз. упорядоченная совокупность чисел Х={X1,X2,…Xn} вектор дан в n-мерном пространстве. Т(X1,X2,X3). n=1,2,3. Геометрический вектор – направленный отрезок. |AB|=|a| – длинна. 2 вектора наз. коллинеарными, если они лежат на 1 прямой или ||-ных прямых. Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях. 2 вектора равны, когда они коллинеарны, сонаправленны, и имеют одинак-уюдлинну.

1.умножение на число: произведение вектора А на число l наз. такой вектор В, который обладает след.св-ми: а) А||В. б) l>0, то АВ, l<0, то А¯В. в)l>1, то А<<spanstyle=”TEXT-DECORATION: underline”>В, )l<1, то АВ. 2. Разделить вектор на число n значит умножить его на число, обратное n: а/n=a*(1/n).

Предел переменной величины

Основные свойства пределов

Предел постоянной величины – Предел постоянной величины равен самой постоянной величине

cyberpedia.su

Арифметические свойства конечных пределов последовательностей

Пусть существуют конечные пределы и числовых последовательностей {x_n} и {y_n}. Тогда существуют пределы суммы, разности и произведения последовательностей, которые равны, соответственно, сумме, разности и произведению их пределов. Если b ≠ 0 и y_n ≠ 0 для всех n, то существует предел частного последовательностей, равный частному пределов:
(1) ;
(2) ;
(3) , если и ;
(4) .
Здесь C – постоянная, то есть заданное число.

Если , то .

Формулировки всех определений, теорем и свойств сходящихся последовательностей собраны на странице
Предел последовательности – основные теоремы и свойства.

Доказательство арифметических свойств

При доказательстве свойств, мы будем использовать определение предела последовательности:
.

Поскольку существует предел , то имеется функция такая, что для любого положительного числа ε₁ выполняется неравенство:
(5) при .

Поскольку существует предел , то имеется функция такая, что для любого положительного числа ε₂ выполняется неравенство:
(6) при .

Предел суммы и разности числовых последовательностей

Пусть существуют конечные пределы и последовательностей и . Тогда существуют пределы суммы и разности последовательностей {x_n &pm; y_n}, и они равны сумме и разности их пределов:
(1) .

Доказательство

Чтобы доказать свойство суммы и разности (1), нам нужно найти такую функцию , при которой, для любого положительного числа , выполняется неравенство:
(1.1) при .
При этом мы имеем функции и , при которых выполняются неравенства (5) и (6), для любых положительных и .

Воспользуемся известным неравенством
.
Преобразуем модуль разности в (1.1) и применим (5) и (6):
.
Последнее неравенство справедливо при и . Положим . Тогда, при и ,
.
Пусть, при заданном ε, есть наибольшее из чисел и . Тогда
при .

То есть мы нашли такую функцию , при которой, для любого положительного числа , выполняется неравенство:
(1.1) при .
Это и означает, что число a &pm; b является пределом последовательности .
Свойство доказано.

Предел произведения числовых последовательностей

Пусть существуют конечные пределы и числовых последовательностей и . Тогда существует предел произведения последовательностей {x_n· y_n}, и он равен произведению их пределов:
(2) .

Доказательство

Для доказательства свойства произведения (2), нам нужно найти такую функцию , при которой, для любого положительного числа , выполняется неравенство
(2.1) при .
При этом мы имеем функции и , при которых, для любых положительных и , выполняются неравенства (5) и (6):
(5) при ;
(6) при .

Преобразуем модуль разности в (2.1), применяя свойства неравенств:

.
Поскольку последовательность имеет конечный предел, то она ограничена некоторым положительным числом M_y: (см. Основные свойства пределов последовательностей). Применим (5) и (6). Тогда
.
Положим . Тогда при и ,
.
Пусть, при заданном ε, есть наибольшее из чисел и . Тогда
при .

То есть мы нашли такую функцию , при которой, для любого положительного числа , выполняется неравенство:
(2.1) при .
Это и означает, что число является пределом последовательности .
Свойство доказано.

Вынесение постоянной за знак предела

Пусть существует конечный предел числовой последовательности . И пусть последовательность образована из , умножением ее на постоянное число C. Тогда постоянную C можно выносить за знак предела:
(4) .

Доказательство

Это свойство является следствием свойства произведения последовательностей. Для доказательства рассмотрим последовательность, все элементы которой равны числу C: . Предел этой последовательности равен этому числу:

(см. Основные свойства пределов последовательностей).

Применим свойство произведения последовательностей:
.
Свойство доказано.

Предел частного числовых последовательностей

Пусть существуют конечные пределы и числовых последовательностей и . Причем и для всех n. Тогда существует предел частного последовательностей {x_n / y_{}, и он равен частному их пределов:
(3) .}

Доказательство

Для доказательства свойства частного (3), нам нужно найти такую функцию , при которой, для любого положительного , выполняется неравенство:
(3.1) при .
При этом мы имеем функции и , при которых, для любых положительных и , выполняются неравенства (5) и (6):
(5) при ;
(6) при .

Преобразуем модуль разности в (3.1), применяя свойства неравенств:

.
Тем самым мы получили следующую оценку:
(3.2) .

Сделаем оценку для . Подставим в (6) :
при .
Заметим, что есть расстояние между точками и на числовой прямой. Поскольку расстояние между точками и равно а расстояние между точками и меньше : , то расстояние между точками и больше :
, или
.
Это неравенство можно получить и другим способом. Применяя свойства неравенств и соотношение имеем:
;
;
.
Итак, мы нашли, что
при ,
где . Тогда
(3.3) при .

Подставим (5), (6) и (3.3) в (3.2):
.
Это неравенство выполняется при одновременном выполнении трех неравенств:
.
Подставим , . И пусть обозначает максимальное из чисел . Тогда
.

То есть мы нашли такую функцию
,
при которой, для любого положительного , выполняется неравенство
(3.1) при .
Это и означает, что число a/b является пределом последовательности .
Свойство доказано.

Предел последовательности из элементов, взятых по модулю

Пусть существует конечный предел числовой последовательности . И пусть последовательность составлена из элементов , взятых по абсолютной величине. Тогда
.

Доказательство

Для доказательства этого свойства, нам нужно найти такую функцию , при которой, для любого положительного , выполняется неравенство:
при .
При этом у нас есть функция , при которой выполняется неравенство (5):
(5) при .

Воспользуемся известным неравенством:

и применим (5):
.
Последнее выполняется при .
То есть мы можем взять .

Итак, для любого ,
при .
Свойство доказано.

Автор: Олег Одинцов. Опубликовано: 03-08-2017

1cov-edu.ru

Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.е.

, .

5) Если , , то предел сложной функции

6)Если в некоторой окрестности точки (или при достаточно больших ) , то

Вопрос

Основные приемы вычисления пределов

Вопрос

Первый замечательный предел

Функция не определена при x=0, так как числитель и знаменатель дроби обращаются в нуль. График функции изображен на рисунке.

Однако, можно найти предел этой функции при х→0.

Из первого замечательного предела следует эквивалентность при х →0 следующих бесконечно малых величин: ах, sinax; tgax; arcsinax; arctgax. Это означает, что предел отношения двух любых из этих функций при х →0 равен 1.

Вопрос

Второй замечательный предел

Определение. Числом (вторым замечательным пределом) называется предел числовой последовательности :

, где

Прямым вычислением можно убедиться, что , (иррациональное число, число Эйлера).

Если рассмотреть функцию , то при функция имеет предел, равный числу :

Или если , то .

Непосредственное вычисление этого предела приводит к неопределенности . Однако доказано, что он равен числу . Второй замечательный предел необходимо всегда использовать при раскрытии неопределенности вида .

Число (число Эйлера, неперово число) играет важную роль в математическом анализе. График функции

Рассмотрим примеры вычисления пределов. Получил название экспоненты. Широко используются логарифмы по основанию , называемые натуральными. Натуральные логарифмы обозначаются символом .

Пример. .

Пример. = .

Пример. .

Пример.

Пример. .

Вопрос

Эквивалентные бесконечно малые

Вопрос

Непрерывность функции

Определение 1. Функция называется непрерывной в точке

, если она удовлетворяет следующим условиям:

1) определена в точке , т.е. существует ;

2) имеет конечные односторонние пределы функции при слева и справа;

3) эти пределы равны значению функции в точке , т.е.

Пример.Исследовать функции на непрерывность в точке :

а) , б) .

Решение. а) . При функция определена, , , , т.е. все три условия непрерывности функции в точке выполнены. Следовательно, функция в точке непрерывна.

б) . При функция не определена; ; .

Т.о. в точке функция не является непрерывной, т.к. не выполнены первое и третье условия непрерывности функции в точке.

Определение 2. Функция называется непрерывной в точке , если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: .

Определения 1 и 2 равносильны.

Точка называется точкой разрыва функции , если эта функция в данной точке не является непрерывной. Различают точки разрыва:

Первого рода – когда существуют конечные односторонние пределы функции слева и справа при , не равные друг другу. К точкам разрыва первого рода относятся также точки устранимого разрыва, когда предел функции при существует, но не равен значению функции в этой точке.

Второго рода – когда хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует.

cyberpedia.su

3. Основные свойства пределов | Решение задач по математике и другим п

1. Последовательность называется постоянной, если все её члены равны постоянному числу , т. е. , при всех . Предел постоянной последовательности равен постоянному числу , т. е. если , то .

2. Если , то , где – бесконечно малая последовательность.

3. Если последовательность имеет предел, то она ограничена, т. е. если , то , где – некоторое положительное число.

4. Если последовательность имеет предел, то он один.

5. Предел суммы двух последовательностей равен сумму их пределов, если предел каждого слагаемого существует, т. е.

Если пределы справа существуют.

Следствие. Предел суммы конечного числа последовательностей, имеющих предел, равен сумме их пределов.

6. Предел произведения двух сходящихся последовательностей равен произведению их пределов, т. е.

Если пределы справа существуют.

Следствие 1. Постоянный множитель можно выносить за знак предела, т. е.

Следствие 2. Предел произведения конечного числа сходящихся последовательностей равен произведению пределов сомножителей.

Следствие 3. Предел степени последовательности, имеющей предел, равен степени предела последовательности, т. е.

Если существует и – конечное число.

Следствие 4. Предел корня из сходящейся последовательности равен корню той же степени из предела последовательности, т. е.

Если предел справа существует (предполагается также, что корни слева и справа существуют, т. е. если корни являются корнями четной степени, то подкоренные выражения неотрицательны).

7. Предел частного двух сходящихся последовательностей равен частному их пределов, если предел делителя не равен нулю, т. е.

Если пределы справа существуют и .

В тех случаях, когда пределы отдельных последовательностей, над которыми производятся действия, не существуют, то это еще не означает, что не существует общий предел (предел результата действий). Последний может существовать, только он не может быть найден с помощью указанных свойств пределов; его следует находить в каждом отдельном случае особыми приемами.

То же самое можно сказать и о пределе частного, когда пределы делимого и делителя равны нулю.

Рассмотрим примеры на нахождение пределов последовательностей.

Пример 7. Дана последовательность . Доказать, что .

Доказательство. Пусть задано . Найдём разность

По определению предела должно выполняться неравенство

Откуда

Следовательно, , если . Поэтому .

Находить пределы последовательностей, пользуясь непосредственно определением предела, нецелесообразно. Рассмотренный предел можно найти, применяя свойства пределов:

Обычно все промежуточные выкладки опускают, и решение выглядит так:

Пример 8. Найти предел .

Решение. Рассмотрим отдельно три случая:

а) Пусть ; тогда

б) Пусть ; тогда

в) Пусть ; тогда

Ответ:

Пример 9. Найти предел .

Решение. Вынося старшие степени числителя и знаменателя за скобки, имеем:

Пример 10. Найти предел .

Решение. Применить непосредственно свойства пределов здесь нельзя. Чтобы найти данный предел, умножим и разделим выражение, стоящее под знаком предела, на сопряженное ему, тогда

(второй предел равен нулю).

Следовательно, числитель есть общий член бесконечно малой последовательности. Так как знаменатель – общий член бесконечно большой последовательности, то последовательность бесконечно мала, а ее предел равен нулю.

Ответ: .

Пример 11. Найти предел .

Решение. Частное от деления ограниченной последовательности на бесконечно большую есть бесконечно малая последовательность (свойство 6 бесконечно малых последовательностей). Поэтому предел равен нулю.

Ответ: .

Иногда при нахождении пределов формальные преобразования не достигают цели и нужно рассмотрение по существу. Например, при изучении выражений, содержащих , при , надо иметь в виду, что при значение при , а при значение неограниченно растет.

Пример 12. Найти .

Решение. Рассмотрим отдельно три случая:

а) Пусть ; тогда

б) Пусть ; тогда

в) Пусть ; тогда

Ответ:

< Предыдущая		Следующая >

matica.org.ua

Как считать пределы

Содержание

Инструкция

В учебниках по математическому анализу значительное внимание уделяется приемам вычисления пределов функций и последовательностей. Существуют готовые правила и методы, применяя которые, можно с легкостью решать даже относительно сложные задачи на пределы.

Инструкция

В математическом анализе существуют понятия пределов последовательностей и функций. Когда требуется найти предел последовательности, это записывают следующим образом: lim xn=a. В такой последовательности последовательности xn стремится к a, а n к бесконечности. Последовательность обычно представляют в виде ряда, например:
x1, x2, x3…,xm,…,xn… .
Последовательности подразделяются на возрастающие и убывающие. Например:
xn=n^2 – возрастающая последовательность
yn=1/n – убывающая последовательность
Так, например, предел последовательности xn=1/n^2 равен:
lim 1/n^2=0x→∞
Данный предел равен нулю, поскольку n→∞, а последовательность 1/n^2 стремится к нулю.
Обычно переменная величина x стремится к конечному пределу a, причем, x постоянно приближается к a, а величина a постоянна. Это записывают следующим образом: limx =a, при этом, n также может стремиться как к нулю, так и к бесконечности. Существуют бесконечные функции, для них предел стремится к бесконечности. В других случаях, когда, например, функцией описывается замедление хода поезда, можно говорить о пределе, стремящемся к нулю.
У пределов имеется ряд свойств. Как правило, любая функция имеет только один предел. Это главное свойство предела. Другие их свойства перечислены ниже:
* Предел суммы равен сумме пределов:
lim(x+y)=lim x+lim y
* Предел произведения равен произведению пределов:
lim(xy)=lim x*lim y
* Предел частного равен частному от пределов:
lim(x/y)=lim x/lim y
* Постоянный множитель выносят за знак предела:
lim(Cx)=C lim x
Если дана функция 1 /x, в которой x →∞, ее предел равен нулю. Если же x→0, предел такой функции равен ∞.
Для тригонометрических функций имеются исключения из этих правил. Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество:
lim sin x/x=1x→0
В ряде задач встречаются функции, при вычислении пределов которых возникает неопределенность – ситуация, при которой предел невозможно вычислить. Единственным выходом из такой ситуации становится применение правила Лопиталя. Существует два вида неопределенностей:
* неопределенность вида 0/0
* неопределенность вида ∞/∞
К примеру, дан предел следующего вида: lim f(x)/l(x), причем, f(x0)=l(x0)=0. В таком случае, возникает неопределенность вида 0/0. Для решения такой задачи обе функции подвергают дифференцированию, после чего находят предел результата. Для неопределенностей вида 0/0 предел равен:
lim f(x)/l(x)=lim f'(x)/l'(x) (при x→0)
Это же правило справедливо и для неопределенностей типа ∞/∞. Но в этом случае справедливо следующее равенство: f(x)=l(x)=∞
С помощью правила Лопиталя можно находить значения любых пределов, в которых фигурируют неопределенности. Обязательное условие притом – отсутствие ошибок при нахождении производных. Так, например, производная функции (x^2)’ равна 2x. Отсюда можно сделать вывод, что:
f'(x)=nx^(n-1)

completerepair.ru

Предел равен – Калькулятор онлайн – Решение пределов

Предел постоянной величины – Предел постоянной величины равен самой постоянной величине — КиберПедия