Пределы с синусами как решать – .
Тригонометрические пределы. Первый замечательный предел
ПР13. Найдите тригонометрические пределы простой подстановкой:
1) а) 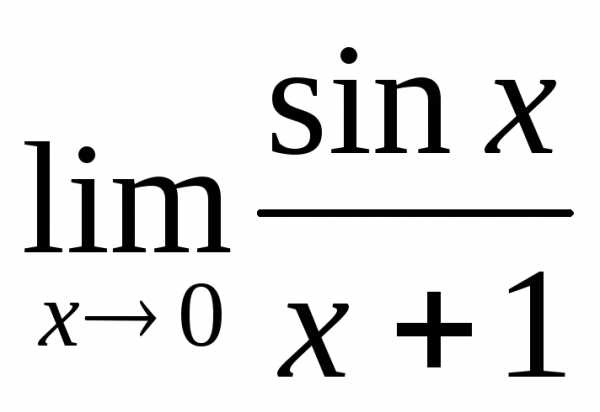 ; б)
; б)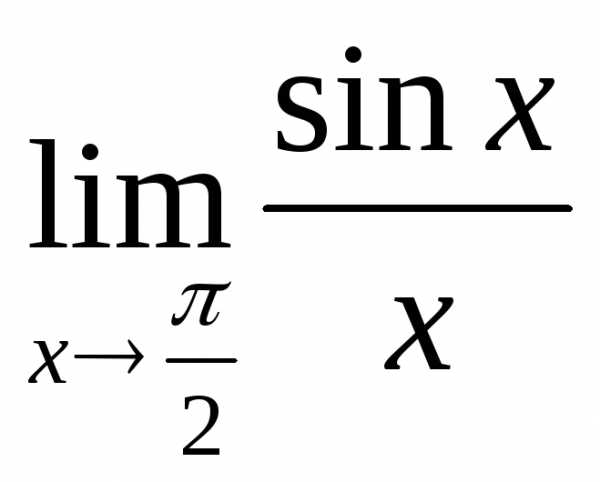 ; в)
; в)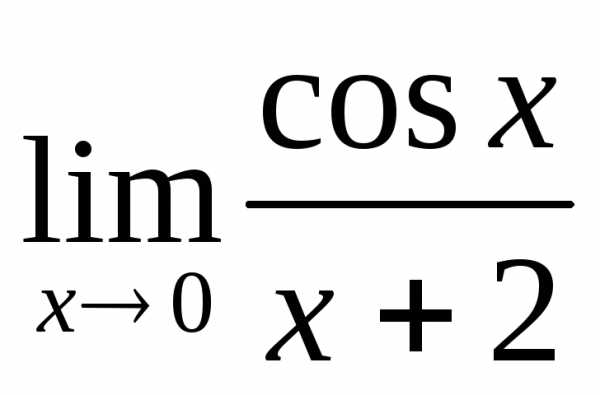 ; г)
; г)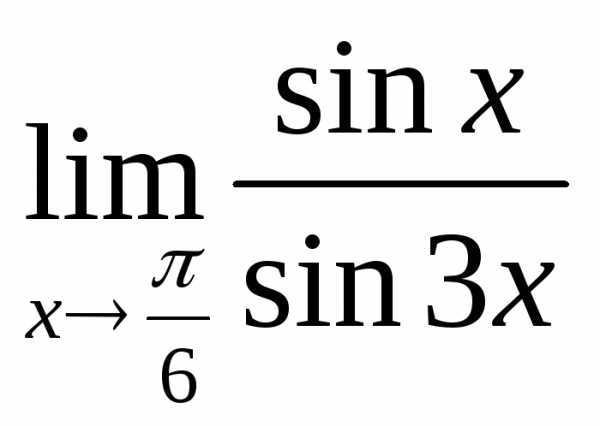 ;
д)
;
д)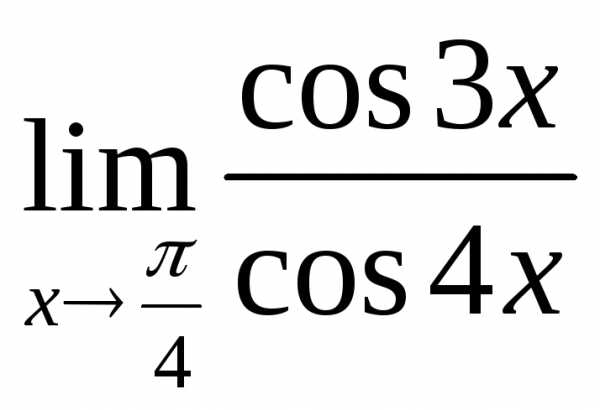 ;
;
2) а) 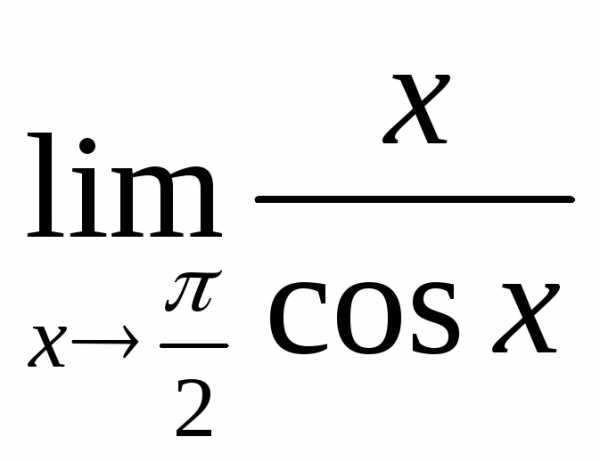 ; б)
; б)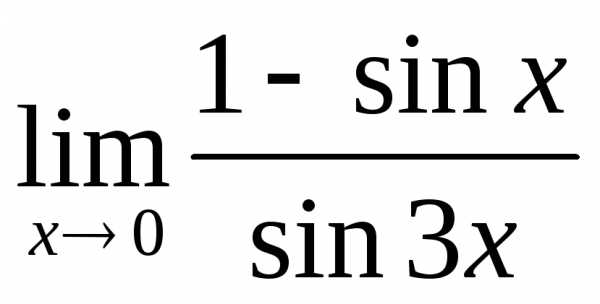 ; в)
; в)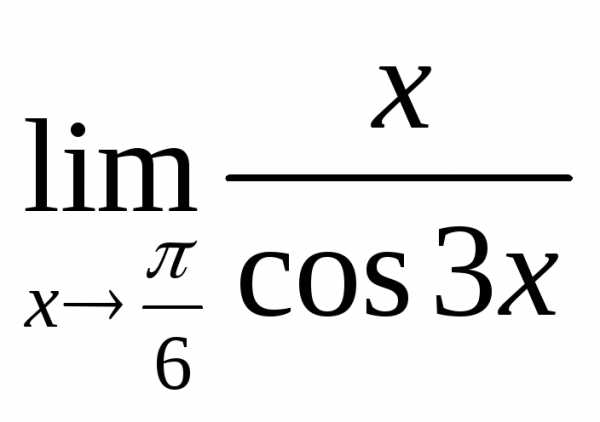 ; г)
; г)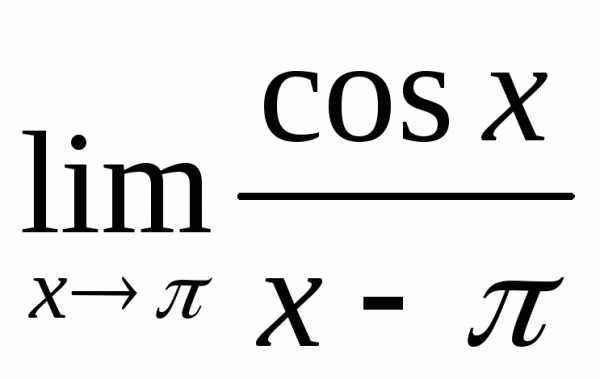 ;
д)
;
д)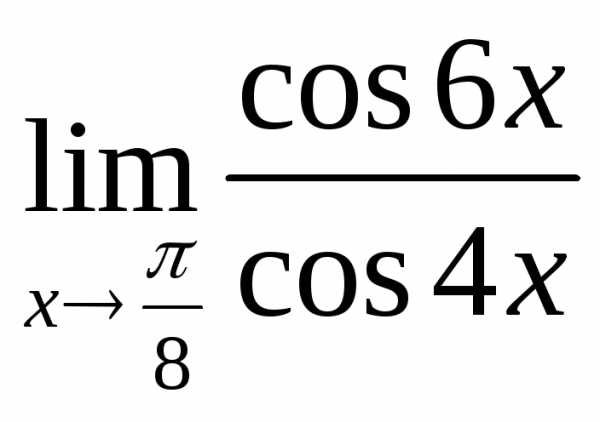
Пример 19. Легко видеть, что
а) ;
б) .
Предел 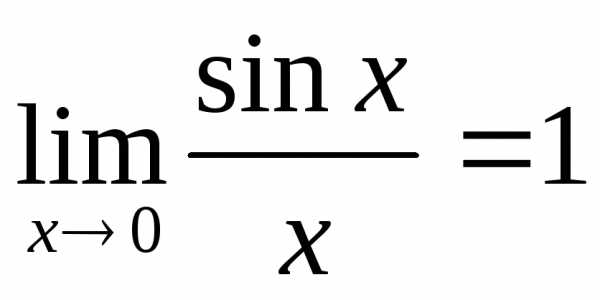 помогает, если при вычислении
тригонометрических функций получается
неопределённость
помогает, если при вычислении
тригонометрических функций получается
неопределённость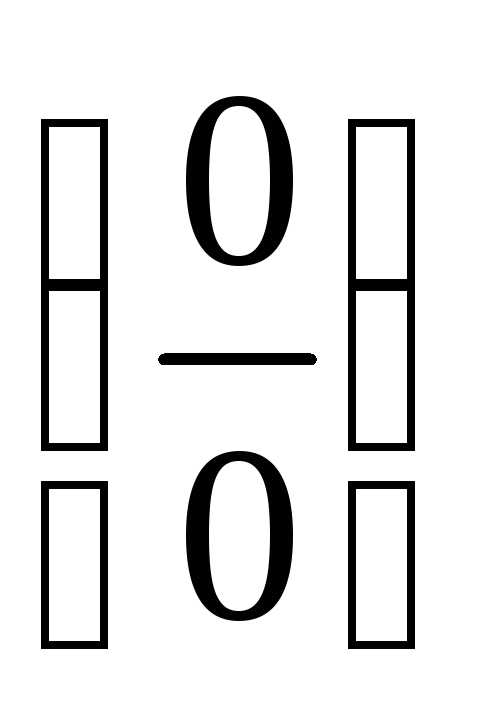 .
Оказывается, если прифункция
.
Оказывается, если прифункция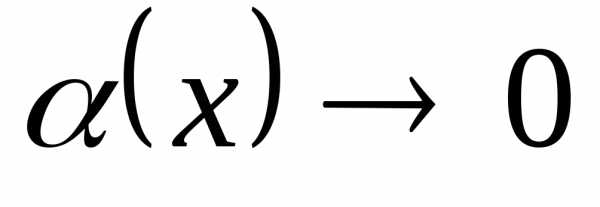 ,
то выполнено приближённое равенство
,
то выполнено приближённое равенство
,
и все 4 функции
примерно равны собственному аргументу.
Тем самым, если аргумент 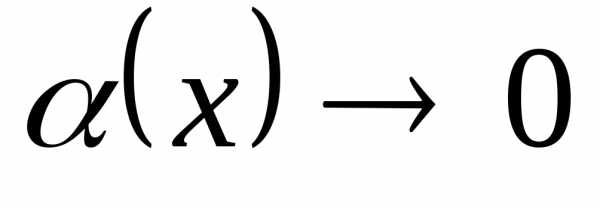 ,
указанные функции являютсяэквивалентными
бесконечно малыми (предел их соотношения равен 1).
,
указанные функции являютсяэквивалентными
бесконечно малыми (предел их соотношения равен 1).
Так, ,, поскольку. Как применить это при вычислении пределов, показано в примерах.
ПР14. Раскройте неопределённость 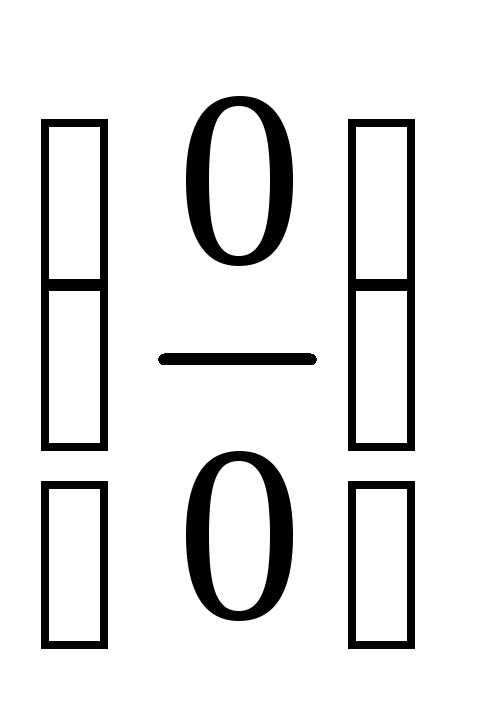
1) 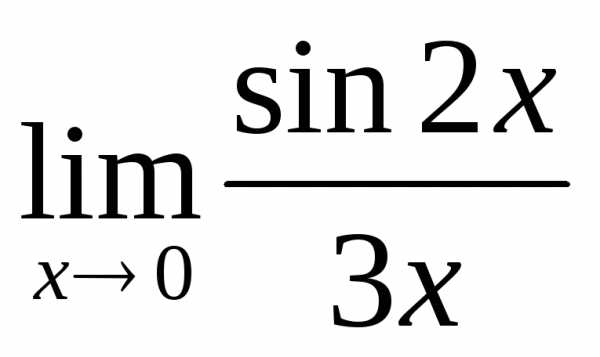 ; б)
; б)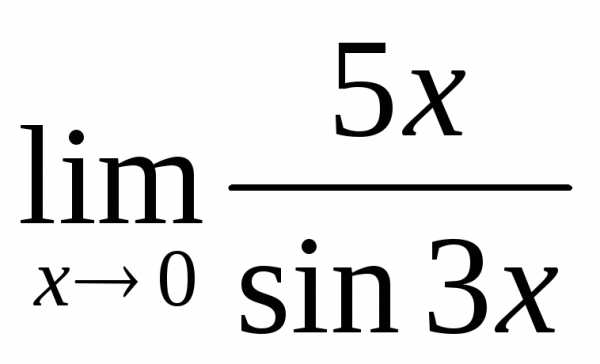 ; в)
; в)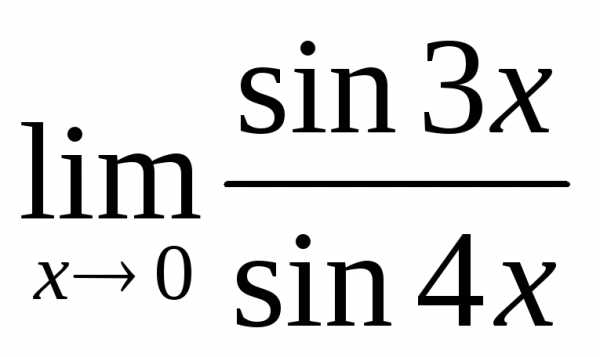 ; г)
; г)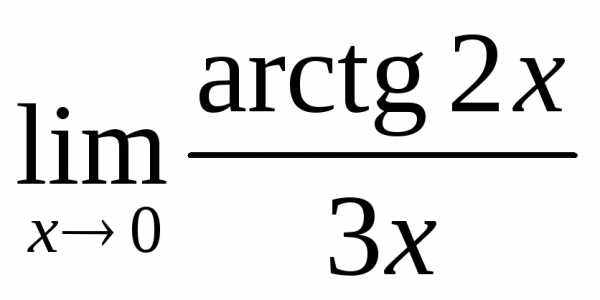 ; д)
; д)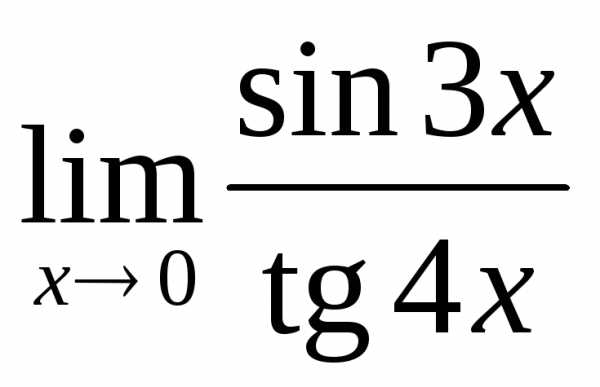 ;
;
2) 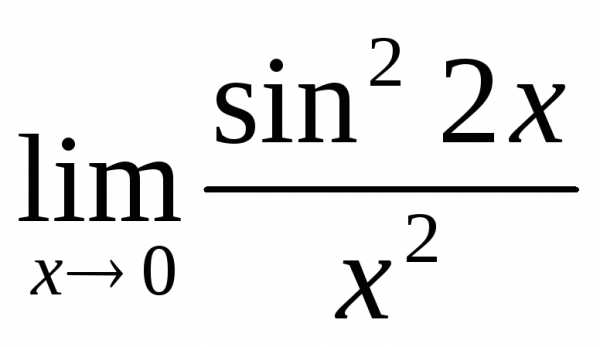 ; б)
; б)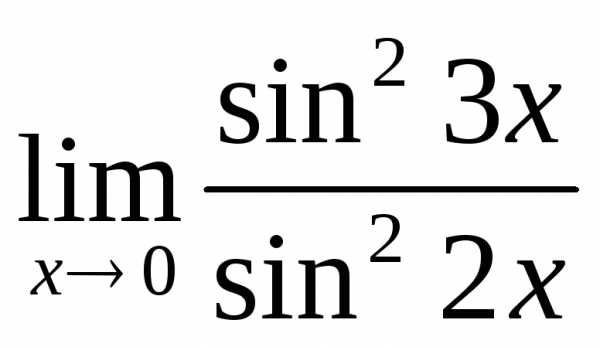 ; в)
; в)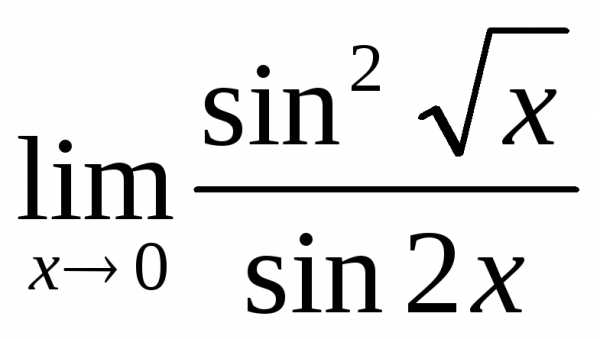 ; г)
; г)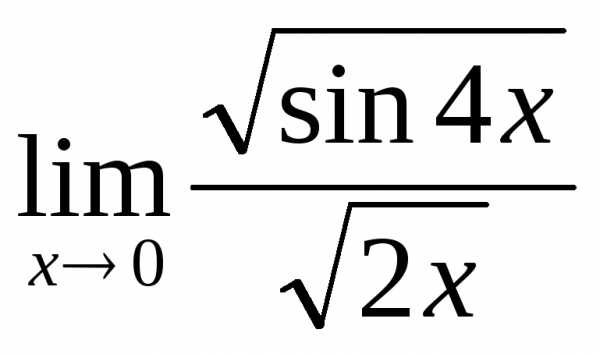 ; д)
; д)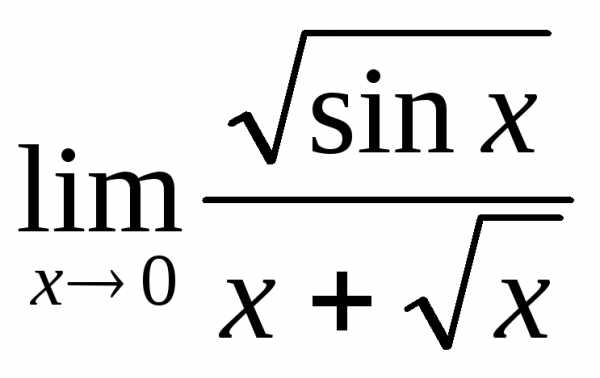 .
.
Пример 20. Если заменить функции собственным аргументом, то
а) ;
б) ;
в) .
ПР15. Раскройте неопределённость 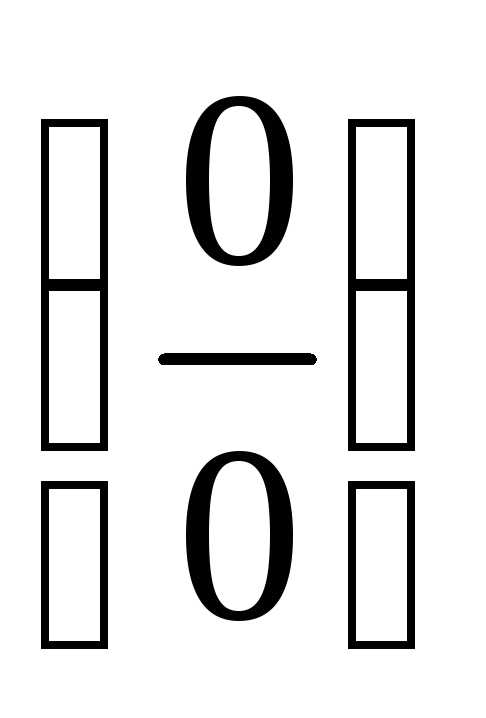 при помощи эквивалентных бесконечно
малых и тождества:
при помощи эквивалентных бесконечно
малых и тождества:
1) а) 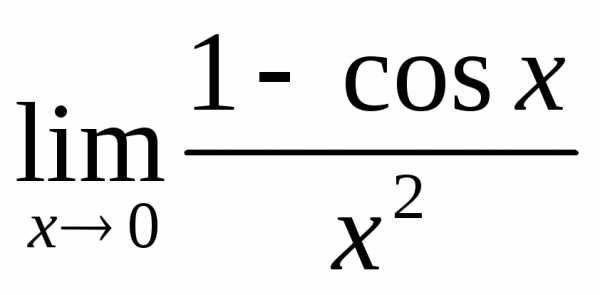 ; б)
; б)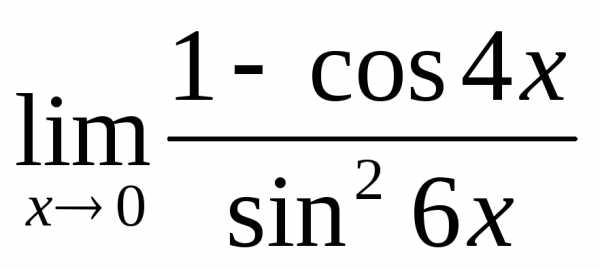 ; в); г)
; в); г)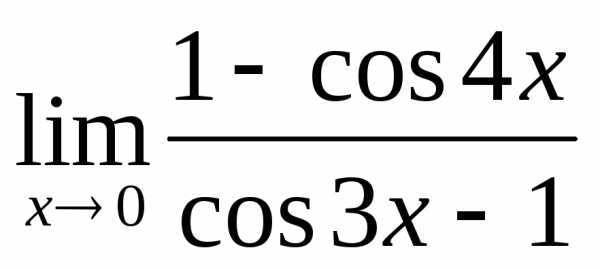 ;
;
2) а) 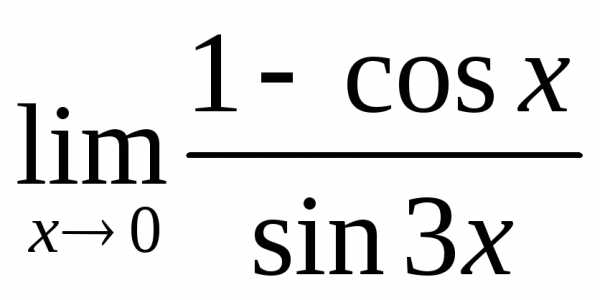 ; б)
; б)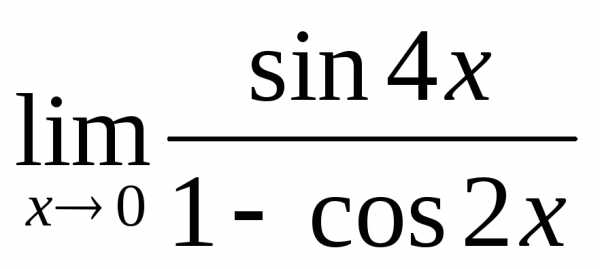 ; в)
; в)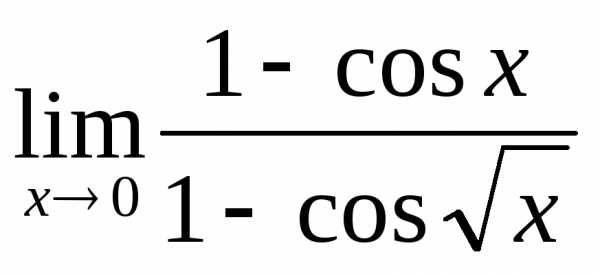 ; г)
; г)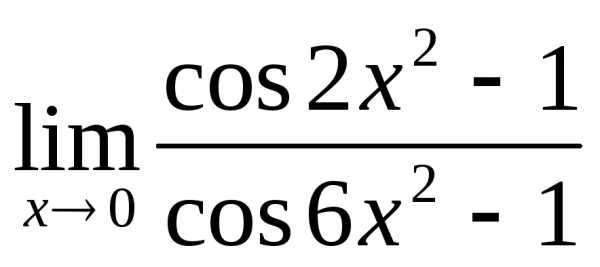 .
.
Пример 21.
.
Пример 22.
(учли, что по смыслу
задачи 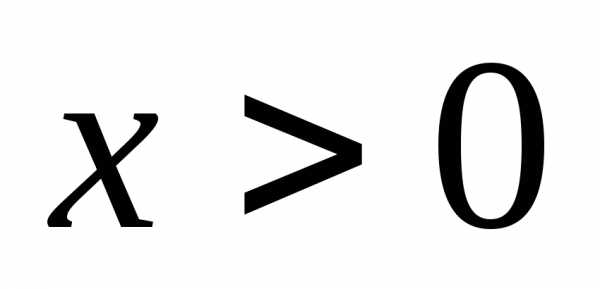
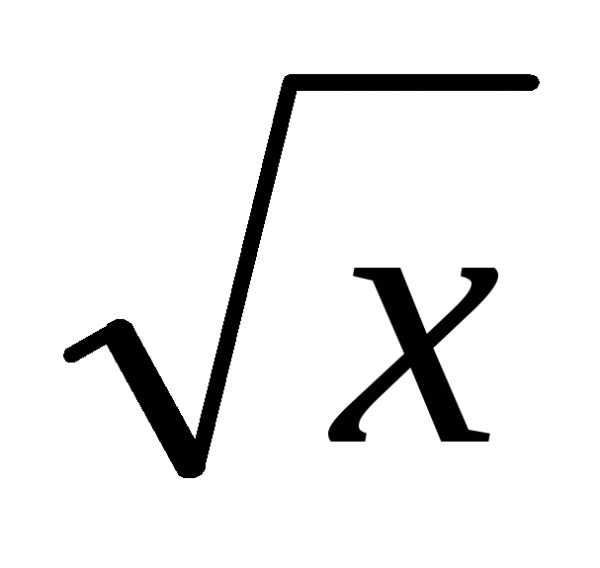 не существует).
не существует).При переходе к эквивалентным бесконечно малым следует проявлять осторожность, когда присутствует разность или сумма функций, тем более, если после упрощений получается 0 в числителе или знаменателе:
.
Попытка перейти
в числителе к разности  приведёт к ошибке: либо решим, что в
числителе «чистый» 0, и потому ответ
равен 0, либо вовсе зайдём в тупик.
приведёт к ошибке: либо решим, что в
числителе «чистый» 0, и потому ответ
равен 0, либо вовсе зайдём в тупик.
Второй замечательный предел
Предел
применяют для раскрытия неопределённостей
вида 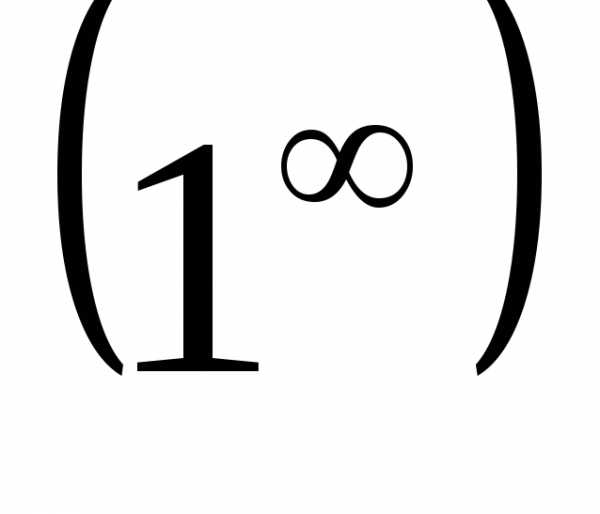 ,
связанных с показательными функциями
,
связанных с показательными функциями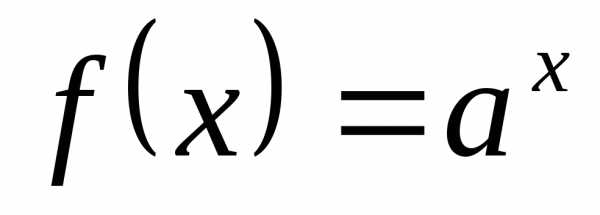 .
Равносильное
свойство:
.
Равносильное
свойство:
Однако, как при вычислении любого предела, начинать следует с подстановки предельной точки. Если вместо точки указана бесконечность, пытаются упростить пример, найдя предел основания, степени и т.п. И только при возникновении неопределённости применяют замечательный предел.
Схема применения 2-го замечательного предела
Пусть при 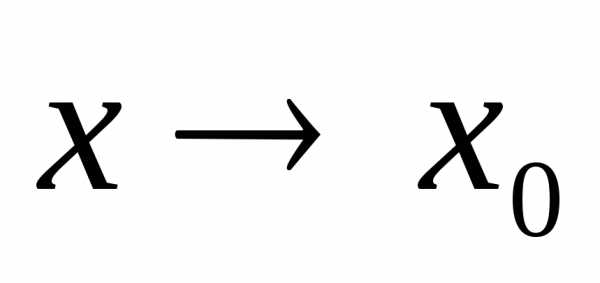 оказалось, что
оказалось, что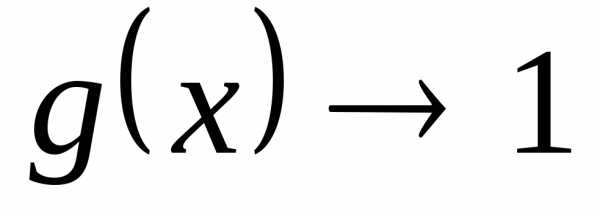 ,
а
,
а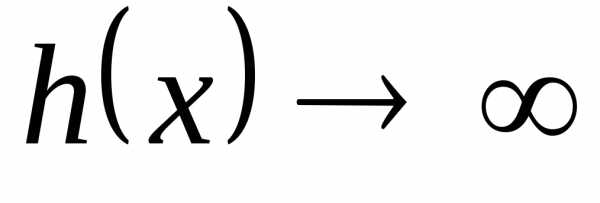 .
Тогда.
.
Тогда.
Считаем, что
,
где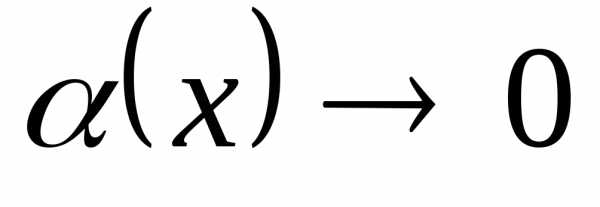 при
при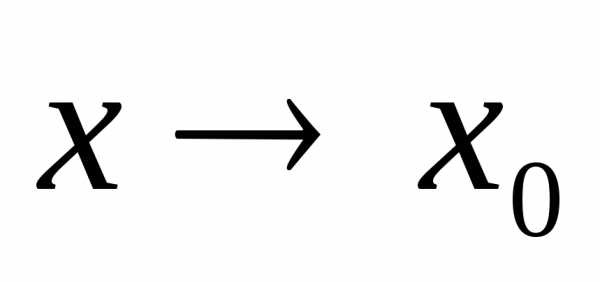 .
Тогда
.
Тогда
.
Поскольку , то.
Найдём предел 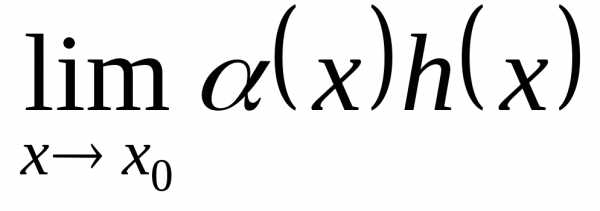 ,
и если он равен числу A,
то весь предел равен
,
и если он равен числу A,
то весь предел равен 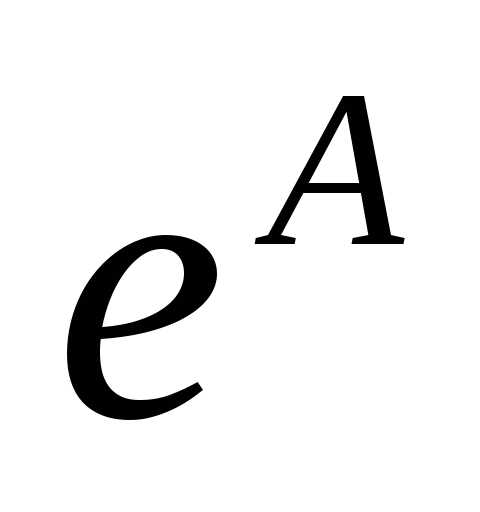 .
.
ПР16. Найдите пределы простой подстановкой:
1) а) 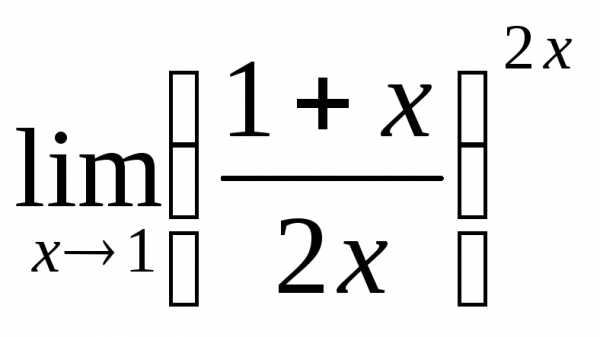 ; б)
; б)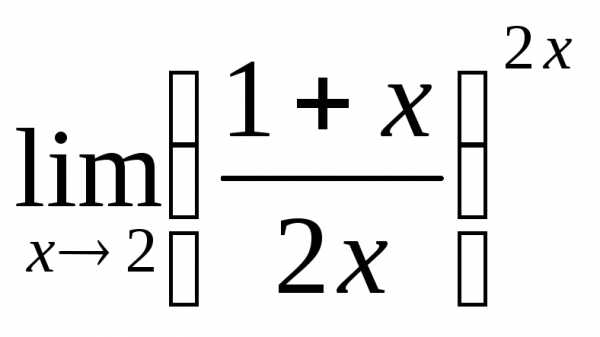 ; в)
; в)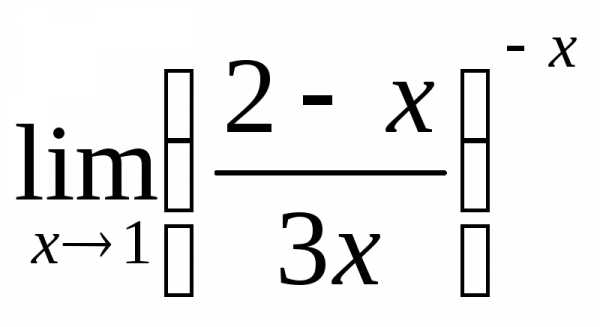 ; г)
; г)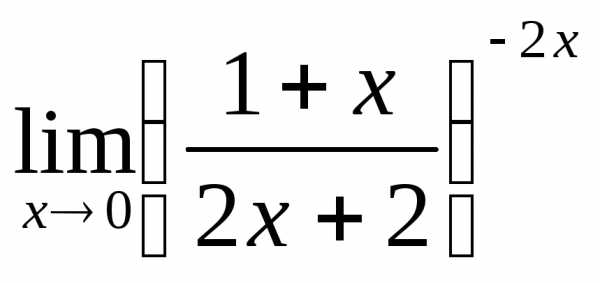 ;
;
2) а) 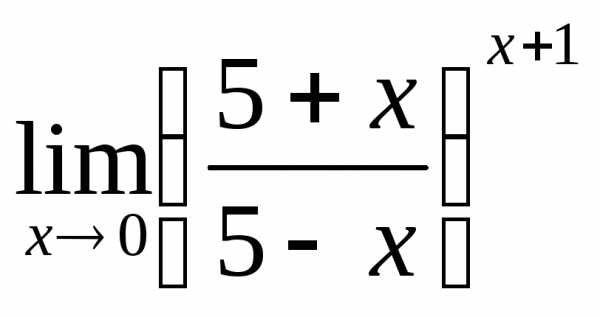 ; б)
; б)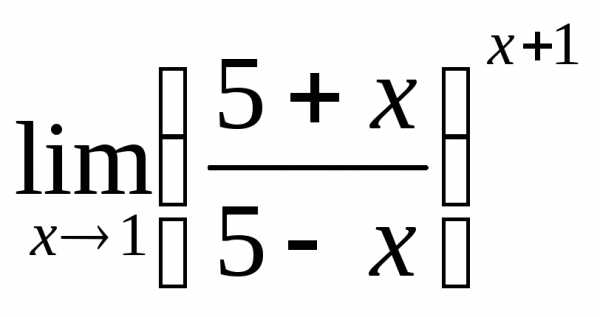 ; в)
; в)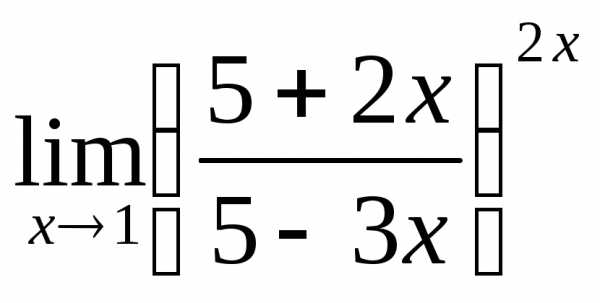 ; г)
; г)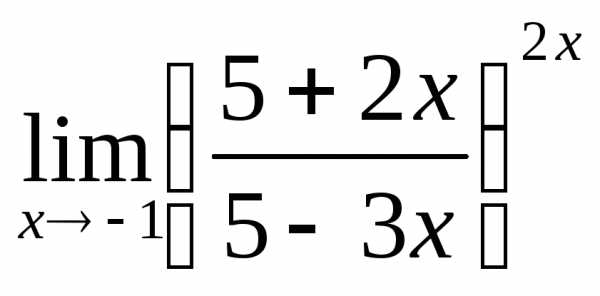 .
.
Пример 23. .
ПР17. Найдите пределы, воспользовавшись
свойствами показательной функции 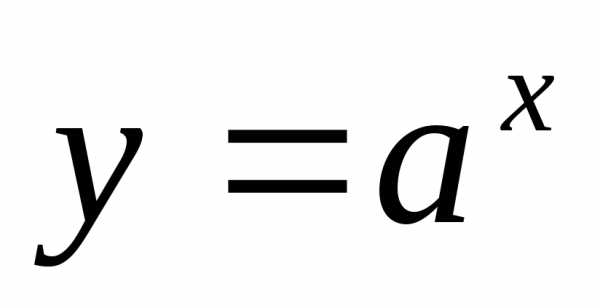
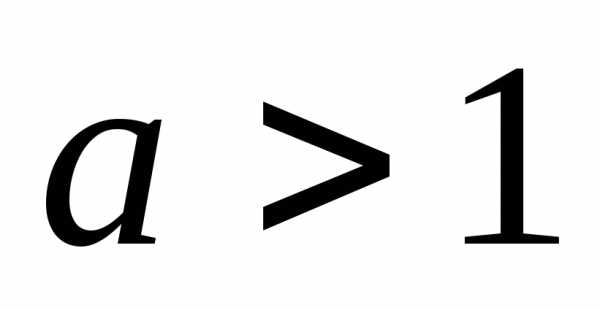 или:
или: 1) а) 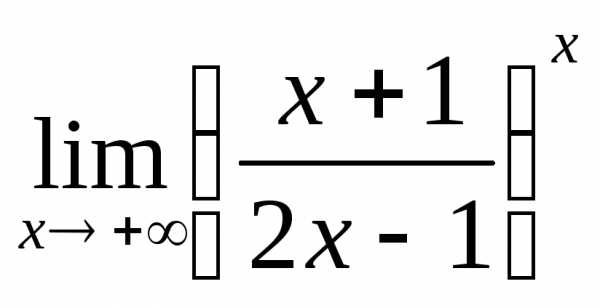 ; б)
; б)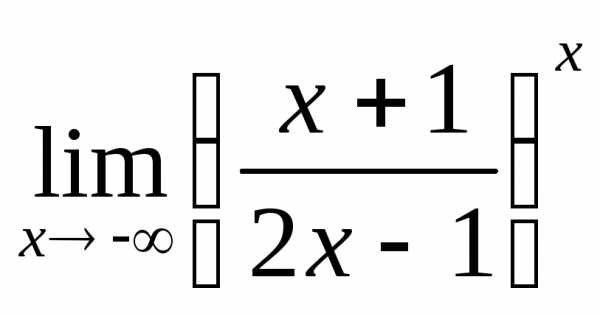 ; в)
; в)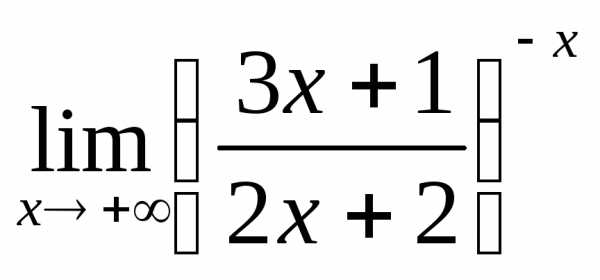 ; г)
; г)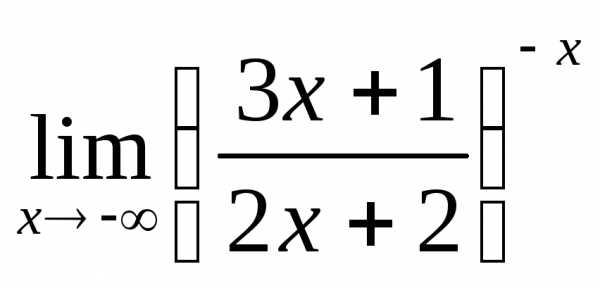 ;
;
2) а) 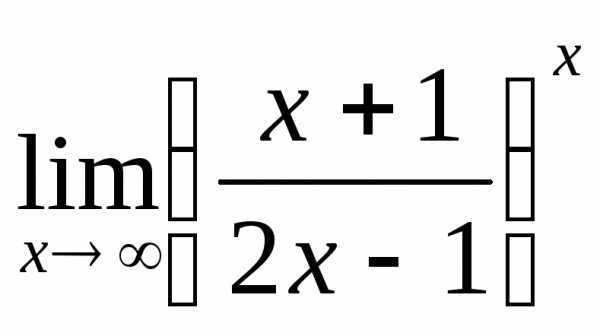 ; б)
; б)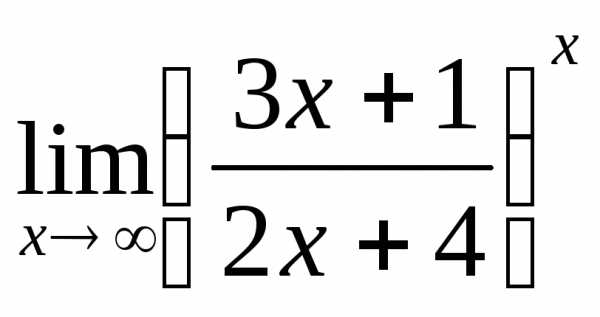 ; в)
; в)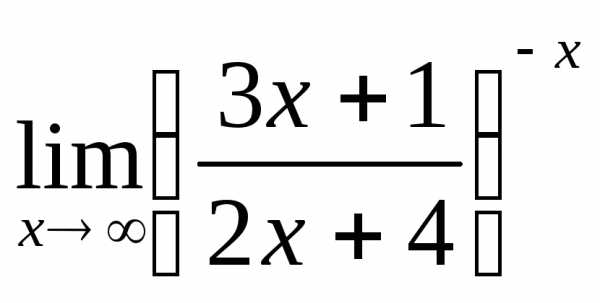 ; г)
; г)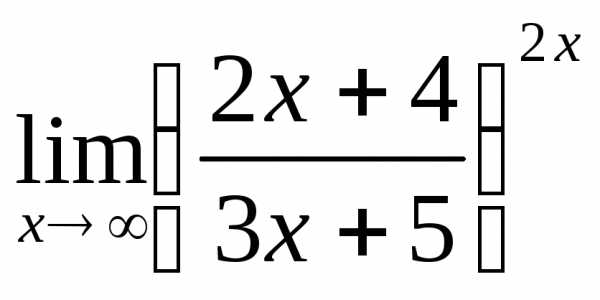 .
.
В задании 2 в каждом примере получаются 2 ответа – в зависимости от знака бесконечности.
Пояснение. Если 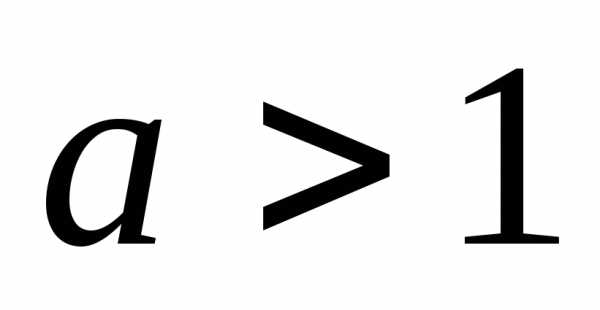
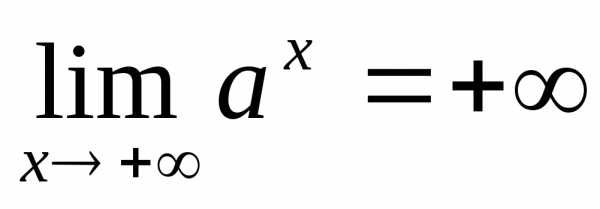 и
и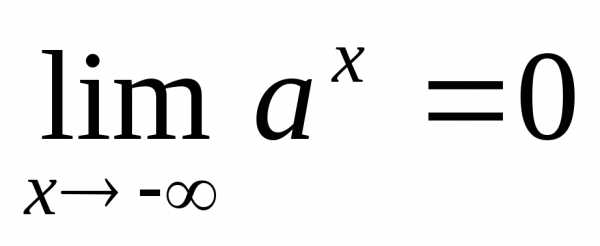 .
Если,
то
.
Если,
то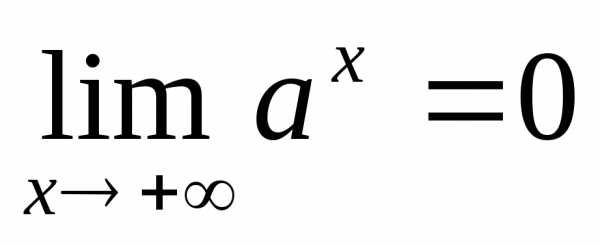 и
и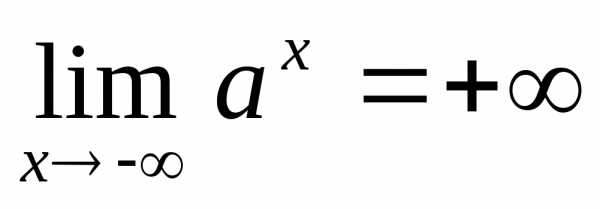 .
При
.
При зависимость
зависимость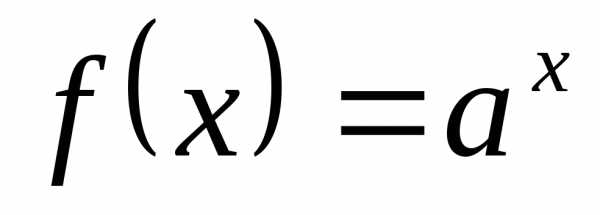 не является функцией (точнее, это функция,
разрывная в каждой действительной
точке).
не является функцией (точнее, это функция,
разрывная в каждой действительной
точке). Пример 24. 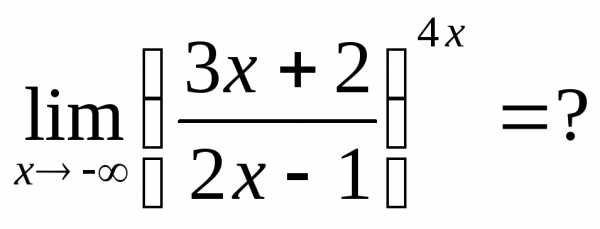 Видно, что
Видно, что
.
Тогда, поскольку
при
величина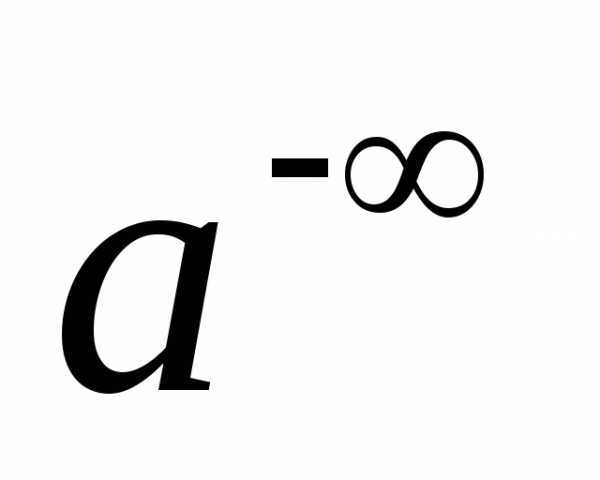 обращается в 0,
обращается в 0,
.
Пример 25. 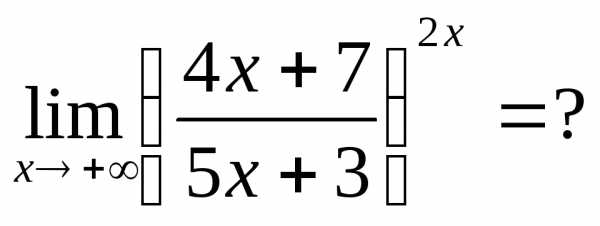
.
Основание
,
а в этом случае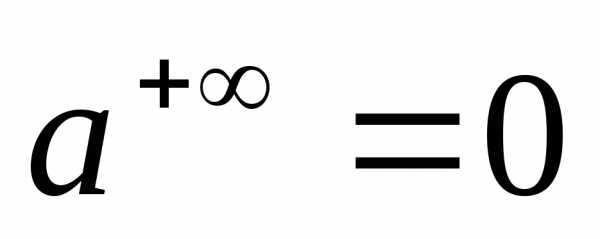 .
Поэтому
.
Поэтому
.
Пример 26. 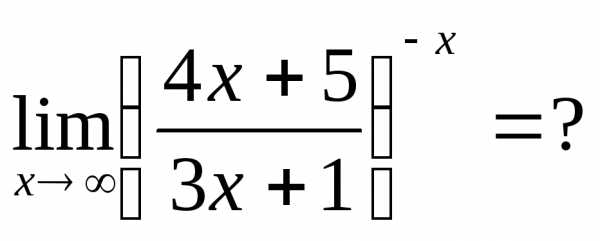 Здесь
Здесь
.
Но функция 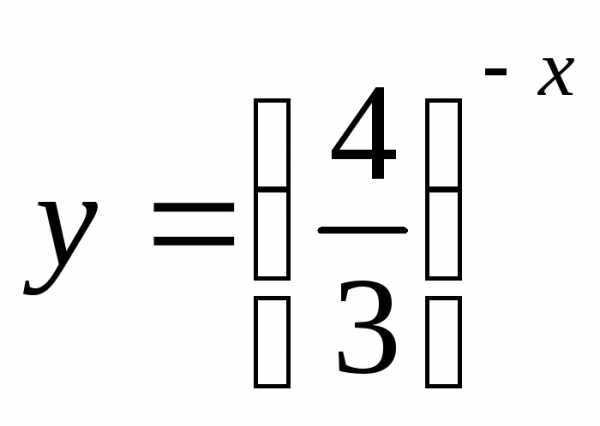 – это то же, что
– это то же, что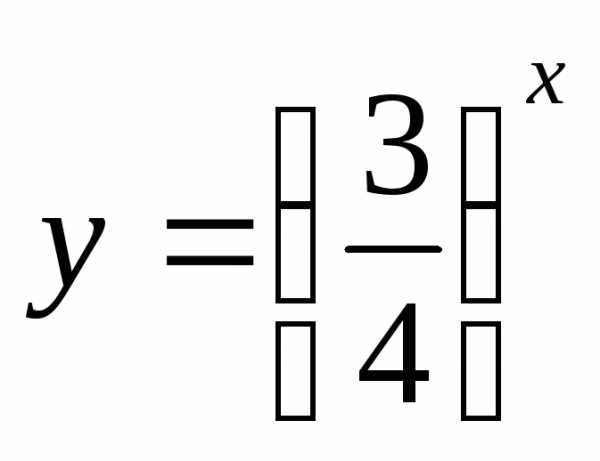 .
А эта функция стремится к 0 прии обращается в
.
А эта функция стремится к 0 прии обращается в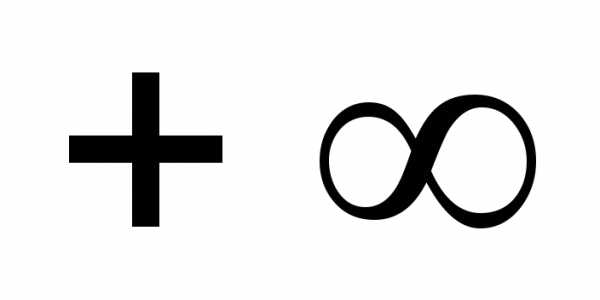 при.
Тогда.
при.
Тогда.
ПР18. При помощи 2-го замечательного предела раскройте неопределённость , когда аргумент стремится к бесконечности:
1) а) 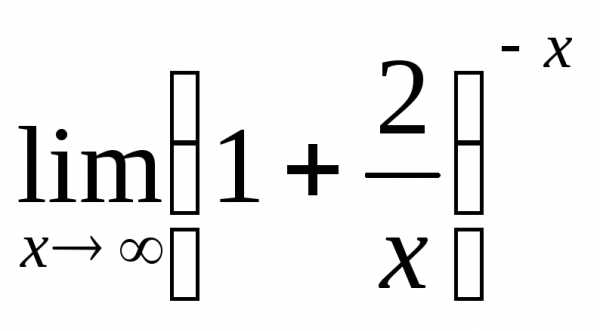 б)
б)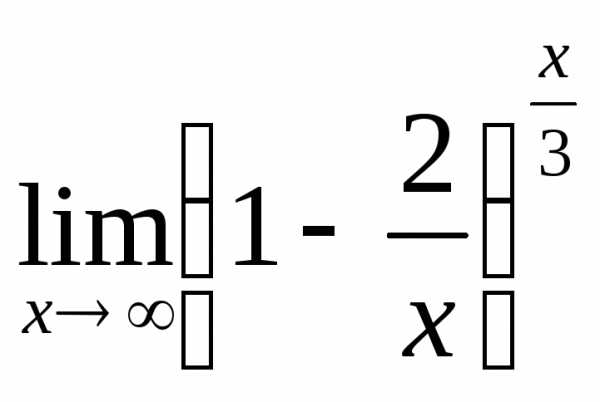 ; в)
; в)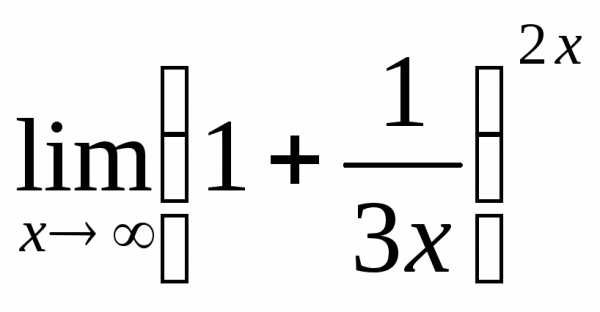
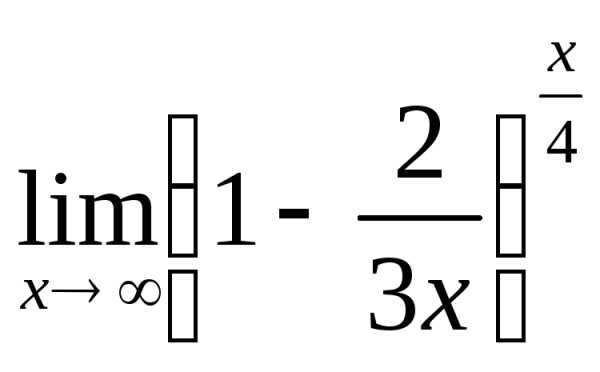 ;
; 2) а) 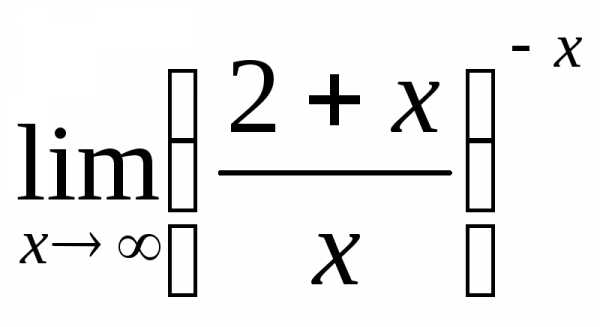 б)
б)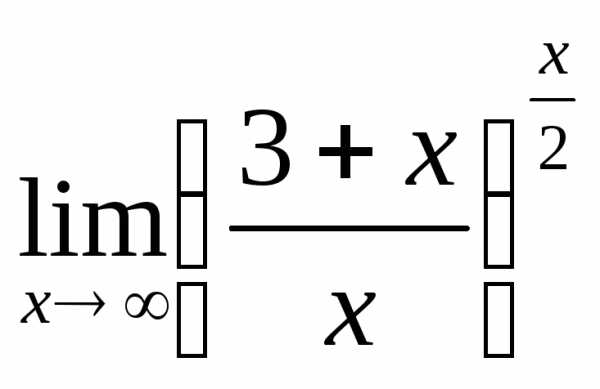 ; в)
; в)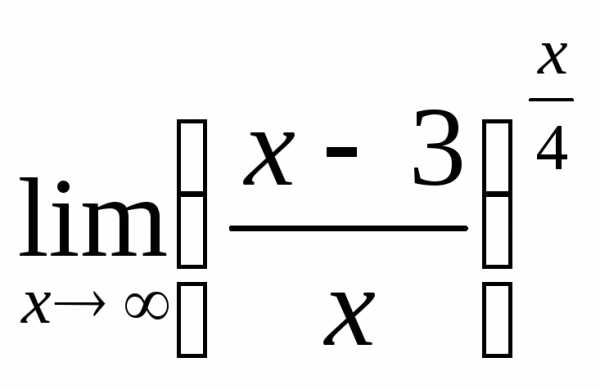 ; г)
; г)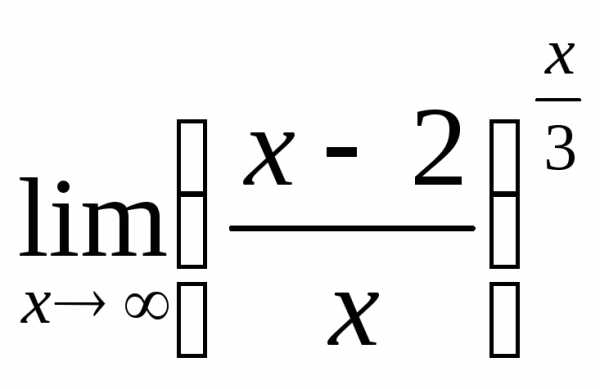 ;
;
3)а)  ; б)
; б)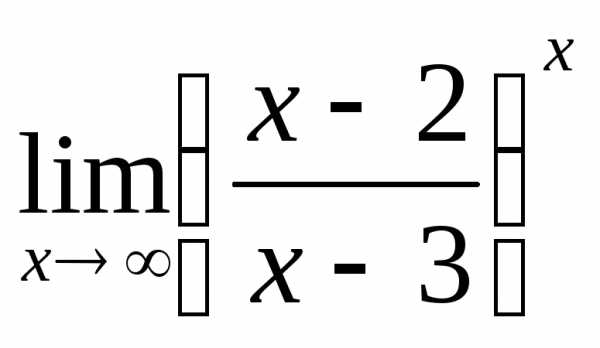 ; в)
; в)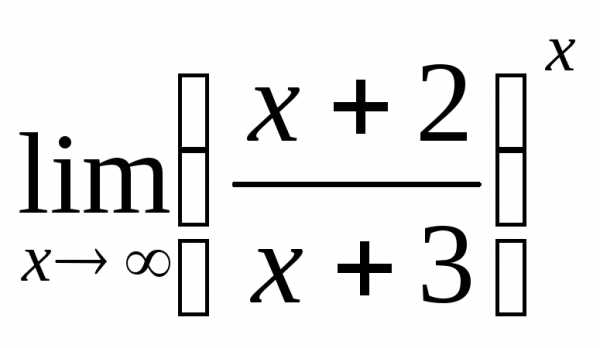 ; г)
; г)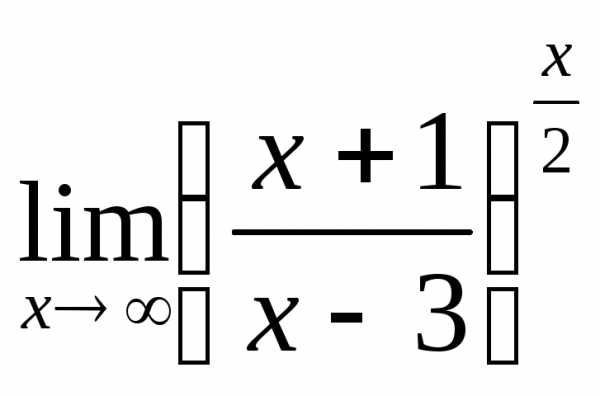 ;
;
4) а) 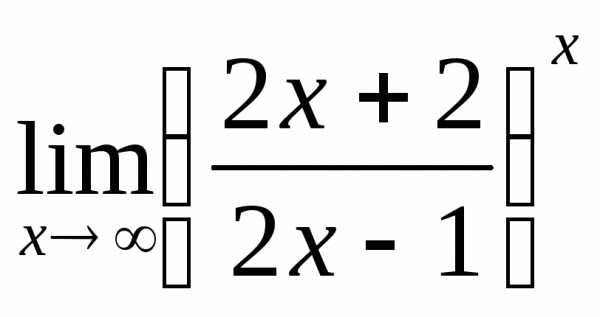 ; б)
; б)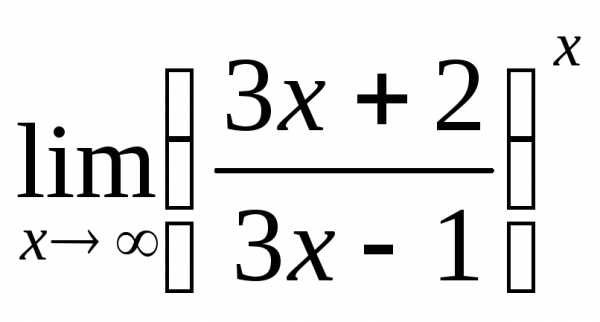 ; в)
; в)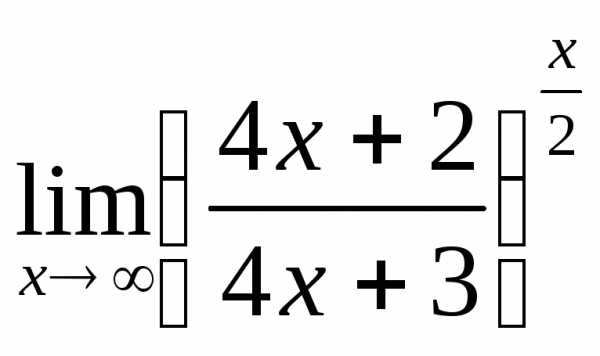
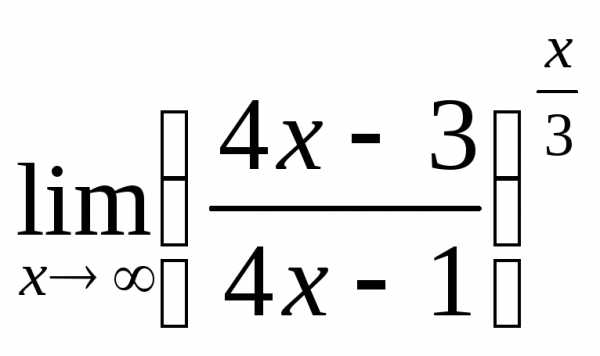 ;
; 5) а) 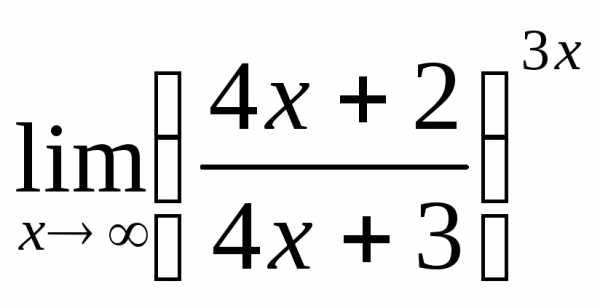 ; б)
; б)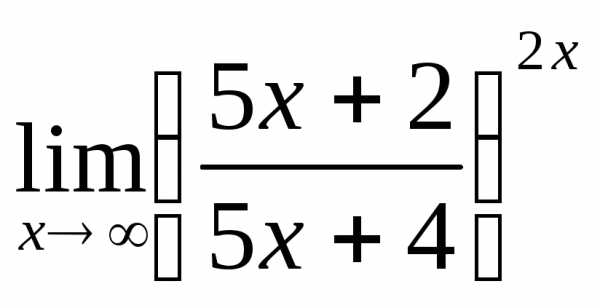 ; в)
; в)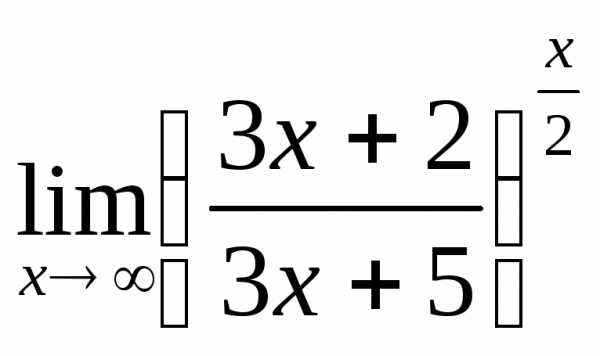 ; г)
; г)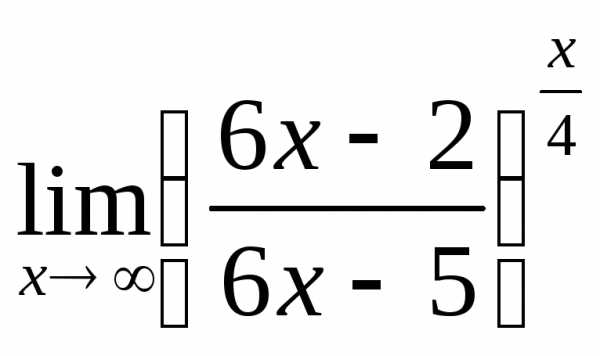 .
.
Пример 27. .
Пример 28.Найдём 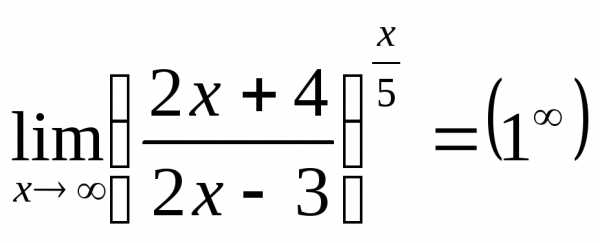 .
Представим основание так:
.
Представим основание так:
(а лучше сразу заметить, что ).
Тогда .
Но .Поэтому .
ПР19. При помощи 2-го замечательного предела
раскройте неопределённость 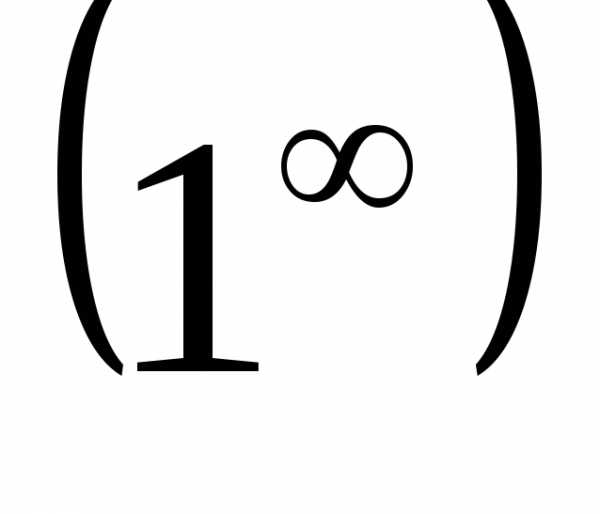 ,
когда аргумент стремится к 0:
,
когда аргумент стремится к 0:
1) а) 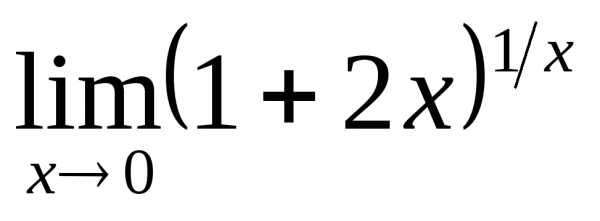 ; б)
; б)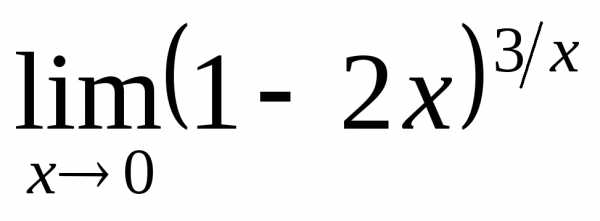 ; в)
; в)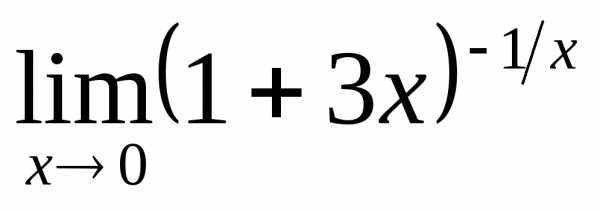 ; г)
; г)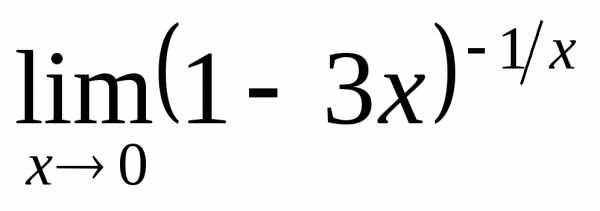 ;
;
2) а) 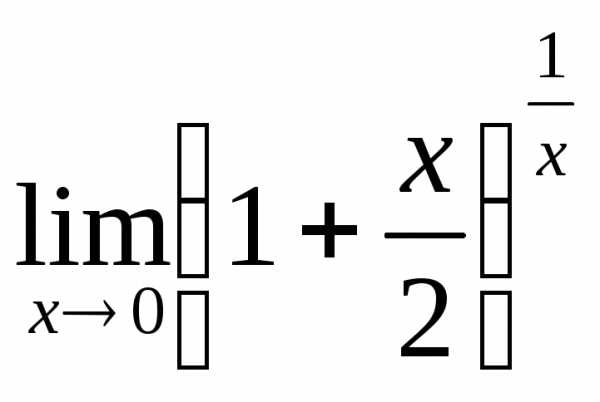 ; б)
; б)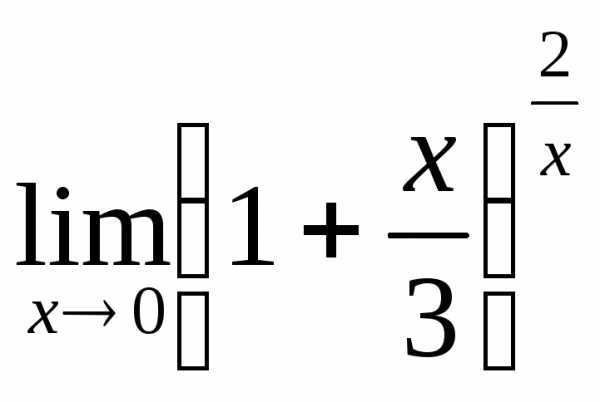 ; в)
; в)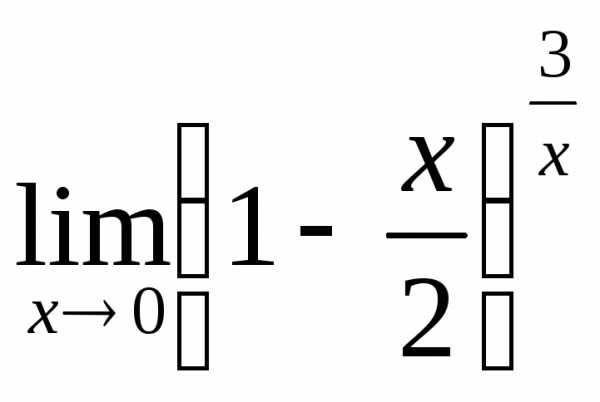 ; г)
; г)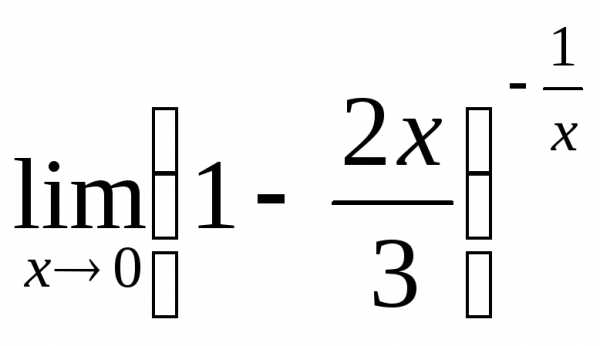 .
.
Пример 29. Преобразовав степень, получаем
а) ;
б) .
ПР20. Найдите пределы
1) а) 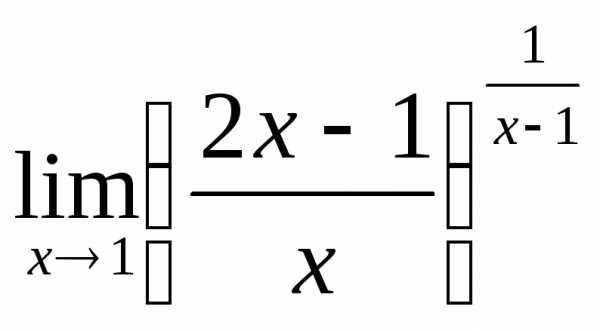 ; б)
; б)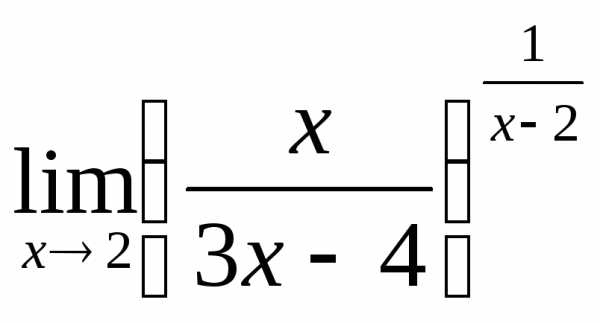 ; в)
; в)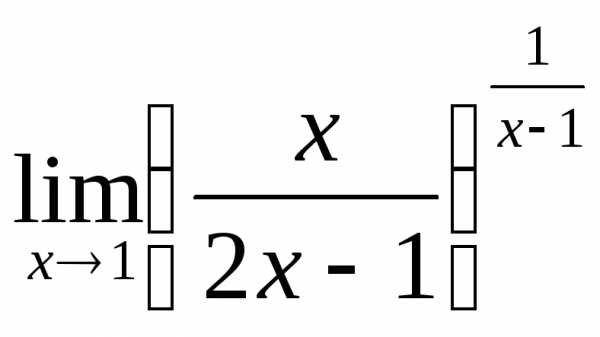 ; г)
; г)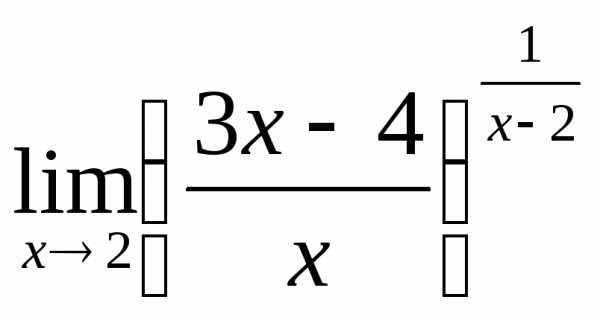 ;
;
2) а) 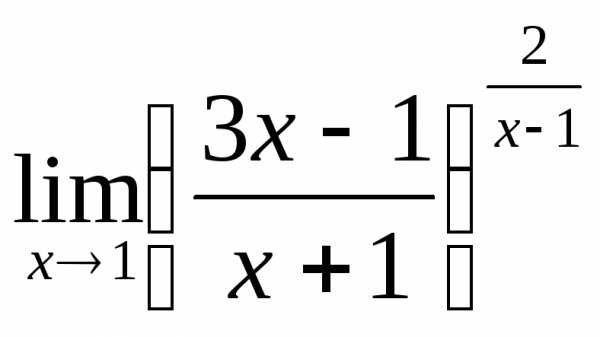 ; б)
; б)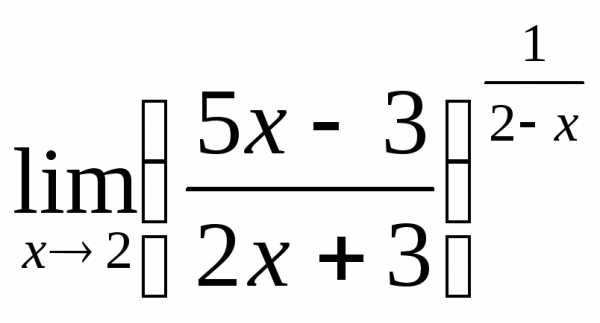 ; в)
; в)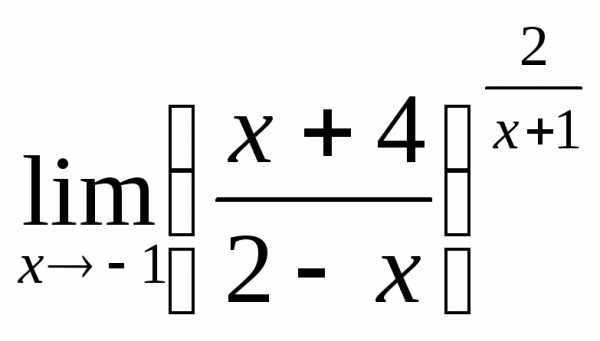 ; г)
; г)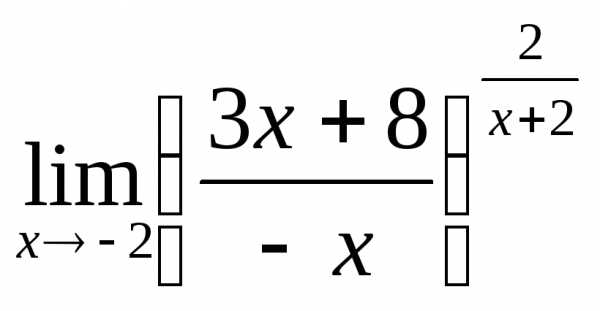 .
.
Пример 30. Найдём . Здесь
,
и тогда
.
В степени присутствует 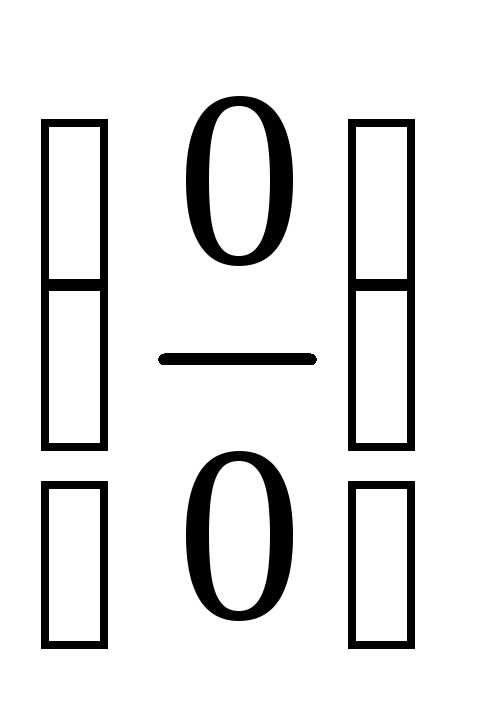 ,
но,
поэтому
,
но,
поэтому
. Это и есть ответ.
Пример 31. Найдём 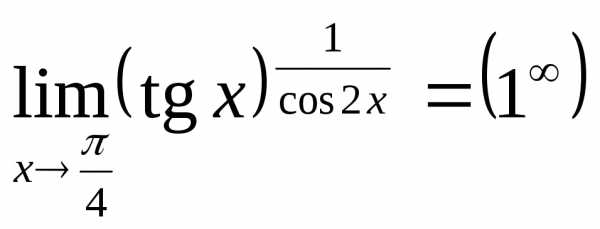 .
Представив,
получаем, что.
.
Представив,
получаем, что.
Теперь находим 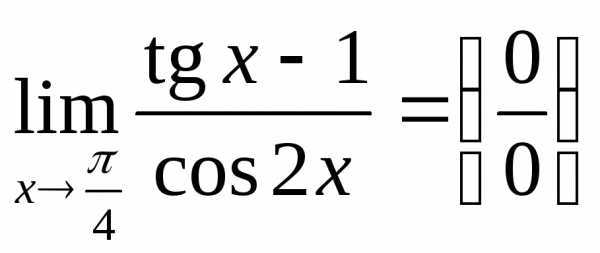 .
Преобразуем показатель степени так:
.
Преобразуем показатель степени так:
.
Тогда
Ответ: 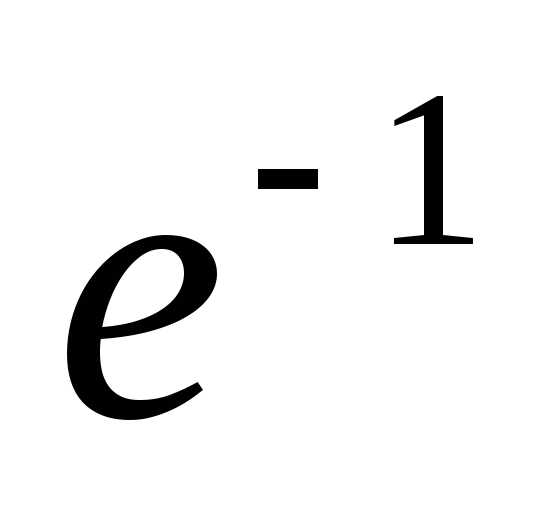 .
.
studfiles.net
Замечательные примеры. Определение и примеры.
В этой статье будут рассмотрены первый и второй замечательные пределы. Мы дадим их определение и разберем на примерах случаи практического применения. Перед прочтением рекомендую сначала ознакомиться с предыдущей статьей о пределах.
Итак, замечательными пределами будем называть тождества вида:
Первый замечательный предел
Как при решении конкретной задачи увидеть и использовать первый замечательный предел? Для этого нужно выяснить, стремится ли к нулю аргумент синуса. Понятно, что далеко не всегда синус будет зависеть именно от . Чаще всего это будут некоторые выражения, но главное, чтобы они обращались в при подстановке предельного значения .
Пример 1. Вычислить предел
Решение: При подстановке предельного значения получаем неопределенность вида . Очевидно, что аргумент синуса стремится к нулю при .
Таким образом, для использования первого замечательно предела нужно получить в знаменателе дроби в точности аргумент синуса . Умножим числитель и знаменатель дроби на :
Предел выражения при равен единице, в соответствии с первым замечательным пределом.
Ответ:
[свернуть]
Пример 2. Вычислить предел
Решение: Подставляем предельное значение , получаем неопределенность вида .
В числителе имеем квадрат синуса, аргумент которого стремится к нулю. Следовательно, удобно будет воспользоваться первым замечательным пределом:
Ответ:
Здесь был дважды применен первый замечательный предел. Мы воспользовались тем фактом, что предел выражения равен при .
[свернуть]
Помимо стандартной формы записи первого замечательно предела, будет справедливо следующее равенство:
Рассмотрим пример с использованием данной модификации.
Пример 3. Вычислить предел
Решение: При подстановке предельного значения получаем неопределенность вида . Аргумент синуса стремится к нулю.
Для использования замечательного предела в числителе дроби должен иметь третью степень. Добьемся этого, умножив числитель и знаменатель дроби на :
Теперь, согласно первому замечательному пределу, вместо выражения можно просто написать :
Ответ:
[свернуть]
Разберем теперь пару примеров, в которых отсутствует синус, но его возможно получить, прибегнув к различным формулам тригонометрии.
Пример 4. Вычислить предел
Решение: При подстановке предельного значения получаем неопределенность вида . Синуса не видно, однако, можно поступить следующим образом: запишем тангенс как отношение синуса к косинусу.
Синус появился и аргумент его стремится к нулю — всё хорошо, можно применять первый замечательный предел:
Ответ:
[свернуть]
Пример 5. Вычислить предел
Решение: При подстановке предельного значения получаем неопределенность вида . Синуса опять не видно. Как его получить, чтобы воспользоваться замечательным пределом? Предлагаю умножить и разделить дробь на :
В числителе появилась формула разности квадратов . У нас есть ее левая часть, то есть , а . Имеем:
Синуса мы не получили, однако в числителе хорошо просматривается основное тригонометрическое тождество . Таким образом, вместо можем смело написать :
Ответ:
[свернуть]
И еще одна задача. Чтобы не было зацикливания на том, что обязательно 🙂
Пример 6. Вычислить предел
Решение: При подстановке предельного значения получаем неопределенность вида .
Как видим, не стремится к нулю, а вот выражение стремится. Для решения такой задачи удобно ввести замену . При этом понятно, что . Получаем:
Синуса нет, но его легко получить, расписав котангенс как отношение косинуса к синусу:
Ответ:
[свернуть]
Второй замечательный предел
Второй замечательный предел служит для избавления от неопределенности вида . Таким образом, если при подстановке предельного значения была получена неопределенность , то сразу понимаем, что предстоит работа именно со вторым замечательным пределом.
Пример 7. Вычислить предел
Решение: Самое первое действие — подставляем предельное выражение . При этом , а всё выражение представляет собой неопределенность .
Наша задача состоит в том, чтобы получить запись вида
Умножим и разделим показатель степени на .
Видим выражение — это второй замечательный предел, заменяем его на букву .
Ответ:
[свернуть]
Замечание. — это иррациональное, равное , то есть приблизительно .
Пример 8. Вычислить предел
Решение: При подстановке предельного значения имеем неопределенность . Если с понимаем этого факта еще возникают сложности, читайте предыдущую статью о пределах.
В основании находится . Следовательно, в показателе степени должно оказаться выражение, обратное к , то есть . Чтобы ничего не изменилось, умножим и разделим показатель на .
Теперь выражение есть второй замечательный предел. Получаем:
Отдельно вычислим предел, обозначенный через :
Возвращаемся к решению исходного предела:
Ответ:
[свернуть]
В обоих разобранных примерах основание степени изначально имело вид «единица плюс выражение от икс». Однако, чаще всего студенту нужно выделить эту единицу самостоятельно:
Пример 10. Вычислить предел
Решение: При подстановке предельного значения получаем . Преобразуем основание степени, дробь, следующим образом:
Вновь мысленно подставляем предельное значение — получаем нашу неопределенность .
Ответ:
[свернуть]
Рассмотрим самую популярную при решении практических задач модификацию второго замечательного предела:
Буквально пару дней назад встретил интересную задачу как раз для этой формулы:
Пример 11. Вычислить предел
Решение: Икс не стремится ни к нулю, ни к бесконечности. Однако, при подстановке предельного значения мы вновь видим неопределенность . Прибавим и отнимем в основании степени единицу:
Теперь в основании появилась единица плюс выражение от икс, стремящееся к нулю. Используем модификацию второго замечательного предела:
В результате получили новый предел, с которым тоже нужно как-то разобраться. При подставке имеем неопределенность вида . Введем замену . При этом понятно, что .
Для тангенса применим формулу тангенса от суммы двух углов. Для косинуса применим формулу приведения.
Возвращаемся к исходному пределу:
Ответ:
[свернуть]
На этом всё. Надеюсь, что статья была полезна.
Удачи в освоении пределов замечательных и не очень! 🙂
higher-math.ru
Второй замечательный предел — МегаЛекции
Первый замечательный предел
Рассмотрим следующий предел:
Согласно нашему правилу нахождения пределов пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида , которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что:
Данный математический факт носит название Первого замечательного предела.
– тот же самый первый замечательный предел.
! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде , то и решать его нужно в таком же виде, ничего не переставляя.
На практике в качестве параметра может выступать не только переменная , но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.
Примеры:
, , ,
Здесь , , , , и всё гуд – первый замечательный предел применим.
А вот следующая запись – ересь:
Почему? Потому-что многочлен не стремится к нулю, он стремится к пятерке.
Кстати, вопрос на засыпку, а чему равен предел ? Ответ можно найти в конце урока.
Переходим к рассмотрению практических примеров:
Пример 1
Найти предел
Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.
Сначала пробуем подставить 0 в выражение под знак предела (делаем это мысленно или на черновике):
Итак, у нас есть неопределенность вида , ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится , а в знаменателе .
В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас , значит, в знаменателе нам тоже нужно получить ».
А делается это очень просто:
То есть, знаменатель искусственно умножается в данном случае на 7 и делится на ту же семерку. Теперь запись у нас приняла знакомые очертания.
Когда задание оформляется от руки, то первый замечательный предел желательно пометить простым карандашом:
Что произошло? По сути, обведенное выражение у нас превратилось в единицу и исчезло в произведении:
Теперь только осталось избавиться от трехэтажности дроби:
Пример 2
Найти предел
Опять мы видим в пределе дробь и синус. Пробуем подставить в числитель и знаменатель ноль:
Действительно, у нас неопределенность и, значит, нужно попытаться организовать первый замечательный предел. мы рассматривали правило, что когда у нас есть неопределенность , то нужно разложить числитель и знаменатель на множители. Здесь – то же самое, степени мы представим в виде произведения (множителей):
Далее, по уже знакомой схеме организовываем первые замечательные пределы. Под синусами у нас , значит, в числителе тоже нужно получить :
Аналогично предыдущему примеру, обводим карандашом замечательные пределы (здесь их два), и указываем, что они стремятся к единице:
Собственно, ответ готов:
Пример 3
Найти предел
Подставляем ноль в выражение под знаком передела:
Получена неопределенность , которую нужно раскрывать. Если в пределе есть тангенс, то почти всегда его превращают в синус и косинус по известной тригонометрической формуле ( В данном случае:
Косинус нуля равен единице, и от него легко избавиться (не забываем пометить, что он стремится к единице):
Таким образом, если в пределе косинус является МНОЖИТЕЛЕМ, то его, грубо говоря, нужно превратить в единицу, которая исчезает в произведении.
Дальше по накатанной схеме, организуем первый замечательный предел:
Здесь все вышло проще, без всяких домножений и делений. Первый замечательный предел тоже превращается в единицу и исчезает в произведении:
В итоге получена бесконечность, бывает и такое.
Пример 4
Найти предел
Пробуем подставить ноль в числитель и знаменатель:
Получена неопределенность (косинус нуля, как мы помним, равен единице)
Используем тригонометрическую формулу . Возьмите на заметку! Пределы с применением этой формулы почему-то встречаются очень часто.
Постоянные множители вынесем за значок предела:
Организуем первый замечательный предел:
Здесь у нас только один замечательный предел, который превращается в единицу и исчезает в произведении:
Избавимся от трехэтажности:
Предел фактически решен, указываем, что оставшийся синус стремится к нулю:
Второй замечательный предел
В теории математического анализа доказано, что:
Данный факт носит название второго замечательного предела.
Справка: – это иррациональное число.
В качестве параметра может выступать не только переменная , но и сложная функция.Важно лишь, чтобы она стремилась к бесконечности.
Пример 6
Найти предел
Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.
Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение , Нетрудно заметить, что при основание степени , а показатель – , то есть имеется, неопределенность вида :
Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр , значит, в показателе нам тоже нужно организовать . Для этого возводим основание в степень , и, чтобы выражение не изменилось – возводим в степень :
Когда задание оформляется от руки, карандашом помечаем:
Практически всё готово, страшная степень превратилась в симпатичную букву :
При этом сам значок предела перемещаем в показатель:
Далее, отметки карандашом я не делаю, принцип оформления, думаю, понятен.
Пример 7
Найти предел
Внимание! Предел подобного типа встречается очень часто, пожалуйста, очень внимательно изучите данный пример.
Пробуем подставить бесконечно большое число в выражение, стоящее под знаком предела:
В результате получена неопределенность . Но второй замечательный предел применим к неопределенности вида . Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас , значит, в числителе тоже нужно организовать :
Теперь можно почленно разделить числитель на знаменатель:
Вроде бы основание стало напоминать , но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:
Таким образом, основание приняло вид , и, более того, появилась нужная нам неопределенность . Организуем второй замечательный предел .
Легко заметить, что в данном примере . Снова исполняем наш искусственный прием: возводим основание степени в , и, чтобы выражение не изменилось – возводим в обратную дробь :
Наконец-то долгожданное устроено, с чистой совестью превращаем его в букву :
Но на этом мучения не закончены, в показателе у нас появилась неопределенность вида , раскрывать такую неопределенность мы научились на уроке Пределы. Примеры решений. Делим числитель и знаменатель на :

Готово.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Первый замечательный предел — Мегаобучалка
Рассмотрим следующий предел: (вместо родной буквы «хэ» я буду использовать греческую букву «альфа», это удобнее с точки зрения подачи материала).
Согласно нашему правилу нахождения пределов (см. статью Пределы. Примеры решений) пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида , которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что:
Данный математический факт носит название Первого замечательного предела.
Нередко в практических заданиях функции могут быть расположены по-другому, это ничего не меняет:
– тот же самый первый замечательный предел.
! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде, то и решать его нужно в таком же виде, ничего не переставляя.
На практике в качестве параметра может выступать не только переменная , но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.
Примеры:
, , ,
Здесь , , , , и всё гуд – первый замечательный предел применим.
А вот следующая запись – ересь:
Почему? Потому-что многочлен не стремится к нулю, он стремится к пятерке.
Кстати, вопрос на засыпку, а чему равен предел ? Ответ можно найти в конце урока.
На практике не все так гладко, почти никогда студенту не предложат решить халявный предел и получить лёгкий зачет. Все-таки «халявные» математические определения и формулы вроде лучше помнить наизусть, это может оказать неоценимую помощь на зачете, когда вопрос будет решаться между «двойкой» и «тройкой», и преподаватель решит задать студенту какой-нибудь простой вопрос или предложить решить простейший пример («а может он (а) все-таки знает чего?!»).
Переходим к рассмотрению практических примеров:
Пример 1
Найти предел
Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.
Сначала пробуем подставить 0 в выражение под знак предела (делаем это мысленно или на черновике):
Итак, у нас есть неопределенность вида , ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится , а в знаменателе .
В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас , значит, в знаменателе нам тоже нужно получить ».
А делается это очень просто:
То есть, знаменатель искусственно умножается в данном случае на 7 и делится на ту же семерку. Теперь запись у нас приняла знакомые очертания.
Когда задание оформляется от руки, то первый замечательный предел желательно пометить простым карандашом:
Что произошло? По сути, обведенное выражение у нас превратилось в единицу и исчезло в произведении:
Теперь только осталось избавиться от трехэтажности дроби:
Готово. Окончательный ответ:
Если не хочется использовать пометки карандашом, то решение можно оформить так:
“
Используем первый замечательный предел
“
Пример 2
Найти предел
Опять мы видим в пределе дробь и синус. Пробуем подставить в числитель и знаменатель ноль:
Действительно, у нас неопределенность и, значит, нужно попытаться организовать первый замечательный предел. На уроке Пределы. Примеры решений мы рассматривали правило, что когда у нас есть неопределенность , то нужно разложить числитель и знаменатель на множители. Здесь – то же самое, степени мы представим в виде произведения (множителей):
Далее, по уже знакомой схеме организовываем первые замечательные пределы. Под синусами у нас , значит, в числителе тоже нужно получить :
Аналогично предыдущему примеру, обводим карандашом замечательные пределы (здесь их два), и указываем, что они стремятся к единице:
Собственно, ответ готов:
В следующих примерах, я не буду заниматься художествами в Пэйнте, думаю, как правильно оформлять решение в тетради – Вам уже понятно.
Пример 3
Найти предел
Подставляем ноль в выражение под знаком передела:
Получена неопределенность , которую нужно раскрывать. Если в пределе есть тангенс, то почти всегда его превращают в синус и косинус по известной тригонометрической формуле (кстати, с котангенсом делают примерно то же самое, см. методический материалГорячие тригонометрические формулы на странице Математические формулы, таблицы и справочные материалы).
В данном случае:
Косинус нуля равен единице, и от него легко избавиться (не забываем пометить, что он стремится к единице):
Таким образом, если в пределе косинус является МНОЖИТЕЛЕМ, то его, грубо говоря, нужно превратить в единицу, которая исчезает в произведении.
Дальше по накатанной схеме, организуем первый замечательный предел:
Здесь все вышло проще, без всяких домножений и делений. Первый замечательный предел тоже превращается в единицу и исчезает в произведении:
В итоге получена бесконечность, бывает и такое.
Пример 4
Найти предел
Пробуем подставить ноль в числитель и знаменатель:
Получена неопределенность (косинус нуля, как мы помним, равен единице)
Используем тригонометрическую формулу . Возьмите на заметку! Пределы с применением этой формулы почему-то встречаются очень часто.
Постоянные множители вынесем за значок предела:
Организуем первый замечательный предел:
Здесь у нас только один замечательный предел, который превращается в единицу и исчезает в произведении:
Избавимся от трехэтажности:
Предел фактически решен, указываем, что оставшийся синус стремится к нулю:
Пример 5
Найти предел
Этот пример сложнее, попробуйте разобраться самостоятельно:

megaobuchalka.ru



