05.04.201912.11.2018

Примеры формула крамера – Метод Крамера для решения СЛАУ: алгоритм, примеры задач

• by alexxlab
• Комментариев к записи Примеры формула крамера – Метод Крамера для решения СЛАУ: алгоритм, примеры задач нет
• Советы абитуриенту

Теорема Крамера, формула и примеры

Пусть задана система уравнений с неизвестными

   

– матрица этой системы, а – столбец свободных членов

   

Если определитель матрицы системы , то системы линейных уравнений (1) имеет единственное решение, которое вычисляется по формулам

   

где – определители матриц, которые получаются из матрицы заменой -го столбца на столбец свободных членов .

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Примеры решений: Метод Крамера

Пример 1. Решить систему уравнений методом Крамера

Решение: 

Составим и вычислим сначала главный определитель этой системы:

Так как , то система имеет единственное решение, которое можно найти по правилу Крамера:

где получаются из определителя путем замены 1-го, 2-го или 3-го столбца, соответственно, на столбец свободных членов.

Таким образом:

Итак, – единственное решение.

 

Пример 2. Решить систему уравнений методом Крамера

Решение: 

Составим главный определитель этой системы:

Используя свойства определителя, создадим в первом столбце нули. Для этого

• Вторую и третью строку оставим без изменеий, 
• Умножим вторую строку на -2 и добавим к первой
• Умножим вторую строку на -1 и добавим к четвертой

После этих преобразований значение определителя не изменится, но он наберет следующий вид

Теперь, воспользовавшись определением определителя и разложив его по элементам четвертого столбца, получим:

 

Итак, главный определитель системы уравнений отличен от нуля. По правилу Крамера такая система имеет единственное решение. Найдем его. Для этого создадим и вычислим еще четыре определители:

 

По правилу Крамера имеем решение:

Итак, – единственное решение.

anet.lectra.me

Формулы Крамера Википедия

Ме́тод Крамера (правило Крамера) — способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы коэффициентов системы (причём для таких уравнений решение существует и единственно).

[1]

Описание метода[ | ]

Для системы n{\displaystyle n} линейных уравнений с n{\displaystyle n} неизвестными (над произвольным полем)

{a11x1+a12x2+…+a1nxn=b1a21x1+a22x2+…+a2nxn=b2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯an1x1+an2x2+…+annxn=bn{\displaystyle {\begin{cases}a_{11}x_{1}+a_{12}x_{2}+\ldots +a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\ldots +a_{2n}x_{n}=b_{2}\\\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\a_{n1}x_{1}+a_{n2}x_{2}+\ldots +a_{nn}x_{n}=b_{n}\\\end{cases}}}

с определителем матрицы системы Δ{\displaystyle \Delta }, отличным от нуля, решение записывается в виде

xi=1Δ|a11…a1,i−1b1a1,i+1…a1na21…a2,i−1b2a2,i+1…a2n…………………an−1,1…an−1,i−1bn−1an−1,i+1…an−1,nan1…an,i−1bnan,i+1…ann|{\displaystyle x_{i}={\frac {1}{\Delta }}{\begin{vmatrix}a_{11}&\ldots &a_{1,i-1}&b_{1}&a_{1,i+1}&\ldots &a_{1n}\\a_{21}&\ldots &a_{2,i-1}&b_{2}&a_{2,i+1}&\ldots &a_{2n}\\\ldots &\ldots &\ldots &\ldots &\ldots &\ldots &\ldots \\a_{n-1,1}&\ldots &a_{n-1,i-1}&b_{n-1}&a_{n-1,i+1}&\ldots &a_{n-1,n}\\a_{n1}&\ldots &a_{n,i-1}&b_{n}&a_{n,i+1}&\ldots &a_{nn}\\\end{vmatrix}}}

(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для

ru-wiki.ru

Формулы Крамера Вики

Ме́тод Крамера (правило Крамера) — способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы коэффициентов системы (причём для таких уравнений решение существует и единственно).

[1]

Описание метода[ | код]

Для системы n{\displaystyle n} линейных уравнений с n{\displaystyle n} неизвестными (над произвольным полем)

{a11x1+a12x2+…+a1nxn=b1a21x1+a22x2+…+a2nxn=b2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯an1x1+an2x2+…+annxn=bn{\displaystyle {\begin{cases}a_{11}x_{1}+a_{12}x_{2}+\ldots +a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\ldots +a_{2n}x_{n}=b_{2}\\\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\a_{n1}x_{1}+a_{n2}x_{2}+\ldots +a_{nn}x_{n}=b_{n}\\\end{cases}}}

с определителем матрицы системы Δ{\displaystyle \Delta }, отличным от нуля, решение записывается в виде

xi=1Δ|a11…a1,i−1b1a1,i+1…a1na21…a2,i−1b2a2,i+1…a2n…………………an−1,1…an−1,i−1bn−1an−1,i+1…an−1,nan1…an,i−1bnan,i+1…ann|{\displaystyle x_{i}={\frac {1}{\Delta }}{\begin{vmatrix}a_{11}&\ldots &a_{1,i-1}&b_{1}&a_{1,i+1}&\ldots &a_{1n}\\a_{21}&\ldots &a_{2,i-1}&b_{2}&a_{2,i+1}&\ldots &a_{2n}\\\ldots &\ldots &\ldots &\ldots &\ldots &\ldots &\ldots \\a_{n-1,1}&\ldots &a_{n-1,i-1}&b_{n-1}&a_{n-1,i+1}&\ldots &a_{n-1,n}\\a_{n1}&\ldots &a_{n,i-1}&b_{n}&a_{n,i+1}&\ldots &a_{nn}\\\end{vmatrix}}}

(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

(c1x1+c2x2+⋯+cnxn)⋅Δ=−|a11a12…a1nb1a21a22…a2nb2……………an1an2…annbnc1c2…cn0|{\displaystyle (c_{1}x_{1}+c_{2}x_{2}+\dots +c_{n}x_{n})\cdot \Delta =-{\begin{vmatrix}a_{11}&a_{12}&\ldots &a_{1n}&b_{1}\\a_{21}&a_{22}&\ldots &a_{2n}&b_{2}\\\ldots &\ldots &\ldots &\ldots &\ldots \\a_{n1}&a_{n2}&\ldots &a_{nn}&b_{n}\\c_{1}&c_{2}&\ldots &c_{n}&0\\\end{vmatrix}}}

В этой форме метод Крамера справедлив без предположения, что Δ{\displaystyle \Delta } отличен от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b1,b2,…,bn{\displaystyle b_{1},b_{2},…,b_{n}} и x1,x2,…,xn{\displaystyle x_{1},x_{2},…,x_{n}}, либо набор c1,c2,…,cn{\displaystyle c_{1},c_{2},…,c_{n}} состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

Пример[ | код]

Система линейных уравнений с вещественными коэффициентами:

{a11x1+a12x2+a13x3=b1a21x1+a22x2+a23x3=b2a31x1+a32x2+a33x3=b3{\displaystyle {\begin{cases}a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+a_{23}x_{3}=b_{2}\\a_{31}x_{1}+a_{32}x_{2}+a_{33}x_{3}=b_{3}\\\end{cases}}}

Определители:

Δ=|a11a12a13a21a22a23a31a32a33|,  Δ1=|b1a12a13b2a22a23b3a32a33|,  {\displaystyle \Delta ={\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{vmatrix}},\ \ \Delta _{1}={\begin{vmatrix}b_{1}&a_{12}&a_{13}\\b_{2}&a_{22}&a_{23}\\b_{3}&a_{32}&a_{33}\\\end{vmatrix}},\ \ }

Δ2=|a11b1a13a21b2a23a31b3a33|,  Δ3=|a11a12b1a21a22b2a31a32b3|{\displaystyle \Delta _{2}={\begin{vmatrix}a_{11}&b_{1}&a_{13}\\a_{21}&b_{2}&a_{23}\\a_{31}&b_{3}&a_{33}\\\end{vmatrix}},\ \ \Delta _{3}={\begin{vmatrix}a_{11}&a_{12}&b_{1}\\a_{21}&a_{22}&b_{2}\\a_{31}&a_{32}&b_{3}\\\end{vmatrix}}}

В определителях столбец коэффициентов при соответствующей неизвестной заменяется столбцом свободных членов системы.

Решение:

x1=Δ1Δ,  x2=Δ2Δ,  x3=Δ3Δ{\displaystyle x_{1}={\frac {\Delta _{1}}{\Delta }},\ \ x_{2}={\frac {\Delta _{2}}{\Delta }},\ \ x_{3}={\frac {\Delta _{3}}{\Delta }}}

Пример:

{2×1+5×2+4×3=30×1+3×2+2×3=1502×1+10×2+9×3=110{\displaystyle {\begin{cases}2x_{1}+5x_{2}+4x_{3}=30\\x_{1}+3x_{2}+2x_{3}=150\\2x_{1}+10x_{2}+9x_{3}=110\\\end{cases}}}

Определители:

Δ=|2541322109|=5,  Δ1=|305415032110109|=−760,  {\displaystyle \Delta ={\begin{vmatrix}2&5&4\\1&3&2\\2&10&9\\\end{vmatrix}}=5,\ \ \Delta _{1}={\begin{vmatrix}30&5&4\\150&3&2\\110&10&9\\\end{vmatrix}}=-760,\ \ }

Δ2=|23041150221109|=1350,  Δ3=|253013150210110|=−1270.{\displaystyle \Delta _{2}={\begin{vmatrix}2&30&4\\1&150&2\\2&110&9\\\end{vmatrix}}=1350,\ \ \Delta _{3}={\begin{vmatrix}2&5&30\\1&3&150\\2&10&110\\\end{vmatrix}}=-1270.}

x1=−7605=−152,  x2=13505=270,  x3=−12705=−254{\displaystyle x_{1}=-{\frac {760}{5}}=-152,\ \ x_{2}={\frac {1350}{5}}=270,\ \ x_{3}=-{\frac {1270}{5}}=-254}

Вычислительная сложность[ | код]

Метод Крамера требует вычисления n+1{\displaystyle n+1} определителей размерности n×n{\displaystyle n\times n}. При использовании метода Гаусса для вычисления определителей метод имеет сложность по элементарным операциям сложения-умножения порядка O(n4){\displaystyle O(n^{4})}, что сложнее, чем метод Гаусса при прямом решении системы. Поэтому метод, с точки зрения затрат времени на вычисления, считался непрактичным. Однако в 2010 году было показано, что метод Крамера может быть реализован со сложностью O(n3){\displaystyle O(n^{3})}, сравнимой со сложностью метода Гаусса

[2].

Литература[ | код]

• Мальцев А. И. Основы линейной алгебры. — Изд. 3-е, перераб., М.: «Наука», 1970. — 400 c.

Примечания[ | код]

1. ↑ Cramer, Gabriel. Introduction à l’Analyse des lignes Courbes algébriques (фр.) 656–659. Geneva: Europeana (1750). Проверено 18 мая 2012.
2. ↑ Ken Habgood and Itamar Arel. 2010. Revisiting Cramer’s rule for solving dense linear systems. In Proceedings of the 2010 Spring Simulation Multiconference (SpringSim ’10)

См. также[ | код]

ru.wikibedia.ru

Метод Крамера, примеры с решением

Одним из методов решения систем линейных уравнений является метод Крамера. Используется для нахождения решения систем, в которых количество строк равно количеству неизвестных. То есть для квадратных систем уравнений. Основан он на вычислении определителей матрицы: основного и дополнительных, получающихся замещением одного из столбца основного определителя на столбец свободных членов системы алгебраических уравнений. Рассмотрим сам алгоритм метода Крамера и примеры с решением.

Дано СЛАУ

Найти неизвестные

Алгоритм решения заключается в том, что  составляется из системы матрица и столбец свободных членов

Далее вычисляется основной определитель матрицы и дополнительные , получающиеся из основного определителя путем поочередного замещения столбцов на столбец свободных членов

Если получается , тогда система не может быть решена методом Крамера! 

В итоге по формуле метода Крамера находим неизвестные в системе линейных уравнений:

Примеры с решением

Пример 1

Решить систему линейных уравнений методом Крамера:

Решение

Составляем матрицу и выписываем столбец свободных членов Вычисляем главный определитель матрицы: Замечаем, что  , то систему можно решить методом Крамера. Вычисляем первый дополнительный определитель  . Подставляем столбец свободных членов  на место первого столбца в основной матрице: Аналогично вычислим : Точно также находим : По формуле Крамера:

Ответ

Пример 2

Решить систему уравнений методом Крамера:

Решение

Попробуем  решить методом Крамера. Найдем основной определитель системы уравнений: Внимание! Получили , а это означает, что данную систему нельзя решить методом Крамера. Алгоритм завершает  свою работу. Советуем воспользоваться другим методом для решения, например, матричным  методом или Гаусса.

Ответ

Метод Крамера нельзя применить к данной системе линейных уравнений

xn--24-6kcaa2awqnc8dd.xn--p1ai

Матричная форма формулы Крамера

С.К. Соболев

Матричный способ решения СЛАУ, формулы Крамера, свойство присоединенной матрицы и основное свойство линейной зависимости.

Рассмотрим систему линейных алгебраических уравнений (СЛАУ ), содержащую
т уравнений и п неизвестных:

(1)

Пусть

– матрица коэффициентов при неизвестных, столбец свободных членов (чисел стоящих справа от равенства в системе (1)) и столбец неизвестных соответственно системы (1). Матрица А называется основной матрицей системы (1). Тогда очевидно, что система (1) может быть кратко записана в матричной форме

. Форма (1) называется координатной записью системы.Если , т.е. число уравнений равно числу неизвестных, то СЛАУ называется «квадратной », она принимает вид: (2)

Если же матрица А к тому же не вырождена, т.е.

, то тогда СЛАУ (2) можно решить как матричное уравнение по формуле . (3)

Этот метод называется матричным способом решения СЛАУ (2).

Пример. Решить систему матричным способом, если это возможно:

Решение . Запишем эту систему как матричное уравнение

, где
, . Вычисляем: , следовательно, матричный способ применим. Находим обратную матрицу:

Следовательно,

.

Ответ:

Формулы Крамера для решения СЛАУ

Эти формулы применимы для решения СЛАУ при тех же условиях, что и матричный способ, а именно, когда матрица А коэффициентов при неизвестных этой СЛАУ квадратная и не вырожденная . Для нахождения неизвестных квадратной системы (2) надо вычислить главный определитель

, убедиться что , и затем вычислить п вспомогательных определителей , где определитель () получается из главного определителя заменой в нем k -го столбца на столбец В свободных членов:

Тогда решением системы (2) будет:

.

Вывод формул Крамера . Распишем подробно формулу (3)

.

Вспомним, что

, где – алгебраическое дополнение элемента , равное , а – определитель порядка , полученный из главного определителя D вычеркиванием i -й строки и j -го столбца. Получим .

Итак, матричный способ дает формулу

(4)

Сравним эту формулу с выражением для

, полученным по формуле Крамера: . (5)

Заметим, что у всех элементов k -го столбца этого определителя алгебраические дополнения точно такие же, как и у элементов k -го столбца матрицы А . Поэтому, разложив определитель в (5) по этому столбцу, получим:

. (6)

Полученная формула (6) в точности совпадает с (4). Формулы Крамера доказаны.

Пример. Решить систему

методом Крамера, если это возможно:

Решение . Вычислим главный определитель системы:

, следовательно, метод Крамера применим. Далее вычислим три вспомогательных определителя:

Следовательно,

.

Дополнение 1. При выводе на лекции в ауд. 220 формулы для обратной матрицы через алгебраические дополнения использовалось основное свойство присоединенной матрицы

.

Доказательство этого свойства, в свою очередь, опиралось на два свойства определителя:

(1) Сумма произведений элементов произвольной строки квадратной матрицы на соответствующие алгебраические дополнения этой же строки равна определителю этой матрицы (и аналогично для столбцов) :

(разложение по i -й строке),
(разложение по j -му столбцу)

(2) Сумма произведений элементов произвольной строки квадратной матрицы на соответствующие алгебраические дополнения другой строки равна нулю (и аналогично для столбцов) :

, (для строк, при ),
(для столбцов, при )

Свойство (1) нам известно из общих свойств определителя, которые у нас идут без доказательства. Среди этих свойств есть, в частности, такое:
если в определителе две строки или два столбца совпадают, то он равен нулю .

Теперь докажем свойство (2). Заменим в определителе

j – строку на строку с номером i . Понятно что после этого у полученного определителя две одинаковые строки, и потому он равен нулю. Заметим также, что алгебраические дополнения изменённой j -й строки не изменились, т.к. они не зависят от элементов этой строки. Разложим определитель по j -й строке, получим:

Аналогично доказывается для столбцов.

Дополнение 2. Относительно линейной зависимости векторов теории линейного пространства, просьба не путать:

Общий критерий линейной зависимости векторов произвольного линейного пространства: Совокупность векторов линейно зависима тогда и только тогда, когда один из векторов выражается в виде линейной комбинации остальных.

Основное свойство линейной зависимости : Пусть даны n векторов линейного пространства , и еще какие-то т векторов этого же пространства, каждый из которых линейно выражается через , причем, . Тогда векторы линейно зависимы .

Доказательство этого свойства есть в лекциях, присланных на вашу Почту.

mirznanii.com

Метод Крамера – вывод формул — Мегаобучалка

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля. В этой статье мы разберем как по методу Крамера находятся неизвестные переменные и получим формулы. После этого перейдем к примерам и подробно опишем решение систем линейных алгебраических уравнений методом Крамера.

При изучении материала Вам может быть полезна статья вычисление определителя матрицы, свойства определителя.

Навигация по странице.

• Метод Крамера – вывод формул.
• Алгоритм решения систем линейных алгебраических уравнений методом Крамера.
• Примеры решения систем линейных алгебраических уравнений методом Крамера.

Метод Крамера – вывод формул.

Пусть нам требуется решить систему линейных уравнений вида

где x₁, x₂, …, x_n – неизвестные переменные, a_{i j} , i = 1, 2, …, n, j = 1, 2, …, n – числовые коэффициенты, b₁, b₂, …, b_n – свободные члены. Решением СЛАУ называется такой набор значений x₁, x₂, …, x_n при которых все уравнения системы обращаются в тождества.

В матричном виде эта система может быть записана как A ⋅ X = B, где – основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных, – матрица – столбец свободных членов, а – матрица – столбец неизвестных переменных. После нахождения неизвестных переменных x₁, x₂, …, x_n, матрица становится решением системы уравнений и равенство A ⋅ X = B обращается в тождество .

Будем считать, что матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера. (Методы решения систем при разобраны в разделе решение систем линейных алгебраических уравнений).

Метод Крамера основывается на двух свойствах определителя матрицы:

1. Определитель квадратной матрицы равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:

2. Сумма произведений элементов какой-либо строки (столбца) квадратной матрицы на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю:

Итак, приступим к нахождению неизвестной переменной x₁. Для этого умножим обе части первого уравнения системы на А_{1 1} , обе части второго уравнения – на А_{2 1} , и так далее, обе части n-ого уравнения – на А_{n 1} (то есть, уравнения системы умножаем на соответствующие алгебраические дополнения первого столбца матрицы А):

Сложим все левые части уравнения системы, сгруппировав слагаемые при неизвестных переменных x₁, x₂, …, x_n, и приравняем эту сумму к сумме всех правых частей уравнений:

Если обратиться к озвученным ранее свойствам определителя, то имеем

и предыдущее равенство примет вид

откуда

Аналогично находим x₂. Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А:

Складываем все уравнения системы, группируем слагаемые при неизвестных переменных x₁, x₂, …, x_n и применяем свойства определителя: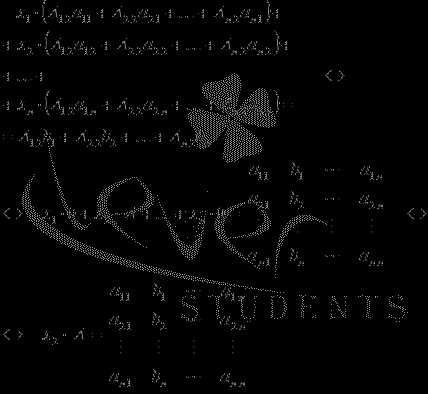

Откуда
.

Аналогично находятся оставшиеся неизвестные переменные.

Если обозначить

то получаем формулы для нахождения неизвестных переменных по методу Крамера .

Замечание.

Если система линейных алгебраических уравнений однородная, то есть , то она имеет лишь тривиальное решение (при ). Действительно, при нулевых свободных членах все определители будут равны нулю, так как будут содержать столбец нулевых элементов. Следовательно, формулы дадут .

К началу страницы

megaobuchalka.ru

---