09.02.202013.11.2018

Сформулируйте закон фарадея – Законы электролиза Фарадея | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

• by alexxlab
• Комментариев к записи Сформулируйте закон фарадея – Законы электролиза Фарадея | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко нет
• Советы абитуриенту

Законы Фарадея в физике

Законы электролиза

При прохождении электрического тока через электролиты происходит процесс разложения вещества, который называют электролизом. При этом проводники, которые погружены в раствор, называют анодом (положительный электрод) и катодом (отрицательный электрод).

При помощи электролиза получают различные вещества, например, хлор, фтор, щелочи и т.д. При помощи данного процесса производят переработку сырья, которое содержит металлы, очищают металлы. Используя процессы электролиза, наносят тонкие металлические покрытия на разные металлические поверхности.

Формулировка первого закона Фарадея

Масса вещества, которое выделяется на электроде, прямо пропорциональна заряду, который прошел через электролит. В виде формулы данный закон можно представить как:

   

где — полный заряд, который проходит через электролит, за времяt. — сила тока. — коэффициент пропорциональности (электрохимический эквивалент вещества ()), равный массе вещества, которая выделится при прохождении через электролит заряда равного 1 Кл. Величина является характеристикой вещества.

Первый закон для электролиза был получен Фарадеем экспериментально.

Формулировка второго закона Фарадея

Электрохимический эквивалент пропорционален молярной массе вещества () и обратно пропорционален величине его химической валентности (). В математическом виде второй закон Фарадея записывают как:

   

где Кл/моль — постоянная Фарадея, полученная эмпирически. Величину называют химическим эквивалентом вещества, она показывает, какая масса вещества требуется для замещения одного моля водорода в химических соединениях.

Иногда второй закон Фарадея формулируют так:

Электрохимические эквиваленты веществ пропорциональны их химическим эквивалентам.

Второй закон Фарадея также относят к эмпирическим законам.

Объединенный закон Фарадея для электролиза

Объединенный закон Фарадея записывают в виде:

   

Физический смысл выражения (3) заключен в том, что постоянная Фарадея количественно равна заряду, который следует пропустить через всякий электролит для того, чтобы на электродах выделилось вещество в количестве, равном одному химическому эквиваленту.

Примеры решения задач

ru.solverbook.com

Закон Фарадея для электромагнитной индукции в трансформаторах

Электричество обладает способностью генерировать магнитное поле. В 1831 году М. Фарадей ввел понятие электромагнитная индукция. Он смог получить в закрытой системе проводников электричество, появляющееся при изменении показателей магнитного потока. Формула закона Фарадея дала толчок для развития электродинамики.

История развития

После доказательства закона электромагнитной индукции английским ученым М. Фарадеем над открытием работали российские ученые Э. Ленц и Б. Якоби. Благодаря их трудам, сегодня разработанный принцип положен в основу функционирования многих приборов и механизмов.

Основными агрегатами, в которых применяется закон электромагнитной индукции Фарадея, являются двигатель, трансформатор и множество иных приборов.

Индукцией электромагнитно именуется индуцирование в замкнутой проводящей системе электрического тока. Такое явление становится возможным при физическом передвижении через проводниковую систему магнитного поля. Механическое действие влечет за собой появление электричества. Его принято называть индукционным. До открытия закона Фарадея человечество не знало об иных способах создания электричества, кроме гальваники.

Если сквозь проводник пропустить магнитное поле, в нем будет возникать ЭДС индукции. Ее еще именуют электродвижущей силой. При помощи этого открытия удается представить в количественном выражении показатель.

Опытное доказательство

Проводя свои исследования, английский ученый установил, что индукционный ток получается одним из двух способов. В первом опыте он появляется при движении рамки в магнитном поле, создаваемом неподвижной катушкой. Второй способ предполагает неподвижное положение рамки. В этом эксперименте изменяется только поле катушки при ее движении или изменении силы тока в ней.

Опыты Фарадея привели исследователя к выводу, что при генерировании индукционного тока провоцируется увеличением или уменьшением магнитного потока в системе. Также опыты Фарадея позволили утверждать, что значение электричества, полученного опытным путем, не зависит от методологии, которой был изменен поток магнитной индукции. На показатель влияет только скорость такого изменения.

Количественное выражение

Установить количественное значение явления электромагнитной индукции позволяет закон Фарадея. Он гласит, что ЭДС, определяющаяся в системе, меняет значение пропорционально скорости перемещения потока в проводнике. Формула будет иметь такой вид:

Отрицательный знак свидетельствует о том, что ЭДС препятствует появлению изменений внутри контура. Для решения некоторых задач отрицательный знак в формуле не ставят. В этом случае результат записывают в виде модуля.

Система может включать в себя несколько витков. Количество их обозначается латинской буквой N. Все элементы контура пронизываются единым магнитным потоком. ЭДС индукции будет рассчитываться так:

Понятным примером воссоздания электричества в проводнике считается катушка, сквозь которую перемещается постоянный магнит.

Работа Э. Ленца

Направленность индукционного тока предоставляет возможность определить правило Ленца. Краткая формулировка звучит достаточно просто. Появляющийся при изменении показателей поля проводникового контура ток, препятствует благодаря своему магнитному полю такому изменению.

Если в катушку постепенно вводить магнит, в ней повышается уровень магнитного потока. Согласно правилу Ленца, магнитное поле будет иметь направление противоположное увеличению поля магнита. Чтобы понять эту направленность, необходимо смотреть на магнит с северной стороны. Отсюда будет вкручиваться буравчик навстречу северному полюсу. Ток будет перемещаться в сторону движения часовой стрелки.

Если магнит выводится из системы, магнитный поток в ней уменьшится. Чтобы установить направление тока, выкручивается буравчик. Вращения будет направлено в обратную сторону перемещения по циферблату часовой стрелки.

Формулировки Ленца приобретают большое значение для системы с контуром замкнутого типа и отсутствующим сопротивлением. Его принято именовать идеальным контуром. По правилу Ленца, в нем невозможно увеличить или уменьшить магнитный поток.

Понятие самоиндукции

Генерация индукции в идеальной системе, которое имеет место при падении или возрастании электричества в проводнике, именуется самоиндукцией.

Закон Фарадея для самоиндукции выражается равенством, когда при изменении электричества не произошло иных изменений:

где е – ЭДС, L – индуктивность закрытой катушки, ΔI/Δt – скорость, с которой происходят изменения силы тока.

Индуктивность

Отношение, которое показывает пропорциональность между такими категориями, как сила тока в проводящей системе и магнитным потоком именуется индуктивностью. На показатель имеет влияние физические габариты катушки и магнитные характеристики среды. Отношение описывается формулой:

Движущееся в контуре электричество провоцирует появление магнитного поля. Оно пронизывает собственный проводник и влечет появление своего потока сквозь контур. Причем собственный поток пропорционален электричеству, которая его порождает:

Фс = L*I

Значение индуктивности также формируется из закона Фарадея.

Недвижимая система

Сила Лоренца объясняет возникновение ЭДС при движении системы в поле со значением постоянным. Индукционная ЭДС имеет способность возникать и при неподвижной проводящей системе, находящейся в переменном магнитном поле. Сила Лоренца в таком примере не способна объяснить появление ЭДС индукции.

Максвелл для проводящих систем неподвижного типа предложил применять особое уравнение. Оно объясняет возникновение в таких системах ЭДС. Главным принципом закона Фарадея-Максвелла является факт, что переменное поле образует в пространстве вокруг себя электрическое поле. Оно выступает фактором, провоцирующим появление тока индукции в недвижимой системе. Перемещение вектора (Е) по стационарным контурам (L) является ЭДС:

При наличии тока переменного значения законы Фарадея водятся в уравнения Максвелла. Причем они могут быть представлены как в дифференциальной форме, так и в виде интегралов.

Труды в области электролиза

При использовании законов Фарадея описываются закономерности, которые существуют при электролизе. Этот процесс заключается в превращении веществ с разнообразными характеристиками. Это происходит при движении электричества сквозь электролит.

Эти закономерности были доказаны М. Фарадеем в 1834 году. Первое утверждение гласит, что масса вещества, которое образуется на электроде, меняется соответственно заряду, перемещенному сквозь электролит.

Второе утверждение гласит, что эквиваленты компонентов с разными характеристиками пропорциональны химическим эквивалентам этих компонентов.

Оба представленных утверждения совмещаются в объединенный закон Фарадея. Из него следует, что число Фарадея будет равняться электричеству, способному выделить на электролите 1 моль вещества. Ее рассчитывают на единицу валентности. Именно по объединенной формуле в далеком 1874 году был вычислен заряд электрона.

Законы электролиза, установленные Фарадеем, тестировались при различном значении тока, температуры, давления, а также при одновременном выделении двух и более веществ. Электролиз также проводился в разных расплавах и растворителях. Концентрация электролита также отличалась в разных опытах. При этом иногда наблюдались небольшие отклонения от закона Фарадея. Они объясняются электронной проводимостью электролитов, которая определяется наравне с ионной проводимостью.

Открытия, сделанные английским физиком М. Фарадеем, позволили описать множество явлений. Его законы являются основой современной электродинамики. По этому принципу функционирует различное современное оборудование.

protransformatory.ru

Законы электролиза Фарадея | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

В 1833 г. М. Фарадей установил:

Масса вещества, которое выделяется при прохож­дении электрического тока в электролитах на аноде или катоде, прямо пропорциональна заряду, который при этом переносится иона­ми через электролит:

m = kq,

где m — масса вещества, кг; q — заряд, Кл.

Коэффициент пропорциональности k = m / q называется электрохимическим эквивален­том данного вещества.

Электрохимический эквивален­т вещества

показывает, какая масса вещества в килограммах выделяется на электроде при прохождении тока, пере­носящего заряд, равный одному кулону:

k = m / q

Если иметь в виду, что при постоянном токе в цепи q = IΔt, где I — сила тока (ам­пер), а Δt — время прохождения тока (се­кунд), то закон Фарадея можно записать в виде

m = kIΔt.

Исходя из современных представлений, закон для электролиза можно установить тео­ретически. Пусть за время Δt через электро­лит переносится заряд q. Заряд одного иона q_0i = ne, где n — валентность иона, а e — значение элементарного электрического заря­да. Следовательно, q = neN_i, где N_i — коли­чество ионов, которые достигли электрода.

С другой стороны, масса вещества, выде­ляющегося на электроде m = m_0iN_i, где m_0i — масса иона, которая может быть определена по молярной массе вещества M и постоян­ной Авогадро N_A:

m_0i = M / N_A; m = (M / N_A) • N_i.

Из уравнения для заряда q = neN_i можно определить N_i: N_i = q / ne. Подставив значения N_iв выражение для массы, получаем:

m = (M / neN_A) • q,

что также является законом Фарадея для электролиза. Итак, электрохимический эквивалент вещества

k = M / neN_A,

где все величины для данного вещества являются постоянными.

В последней формуле значение элемен­тарного заряда e и постоянная Авогадро одинаковы для всех веществ. Их произве­дение назвали постоянной Фарадея:

F = eN_A.

Значение постоянной Фарадея:

F = 1,6 • 10^-19 Кл • 6,023 • 10²³ моль^-1 = -9,65 • 10⁴ Кл/моль.

Теперь для электрохимического эквивалента вещества имеем Материал с сайта http://worldofschool.ru

k = (1 / F) • (M / n),

что и является вторым законом для электролиза.

Второй закон электролиза. Электро­химические эквиваленты веществ прямо про­порциональны массам их молей и обратно пропорциональны их валентностям.

Чтобы удобно было решать многие зада­чи, оба закона можно объединить в одном выражении (объединенный закон электролиза):

m = (1 / F) • (M / n) • q,

или

m = (1 / F) • (M / n) • IΔt.

На этой странице материал по темам:

• Закон электромагнитной индукции фарадея формулировка

• Задачи на законы фарадея для электролиза

• Формула фарадея электролиз

• Формула закона фарадея для электролиза содержащую постоянную фарадея

• Формула и формулировка законов фарадея для электролиза

Вопросы по этому материалу:

• Сформулируйте закон Фарадея для электролиза, запишите его формулу.

• Запишите формулы объединенного закона электролиза.

• Что такое постоянная Фарадея?

worldofschool.ru

Закон индукции Фарадея | энергетик

   Закон индукции Фарадея — Изменение потока магнитной индукции, проходящего через незамкнутую поверхность S, взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре, l который является границей поверхности S.

Таким образом:
Закон Фарадея для электромагнитной индукции — для любого замкнутого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур.

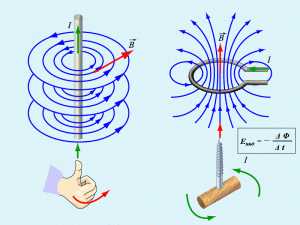
Обозначение в формуле:
B — поток магнитной индукции;
E — электрическое поле;
dL — бесконечно малый элемент контура;
dS — бесконечно малый элемент вектора поверхности.

   Анализируя результаты, полученные опытным путем, Фарадей пришел к количественному закону электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой  электромагнитной индукции. Значение индукционного тока, а, следовательно, и э.д.с. электромагнитной индукции определяется только скоростью изменения магнитного потока, т.е.

   Теперь необходимо выяснить знак e. Вообще, знак магнитного потока зависит от выбора положительной нормали к контуру. В свою очередь, положительное направление нормали определяется правилом правого винта. Следовательно, выбирая положительное направление нормали, мы определяем как знак потока магнитной индукции, так и направление тока и э.д.с. в контуре.

  Пользуясь этими представлениями и выводами, можно соответственно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре э.д.с (обоз. знаком E, ε или e).

   Знак минус показывает, что увеличение потока (dФ/dt>0) вызывает э.д.с  e < 0, т.е. поле индукционного тока направленно навстречу потоку; уменьшение потока (dФ/dt<0) вызывает e > 0, т.е. направление потока и поля индукционного тока совпадают. Знак минус в формуле правилом Ленца — общим правилом для нахождения направления индукционного тока, выведенного в 1833 г.

   Закон Фарадея можно сформулировать еще таким образом: э.д.с. электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром.

   Этот закон является универсальным: э.д.с. не зависит от способа изменения магнитного потока. Э.Д.С. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим:

.

energetik.com.ru

Закон электромагнитной индукции (закон Фарадея) — Мегаобучалка

В результате многочисленных опытов Фарадей установил основной количественный закон электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток. Возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Фарадей установил, что значение ЭДС электромагнитной индукции E_i пропорционально скорости изменения магнитного потока:

 

E_i = -К , (27.1)

 

где К – коэффициент пропорциональности, зависящий только от выбора единиц измерения.

В системе единиц СИ коэффициент К = 1, т.е.

 

E_i = – . (27.2)

 

Эта формула и представляет собой закон электромагнитной индукции Фарадея. Знак минус в этой формуле соответствует правилу (закону) Ленца.

Закон Фарадея можно сформулировать еще таким образом: ЭДС электромагнитной индукции E_i в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: ЭДС E_i не зависит от способа изменения магнитного потока.

Знак минус в (27.2) показывает, что увеличение потока ( > 0) вызывает ЭДС E_i < 0, т.е. магнитный поток индукционного тока направлен навстречу потоку, вызвавшему его; уменьшение потока ( < 0) вызывает E_i > 0 т. е. направления магнитного потока индукционного тока и потока, вызвавшего его, совпадают. Знак минус в формуле (27.2) является математическим выражением правила Ленца – общего правила для нахождения направления индукционного тока (а значит и знака и ЭДС индукции), выведенного в 1833 г. Правило Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Иначе говоря, индукционный ток создает магнитный поток, препятствующий изменению магнитного потока, вызывающего ЭДС индукции.

ЭДС индукции выражается в вольтах (В). Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим:

 

.

 

Если замкнутый контур, в котором индуцируется ЭДС индукции, состоит из N витков, то E_i будет равна сумме ЭДС, индуцируемых в каждом из витков. И если магнитный поток, охватываемый каждым витком, одинаков и равен Ф, то суммарный поток сквозь поверхность N витков, равен (NФ) – полный магнитный поток (потокосцепление). В этом случае ЭДС индукции равна:

 

E_i = -N× , (27.3)

 

Формула (27.2) выражает закон электромагнитной индукции в общей форме. Она применима как к неподвижным контурам, так и к движущимся проводникам в магнитном поле. Входящая в нее производная от магнитного потока по времени в общем случае состоит из двух частей, одна из которых обусловлена изменением магнитной индукции во времени, а другая – движением контура относительно магнитного поля (или его деформацией). Рассмотрим некоторые примеры применения этого закона.

Пример 1. Прямолинейный проводник длиной l движется параллельно самому себе в однородном магнитном поле (рисунок 38). Этот проводник может входить в состав замкнутой цепи, остальные части которой неподвижны. Найдем ЭДС, возникающую в проводнике.

Если мгновенное значение скорости проводника есть v, то за время dt он опишет площадь dS = l×v×dt и за это время пересечет все линии магнитной индукции, проходящие через dS. Поэтому изменение магнитного потока через контур, в состав которого входит движущийся проводник, будет dФ = B_n×l×v×dt. Здесь B_n – составляющая магнитной индукции, перпендикулярная к dS. Подставляя это в формулу (27.2) получаем величину ЭДС:

 

E_i = B_n×l×v. (27.4)

 

Направление индукционного тока и знак ЭДС определяются правилом Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток. В некоторых случаях возможно определение направления индукционного тока (полярности ЭДС индукции) согласно другой формулировке правила Ленца: индукционный ток в движущемся проводнике направлен таким образом, что возникающая при этом сила Ампера противоположна вектору скорости (тормозит движение).

Разберем численный пример. Вертикальный проводник (автомобильная антенна) длиной l = 2 м движется с востока на запад в магнитном поле Земли со скоростью v = 72 км/час = 20 м/с. Вычислим напряжение между концами проводника. Так как проводник разомкнут, то тока в нем не будет и напряжение на концах будет равно ЭДС индукции. Учитывая, что горизонтальная составляющая магнитной индукции поля Земли (т.е. составляющая, перпендикулярная к направлению движения) для средних широт равна 2×10^-5 Тл, по формуле (27.4) находим

 

U = B_n×l×v = 2×10^-5×2×20 = 0,8×10^-3 В,

 

т.е. около 1 мВ. Магнитное поле Земли направлено с юга на север. Поэтому мы находим, что ЭДС направлена сверху вниз. Это значит, что нижний конец провода будет иметь более высокий потенциал (зарядится положительно), а верхний – более низкий (зарядится отрицательно).

Пример 2. В магнитном поле находится замкнутый проволочный контур, пронизываемый магнитным потоком Ф. Предположим, что этот поток уменьшается до нуля, и вычислим полную величину заряда, прошедшего по цепи. Мгновенное значение ЭДС в процессе исчезновения магнитного потока выражается формулой (27.2). Следовательно, согласно закону Ома мгновенное значение силы тока есть

 

I = – , (27.5)

 

где R – полное сопротивление цепи.

Величина прошедшего заряда равна

 

q = = – = . (27.6)

 

Полученное соотношение выражает закон электромагнитной индукции в форме, найденной Фарадеем, который из своих опытов заключил, что величина заряда, прошедшего по цепи, пропорциональна полному числу линий магнитной индукции, пересеченных проводником (т.е. изменению магнитного потока Ф₁-Ф₂), и обратно пропорциональна сопротивлению цепи R. Соотношение (27.6) позволяет дать определение единицы магнитного потока в системе СИ: вебер – магнитный поток, при убывании которого до нуля в сцепленном с ним контуре сопротивлением 1 Ом проходит заряд 1 Кл.

Согласно закону Фарадея, возникновение ЭДС электромагнитной индукции возможно и в случае неподвижного контура, находящегося в переменном магнитном поле. Однако сила Лоренца на неподвижные заряды не действует, поэтому в данном случае она не может быть причиной возникновения ЭДС индукции. Максвелл для объяснения ЭДС индукции в неподвижных проводниках предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция вектора напряженности этого поля по любому неподвижному контуру L проводника представляет собой ЭДС электромагнитной индукции:

 

E_i = = – . (27.7)

 

Линии напряженности вихревого электрического поля представляют собой замкнутые кривые, поэтому при перемещении заряда в вихревом электрическом поле по замкнутому контуру совершается отличная от нуля работа. В этом заключается отличие вихревого электрического поля от электростатического, линии напряженности которого начинаются и заканчиваются на зарядах.

megaobuchalka.ru

Законы Фарадея

Количественные закономерности электролита установил английский физик М. Фарадей. Эти закономерности нетрудно вывести теоретически на основе представления об ионной проводимости.

Если за время у электрода нейтрализуетсяионов, каждый из которых имеет валентностьи массу, то электрод получит заряд

,

где – заряд электрона. При этом на электроде осядет масса вещества.

Отношение

(8)

есть постоянная для данного вещества величина, называемая электрохимическим эквивалентом этого вещества. Очевидно, что электрохимический эквивалент равен количеству вещества, выделяющегося на электроде при прохождении через раствор единицы количества электричества. Из формулы (8) следует, что

,

где – сила тока, протекающего через раствор.

Первый закон Фарадея. Масса вещества, выделяющегося на электроде пропорциональна количеству электричества, прошедшего через раствор.

Умножим и разделим (8) на постоянную Авогадро :

.

Учитывая, что – молярная масса вещества, получим

,

где

– универсальная постоянная, называемая постоянной Фарадея. Отношение называетсяхимическим эквивалентом вещества.

Второй закон Фарадея. Электрохимический эквивалент вещества пропорционален его химическому эквиваленту.

Объединив оба закона Фарадея, получим

,

откуда следует, что при, т. е. постоянная Фарадея равна количеству электричества, при прохождении которого через раствор на каждом из электродов выделяется количество вещества, равное химическому эквиваленту.

Согласно опытным данным,

39. Магнитное поле при наличии магнетиков. Поле элементарного тока. Магнитный момент элементарного тока. Механизмы намагничивания. Напряженность магнитного поля. Граничные условия для векторов магнитного поля.

Движущийся по орбите электрон обладает механическим моментом импульса , модуль которого

,

где ,. Вектор(его направление определяется по правилу правого винта) называется орбитальным механическим моментом электрона. Направленияипротивоположны, поэтому

,

где величина

называется гиромагнитным отношением орбитальных моментов (общепринято писать со знаком “-”, указывающим на то, что направления моментов противоположны). Это отношение, определяемое универсальными постоянными, одинаково для любой орбиты, хотя для разных орбит значения иразличны.

Аналогично электрон обладает собственным механическим моментом импульса , называемый спином. Считалось, что спин обусловлен вращением электрона вокруг своей оси, что привело к целому ряду противоречий. Спину электрона соответствует собственный (спиновой) магнитный момент, пропорциональныйи направленный в противоположную сторону:

.

Величина называется гиромагнитным отношением спиновых моментов.

Проекция собственного магнитного момента на направление вектора может принимать только одно из следующих значений:

,

где ,- магнетон Бора, являющийся единицей магнитного момента электрона.

Всякое вещество является магнетиком, т.е. оно способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Для понимания механизма этого явления необходимо рассмотреть действие магнитного поля на движущиеся в атоме электроны.

Ради простоты предположим, что электрон в атоме движется по круговой орбите. Если орбита электрона ориентирована относительно вектора произвольным образом, составляя с ним угол, то можно доказать, что она приходит в такое движение вокруг, при котором вектор магнитного момента, сохраняя постоянным угол, вращается вокруг векторас некоторой угловой скоростью. Такое движение называется прецессией.

Таким образом, электронные орбиты атома под действием внешнего магнитного поля совершают прецессионное движение, которое эквивалентно круговому току. Так как этот микроток индуцирован внешним магнитным полем, то, согласно правилу Ленца, у атома появляется составляющая магнитного поля, направленная противоположно внешнему полю. Наведенные составляющие магнитных полей атомов (молекул) складываются и образуют собственное магнитное поле вещества, ослабляющее внешнее магнитное поле. Этот эффект получил название диамагнитного эффекта, а веществ, намагничивающиеся во внешнем магнитном поле против направления поля, называются диамагнетиками.

В отсутствие внешнего магнитного поля диамагнетик немагнитен, поскольку в данном случае магнитные моменты электронов взаимно компенсируются, и суммарный магнитный момент атома равен нулю. К диамагнетикам относятся многие металлы, большинство органических соединений, смолы, углерод и т.д.

Так диамагнитный момент эффект обусловлен действием внешнего магнитного поля на электроны атомов вещества, то диамагнетизм свойствен всем веществам. Однако наряду с диамагнитными веществами существуют и парамагнитные – вещества, намагничивающиеся во внешнем магнитном поле по направлению поля.

У парамагнитных веществ при отсутствии внешнего поля магнитные моменты электронов не компенсируют друг друга, и атомы парамагнетиков всегда обладают магнитным моментом. Однако вследствие теплового движения молекул их магнитные моменты ориентированы беспорядочно, поэтому парамагнитные вещества магнитными свойствами не обладают. При внесении парамагнетика во внешнее магнитное поле устанавливается преимущественная ориентация магнитных атомов по полю (полной ориентации препятствует тепловое движение атомов). Таким образом, парамагнетик намагничивается, создавая собственное магнитное поле, совпадающее по направлению с внешним полем и усиливающее его. Этот эффект называется парамагнитным. При ослаблении внешнего магнитного пол до нуля ориентация магнитных моментов вследствие теплового движения нарушается и парамагнетик размагничивается. Диамагнитный момент наблюдается и у парамагнетиков, но он значительно слабее парамагнитного и поэтому остается незаметным.

Также для определения вида магнетика проводят следующий опыт: 1 грамм исследуемого вещества помещают в поле (Гс – единица магнитного поля в ГДС). Диамагнетики выталкиваются магнитным полем. Например, вода (сила – -22 дины), свинец (сила – -37 дин), медь (сила – -2.6 дин). Парамагнетики втягиваются полем. Например,Al +17 дин, жидкий +20 дин,Fe +400000 дин, магнетит +120000 дин.

Намагниченность. Магнитное поле в веществе.

Для количественного описания намагничения магнетиков вводят векторную величину – намагниченность, определяемую магнитным моментом единицы объема магнетика:

,

где – магнитный момент магнетика, представляющий собой векторную сумму магнитных моментов отдельных молекул.

Магнитное поле в веществе складывается из двух полей: внешнего поля, создаваемого током, и поля, создаваемого намагниченным веществом. Тогда можем записать, что вектор магнитной индукции результирующего магнитного поля в магнетике равен векторной сумме магнитных индукций внешнего поля (поля, создаваемого намагничивающим током в вакууме) и поля микротоков(поля, создаваемого молекулярными токами):

,

где . Так как- вектор намагниченности, и для изотропных магнетиков, где- магнитная восприимчивость.

,

здесь – относительная магнитная проницаемость, показывающая, во сколько раз индукция магнитного поля в окружающей среде отличается от индукции в вакууме. Для диамагнетика, для парамагнетика.

Электронный парамагнитный резонанс используется для определения величины . В определенном объеме – резонаторе – находится исследуемое вещество. Образец перемагничивают с частотой, он помещен в магнитное поле. Наблюдают поглощение энергии, которое максимально, если.

Граничные условия:

Рассмотрим границу двух однородных изотропных магнетиков , вдоль которой течет поверхностный ток проводимости с линейной плотностью . Пусть система находится в однородном магнитном поле. Используем теорему о полном магнитном потоке и теорему о циркуляции вектора напряженностии.

Рассмотрим на границе замкнутую поверхность в виде прямого цилиндра с (рис.101). Поток вектора магнитной индукции в этом случае:или, т.е. нормальная составляющая вектора магнитной индукции одинакова в обоих магнетиках. Так как, то.

Применим теорему о циркуляции вектора напряженности к очень малому прямоугольному контуру. Пусть вектор линейной плотности тока совпадает с нормалью к контуру (рис.102).

Так как контур очень узкий, то вклад в циркуляцию на боковых сторонах очень мал. Тогда: , т.е. тангенциальная составляющая вектора напряженности, а следовательно и вектора магнитной индукции на границе раздела претерпевает скачок, обусловленный наличием поверхностных токов проводимости.

Если на границе раздела магнетиков токов проводимости нет, то и, соответственно,. На границе раздела двух магнетиков линии вектора индукции испытывают преломление, но непрерывны.

Линии вектора напряженности преломляются по такому же закону, но терпят разрыв из-за поверхностных токов намагничивания (даже в отсутствие токов проводимости).

На рис. 103 представлены линии векторов индукции и напряженности для случая >.

На этом основана магнитная защита, т.е. использование замкнутой железной оболочки для защиты внутреннего пространства от внешнего магнитного поля. Линии поля концентрируются в самой оболочке, а в окруженном оболочкой пространстве магнитное поле значительно меньшей величины, чем внешнее поле.

studfiles.net

Первый и второй закон Фарадея

 

Электролит всегда имеет определённое количество ионов со знаками “плюс” и “минус”, получившихся в результате взаимодействия молекул растворённого вещества с растворителем. Когда в нем возникает электрическое поле, ионы начинают двигаться к электродам, положительные устремляются к катоду, отрицательные – к аноду. Дойдя до электродов, ионы отдают им свои заряды, превращаются в нейтральные атомы и отлагаются на электродах. Чем больше ионов подойдёт к электродам, тем больше будет отложено на них вещества.

К этому заключению мы можем прийти и опытным путём. Пропустим ток через водный раствор медного купороса и будем наблюдать за выделением меди на угольном катоде. Мы обнаружим, что вначале он покроется едва заметным слоем меди, затем по мере пропускания тока он будет увеличиваться, а при долговременном пропускании тока можно получить на угольном электроде значительной толщины слой меди, к которому легко припаять, например, медный провод.

Явление выделения вещества на электродах во время прохождения тока сквозь электролит называется электролизом.

Пропуская через разные электролизы различные токи и тщательно измеряя массу вещества, выделяющегося на электродах из каждого электролита, английский физик Фарадей в 1833 – 1834 гг. открыл два закона для электролиза.

Первый закон Фарадея устанавливает зависимость между массой выделившегося вещества при электролизе и величиной заряда, который прошел через электролит.

Закон этот формулируется следующим образом: масса вещества, которая выделилась при электролизе, на каждом электроде прямо пропорциональна величине заряда, который прошел сквозь электролит:

m=kq,

где m – масса вещества, которое выделилось, q – заряд.

Величина k – электрохимическимй эквивалент вещества. Она характерна для каждого вещества, выделяющегося при электролите.

Если в формуле принять q = 1 кулону, тогда k = m, т.е. электрохимический эквивалент вещества будет численно равняться массе вещества, выделенного из электролита при прохождении заряда в один кулон.

Выражая в формуле заряд через ток I и время t, получим:

m=kIt.

Первый закон Фарадея проверяется на опыте следующим образом. Пропустим ток через электролиты А, В и С. Если все они одинаковые, то массы выделенного вещества в А, В и С будут относиться как токи I, I1, I2. При этом количество вещества, выделенного в А, будет равно сумме объемов, выделенных в В и С, так как ток I= I1+ I2.

Второй закон Фарадея устанавливает зависимость электрохимического эквивалента от атомного веса вещества и его валентности и формулируется следующим образом: электрохимический эквивалент вещества будет пропорционален их атомному весу, а также обратно пропорционален его валентности.

Отношение атомного веса вещества к его валентности называется химическим эквивалентом вещества. Введя эту величину, второй закон Фарадея сформулировать можно иначе: электрохимические эквиваленты вещества пропорциональны их собственным химическим эквивалентам.

Пусть электрохимические эквиваленты разных веществ соответственно равны k1 и k2, k3, …, kn, химические же эквиваленты тех же веществ x1 и x2, x23, …, xn, тогда k1 /k2 = x1 /x2, или k1/x1 = k2/x2 = k3/ x3 = … = kn/ xn.

Иначе говоря, отношение величины электрохимического эквивалента вещества к величине того же вещества есть величина постоянная, имеющая для всех веществ одно и то же значение:

k/x=c.

Отсюда следует, что отношение k/x является постоянным для всех веществ:

k/x=c = 0, 01036 (мг-экв)/к.

Величина с показывает, сколько миллиграмм-эквивалентов вещества выделяется на электродах во время прохождения через электролит электрического заряда, равно 1 кулону. Второй закон Фарадея представлен формулой:

k=cx.

Подставляя полученное выражение для k в первый закон Фарадея, оба можно объединить в одном выражении:

m= kq=cxq=cxIt,

где с – универсальная постоянная, равная 0, 00001036 (г-экв)/к.

Эта формула показывает, что, пропуская одинаковые токи в течение одного и того же промежутка времени через два различных электролита, мы выделим из обоих электролитов количества веществ, относящихся как химические эквиваленты таковых.

Так как x=A/n, то можно написать:

m=cA/nIt,

т.е., масса вещества, выделенного на электродах при электролизе, будет прямо пропорциональна его атомному весу, току, времени и обратно пропорциональна валентности.

Второй закон Фарадея для электролиза, так же, как и первый, непосредственно вытекает из ионного характера тока в растворе.

Закон Фарадея, Ленца, а также многих других выдающихся физиков сыграл огромную роль в истории становления и развития физики.

fb.ru

---