Вычислить пределы не пользуясь правилом лопиталя – Вычисление пределов, без использования правила Лопиталя.
- Комментариев к записи Вычислить пределы не пользуясь правилом лопиталя – Вычисление пределов, без использования правила Лопиталя. нет
- Советы абитуриенту
- Найти пределы функций, не пользуясь правилом Лопиталя
- Найти пределы функций, не пользуясь правилом Лопиталя — Мегаобучалка
- 1. Найти указанные пределы, не пользуясь правилом Лопиталя
- Вычислить пределы используя правило лопиталя — Адвокатский клуб
- Правило Лопиталя
- Введите функцию и точку для предела, которому надо применить правило Лопиталя
- Нахождение предела функции в точке по правилу Лопиталя
- пределы — Вычислить предел используя правило Лопиталя:
- Правило Лопиталя: теория и примеры решений
- Правило Лопиталя и раскрытие неопределённостей
- Раскрытие неопределённостей видов «ноль делить на ноль» и «бесконечность делить на бесконечность»
- Раскрытие неопределённостей вида «ноль умножить на бесконечность»
- Раскрытие неопределённостей видов «ноль в степени ноль», «бесконечность в степени ноль» и «один в степени бесконечность»
- Раскрытие неопределённостей вида «бесконечность минус бесконечность»
- Правило Лопиталя с примерами
Найти пределы функций, не пользуясь правилом Лопиталя
Задача №1
Зависимости координат от времени при движении материальной точки в плоскости
и имеют вид:Определить модуль скорость (
) и ускорение () этой точки в момент времени .Решение
А. Модуль скорости материальной точки от времени выражается по формуле:
Следовательно,
Б. . Модуль ускорения материальной точки от времени выражается по формуле:
Данные уравнения описывают движение материальной точки с постоянным ускорением
.Задача №2
Спутник вращается вокруг земли по круговой орбите на высоте
. Определите линейную и угловую скорости спутника. Ускорение свободного падения у поверхности Земли . Радиус ЗемлиРешение
На спутник, движущийся по круговой орбите, действует сила тяжести
, которая во много раз превосходит силы тяготения, действующие на него со стороны других небесных тел, поэтому по второму закону Ньютона . Здесь — масса спутника, его центростремительное ускорение. По закону всемирного тяготения . Здесь — гравитационная постоянная, — расстояние от спутника до центра Земли, т.е. радиус круговой орбиты спутника (), — масса Земли. Центростремительное ускорение спутника связано с линейной скоростью спутника соотношением или . Следовательно, получаем уравнение движения спутника на высоте : илиТаким образом, линейная скорость спутника равна
,а угловая скорость
Задача №3
Шар массой
движется со скоростью и сталкивается с покоящимся шаром массой и скоростью . Определить скорости шаров и после удара, если он абсолютно упругий, прямой, центральный.Решение
Рассматриваемые в задаче оба шара образуют замкнутую систему и в случае упругого удара и импульс системы, и механическая (кинетическая) энергия сохраняется. Запишем оба закона сохранения (с учётом неподвижности второго шара до удара):
Таким образом, налетающий (первый) шар в результате удара уменьшил свою скорость с 1,05 м/с до 0,45 м/с, хотя и продолжил движение в прежнем направлении, а ранее неподвижный (второй) шар приобрёл скорость, равную 1,5 м/с и теперь оба шара движутся по одной прямой, и в одном направлении.
Задача №4
Баллон вместимостью
наполнен азотом при температуре . Когда часть газа израсходовалась давление понизилось на . Определить массу израсходованного газа. Процесс считать изотермическим (при постоянной температуре).Решение
Пусть
— молярная масса азота; — начальная и конечная масса газа; — расход газа. — начальное и конечное давление газа в баллоне; — снижение давления газа; — универсальная газовая постоянная.Так как масса газа в баллоне меняется, то начальное и конечное состояния газа в баллоне нельзя связывать ни законом Бойля-Мариотта, ни законом Шарля.равнением газа в баллоне меняется, то начальное и конечное состояния газа в баллоне нельзя связывать законом Бойля-Мариотт Нужно для каждого состояния записать уравнение Менделеева-Клапейрона
Задача №5
Вычислить плотность азота
, находящегося в баллоне под давлением и имеющего температуру .Решение
Пусть
— молярная масса азота; — универсальная газовая постоянная; — давление газа в баллоне; — температура газа в баллоне.Запишем уравнение Менделеева-Клапейрона для текущего состояния газа (с учётом, что
): .mirznanii.com
Найти пределы функций, не пользуясь правилом Лопиталя — Мегаобучалка
Математика
КОНТРОЛЬНЫЕ ЗАДАНИЯ
(с краткими методическими указаниями)
для студентов заочной формы обучения
специальности 23.02.01 «Организация перевозок и управление на транспорте (по видам)»
Артем
Общие рекомендации по изучению дисциплины
Предполагается, что главной формой обучения студента – заочника является самостоятельное изучение дисциплины. При изучении дисциплины предлагаем руководствоваться следующими рекомендациями:
· изучить теоретический материал по очередной теме;
· внимательно проанализировать примеры решения типовых задач графические иллюстрации к ним;
· решить соответствующую задачу из контрольной работы, возвращаясь, если необходимо, к теоретическому материалу.
Общие указания по выполнению и оформлению контрольной работы
При выполнении контрольных работ предлагаем руководствоваться следующими рекомендациями:
· Контрольную работу следует выполнять в отдельной тетради (в клетку), чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
· На внешней обложке тетради должно быть ясно написаны фамилия студента, его инициалы, полный шифр, дата отсылки контрольной работы в колледж, домашний адрес студента. В конце работы следует проставить дату ее выполнения и расписаться.
· В работу должны быть включены все задачи, указанные в задании. Работы, содержащие не все задачи, а также задачи не своего варианта, не рецензируются.
· Решение задач следует располагать в порядке номеров указанных в заданиях, сохраняя номера задач.
· Перед решением каждой задачи надо полностью переписать ее условие.
· Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения.
· Решение задач геометрического содержания должно сопровождаться чертежами, выполненными аккуратно, с указанием осей координат и единиц масштаба. Объяснения к задачам должно соответствовать обозначениям, приведенным на чертеже.
· Контрольная работа должна выполняться самостоятельно. Несамостоятельно выполненная работа лишает студента возможности проверить степень своей подготовленности по теме. Если преподаватель установит несамостоятельное выполнение работы, то она не будет зачтена.
· Получив из колледжа прорецензированную работу, студент должен исправить все отмеченные рецензентом ошибки и недочеты. Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует в короткий срок. В случае не зачета работы, вся работа должна быть выполнена заново.
· Номер варианта соответствует первой букве фамилии, согласно ниже приведенной таблице.
| А, Ш, Ч | Б, Э, П | В, Я, Н | Г, У, О | Д, Р | Е, М, Ц | Ж, С | З, Х, Т | К, И Ю | Л, Ф Щ |
КОНТРОЛЬНАЯ РАБОТА
Найти пределы функций, не пользуясь правилом Лопиталя.
1. а) ; б) ; в) ; г) .
2 .а) ; б) ; в) ; г) .
3. а) ; б) ; в) ; г) .
4. а) ; б) ; в) ; г) .
5. а) ; б) ; в) ; г) .
6. а) ; б) ; в) ; г) .
7. а) ; б) ; в) ; г) .
8. а) ; б) ; в) ; г) .
9. а) ; б) ; в) ; г) .
10. а) ; б) ; в) ; г) .
megaobuchalka.ru
1. Найти указанные пределы, не пользуясь правилом Лопиталя
1. Найти указанные пределы, не пользуясь правилом Лопиталя.а) .
b) .
с)
d)
e)
2. Найти производные данных функций.
a)
b)
c)
d)
e)
Продифференцируем данное выражение по x, помня, что y=y(x):
Выразим y’:
где y определяется выражением .
f)
Пусть
, тогда
Получаем
3. С помощью правила Лопиталя вычислить пределы.
a)
b)
4. Исследовать методами дифференциального исчисления следующие функции и построить их графики.
a)
Область определения:
, функция ни чётная, ни нечётная (общего вида).
Непериодическая.
Точки пересечения с осями.
С осью OX: при , .
точка пересечения ; .
С осью ОY: при.
точка пересечения .
Асимптоты.
а) Вертикальных асимптот нет.
6) Ищем наклонные асимптоты в виде y=kx+b.
Значит, наклонных асимптот нет.
Экстремумы функции:
.
Т. к. при , , а при , , то – точка минимума.
На отрезке – функция убывает.
На отрезке – функция возрастает.
Точки перегиба графика функции
Т. к. при , , а при , , то и– точки перегиба.
При функция выпукла вниз.
При функция выпукла вверх.
На основании полученных данных построим график.
b)
Область определения:
, функция нечётная, график симметричен относительно начала координат.
Непериодическая.
Точки пересечения с осями.
С осью OX: при , , следовательно, точек пересечения нет.
С осью ОY точек пересечения нет.
Асимптоты.
а) Вертикальные асимптоты.
x=0 – вертикальная асимптота графика.
б) Ищем наклонные асимптоты в виде y=kx+b.
– наклонная асимптота графика.
Экстремумы функции:
Т. к. при , , а при , , то – точка минимума.
Т. к. при , , а при , , то – точка максимума.
На отрезках – функция убывает.
На отрезке – функция возрастает.
Точки перегиба графика функции
Точек перегиба нет.
При функция выпукла вниз.
При функция выпукла вверх.
На основании полученных данных построим график.
skachate.ru
Вычислить пределы используя правило лопиталя — Адвокатский клуб
Содержание страницы:
Правило Лопиталя
Введите функцию и точку для предела, которому надо применить правило Лопиталя
Вычислим предел функции с помощью правила Лопиталя. Вы введёте функцию, для которой требуется вычислить предел и точку в которой предел должен сходиться.
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
absolute(x) Абсолютное значение x
(модуль x или |x|) arccos(x) Функция — арккосинус от x arccosh(x) Арккосинус гиперболический от x arcsin(x) Арксинус от x arcsinh(x) Арксинус гиперболический от x arctg(x) Функция — арктангенс от x arctgh(x) Арктангенс гиперболический от x e e число, которое примерно равно 2.7 exp(x) Функция — экспонента от x (что и e^x) log(x) or ln(x) Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) pi Число — «Пи», которое примерно равно 3.14 sin(x) Функция — Синус от x cos(x) Функция — Косинус от x sinh(x) Функция — Синус гиперболический от x cosh(x) Функция — Косинус гиперболический от x sqrt(x) Функция — квадратный корень из x sqr(x) или x^2 Функция — Квадрат x tg(x) Функция — Тангенс от x tgh(x) Функция — Тангенс гиперболический от x cbrt(x) Функция — кубический корень из x floor(x) Функция — округление x в меньшую сторону (пример floor(4.5)==4.0) sign(x) Функция — Знак x erf(x) Функция ошибок (Лапласа или интеграл вероятности)
В выражениях можно применять следующие операции:
Действительные числа вводить в виде 7.5, не 7,5 2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание
Нахождение предела функции в точке по правилу Лопиталя
Нахождение предела функции, по правилу Лопиталя, раскрывающий неопределённости вида 0/0 и ∞/∞.
Калькулятор ниже находит предел функции по правилу Лопиталя (через производные числителя и знаменателя). Описание правила смотри ниже.
Предел функции в точке — правило Лопиталя
Допустимые операции: + — / * ^ Константы: pi Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch
Точка в которой необходимо посчитать предел
Правило Лопиталя
Если выполняются следующие условия:
- пределы функций f(x) и g(x) равны между собой и равны нулю или бесконечности:
или ; - функции g(x) и f(x) дифференцируемы в проколотой окрестности a;
- производная функции g(x) не равна нулю в проколотой окрестности a
- и существует предел отношения производной f(x) к производной g(x):
Тогда существует предел отношения функций f(x) и g(x):
,
И он равен пределу отношения производной функции f(x) к производной функции g(x):
В формуле допускается использование числа пи (pi), экспоненты (e), следующих математических операторов:
+ — сложение
— — вычитание
* — умножение
/ — деление
^ — возведение в степень
и следующих функций:
- sqrt — квадратный корень
- rootp — корень степени p, например root3(x) — кубический корень
- exp — e в указанной степени
- lb — логарифм по основанию 2
- lg — логарифм по основанию 10
- ln — натуральный логарифм (по основанию e)
- logp — логарифм по основанию p, например log7(x) — логарифм по основанию 7
- sin — синус
- cos — косинус
- tg — тангенс
- ctg — котангенс
- sec — секанс
- cosec — косеканс
- arcsin — арксинус
- arccos — арккосинус
- arctg — арктангенс
- arcctg — арккотангенс
- arcsec — арксеканс
- arccosec — арккосеканс
- versin — версинус
- vercos — коверсинус
- haversin — гаверсинус
- exsec — экссеканс
- excsc — экскосеканс
- sh — гиперболический синус
- ch — гиперболический косинус
- th — гиперболический тангенс
- cth — гиперболический котангенс
- sech — гиперболический секанс
- csch — гиперболический косеканс
- abs — абсолютное значение (модуль)
- sgn — сигнум (знак)
пределы — Вычислить предел используя правило Лопиталя:
Вычислить предел используя правило Лопиталя:
задан 20 Дек ’15 16:42
Найдём логарифм предела. Получится $%\dfrac+3x)>$%. Пусть $%x\to+\infty$%. Получается неопределённость типа $%\frac$%. Без учёта множителя $%\frac23$%, продифференцируем числитель и знаменатель. Производная числителя равна $%\dfrac+3>+3x>$%, и её предел равен нулю. Производная знаменателя равна 1. Значит, логарифм предела равен нулю, и сам предел равен 1 при $%x\to+\infty$%.
Теперь пусть $%x\to-\infty$%. Снова имеем неопределённость прежнего типа, и применяем правило Лопиталя. Производная числителя тождественно равна $%\dfrac>$%, и её предел равен $%-1$%, так как $%x3^$% здесь стремится к нулю, поскольку экспонента растёт быстрее линейной функции. Производная знаменателя та же самая. Таким образом, логарифм предела оказывается равен $%-\frac23$%, а сам предел равен $%e^$% при $%x\to-\infty$%.
Ввиду того, что два найденных односторонних предела не равны, можно сделать вывод, что предела функции при $%x\to\infty$% не существует.
отвечен 20 Дек ’15 19:07
@falcao. А разве мы не можем в ответе дать оба значения пределов: на +oo и -оо?
@nynko: можем. Но я именно эту информацию по отдельности и дал. Остальное зависит от того, что понимали авторы условия. Если исходить из определения, то предела не существует, хотя односторонние пределы имеются.
Здравствуйте
Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
задан
20 Дек ’15 16:42
показан
374 раза
обновлен
20 Дек ’15 22:38
Правило Лопиталя: теория и примеры решений
Правило Лопиталя и раскрытие неопределённостей
Раскрытие неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций значительно упрощается с помощью правила Лопиталя (на самом деле двух правил и замечаний к ним).
Суть правил Лопиталя состоит в том, что в случае, когда вычисление предела отношений двух бесконечно малых или бесконечно больших функций даёт неопределённости видов 0/0 или ∞/∞, предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.
Перейдём к формулировкам правил Лопиталя.
Правило Лопиталя для случая предела двух бесконечно малых величин. Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, может быть, самой точки a, причём в этой окрестности g‘(x)≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны нулю
(),
то предел отношения этих функций равен пределу отношения их производных
().
Правило Лопиталя для случая предела двух бесконечно больших величин. Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, может быть, самой точки a, причём в этой окрестности g‘(x)≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности
(),
то предел отношения этих функций равен пределу отношения их производных
().
Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный или бесконечный).
Замечания.
1. Правила Лопиталя применимы и тогда, когда функции f(x) и g(x) не определены при x = a.
2. Если при вычисления предела отношения производных функций f(x) и g(x) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).
3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a, а к бесконечности (x → ∞).
К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.
Раскрытие неопределённостей видов «ноль делить на ноль» и «бесконечность делить на бесконечность»
Пример 1. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x=2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем
В числителе вычисляли производную многочлена, а в знаменателе — производную сложной логарифмической функции. Перед последним знаком равенства вычисляли обычный предел, подставляя вместо икса двойку.
Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Решение. Подстановка в заданную функцию значения x=0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:
Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Решение. Подстановка в заданную функцию значения x=0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:
Пример 4. Вычислить
.
Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:
Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.
Пример 5. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
.
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида ∞/∞.
Пример 6. Вычислить
.
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида 0/0.
Пример 7. Вычислить
.
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида — ∞/∞, а затем неопределённость вида 0/0.
Пример 8. Вычислить
.
Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида ∞/∞, а затем неопределённость вида 0/0.
Применить правило Лопиталя самостоятельно, а затем посмотреть решение
Пример 9. Вычислить
.
Подсказка. Здесь придётся попыхтеть несколько больше обычного над преобразованием выражений под знаком предела.
Пример 10. Вычислить
.
Подсказка. Здесь правило Лопиталя придётся применять трижды.
Раскрытие неопределённостей вида «ноль умножить на бесконечность»
Пример 11. Вычислить
.
(здесь неопределённость вида 0∙∞ мы преобразовали к виду ∞/∞, так как
а затем применили правила Лопиталя).
Пример 12. Вычислить
.
В этом примере использовано тригонометрическое тождество .
Раскрытие неопределённостей видов «ноль в степени ноль», «бесконечность в степени ноль» и «один в степени бесконечность»
Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида
Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .
Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:
Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.
Пример 13. Вычислить, пользуясь правилом Лопиталя
.
Вычисляем предел выражения в показателе степени
.
.
Пример 14. Вычислить, пользуясь правилом Лопиталя
.
Вычисляем предел выражения в показателе степени
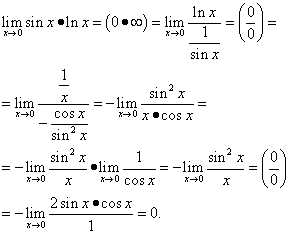 .
.
.
Пример 15. Вычислить, пользуясь правилом Лопиталя
.
Вычисляем предел выражения в показателе степени
.
Раскрытие неопределённостей вида «бесконечность минус бесконечность»
Это случаи, когда вычисление предела разности функций приводит к неопределённости «бесконечность минус бесконечность»: .
Вычисление такого предела по правилу Лопиталя в общем виде выглядит следующим образом:
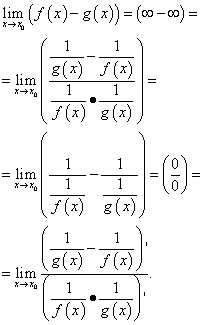
В результате таких преобразований часто получаются сложные выражения, поэтому целесообразно использовать такие преобразования разности функций, как приведение к общему знаменателю, умножение и деление на одно и то же число, использование тригонометрических тождеств и т.д.
Пример 16. Вычислить, пользуясь правилом Лопиталя
.
Решение. Пользуясь вышеперечисленными рекомендациями, получаем
Пример 17. Вычислить, пользуясь правилом Лопиталя
.
Решение. Пользуясь вышеперечисленными рекомендациями, получаем
Правило Лопиталя с примерами
Правило Лопиталя (п. Л.) облегчает вычисление пределов функций. Например, надо найти предел функции, которая является отношением функций стремящихся к нулю. Т.е. отношение функций это неопределенность 0/0. Раскрыть ее поможет
1. Неопределенность 0/0. Первое п.Л.
Если = 0, то , если последний существует.
2. Неопределенность вида ∞/∞ Второе п. Л.
Нахождение пределов такого типа называется раскрытием неопределенностей.
Если = ∞, то , если последний существует.
3. Неопределенности 0⋅∞, ∞- ∞, 1 ∞ и 0 0 сводятся к неопределенностям 0/0 и ∞/∞ путем преобразований. Такая запись служит для краткого указания случая при отыскании предела. Каждая неопределенность раскрывается по своему. Правило Лопиталя можно применять несколько раз, пока не избавимся от неопределенности. Применение правила Лопиталя приносит пользу тогда, когда отношение производных удается преобразовать к более удобному виду легче, чем отношение функций.
- 0⋅∞ произведение двух функций, первая стремится к нулю, вторая к бесконечности;
- ∞- ∞ разность функций, стремящихся к бесконечности;
- 1 ∞ степень, ее основание стремится к единице, а показатель к бесконечности;
- ∞ 0 степень, ее основание стремится к бесконечности, а степень к нулю;
- 0 0 степень, ее основание стремится к 0 и показатель тоже стремятся к нулю.
Пример 1. В этом примере неопределенность 0/0
Пример 2. Здесь ∞/∞
В этих примерах производные числителя делим на производные знаменателя и подставляем предельное значение вместо х.
Пример 3. Вид неопределенности 0⋅∞ .
Неопределенность 0⋅∞ преобразуем к ∞/∞, для этого х переносим в знаменатель в виде дроби 1/x , в числителе пишем производную от числителя, а в знаменателе производную от знаменателя.
Пример 4 Вычислить предел функции
Здесь неопределенность вида ∞ 0 Сначала логарифмируем функцию, затем найдем от нее предел
Для получения ответа надо е возвести в степень -1, получим e -1 .
Пример 5. Вычислить предел от если x → 0
Решение. Вид неопределенности ∞ -∞ Приведя дробь к общему знаменателю перейдем от ∞-∞ к 0/0. Применим правило Лопиталя, однако снова получим неопределенность 0/0, поэтому п. Л. надо применить второй раз. Решение имеет вид:
= = = =
= =
Пример 6 Решить
Решение. Вид неопределенности ∞/∞, раскрыв ее получим
= = = 0.
В случаях 3), 4), 5) сначала логарифмируют функцию и находят предел логарифма, а затем искомый предел е возводим в полученную степень.
Пример 7. Вычислить предел
Решение. Здесь вид неопределенности 1 ∞ . Обозначим A =
Тогда lnA = = = = 2.
Основание логарифма е, поэтому для получения ответа надо е возвести в квадрат, получим e 2 .
Иногда бывают случаи, когда отношение функций имеет предел, в отличие от отношения производных, которое не имеет его.
Т.к. sinx ограничен, а х неограниченно растет, второй член равен 0.
Эта функция не имеет предела, т.к. она постоянно колеблется между 0 и 2, к этому примеру неприменимо п. Л.
Еще по теме:
- Пособие по уходу за ребенком до 3 лет янао Детские пособия в Ямало-Ненецком автономном округе и Салехарде в 2018 году 2013 год запомнился для жителей Ямало-Ненецкого автономного округа резким снижением количества населения. Основной причиной сокращения жителей стала миграционная убыль. Чтобы исправить данную ситуацию власти стали […]
- Правило нахождения части от части Урок по математике по теме “Нахождение части целого и целого по его части” Разделы: Математика Тема урока: «Нахождение части целого и целого по его части». Цель урока: Научиться находить дробь от числа и число по его дроби. Обобщить понятие обыкновенной дроби и действий с […]
- Правила фильтрации данных Правила фильтрации данных Фильтрация данных (отображение только тех данных, которые удовлетворяют некоторому условию) осуществляется по значениям, отображаемым в колонках, при помощи строки фильтра. Строка фильтра расположена ниже заголовка колонки. Фильтрация данных может осуществляться […]
- Пособия в республике татарстан Детские пособия в Казани и Республике Татарстан в 2018 году В Республике Татарстан значительных проблем с демографией в последние годы не наблюдалось. Здесь традиционно высокий уровень рождаемости. Это позволяет местным властям направить усилия на поддержание самых нуждающихся слоев […]
- Bnc выход разрешение МОНИТОР ДЛЯ СИСТЕМЫ ВИДЕОНАБЛЮДЕНИЯ Давайте посмотрим каким должен быть монитор для видеонаблюдения и как правильно его выбрать. Начнем с того чем отличается специализированный монитор для работы в составе системы видеомониторинга от компьютерного. Главное отличие — наличие BNC входа. […]
- Пособие за роды воронеж Детские пособия в Воронеже и Воронежской области в 2018 году Воронежский регион относится к числу депрессивных по демографическим показателям. Убыль населения стартовала в 1995 году и до сих пор продолжается. Этот фактор влияет на особенности социальной политики местных […]
- Сколько отсудить алименты С какого момента и до скольки лет платят алименты? Выплата алиментов после 18. Под алиментами Семейный кодекс РФ понимает возложенные на дееспособных членов семьи обязательства по содержанию детей и родителей. Данные отношения урегулированы нормами раздела V СК РФ, которые содержат […]
- Бланк декларация налога на прибыль 2018 Как с вами связаться? Онлайн-сервисподготовки налоговой декларации по прибыли за 2018 год Сервис позволяет: Подготовить отчет Сформировать файл Протестировать на ошибки Распечатать отчет Отправить через интернет! Скачать новую форму декларации по налогу на прибыль за 2018 […]
bouncekitchen.ru



