Задача коши для дифференциального уравнения первого порядка – Дифференциальные уравнения первого порядка, теорема Коши | Высшая математика | Студенту | Статьи и обсуждение вопросов образования в Казахстане | Образовательный сайт Казахстана
- Комментариев к записи Задача коши для дифференциального уравнения первого порядка – Дифференциальные уравнения первого порядка, теорема Коши | Высшая математика | Студенту | Статьи и обсуждение вопросов образования в Казахстане | Образовательный сайт Казахстана нет
- Советы абитуриенту
- 6.02. Задача Коши для дифференциального уравнения первого порядка
- 2. Начальные условия и задача коши
- 2.2.Задача Коши для уравнения первого порядка, не разрешенного относительно производной
- 1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
- Дифференциальные уравнения первого порядка. Задача Коши
- Конспект лекции_6 Дифференциальные уравнения первого порядка
- 59.Задача Коши, начальные условия. Теорема существования и единственности решения задачи Коши для уравнения . Особые точки. Особые решения. Примеры.
6.02. Задача Коши для дифференциального уравнения первого порядка
Общее решение любого дифференциального уравнения первого порядка F(х; у; у’) = 0, как это следует из схемы его получения (1.3), содержит бесчисленное множество частных решений. Возникает естественный вопрос: как из этого множество частных решений выделить интересующее нас конкретное частное решение? Иначе говоря, как из множества интегральных кривых данного дифференциального уравнения выделить нужную интегральную кривую?
Ответ почти очевиден: для этого на плоскости Хоу нужно задать некоторую точку , через которую должна пройти искомая интегральная кривая. Тогда её уравнение и будет тем частным решением, которое выделяется из прочих (рис. 6.2).
Задание точки равносильно заданию условия для искомого, выделяемого из прочих, частного решения данного дифференциального уравнения. Это условие называется Начальным условием для дифференциального уравнения первого порядка F(х; у; у’) = 0. Начальным оно называется потому, что очень часто в реальных задачах по исследованию различного рода процессов роль независимой переменной
Если дифференциальное уравнение первого порядка F(х; у; у’) = 0 задано вместе с начальным для него условием , То говорят, что для этого уравнения задана Задача Коши:
(2.1)
Решить её – это значит найти те частные решения дифференциального уравнения F(х; у; у’) = 0 , которые еще удовлетворяют и заданному начальному условию . С точки зрения рисунка 6.2 решить задачу Коши (2.1) – это значит найти уравнения всех интегральных кривых дифференциального уравнения F(х; у; у’) = 0, проходящих через начальную точку .
Как правило, задача Коши (2.1) имеет единственное решение . То есть через заданную начальную точку проходит единственная интегральная кривая дифференциального уравнения F(х; у; у’) = 0 (как на рис. 6.2). Но бывает, что задача Коши не имеет решений. То есть бывает, что ни одна из интегральных кривых не проходит через заданную начальную точку . Тогда такая точка называется Особой точкой дифференциального уравнения. А бывает, что задача Коши имеет несколько решений. То есть бывает, что через начальную точку проходит несколько интегральных кривых. Сколько решений будет у задачи Коши (2.1) и каковы они, выясняется в процессе её решения. А Схема решения задачи Коши (2.1) такова:
1. Решаем дифференциальное уравнение F(х; у; у’) = 0 и находим все его решения. То есть находим общее решение (общий интеграл) и возможные особые решения .
2. Подставляем начальные значения Х = х0 И У = у0 в общее решение и находим соответствующее значение (значения) константы С:
(2.2)
3. Подставляем каждое из найденных значений С В общее решение и получаем частные решения
,
Являющиеся решением задачи Коши. Это те решения этой задачи, которые выделяются из общего решения дифференцированного уравнения F(х; у; у’) = 0.
4. Проверяем, нет ли среди особых решений Дифференциального уравнения F(х; у; у’) = 0 таких, которые удовлетворяют начальному условию У(х0) = у0. Если такие найдутся, они тоже будут решениями задачи Коши (2.1).
Пример1. Решить задачу Коши:
Решение.
1. Сначала решим дифференциальное уравнение . Оно уже решено ранее – его решение найдено в примере 3, §1:
– общее решение; – особое решение.
2. Подставим начальные значения В общее решение и найдем С:
3. Подставим в общее решение и получим частное решение
.
Эта функция является решением данной задачи Коши.
4. Обратим внимание на особое решение У=0. Начальному условию У(0)=1 оно не удовлетворяет, поэтому решением данной задачи Коши не является.
Ответ: – единственное решение поставленной задачи Коши.
Пример 2. Материальное тело поднято на высоту H и в начальный момент времени T=0 отпущено в свободное падение. Описать математически процесс падения тела. А именно, найти зависимость ν = ν(T) скорости ν падающего тела от времени T, и найти зависимость S = S(T) пути S, пройденного падающим телом, от времени T. Сопротивлением воздуха пренебречь.
Решение. Как известно, все свободно падающие тела падают с постоянным ускорением G ≈ 9,8 м/сек2 – с ускорением свободного падения. А так как ускорение – это производная от скорости, то получаем: . Это – дифференциальное уравнение первого порядка для искомой функции
Решим эту задачу.
1. Сначала решим дифференциальное уравнения:
Это – общее решение уравнения , содержащее все его решения. Особых решений у него нет.
2. Используем начальное условие и найдем С:
0 = G0+С => С = 0.
3. Подставим С=0 в общее решение V=Gt+C и получим окончательно: V=Gt. Это и есть решение поставленной задачи Коши (единственное). И заодно V=Gt – это искомая зависимость скорости V падающего тела от времени T.
А теперь займёмся поиском зависимости S=S(t) Пути S От времени T. Учтём, что и что . Тогда для определения этой зависимости получим следующую задачу Коши:
Решим эту задачу.
1. Сначала решим дифференциальное уравнение :
;
Это – общее решение уравнения , содержащее все его решения. Особых решений у него нет.
2. Используем начальное условие и найдём С:
.
3. Подставим С=0 в общее решение и получим окончательно: . Это и есть решение рассматриваемой задачи Коши. И заодно – это искомая зависимость пути S, проходимого свободно падающим телом, от времени T.
Ответ: – известные школьные формулы.
Пример3. Дать математическое описание демографического процесса (процесса изменение численности населения со временем) для достаточно крупного населённого региона, если в начальный момент времени численность населения региона составляла человек.
;
Здесь и – некоторые числовые коэффициенты, связанные соответственно с уровнем рождаемости и уровнем смертности в данном регионе. Тогда общее изменение численности населения за время найдется по формуле:
.
Здесь . Из получённого равенства следует: . Устремляя здесь (при этом, очевидно, и ), то есть переходя к бесконечно малым и , получим:
, или .
Это – дифференциальное уравнение первого порядка для искомой функции . Дополняя это заданным начальным условием , получим для этой функции задачу Коши:
Решим эту задачу.
1. Сначала решим дифференциальное уравнение . Функция является его очевидным частным решением. Но это, очевидно, не та функция, которую мы ищем – она не удовлетворяет начальному условию, да и вообще она означает, что население в регионе отсутствует.
Будем искать те решения уравнения для которых :
Итак, – общее решение дифференциального уравнения . В него, кстати, при С = 0 входит и отмеченное ранее нулевое решение . То есть в найденном общем решении содержатся все решения дифференциального уравнения.
2. Используем начальное условие и найдём С:
.
3. Подставим в общее решение и получим искомое решение задачи Коши:
.
Это и есть искомая зависимость Численности населения региона от времени .
Проанализируем эту зависимость.
а) Если , то численность населения экспоненциально растёт со временем (рис. 6.3(а)).
б) Если , то численность населения Экспоненциально убывает со временем (рис. 6.3(б)).
в) Если , то , то есть численность населения региона не меняется (рис. 6.3(в).
Какой именно будет величина для данного региона, можно выяснить опытным путём. Пусть, например, перепись населения показала, что в некоторый момент времени в регионе проживало человек. Подставляя эти данные в формулу , можем найти :
.
Примечание. Полученная формула будет верно описывать демографический процесс в регионе, если уровень рождаемости и уровень смертности в нем не меняются со временем. То есть если коэффициенты и рождаемости и смертности не меняются со временем. А значит, если не меняется со временем и итоговый коэффициент . Но это, как известно, не так: с течением времени, в силу разных причин, ситуация и со смертностью, и с рождаемостью может существенно измениться. Поэтому полученную формулу при конкретном числовом значении оправданно применять лишь на протяжении достаточно ограниченного периода времени. В другой период времени тоже можно применять эту формулу, но уже при другом значении .
Пример 4. Рассмотрим задачу о математической модели естественного роста выпуска продукции.
Пусть – объем продукции некоторого предприятия, реализованной моменту времени . Будем считать, что вся продукция реализуется по некоторой фиксированной цене за единицу продукции независимо от объема продаж . Это значит, что рынок данной продукции длительное время является насыщенным – удается продавать по фиксированной цене практически любые объемы этой продукции.
Доход от продаж составит: . Будем считать, что некоторая часть этого дохода используется в качестве инвестиций в производство выпускаемой продукции. То есть объем инвестиций составит:
(2.4)
Здесь – так называется Норма инвестиций. Она показывает, какая часть дохода возвращается в производство.
Чем больше объем инвестиций , тем быстрее растёт объем производства . В модели естественного роста это значит, что скорость роста объема производства (так называемая
. (2.5)
Здесь
(2.6)
– так называемая Норма акселерации, которая показывает, каким должен быть объём инвестиций , чтобы обеспечить единичную скорость роста объема производства (обеспечить рост на единицу продукции за единицу времени). Подставляя (2.4) в (2.5), получим
, (2.7)
Где – числовой коэффициент. Равенство (2.7) представляет собой дифференциальное уравнение первого порядка для функции . Дополняя его некоторым начальным условием , получим задачу Коши:
(2.8)
Эта задача полностью совпадает с задачей Коши для демографического процесса (см. пример 3). Значит, у них полностью совпадают и решения:
(2.9)
Заметим, что условие постоянства цены единицы продаваемой продукции, то есть условие насыщенности рынка, не может выполнятся всегда, при любых . С увеличением объема продаж на некотором этапе рынок насыщается, спрос на товар падает, и дальнейшее увеличении объема продаж возможно лишь при снижении цены на него – в соответствии с классической убывающей кривой спроса . Если учесть эту зависимость от , то выражение (2.4) для примет вид:
(2.10)
А вместо (2.7) из (2.5) получим:
, (2.11)
Где . Это дифференциальное уравнение вместе с начальным условием составит задачу Коши:
(2.12)
Для определения функции , характеризующей объем продаж при насыщенном спросе, когда рост объема продаж возможен лишь при снижении цены на продаваемую продукцию. Эта функция, естественно, будет отличаться от функции (2.9) (будет более сложной).
Упражнения
1. Сформулировать и решить задачу по определению скорости V=V(T) свободно падающего тела массой M при условии, что учитывается сопротивление воздуха, пропорциональное скорости падения тела.
Ответ: .
2. Сформулировать и решить задачу по определению объема У=y(t) реализованной продукции, если известно, что кривая спроса Р= р(у) задаётся уравнением Р=2-у; норма инвестиций M=0,5; норма акселерации ; У(0)=0,5 – начальное условие.
Ответ:
3. При условиях предыдущей задачи 2 найти эластичность объема продаж относительно цены Р и определить условия, при которых продажи продукции являются эластичными и неэластичными.
Ответ: .
Если 0,5<Y<1, то есть если , то , и продажи представляют собой эластичный процесс (продажи растут относительно быстрее снижения цены). Доход от продаж при снижении цены возрастает. А если 1<Y<2, то есть если , то , и продажи представляют собой неэластичный процесс (продажи растут относительно медленнее снижения цены). Доход от продаж растёт при увеличении цены товара (см. §7 главы 4).
| < Предыдущая | Следующая > |
|---|
matica.org.ua
2. Начальные условия и задача коши
Определение. Начальные
условия для дифференциального уравнения  -го
порядка — это набор чисел
-го
порядка — это набор чисел
, (2)
задающий
для фиксированного значения независимой
переменной  значения неизвестной функциии ее производных вплоть до порядка, на
единицу меньшего порядка уравнения:
значения неизвестной функциии ее производных вплоть до порядка, на
единицу меньшего порядка уравнения:
.
Определение. Задачей
Коши для дифференциального уравнения
называется задача отыскания решения 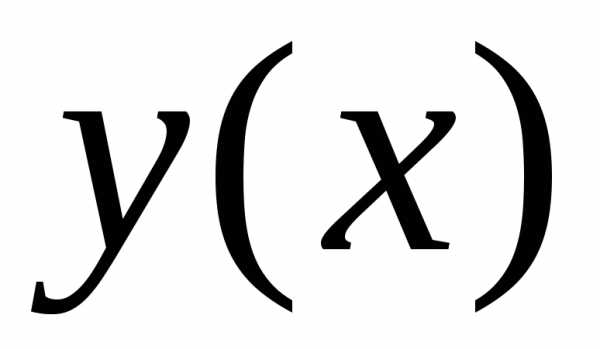 ,
отвечающего заданным начальным условиям.
,
отвечающего заданным начальным условиям.
Геометрический смысл задачи Коши для дифференциального уравнения 1-го порядка
Для
дифференциального уравнения 1-го порядка
(при 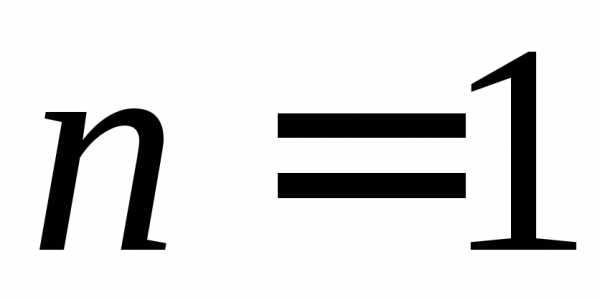 )
начальные условия (2) имеют вид пары
чисел
)
начальные условия (2) имеют вид пары
чисел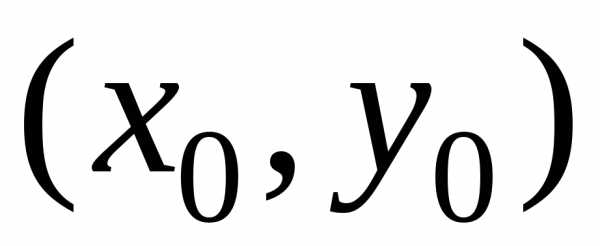 .
Тем самым ставится задача отыскания
решения
.
Тем самым ставится задача отыскания
решения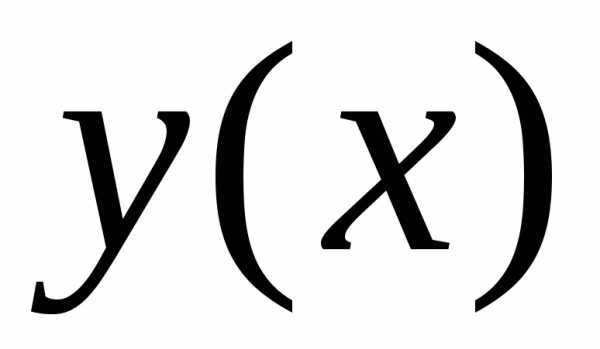 ,
для которого.
Геометрически это означает выбор из
совокупности интегральных кривых той,
которая проходит через заданную точку
плоскости
,
для которого.
Геометрически это означает выбор из
совокупности интегральных кривых той,
которая проходит через заданную точку
плоскости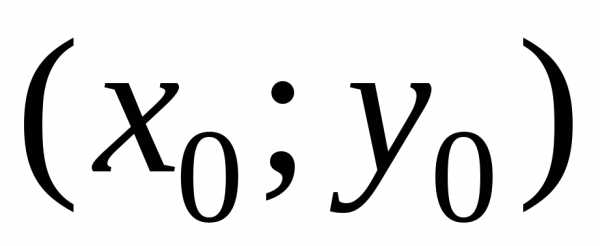 (рис. 1).
(рис. 1).
Рис. 1
Геометрический смысл задачи Коши для дифференциального уравнения 2-го порядка
Для
дифференциального уравнения 2-го порядка
(при  )
начальные условия (2) имеют вид тройки
чисел,
и ставится задача отыскания решения
)
начальные условия (2) имеют вид тройки
чисел,
и ставится задача отыскания решения ,
для которогои.
Геометрически это означает выбор из
совокупности интегральных кривых той,
которая, во-первых, проходит через
заданную точку плоскости
,
для которогои.
Геометрически это означает выбор из
совокупности интегральных кривых той,
которая, во-первых, проходит через
заданную точку плоскости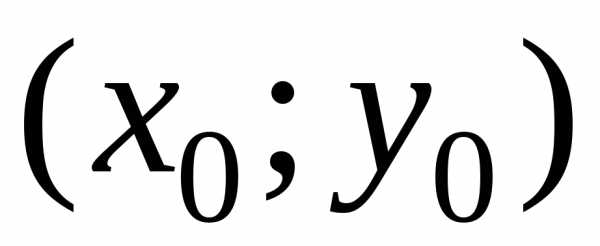 ,
и, во-вторых, имеет в этой точке заданный
угловой коэффициент касательной
,
и, во-вторых, имеет в этой точке заданный
угловой коэффициент касательной (рис. 2).
(рис. 2).
М0
Рис. 2
3. Общее решение и общий интеграл
Начальные
условия
,
будучи набором из  чисел, задают точку пространства
чисел, задают точку пространства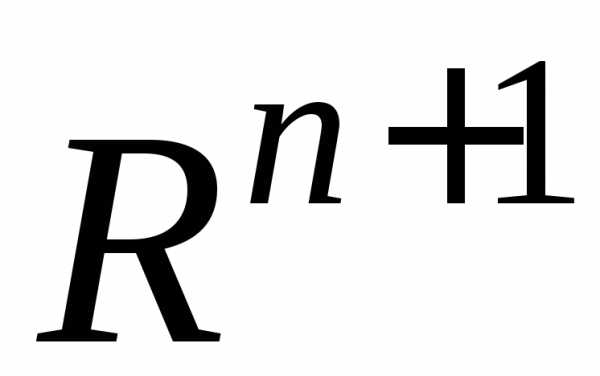 .
Множество всех рассматриваемых вариантов
начальных условий образует некоторую
область.
.
Множество всех рассматриваемых вариантов
начальных условий образует некоторую
область.
Для
различных видов ограничений на функцию  и на область
и на область имеет место существование и единственность
решения задачи Коши для начальных
условий из
имеет место существование и единственность
решения задачи Коши для начальных
условий из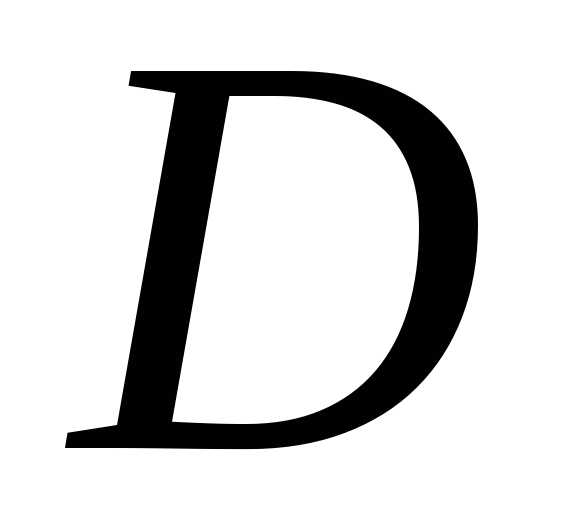 .
Приведем примеры соответствующих
теорем.
.
Приведем примеры соответствующих
теорем.
I.
Пусть уравнение 1-го порядка является
разрешённым относительно производной 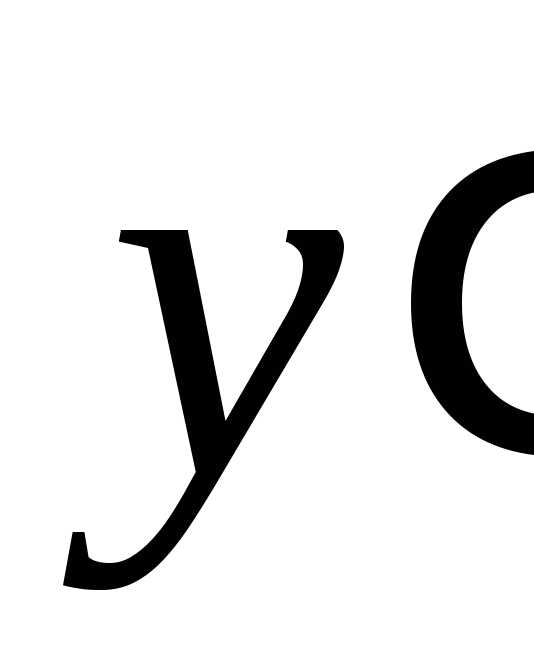 :
:
.
Теорема 1. Если
функция 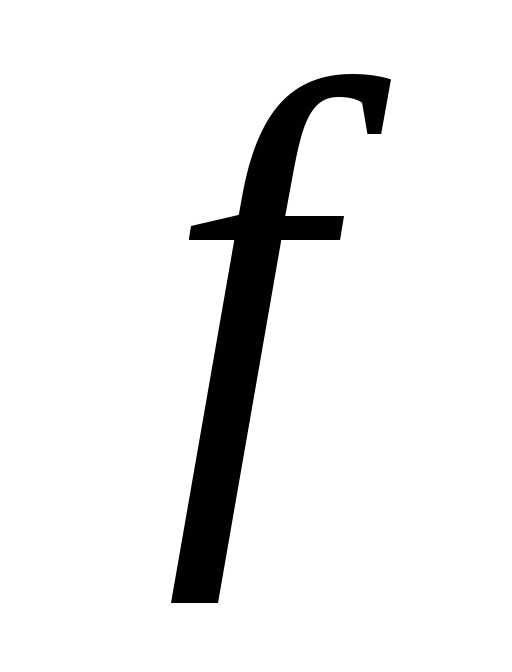 и ее частная производная
и ее частная производная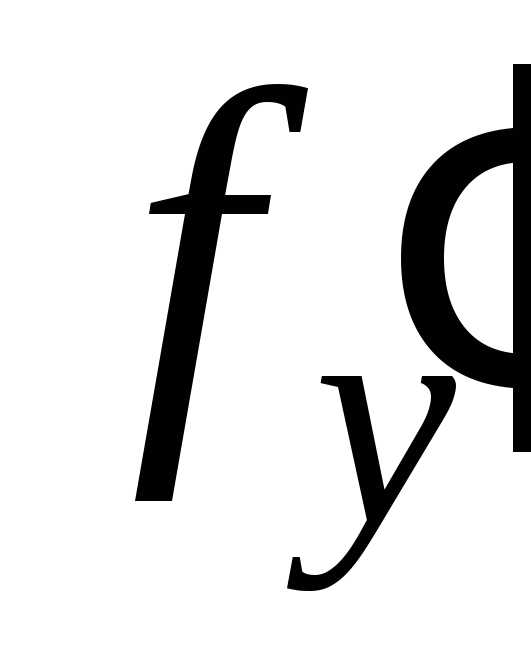 непрерывны в области
непрерывны в области плоскости
плоскости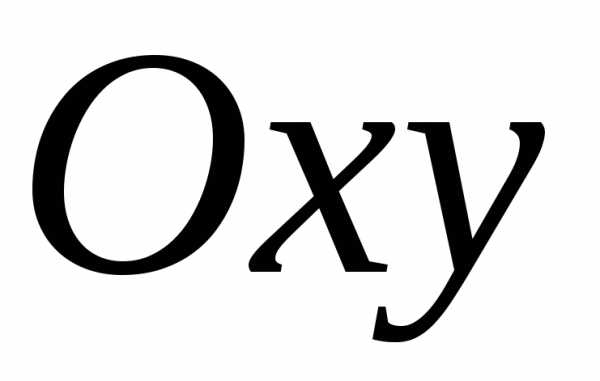 ,
то решение задачи Коши для любых начальных
условийсуществует и единственно в некоторой
окрестности точки
,
то решение задачи Коши для любых начальных
условийсуществует и единственно в некоторой
окрестности точки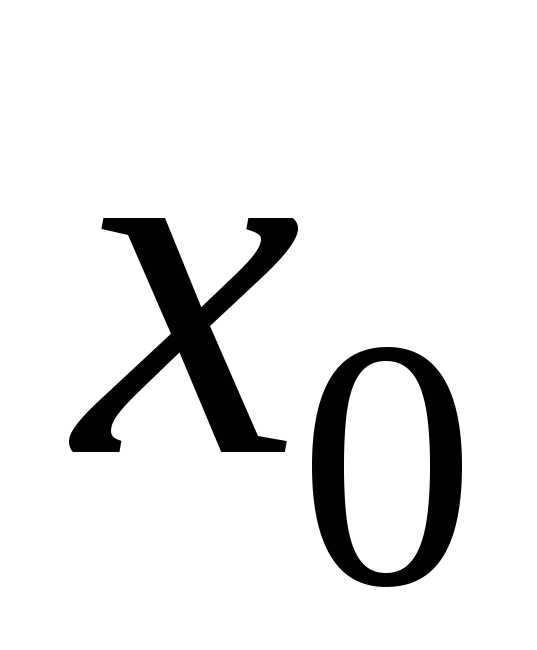 .
.
II. Пусть
уравнение 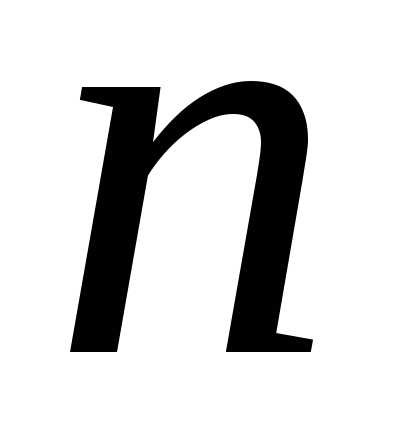 -го
порядка является разрешённым относительно
старшей производной
-го
порядка является разрешённым относительно
старшей производной 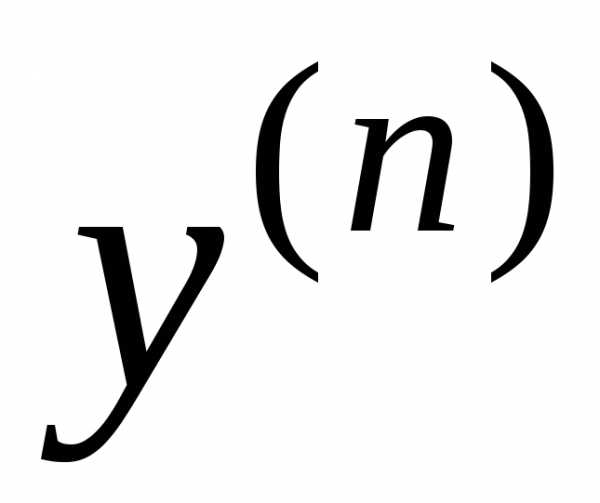 :
:
.
Теорема 2. Если
функция  и ее частные производныенепрерывны в области
и ее частные производныенепрерывны в области -мерного
пространства,
то решение задачи Коши для любых начальных
условийсуществует и единственно в некоторой
окрестности точки.
-мерного
пространства,
то решение задачи Коши для любых начальных
условийсуществует и единственно в некоторой
окрестности точки.
В дальнейшем будем
предполагать, что дифференциальные
уравнения рассматриваются в области  существования и единственности решения.
существования и единственности решения.
Определение. Общим решением дифференциального уравнения  -го
порядка называется функция
,
зависящая от аргумента
-го
порядка называется функция
,
зависящая от аргумента и от
и от произвольных постоянных
произвольных постоянных ,
которая удовлетворяет двум условиям:
,
которая удовлетворяет двум условиям:
1) при любых значениях произвольных постоянных эта функция является решением;
2) за счет выбора значений произвольных постоянных можно получить решение задачи Коши для любых начальных условий из области существования и единственности решения.
Заметим, что количество произвольных постоянных равно порядку уравнения.
Определение. Частным решением дифференциального уравнения называется функция, которая получается из общего решения, если произвольным постоянным придать определенные значения.
Напомним определение
неявной функции: функция
в окрестноститочки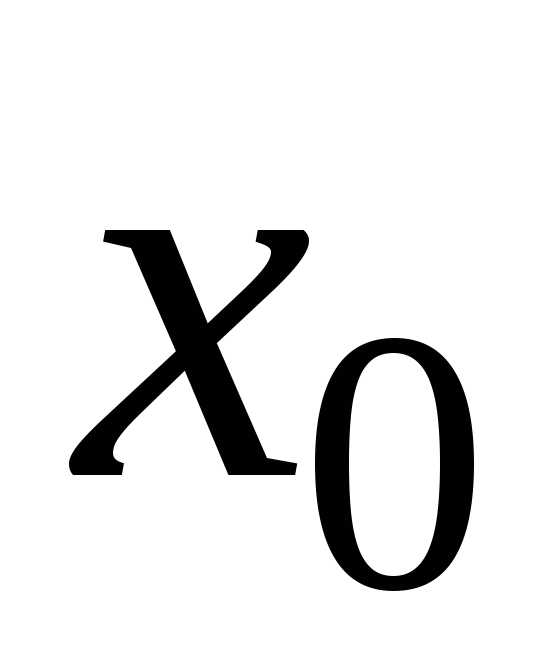 ,задана неявно уравнением ,
если при всех
,задана неявно уравнением ,
если при всех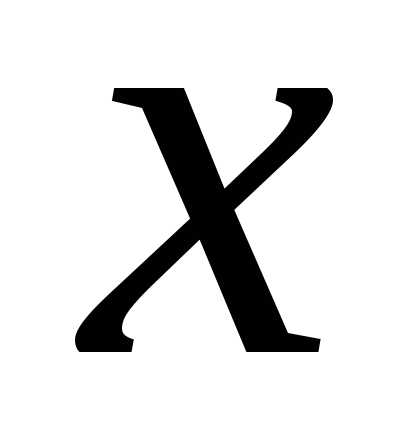 из этой окрестности справедливо равенство.
из этой окрестности справедливо равенство.
Обычное, «явное» задание функции можно рассматривать как частный случай неявного: ; здесь.
Определение. Общим
интегралом дифференциального уравнения  -го
порядка называется уравнение
-го
порядка называется уравнение
, (3)
зависящее от  произвольных постоянных
произвольных постоянных ,
которое задает общее решениекак неявную функцию.
,
которое задает общее решениекак неявную функцию.
Определение. Частным интегралом называется уравнение, которое получается из общего интеграла (3), если произвольным постоянным придать определенные значения.
Замечание. В тех случаях, когда удается найти
решение дифференциального уравнения,
оно имеет, как правило, вид общего
интеграла (3). Если при этом можно  явно выразить через(«разрешить уравнение относительно
явно выразить через(«разрешить уравнение относительно »),
то приходим к общему решению.
»),
то приходим к общему решению.
studfiles.net
2.2.Задача Коши для уравнения первого порядка, не разрешенного относительно производной
36 | Глава 2. Задача Коши |
ствование решения только на отрезке [t0 − h, t0 + h], где h = min{T,MA }
(см. рис. 2.1). Это объясняется тем, что мы должны следить за тем, чтобы точка (t, y(t)) не выходила за пределы прямоугольника Π, то есть чтобы выполнялось неравенство |y(t) − y0| 6 A, t [t0 − h, t0 + h]. Это необходимо, поскольку только в Π функция f(t, y) ограничена фиксированной постоянной M и удовлетворяет условию Липшица с фикси-
рованной константой L. Попытки увеличить число h = min{T, MA } за
счет увеличения A, вообще говоря, безрезультатны, поскольку при увеличении A в общем случае увеличивается постоянная M.
Приведем пример, показывающий, что без дополнительных предположений относительно функции f(t, y) решение существует только на достаточно малом отрезке.
Пример 2.1.1. Рассмотрим при a > 0 задачу Коши
y0(t) = a(y(t)2 + 1), y(0) = 0.
Функция f(t, y) = a(y2 + 1) определена при любых действительных t и y. Однако решение этой задачи y(t) = tg(at) существует только на
отрезке [−h2, h2], содержащемся в интервале −2πa,2πa .
2.2.1. Примеры постановки задачи Коши
Рассмотрим обыкновенное дифференциальное уравнение первого порядка, не разрешенное относительно производной
F (t, y(t), y0(t)) = 0. | (2.14) |
Всюду в этом параграфе будем считать, что функция F (t, y, p) определена в параллелепипеде D с центром в некоторой точке (t0, y0, y00 ) R3:
D = {(t, y, p) : |t − t0| 6 a, |y − y0| 6 b, |p − y00 | 6 c}, | (2.15) |
где a, b, c – фиксированные положительные числа.
Определение 2.2.1. Функция y(t) называется решением уравнения (2.14) на отрезке [t1, t2], если:

2.2.Задача Коши для уравнения, не разрешенного относительно y0 37
1.y(t) непрерывно дифференцируема на [t1, t2];
2.(t, y(t), y0(t)) D для всех t [t1, t2];
3.на отрезке [t1, t2] выполнено(2.14).
Если уравнение (2.14) разрешено относительно производной,
F (t, y, p) = p − f(t, y),
то при некоторых дополнительных условиях на функцию f(t, y) для получения единственного решения уравнения достаточно задать условие прохождения соответствующей интегральной кривой (графика решения) через некоторую точку (t0, y0). В общем случае приходим к задаче с дополнительным условием
F (t, y(t), y0(t)) = 0, y(t0) = y0. | (2.16) |
Проиллюстрируем особенности такой задачи для случая уравнения, квадратично зависящего от производной:
(y0(t))2 | − | (t + y(t))y0(t) + ty(t) = 0. | (2.17) |
|
|
Поскольку квадратное уравнение p2 − (t + y)p + ty = 0 имеет корни p1 = t, p2 = y, то исходное дифференциальное уравнение распадается на совокупность двух уравнений, разрешенных относительно производной:
|
| y0(t) = t, y0(t) = y(t). |
Получаем два семейства решений | ||
| t2 | |
y1(t) = |
| + C1, y2(t) = C2 exp{t}, C1, C2 R. |
2 | ||
Пример 2.2.1. Задача для уравнения (2.17) с дополнительным усло-
вием y(0) = 1 имеет два решения (см. рис. 2.2а): |
| |
| t2 |
|
y1(t) = | 2 + 1, y2(t) = exp{t}. | (2.18) |
Задача для уравнения (2.17) c дополнительным условием y(0) = 0 имеет четыре решения (см. рис.2.2б-г):
|
| y1(t) = | t2 | y2(t) = 0, |
|
|
| ||
|
|
| , |
|
|
| |||
|
| 2 |
|
|
| ||||
3 | y2 | e | e | y1 | (t), t > 0. |
| |||
| (t), t > 0, |
|
| ||||||
y (t) = | y1 | (t), t < 0, | y4 | (t) = | y2 | (t), t < 0, | (2.19) | ||
e | e |
|
|
| e |
| e |
|
|
e |
|
|
|
| e |
|
| ||
38 | Глава 2. Задача Коши |
Рис. 2.2. К примерам 2.2.1, 2.2.2: неединственность решения задачи Коши.
Рассмотренный пример показывает, что неединственность решения достаточно характерна для задачи (2.16). Для единственности необходимо задать еще одно дополнительное условие. Из геометрических соображений наиболее естественно потребовать, чтобы искомое решение проходило через заданную точку с данным наклоном касательной. В результате приходим к постановке задачи Коши
F (t, y(t), y0(t)) = 0, y(t0) = y0, y0(t0) = y00 . | (2.20) |
Пример 2.2.2. Задача Коши для уравнения (2.17) с начальными условиями y(0) = 1, y0(0) = 0, то есть
(t | , y | , y0 | ) = (0, 1, 0), F (0, 1, 0) = 0, | ∂F (0, 1, 0) | = 1 = 0, | (2.21) | ||
∂p |
| |||||||
0 | 0 | 0 |
| − 6 | ||||
имеет единственное решение y(t) = t2 + 1.
2
Задача Коши для уравнения (2.17) с начальными условиями y(0) = 1, y0(0) = 1, то есть
|
|
| (t | , y | , y0 | ) = (0, 1, 1), | F (0, 1, 1) = 0, | ∂F (0, 1, 1) | = 1 = 0, | (2.22) | |||||||
|
|
|
| ||||||||||||||
|
|
| 0 | 0 | 0 |
|
|
|
|
|
|
| ∂p |
| 6 | ||
имеет единственное решение y(t) = exp{t}. |
|
|
|
| |||||||||||||
|
| Задача Коши для уравнения (2.17) с начальными условиями y(0) = | |||||||||||||||
1 | , | y0 | (0) = y0 | y0 | 0; 1 | }, то есть |
|
|
|
|
|
|
| ||||
|
|
|
| 0, | 0 6 { |
|
|
|
|
|
|
| |||||
|
|
|
|
|
| (t | , y | , y0 | ) = (0, 1, y0 ), | F (t | , y | , y0 | ) = 0, | (2.23) | |||
|
|
|
|
|
| 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 6 |
| ||

2.2. Задача Коши для уравнения, не разрешенного относительно y0 39
не имеет ни одного решения.
Задача Коши для уравнения (2.17) с начальными условиями y(0) = 0, y0(0) = 0, то есть
(t | , y | , y0 | ) = (0, 0, 0), F (0, 0, 0) = 0, | ∂F (0, 0, 0) | = 0, | (2.24) |
| ||||||
0 | 0 | 0 |
| ∂p |
|
|
|
|
|
|
|
|
имеет четыре решения (2.19).
Приведенный пример показывает следующие особенности постановки задачи Коши (2.20):
1.тройка чисел (t0, y0, y00 ) R3 не может быть взята произвольно; для существования решения необходимо выполнения условия
F (t0, y0, y00 ) = 0;
2.двух дополнительных условий y(t0) = y0, y0(t0) = y00 может оказаться недостаточно для единственности решения в случае
∂F (t0, y0, y00 )= 0. ∂p
2.2.2.Теорема существования и единственности решения задачи Коши
Теорема 2.2.1. Пусть функция F (t, y, p) определена в параллелепипеде D, заданным (2.15), и выполнены следующие условия:
1. | F (t0, y0, y00 ) = 0; |
|
|
| (2.25) | ||||
2. | F (t, y, p), | ∂F (t, y, p) | , | ∂F (t, y, p) | непрерывны в D; (2.26) | ||||
|
| ∂y | ∂p |
| |||||
|
|
|
|
|
|
| |||
3. | ∂F (t0, y0, y00 ) | 6= 0. |
|
|
| (2.27) | |||
| ∂p |
|
|
|
|
| |||
Тогда найдется h > 0 такое, что на отрезке [t0 − h, t0 + h] существует единственное решение задачи Коши(2.20).
Доказательство. Рассмотрим в окрестности точки (t0, y0, y00 ) уравнение
Из условий (2.25)-(2.27) и теоремы о неявной функции следует, что найдется окрестность Ω0 точки (t0, y0), в которой существует единственная
40 | Глава 2. Задача Коши |
непрерывная функция p = f(t, y), имеющая в Ω0 непрерывную частную производную
∂f(t, y) | = − | ∂F (t, y, f(t, y))/∂y | , | (2.29) |
∂y | ∂F (t, y, f(t, y))/∂p |
и являющаяся решением уравнения (2.28). В частности, выполнено равенство
В окрестности Ω0 уравнение(2.14) эквивалентно дифференциальному уравнению y0(t) = f(t, y(t)), разрешенному относительно производной, а задача Коши(2.20) принимает вид
y0(t) = f(t, y(t)), y(t0) = y0. | (2.31) |
Отметим, что фигурирующее в (2.20) начальное условие на производную y0(t0) = y00 автоматически выполнено в силу равенства(2.30).
Рассмотрим задачу Коши (2.31) в прямоугольнике
Π = {(t, y) : |t − t0| 6 a0, |y − y0| 6 b0},
где положительные числа a0, b0 настолько малы, чтобы Π Ω0. Как уже установлено выше, функция f(t, y) непрерывна в Ω0, а значит и в Π. Условие Липшица для этой функции по переменной y на множестве Π с константой
(t,y) Π | ∂y |
|
|
| ||
L = max |
| ∂f (t, y) |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| ∂f |
|
вытекает из непрерывности в Π частной производной |
| (t, y), опреде- | ||||
∂y | ||||||
ленной в (2.29). Таким образом, в Π выполнены все условия теоремы2.1.2 существования и единственности решения задачи Коши для дифференциального уравнения, разрешенного относительно производной. Следовательно, найдется h > 0 такое, что на отрезке [t0 − h, t0 + h] существует единственное решение задачи Коши(2.31), а значит и задачи Коши(2.20).
Замечание 2.2.1. В приведенном выше примере 2.2.2 условия теоремы2.2.1 выполнены для задач Коши(2.21), (2.22) и не выполнены для задач Коши(2.23), (2.24).
studfiles.net
1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
Уравнения, связывающие независимую переменную, неизвестную функцию и её производные называют дифференциальным. Если искомая функция зависит от одной переменной, то Д.У. называют обыкновенным.
Если искомая функция зависит от нескольких переменных, то Д.У. называют уравнение частных производных.
Наивысший порядок производной, входящий в Д.У. называют порядком этого уравнения. Д.У. первого порядка называют выражение вида F(x,y,)=0(1). Если это уравнение удаётся разрешить относительно производной, то записывают = f(x,y)(2). Решением уравнения (1) и (2) называют такую дифференцируемую функцию y=которая при подстановке её в уравнение обращает его в верное тождество.
Задачей Коши либо начальной задачей называют задачу нахождения решения y=уравнения(2), удовлетворяющего начальному условию y(xo)=yo (3).
Общим решением Д.У. (2) называется функция y=(4), зависящая от переменной x и произвольной постоянной c. Общее решение (4) удовлетворяет условию уравнения (2) при любых значениях константы с.
Каково бы ни было начальное условие (3) можно подобрать значение со константы с, так чтобы функция y=удовлетворяла заданному начальному условию(3)(если выполнены условия теоремы Коши).
Частным решением Д.У. называют решение, полученное из общего решения (4) либо вида (4) при каком либо определённом значении постоянной произвольной с.
2. Теорема существования и единственности решения задачи Коши для дифференциального уравнения (д.У.) первого порядка.
Теорема Коши (существования и единственности): если функция f(x,y) непрерывна и имеет непрерывную производную в областиD, то решение Д.У. = f(x,y) с начальным условием y(xo)=yo , где точка с координатами (xo,yo) принадлежит D, существует и единственно, то есть через точку (xo,yo) принадлежащую области D проходит единственная интегральная кривая данного уравнения.
Если во всех точках решения y = Ψ(x) уравнения = f(x,y) условие действительности не выполняется, то такое решение называется особым. При этом через каждую точку Мо(xo,yo) особого решения проходит также и другое решение уравнения= f(x,y), которое не совпадает с решением y =Ψ(x) в сколь угодно малой окрестности этой точки.
3.ДУ 1-го порядка,интегрируемые в квадратурах.
1.Ур-ия с разделяющимися переменними
P(xy)dx+Q(xy)dy=0 (1). Ур-е(1) наз. ур-ем,записанным в диф-лах.,где x-аргумент,y-искомая ф-я, dx,dy-диф-лы, P(xy), Q(xy)-заданные непрерывные в некот.области D ф-ии.
Пусть P(xy)=p(x),а Q(xy)=q(y),тогда (1) примет вид (2): p(x)dx+q(y)dy=0. (2)наз.ДУ с разделёнными переменнымы, интегрируя которое мы получим:+=C-общий ин-л у-я(2). Если хотя бы один из интегралов неберущ.,то ДУ(2) всё равно считается решённым, при этом говорят, что решение найдено в квадратурах.Пусть P(xy)=(x)*(y), Q(xy)=(x)*(y), тогда (1) примет вид(3):(x)*(y)dx+(x)*(y)dy=0.У-е (3)-ДУ с разделяющимися переменными.Разделив (3) на (x)*(y) получаем:dx+dy=0,которое является ур-ем с разделёнными переменными: dx+=C. При таком решении могут быть потеряны корни (x)=0 и (y)=0,которые необходимо рассматривать отдельно.
studfiles.net
Дифференциальные уравнения первого порядка. Задача Коши
Определение 1Уравнение
| , | (1) |
связывающее независимую переменную х, неизвестную функцию и ее производные (наличие хотя бы одной производной обязательно), называется дифференциальным уравнением.
Если уравнение (1) можно записать в виде
| , | (2) |
где f – известная функция, то будем говорить, что дифференциальное уравнение разрешено относительно старшей производной . Оно называется дифференциальным уравнением в нормальной форме.
Определение 2Дифференциальное уравнение, в котором неизвестная функция у зависит от одной переменной х, называется обыкновенным (ОДУ). Если же дифференциальное уравнение содержит неизвестную функцию нескольких переменных и ее частные производные, то оно называется уравнением в частных производных.
Определение 3 Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.
Определение 4 Решением (интегралом) дифференциального уравнения n-го порядка называется любая функция, которая задана на промежутке, имеет на этом промежутке производную порядка n и обращает уравнение в верное равенство в каждой точке данного промежутка.
Определение 5 График решения дифференциального уравнения называется интегральной кривой.
Процесс нахождения решения дифференциального уравнения называется интегрированием этого уравнения. Решение может быть задано в неявном виде . В этом случае его называют интегралом дифференциального уравнения.
Определение 6 Общим решением дифференциального уравнения (1) называется функция
| , | (3) |
зависящая от х и n произвольных независимых постоянных , обращающая это уравнение в тождество при любых значениях . Заметим, что число произвольных постоянных равно порядку дифференциального уравнения.
Определение 7 Общее решение, заданное в неявном виде
,
называется общим интегралом.
Определение 8 Частным решением дифференциального уравнения (1) называется решение, которое получается из формулы (3), если придать определенные значения произвольным постоянным, т. е.
,
где – фиксированные числа.
Определение 9 Частным интегралом называется интеграл, полученный из общего путем фиксирования произвольных постоянных
,
где – фиксированные числа.
В некоторых случаях дифференциальное уравнение может не иметь решения. Поэтому есть ряд теорем существования, которые накладывают условия на правую часть дифференциального уравнения, при выполнении которых решение существует.
Общий вид дифференциального уравнения первого порядка:
| . | (4) |
Если это уравнение разрешимо относительно , то
| . | (5) |
Следовательно, общим решением дифференциального уравнения (4) называется функция
,
зависящая от х и произвольной постоянной С, обращающая это уравнение в тождество.
Общее решение, заданное в неявном виде
,
называется общим интегралом.
Геометрически общее решение представляет собой семейство интегральных кривых на плоскости, зависящих от одного параметра С. Частное решение и частный интеграл имеют соответственно вид:
; .
Уравнение имеет бесконечное число решений. Чтобы из этого множества решений выделить одно, т. е. частное решение, надо задать некоторые дополнительные условия. Таким условием, определяющим частное решение, является начальное условие, или условие Коши:
| , | (6) |
где х0 – заданный элемент из области определения.
Задача отыскания частного решения уравнения (5), удовлетворяющего начальному условию (6), называется задачей Коши для этого уравнения.
Рассмотрим простейшее дифференциальное уравнение первого порядка
| , | (7) |
где – непрерывная на некотором промежутке функция.
Решение ОДУ (7) находится интегрированием его левой и правой частей:
.
Пример 1Решить уравнение и построить семейство интегральных кривых.
Решение. – общее решение данного уравнения, где С = const.
Задавая конкретные значения постоянной С, будем иметь частные решения исходного уравнения.
Таким образом, интегральные кривые – это множество парабол. Построим их:
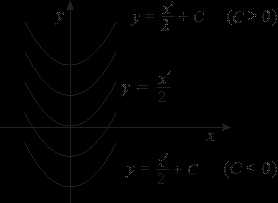
Если для данного уравнения задана задача Коши, т. е. необходимо найти решение исходного уравнения, удовлетворяющего начальному условию, например:
,
то для ее решения необходимо в общее решение задачи вместо х и у подставить , и найти конкретное значение произвольной постоянной С. Так как , то .
Следовательно, решением данной задачи Коши будет функция
.
Заметим, что график этой функции проходит через точку .
С геометрической точки зрения, решить задачу Коши – значит, из бесконечного множества интегральных кривых найти ту, которая проходит через точку с координатами .
Пример 2Решить задачу Коши
, .
Решение:
;
– общее решение данного уравнения.
Для решения задачи Коши найдем константу С. Подставим в общее решение , :
.
Таким образом, решением задачи Коши будет функция
.
Следовательно, интегральная кривая имеет вид:
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
zdamsam.ru
Конспект лекции_6 Дифференциальные уравнения первого порядка
Учреждение образования «Белорусская государственная
сельскохозяйственная академия»
Кафедра высшей математики
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Конспект лекции для студентов бухгалтерского факультета
заочной формы получения образования (НИСПО)
Горки, 2013
Дифференциальные уравнения первого порядка
Понятие дифференциального уравнения. Общее и частное решения
При изучении различных явлений часто не удаётся найти закон, который непосредственно связывает независимую переменную и искомую функцию, но можно установить связь между искомой функцией и её производными.
Соотношение, связывающее независимую переменную, искомую функцию и её производные, называется дифференциальным уравнением:
. (1)
Здесь x – независимая переменная, y – искомая функция, – производные искомой функции. При этом в соотношении (1) обязательно наличие хотя бы одной производной.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.
Рассмотрим дифференциальное уравнение
. (2)
Так в это уравнение входит производная только первого порядка, то оно называется дифференциальным уравнением первого порядка.
Если уравнение (2) можно разрешить относительно производной и записать в виде
, (3)
то такое уравнение называется дифференциальным уравнением первого порядка в нормальной форме.
Во многих случаях целесообразно рассматривать уравнение вида
, (4)
которое называется дифференциальным уравнением первого порядка, записанным в дифференциальной форме.
Так
как 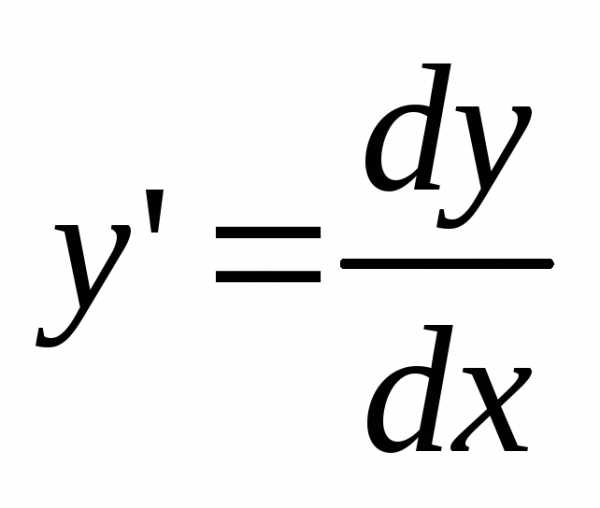 ,
то уравнение (3) можно записать в виде
,
то уравнение (3) можно записать в виде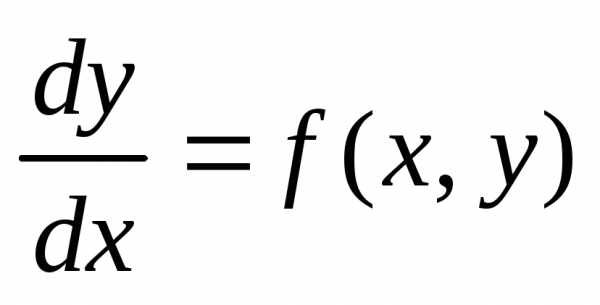 или,
где можно считатьи.
Это означает, что уравнение (3) преобразовано
в уравнение (4).
или,
где можно считатьи.
Это означает, что уравнение (3) преобразовано
в уравнение (4).
Запишем
уравнение (4) в виде
.
Тогда,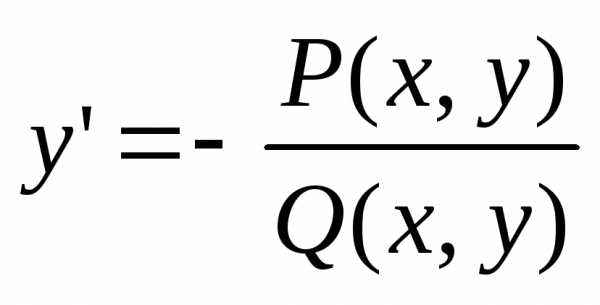 ,,
где можно считать
,,
где можно считать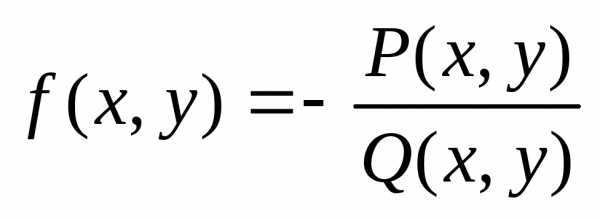 , т.е. получено уравнение вида (3). Таким
образом, уравнения (3) и (4) равносильны.
, т.е. получено уравнение вида (3). Таким
образом, уравнения (3) и (4) равносильны.
Решением
дифференциального уравнения (2) или (3) называется любая функция  ,
которая при подстановке её в уравнение
(2) или (3) обращает его в тождество:
,
которая при подстановке её в уравнение
(2) или (3) обращает его в тождество:
или .
Процесс
нахождения всех решений дифференциального
уравнения называется его интегрированием,
а график решения  дифференциального уравнения называетсяинтегральной
кривой этого уравнения.
дифференциального уравнения называетсяинтегральной
кривой этого уравнения.
Если решение дифференциального уравнения получено в неявном виде , то оно называетсяинтегралом данного дифференциального уравнения.
Общим решением дифференциального уравнения первого порядка называется семейство функций вида , зависящее от произвольной постояннойС, каждая из которых является решением данного дифференциального уравнения при любом допустимом значении произвольной постоянной С. Таким образом, дифференциальное уравнение имеет бесчисленное множество решений.
Частным
решением дифференциального уравнения называется
решение, получаемое из формулы общего
решения при конкретном значении
произвольной постоянной С,
включая  .
.
Задача Коши и её геометрическая интерпретация
Уравнение (2) имеет бесчисленное множество решений. Чтобы из этого множества выделить одно решение, которое называется частным, нужно задать некоторые дополнительные условия.
Задача отыскания частного решения уравнения (2) при заданных условиях называется задачей Коши. Эта задача является одной из важнейших в теории дифференциальных уравнений.
Формулируется
задача Коши следующим образом: среди
всех решений уравнения (2) найти такое
решение 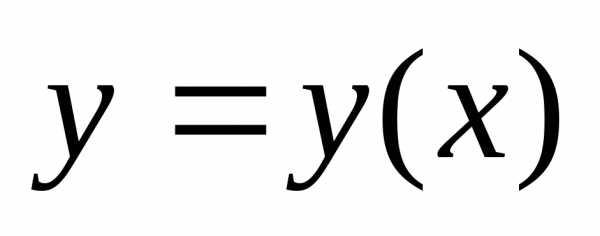 ,
в котором функция
,
в котором функция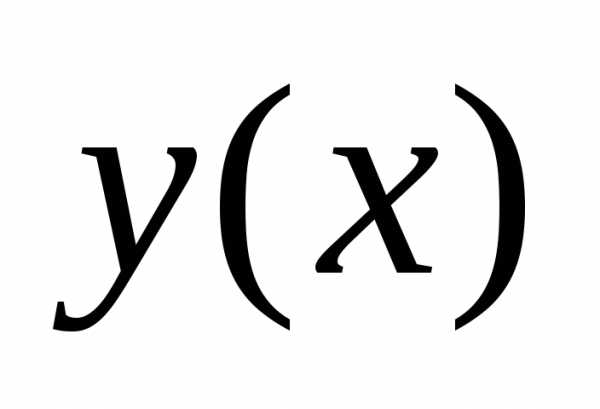 принимает заданное числовое значение
принимает заданное числовое значение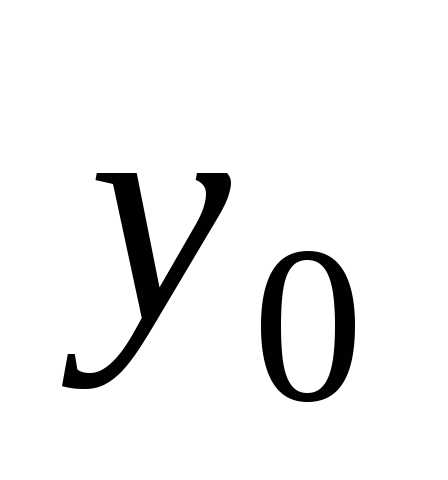 ,
если независимая переменнаяx принимает заданное числовое значение
,
если независимая переменнаяx принимает заданное числовое значение 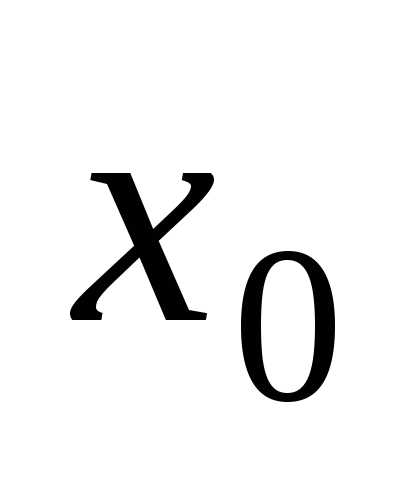 ,
т.е.
,
т.е.
, , (5)
где D – область определения функции 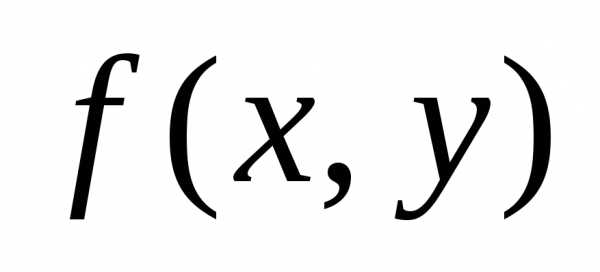 .
.
Значение 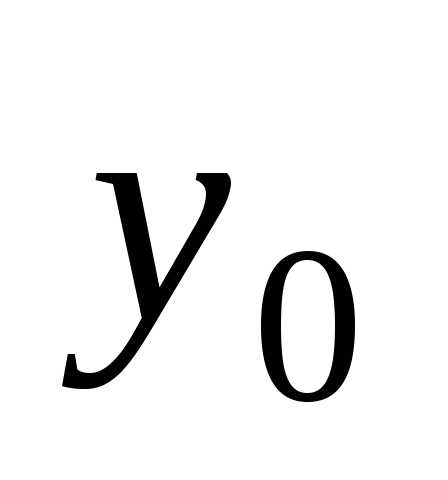 называетсяначальным
значением функции,
а
называетсяначальным
значением функции,
а 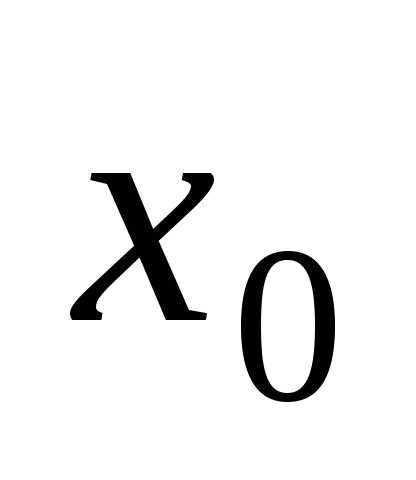 – начальным
значением независимой переменной.
Условие (5) называется начальным
условием или условием
Коши.
– начальным
значением независимой переменной.
Условие (5) называется начальным
условием или условием
Коши.
С геометрической точки зрения задачу Коши для дифференциального уравнения (2) можно сформулировать следующим образом: из множества интегральных кривых уравнения (2) выделить ту, которая проходит через заданную точку .
Дифференциальные уравнения с разделяющимися переменными
Одним из простейших видов дифференциальных уравнений является дифференциальное уравнение первого порядка, не содержащее искомой функции:
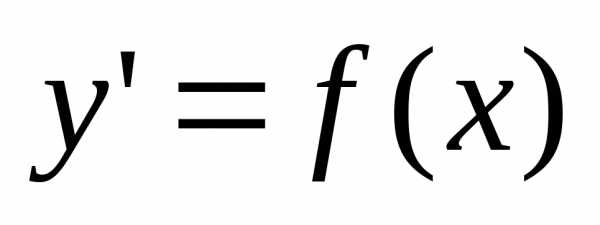 .
(6)
.
(6)
Учитывая,
что 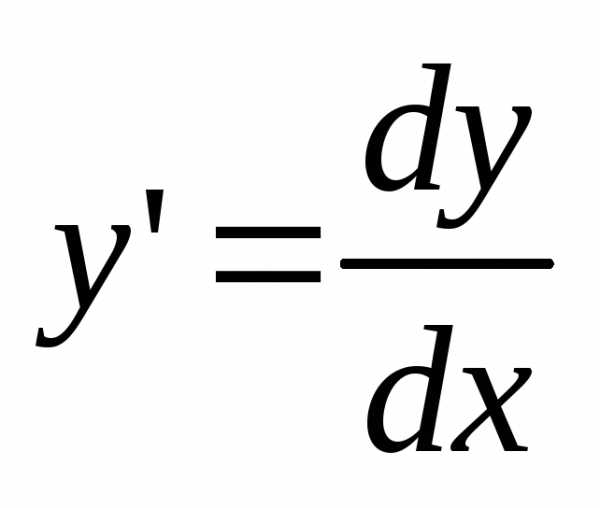 ,
запишем уравнение в виде
,
запишем уравнение в виде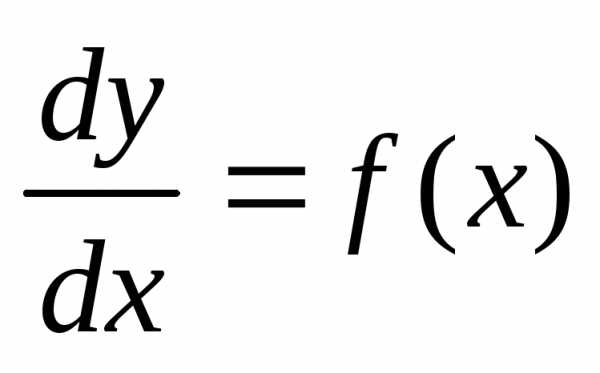 или.
Интегрируя обе части последнего
уравнения, получим:или
или.
Интегрируя обе части последнего
уравнения, получим:или
 .
(7)
.
(7)
Таким образом, (7) является общим решением уравнения (6).
Пример 1. Найти общее решение дифференциального уравнения .
Решение.
Запишем уравнение в виде 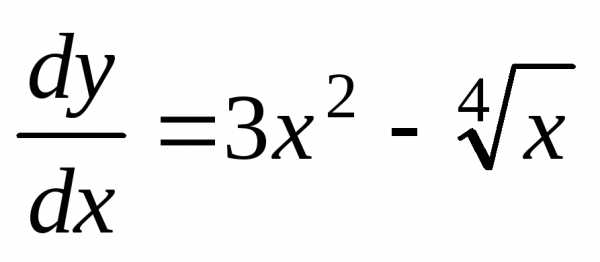 или
или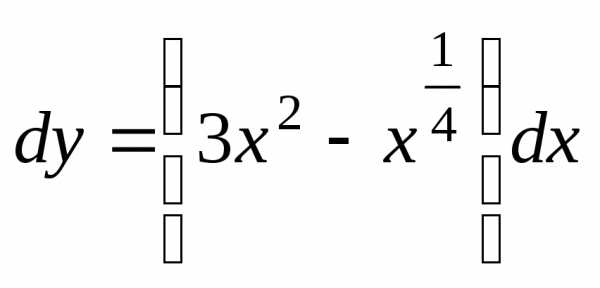 .
Проинтегрируем обе части полученного
уравнения:
.
Проинтегрируем обе части полученного
уравнения: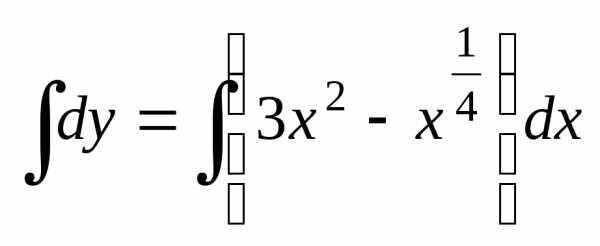 ,
, .
Окончательно запишем
.
Окончательно запишем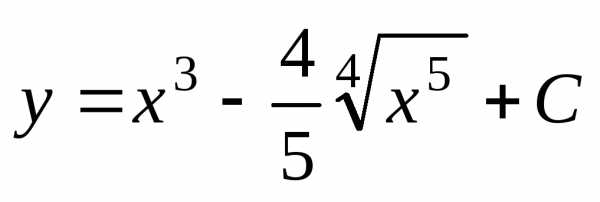 .
.
Пример
2.
Найти решение уравнения  при условии
при условии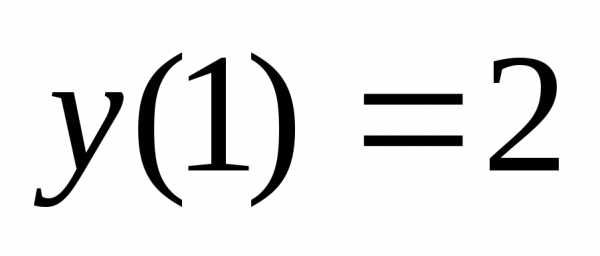 .
.
Решение.
Найдём общее решение уравнения: 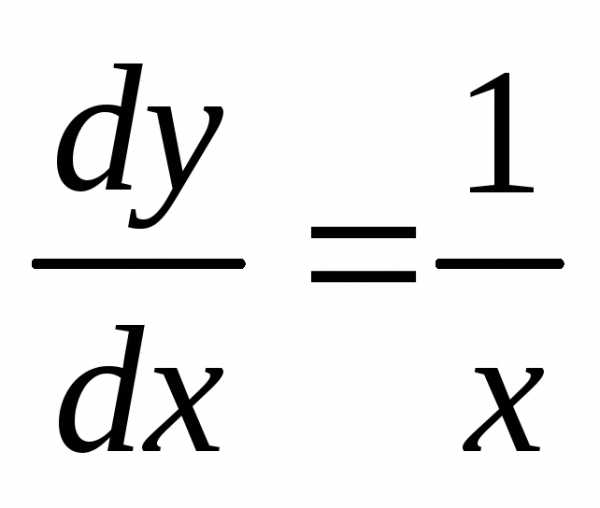 ,
,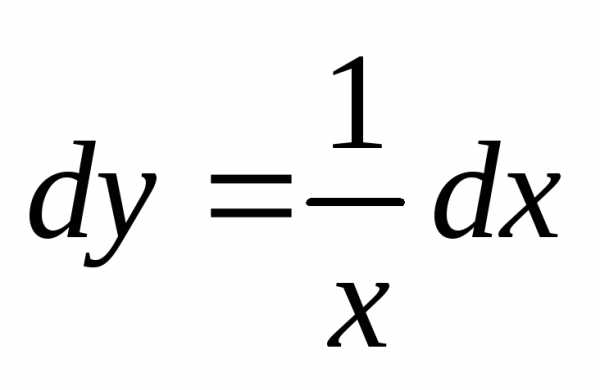 ,
,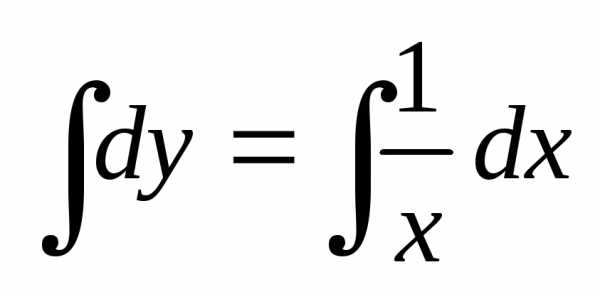 ,.
По условию
,.
По условию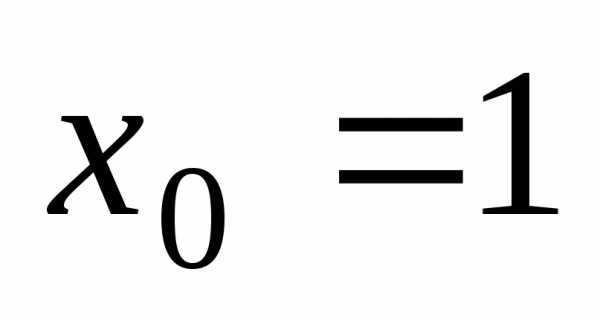 ,
,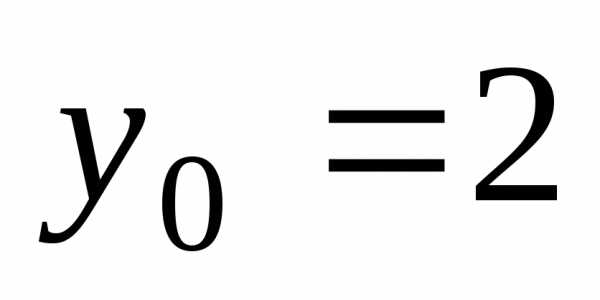 .
Подставим в общее решение:или
.
Подставим в общее решение:или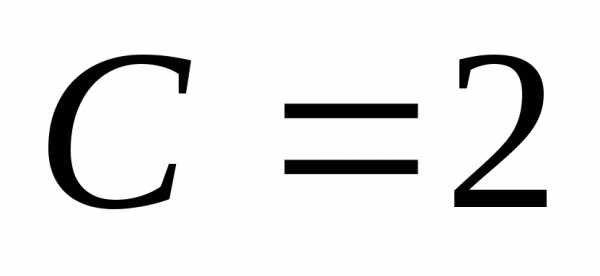 .
Найденное значение произвольной
постоянной подставим в формулу общего
решения:
.
Найденное значение произвольной
постоянной подставим в формулу общего
решения: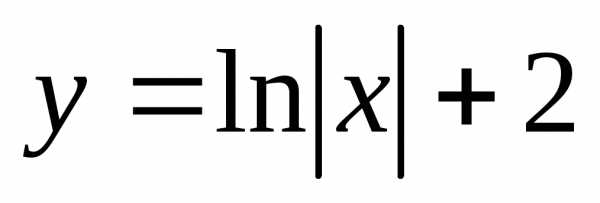 .
Это и есть частное решение дифференциального
уравнения, удовлетворяющее заданному
условию.
.
Это и есть частное решение дифференциального
уравнения, удовлетворяющее заданному
условию.
Уравнение
 (8)
(8)
Называется дифференциальным
уравнением первого порядка, не содержащим
независимой переменной.
Запишем его в виде  или
или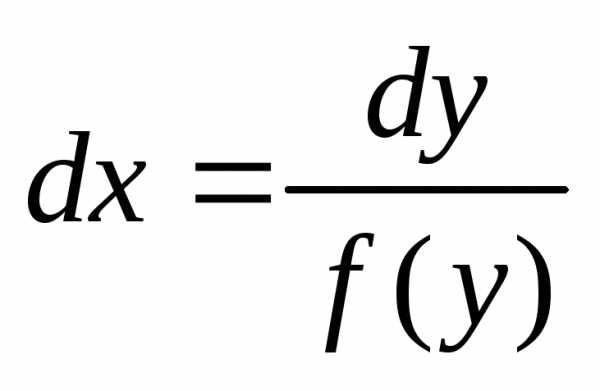 .
Проинтегрируем обе части последнего
уравнения:
.
Проинтегрируем обе части последнего
уравнения: или
или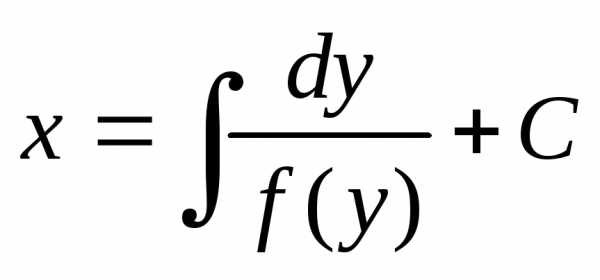 – общее решение уравнения (8).
– общее решение уравнения (8).
Пример.
Найти общее решение уравнения  .
.
Решение.
Запишем это уравнение в виде:  или
или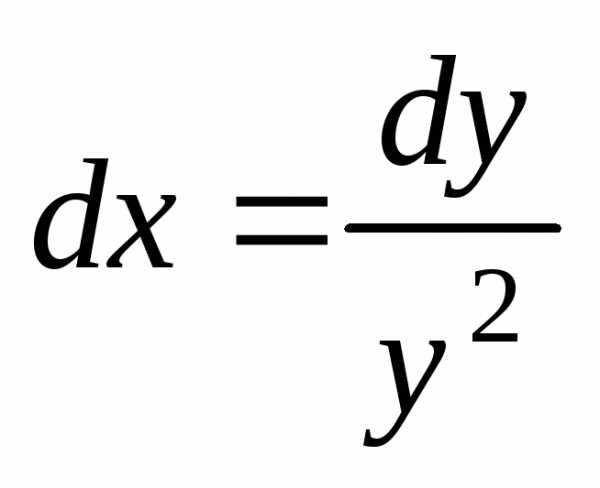 .
Тогда
.
Тогда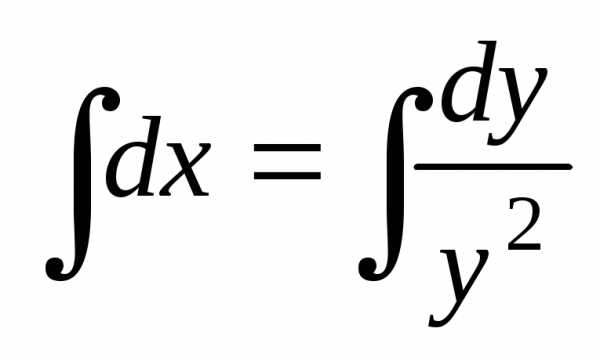 ,
,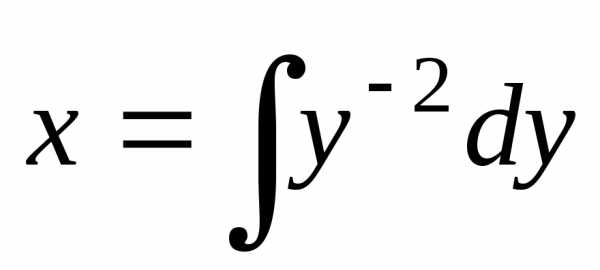 ,
,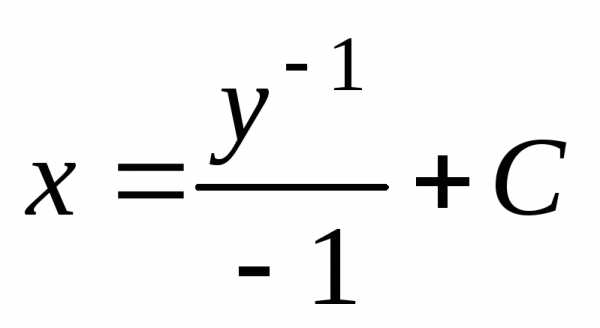 ,
,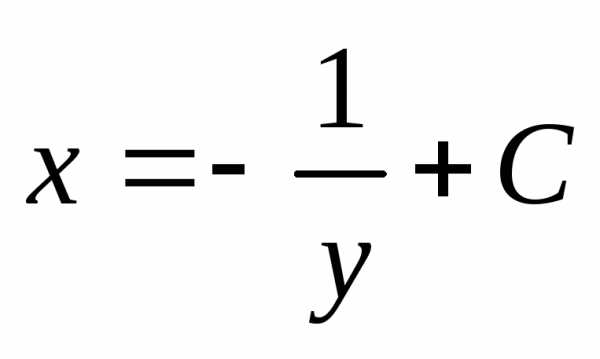 .
Таким образом,
.
Таким образом,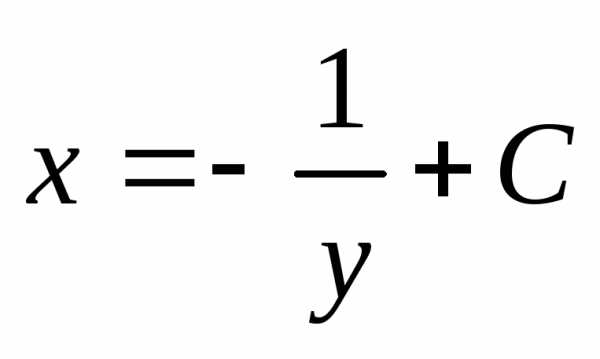 – общее решение данного уравнения.
– общее решение данного уравнения.
Уравнение вида
(9)
интегрируется
с помощью разделения переменных. Для
этого уравнение запишем в виде 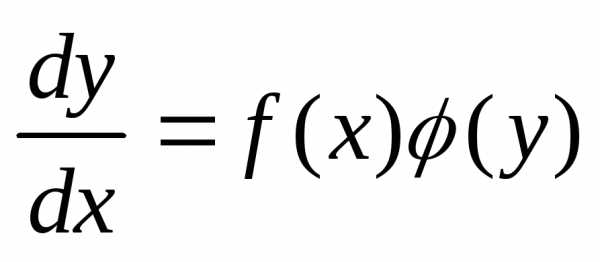 ,
а затем с помощью операций умножения и
деления приводим его к такой форме,
чтобы в одну часть входила только функция
отх и дифференциал dx,
а во вторую часть – функция от у и дифференциал dy.
Для этого обе части уравнения нужно
умножить на dx и разделить на
,
а затем с помощью операций умножения и
деления приводим его к такой форме,
чтобы в одну часть входила только функция
отх и дифференциал dx,
а во вторую часть – функция от у и дифференциал dy.
Для этого обе части уравнения нужно
умножить на dx и разделить на  .
В результате получим уравнение
.
В результате получим уравнение
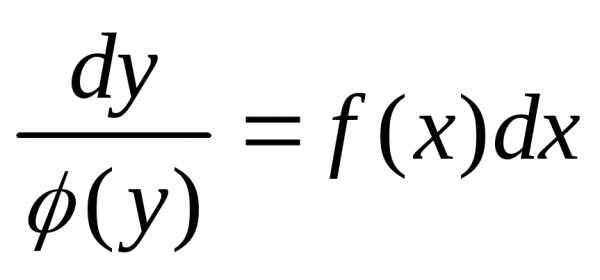 ,
(10)
,
(10)
в котором переменные х и у разделены. Проинтегрируем обе части уравнения (10): . Полученное соотношение является общим интегралом уравнения (9).
Пример 3. Проинтегрировать уравнение .
Решение.
Преобразуем уравнение и разделим
переменные:  ,
,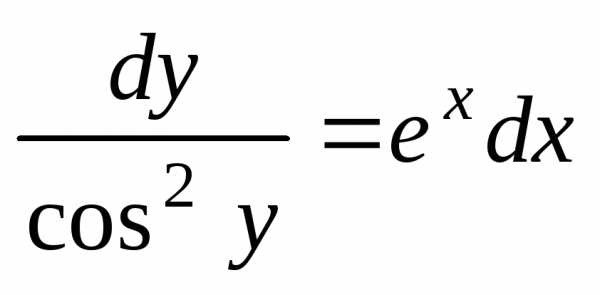 .
Проинтегрируем:
.
Проинтегрируем: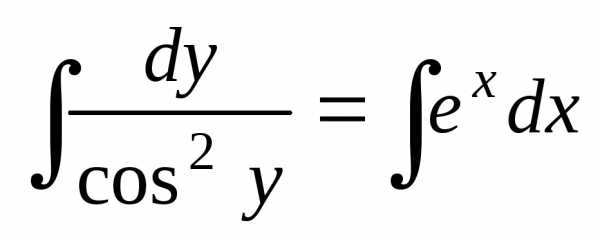 ,или – общий интеграл данного уравнения..
,или – общий интеграл данного уравнения..
Пусть уравнение задано в виде
. (11)
Такое уравнение называется дифференциальным уравнением первого порядка с разделяющимися переменными в симметрической форме.
Для разделения переменных нужно обе части уравнения разделить на :
. (12)
Полученное уравнение называется дифференциальным уравнением с разделёнными переменными. Проинтегрируем уравнение (12):
. (13)
(13)
Соотношение (13) является общим интегралом дифференциального уравнения (11).
Пример 4. Проинтегрировать дифференциальное уравнение .
Решение. Запишем уравнение в виде
и
разделим обе его части на 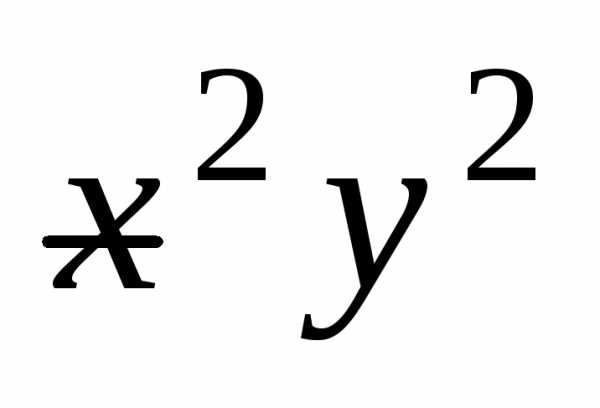 ,.
Полученное уравнение:
,.
Полученное уравнение: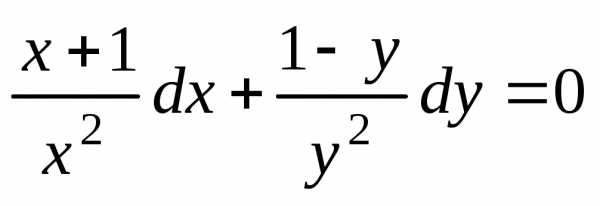 является уравнением с разделёнными
переменными. Проинтегрируем его:
является уравнением с разделёнными
переменными. Проинтегрируем его:
, ,
, . Последнее равенство является общим интегралом данного дифференциального уравнения.
Пример
5.
Найти частное решение дифференциального
уравнения
,
удовлетворяющее условию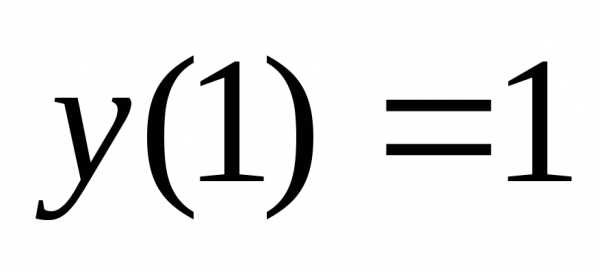 .
.
Решение.
Учитывая, что  ,
запишем уравнение в виде
,
запишем уравнение в виде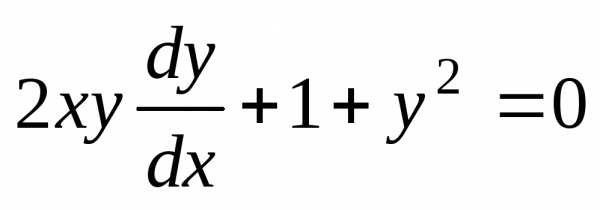 или.
Разделим переменные:
или.
Разделим переменные: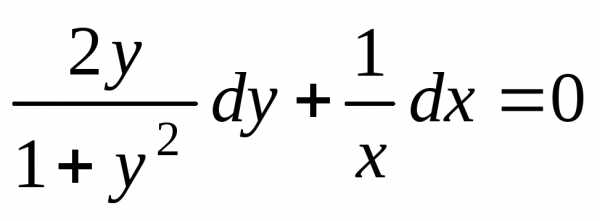 .
Проинтегрируем это уравнение:,,.
Полученное соотношение является общим
интегралом данного уравнения. По условию.
Подставим в общий интеграл и найдёмС:
,С=1.
Тогда выражение
является частным решением данного
дифференциального уравнения, записанным
в виде частного интеграла.
.
Проинтегрируем это уравнение:,,.
Полученное соотношение является общим
интегралом данного уравнения. По условию.
Подставим в общий интеграл и найдёмС:
,С=1.
Тогда выражение
является частным решением данного
дифференциального уравнения, записанным
в виде частного интеграла.
Линейные дифференциальные уравнения первого порядка
Уравнение
(14)
называется линейным
дифференциальным уравнением первого
порядка.
Неизвестная функция  и её производная входят в это уравнение
линейно, а функции
и её производная входят в это уравнение
линейно, а функции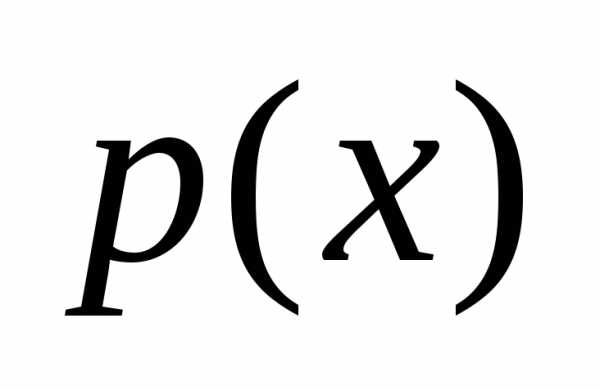 и
и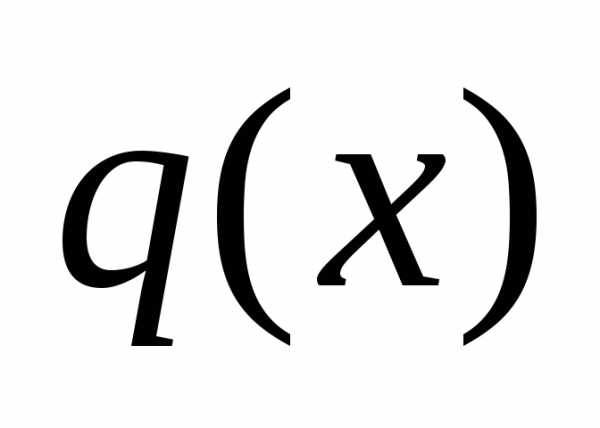 непрерывны.
непрерывны.
Если 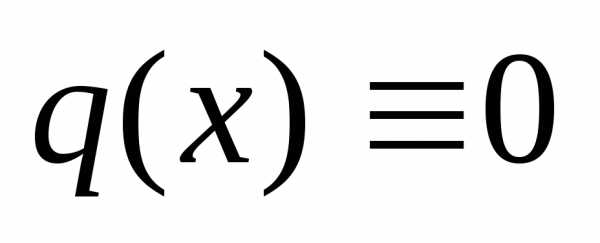 ,
то уравнение
,
то уравнение
(15)
называется линейным
однородным.
Если 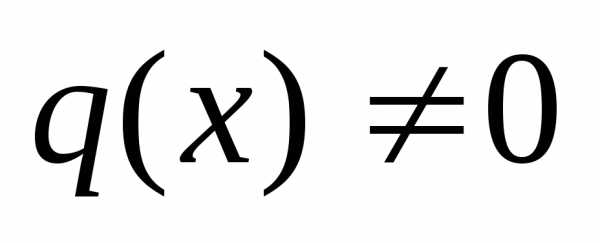 ,
то уравнение (14) называетсялинейным
неоднородным.
,
то уравнение (14) называетсялинейным
неоднородным.
Для нахождения решения уравнения (14) обычно используют метод подстановки (Бернулли), суть которого в следующем.
Решение уравнения (14) будем искать в виде произведения двух функций
, (16)
где  и
и –
некоторые непрерывные функции. Подставим
–
некоторые непрерывные функции. Подставим и производнуюв уравнение (14):
и производнуюв уравнение (14):
или
Функцию v будем подбирать таким образом, чтобы выполнялось условие . Тогда. Таким образом, для нахождения решения уравнения (14) нужно решить систему дифференциальных уравнений
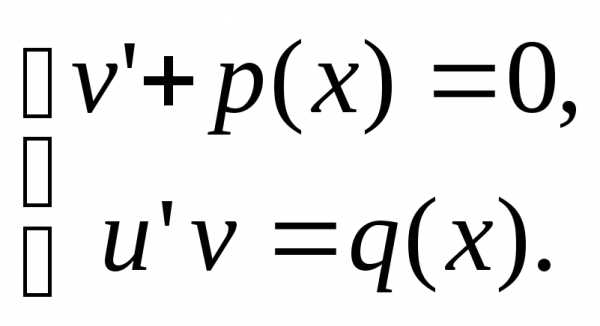
Первое
уравнение системы является линейным
однородным уравнением и решить его
можно методом разделения переменных: 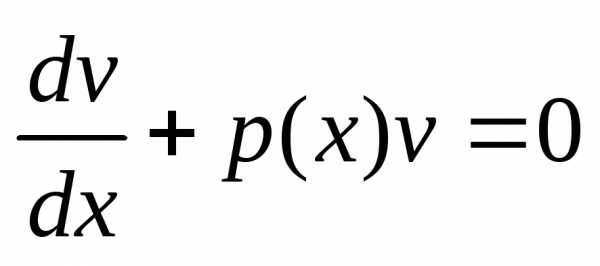 ,
,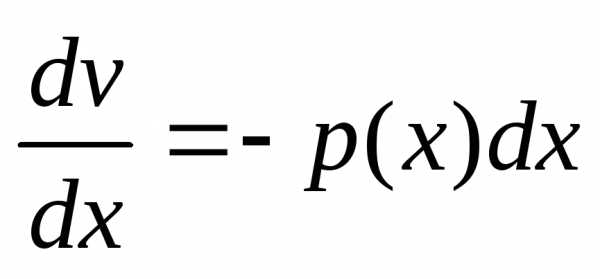 ,
,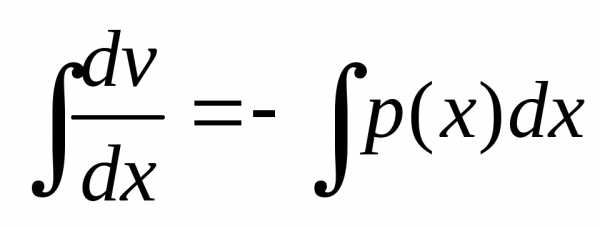 ,,.
В качестве функции
,,.
В качестве функции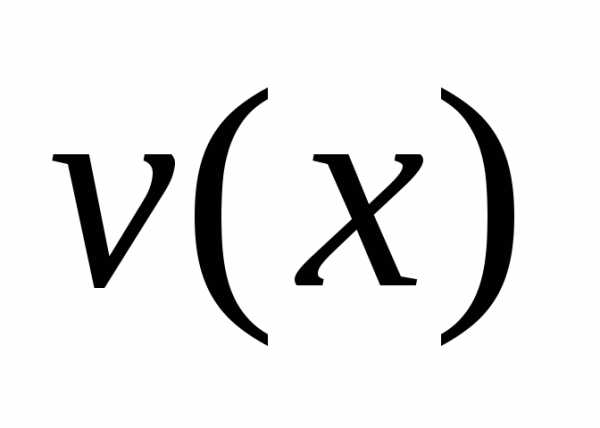 можно
взять одно из частных решений однородного
уравнения, т.е. приС=1:
можно
взять одно из частных решений однородного
уравнения, т.е. приС=1: 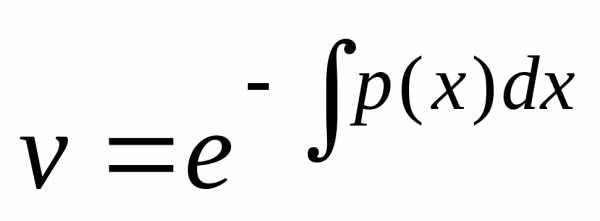 .
Подставим во второе уравнение системы:или.Тогда.
Таким образом, общее решение линейного
дифференциального уравнения первого
порядка имеет вид.
.
Подставим во второе уравнение системы:или.Тогда.
Таким образом, общее решение линейного
дифференциального уравнения первого
порядка имеет вид.
Пример
6.
Решить уравнение  .
.
Решение.
Решение уравнения будем искать в виде 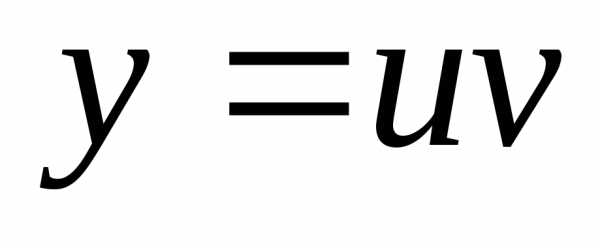 .
Тогда.
Подставим в уравнение:
.
Тогда.
Подставим в уравнение:
или
.
Функциюv выберем таким образом, чтобы выполнялось
равенство 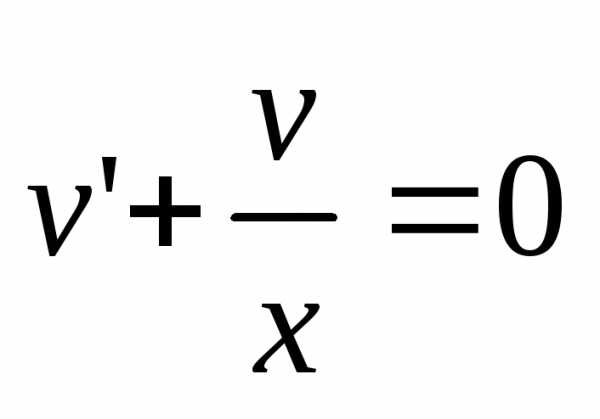 .
Тогда
.
Тогда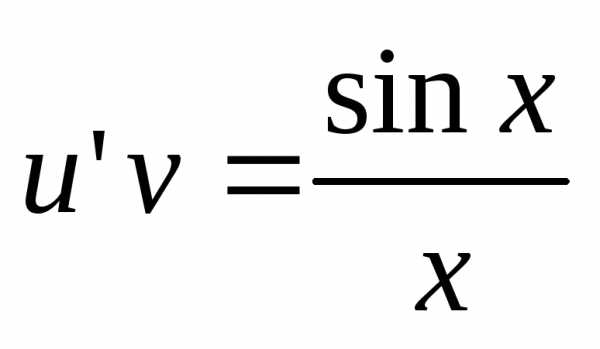 .
Решим первое из этих уравнений методом
разделения переменных:
.
Решим первое из этих уравнений методом
разделения переменных: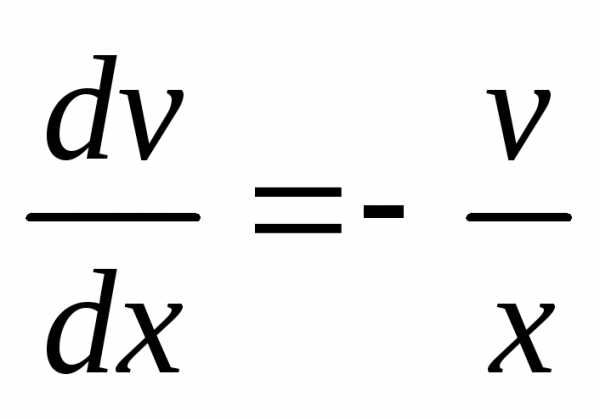 ,
,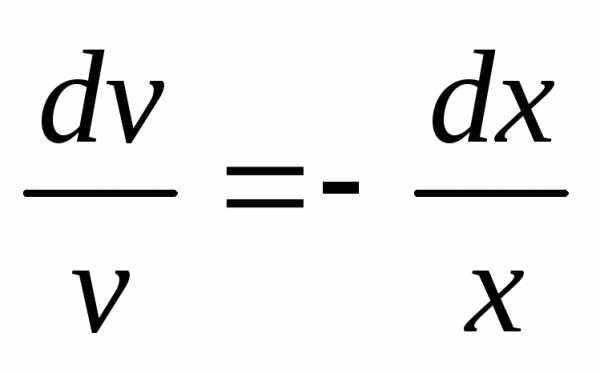 ,
,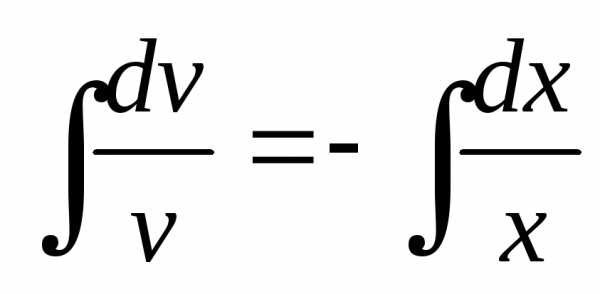 ,,
,,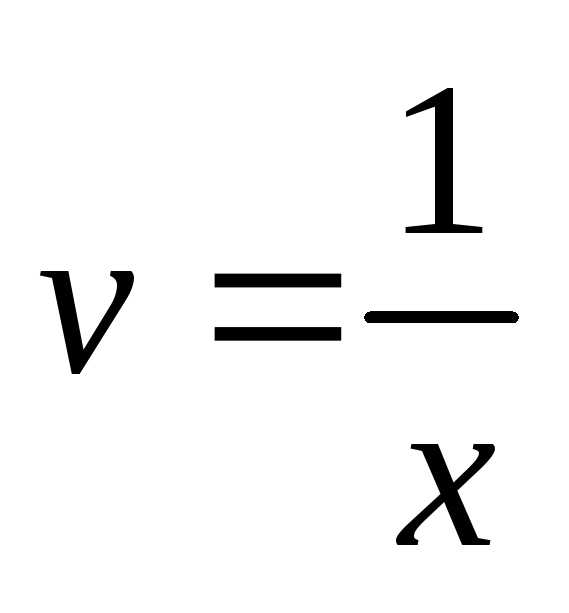 .
Функциюv подставим во второе уравнение:
.
Функциюv подставим во второе уравнение: 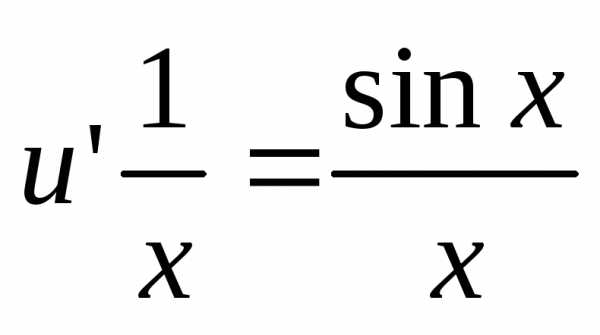 ,,
,,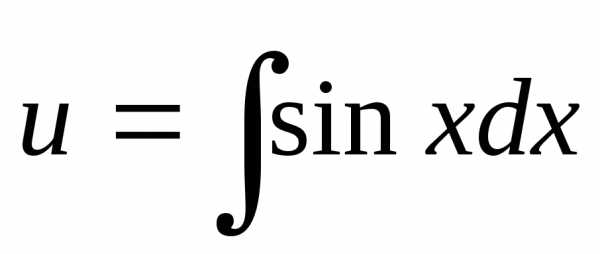 ,.
Общим решением данного уравнения
является
,.
Общим решением данного уравнения
является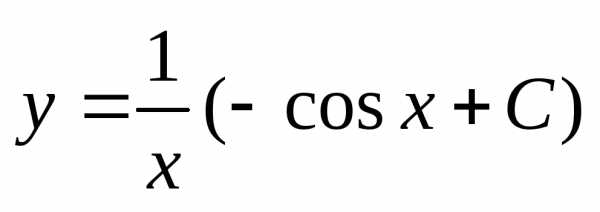 .
.
Вопросы для самоконтроля знаний
Что называется дифференциальным уравнением?
Что называется порядком дифференциального уравнения?
Какое дифференциальное уравнение называется дифференциальным уравнением первого порядка?
Как записывается дифференциальное уравнение первого порядка в дифференциальной форме?
Что называется решением дифференциального уравнения?
Что называется интегральной кривой?
Что называется общим решением дифференциального уравнения первого порядка?
Что называется частным решением дифференциального уравнения?
Как формулируется задача Коши для дифференциального уравнения первого порядка?
Какова геометрическая интерпретация задачи Коши?
Как записывается дифференциальное уравнение с разделяющимися переменными в симметрической форме?
Какое уравнение называется линейным дифференциальным уравнением первого порядка?
Каким методом можно решить линейное дифференциальное уравнение первого порядка и в чём суть этого метода?
Задания для самостоятельной работы
Решить дифференциальные уравнения с разделяющимися переменными:
а) ; б);
в) ; г).
2. Решить линейные дифференциальные уравнения первого порядка:
а) 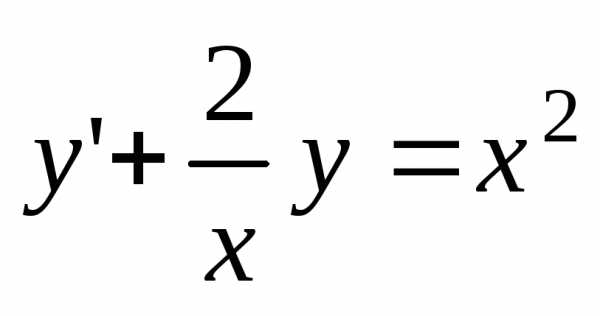 ;
б);
в)
;
б);
в)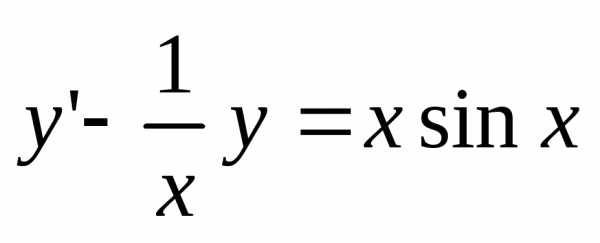 ;
;
г)
;
д)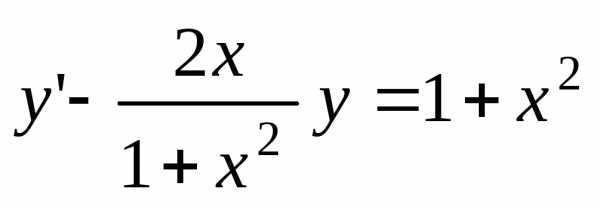 .
.
12
studfiles.net
59.Задача Коши, начальные условия. Теорема существования и единственности решения задачи Коши для уравнения . Особые точки. Особые решения. Примеры.
http://www.nsc.ru/rus/textbooks/akhmerov/ode_unicode/m-21/m-21.html
НАЧАЛЬНЫЕ УСЛОВИЯ
– условия при постановке задачи Коши для дифференциальных уравнений. Для обыкновенного дифференциального уравнения, разрешенного относительно старшей производной:
Н. у. состоят в задании производных (данных Коши)
где – произвольная фиксированная точка области определения функции F;эта точка наз. начальной точкой искомого решения. Задачу Коши (1), (2) часто наз. также начальной задачей.
Для дифференциального уравнения с частными производными, записанного в нормальной форме относительно выделенной переменной V.
Н. у. состоят в задании производных (данные Коши):
от искомого решения и( х, t )этого уравнения на гиперплоскости t=0 (носителя начальных условий).
60.Уравнение 1-го порядка с разделяющимися переменными.
Уравнением с разделенными переменными называется дифференциальное уравнение вида
f(x)dx + g(y)dy = 0
с непрерывными функциями f(х) и g(y).
Равенство
где C — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.
Начальное условие для уравнения f(x)dx + g(y)dy = 0 можно задавать в виде y(x0) = y0 или в виде x(y0) = x0 .
Уравнением с разделяющимися переменными называется дифференциальное уравнение вида
f1(x)g1 (y)dx + f2(x) g2(y)dy =0 .
Функции f1(x), g1(y), f2(x), g2(y) непрерывны в cвоих областях определения и g1(y)f2(x) ≠ 0 .
Разделив обе части уравнения на отличное от нуля произведение g1(y)f2(x), получим уравнение с разделенными переменными
Общий интеграл этого уравнения имеет вид
Решение уравнения в области, где g1(y)f2(x) = 0 требует специального обсуждения.
61. Однородное уравнение 1-го порядка. Определение однородной функции
Определение однородного дифференциального уравнения
Дифференциальное уравнение первого порядка
называется однородным, если правая часть удовлетворяет соотношению
для всех значений t. Другими словами, правая часть должна являться однородной функцией нулевого порядка по отношению к переменным x и y:
Однородное дифференциальное уравнение можно также записать в виде
или через дифференциалы:
где P(x,y) и Q(x,y) − однородные функции одинакового порядка.
Определение однородной функции
Функция P(x,y) называется однородной функцией порядка n, если для всех t > 0 справедливо следующее соотношение:
Решение однородных дифференциальных уравнений
Однородное дифференциальное уравнение можно решить с помощью подстановки y = ux, которая преобразует однородное уравнение в уравнение с разделяющимися переменными. Дифференциальное уравнение вида
преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной:
62. Линейное уравнение 1-го порядка. Методы решения: метод Лагранжа, метод Бернулли. Структура решения линейного уравнения.
Линейным дифференциальным уравнением первого порядка называется уравнение вида
Здесь a(x) и b(x) — известные, непрерывные на [a;b] функции.
Доказано, что если функции a(x) и b(x) непрерывны на [a;b] , то для любой начальной точки (x0, y0) , x0∈ [a; b] , задача Коши
имеет единственное решение y = y(x) на [a;b].
Рассматривают однородные и неоднородные линейные уравнения первого порядка:
Общее решение линейного уравнения 1-го порядка можно найти с помощью замены y(x) = u(x) · v(x) .
studfiles.net