Сила притяжения что такое – Что такое сила притяжения
Что такое сила притяжения
Когда на уроках физики в начальных классах преподаватель упоминает существовавшее ранее представление о планете Земле как о плоскости, покоящейся на китах, слонах или черепахах, то на лицах учеников появляются улыбки и в классе даже раздаются смешки. Это сейчас многие уже в детском садике знают, что Земля – это шар, а сила притяжения воздействует на все материальные предметы. Однако давайте хотя бы на мгновение представим, что о гравитации нам ничего не известно. Как тогда объяснить, что люди удерживаются на поверхности, а вода океанов не изливается в пустоту космического пространства, если не воспользоваться представлением о плоской планете? Если сила притяжения для нас тайна – то, пожалуй, никак. Именно поэтому так важно относится с пониманием к прошлому, ведь каждому времени – свои открытия.
Сила гравитационного притяжения была открыта И. Ньютоном в 1666 году. До него тяготение пытались объяснить такие выдающиеся ученые своего времени, как Гюйгенс, известный своими трудами по центробежной силе, Декарт, а также Кеплер, сформулировавший фундаментальные три закона, которым подчиняется перемещение небесных объектов. Однако это были лишь предположения, основывающиеся скорее на догадках, а не на фактах. Ни одно из них не давало целостного понимания мироустройства. Ньютон же намеревался создать завершенную теорию, в рамках которой могла быть объяснена сила притяжения и взаимосвязанные с ней явления. И это ему удалось. Были сформулированы не просто теоретические предпосылки с формулами, а создана полноценная модель. Она оказалась настолько удачной, что даже сейчас, спустя столетия, общая теория относительности, будучи развитием идей Ньютона, используется при расчетах небесной механики.
Ее формулировка крайне простая и запоминающаяся: сила, с которой объекты притягиваются, зависит от их массы и расстояния. Данное определение выражается следующим образом:
F = (M1*M2) / (R*R),
где M1 и M2 – массы объектов; R – расстояние.
Обычно знакомство с классической теорией начинают именно с этой формулы. Для более точного представления всю правую часть следует умножить на гравитационную константу.
Вывод следующий: чем объект массивнее, тем более сильное притягивающее воздействие он оказывает на окружение. При этом совершенно не принципиально, будет ли это сфера массой 1 кг, или точка с таким же весом. В то же время, при расчете системы двух тел, например, Солнца и Земли, последняя точно так же притягивает звезду к себе. Сила притяжения земли, взаимодействующая с полем Солнца, формирует общий центр масс, вокруг которого происходит взаимное обращение. Это только кажется, что Солнце – центр нашей системы. Истинный же, хотя и находится в звезде, с физической серединной точкой не совпадает.
Сила притяжения может быть определена в рамках классического закона всемирного тяготения при соблюдении двух условий:
– скорости объектов рассматриваемой системы значительно меньше скорости луча света;
– потенциал гравитационного поля относительно мал.
В скором времени после завершения Ньютоном работ по притяжению, стала очевидной необходимость ее существенной доработки. Дело в том, что хотя движение тел небесной сферы можно было рассчитывать с помощью предложенных формул, иногда возникали ситуации, когда теория Ньютона оказывалась неприменимой, так как давала совершенно непредсказуемые результаты.
Недостатки были устранены Эйнштейном, предложившим серьезно доработанную модель, учитывающую как скорость света, так и слишком сильные гравитационные поля. Однако сейчас даже такая общая теория относительности перестала быть универсальным ответом на все вопросы: в микромире ее постулаты оказываются неверны.
fb.ru
Ответы@Mail.Ru: Что такое сила притяжения?
МЕХАНИЗМ ПРИТЯЖЕНИЯ (ГРАВИТАЦИИ). СИЛА ПРИТЯЖЕНИЯМеханизм притяжения основан на первом принципе поведения эфира – «В эфирном поле не возникает эфирных пустот». Эфир, заполняющий силовой центр частицы, а вместе с ним и сам силовой центр частицы движутся в направлении недостатка эфира, возникающего в том месте эфирного поля, где располагается объект, обладающий Полем Притяжения – т.е. у которого количество исчезающего эфира преобладает над количеством творимого. При этом неважно, каким качеством обладает сама притягиваемая частица – она может иметь как Поле Притяжения, так и Поле Отталкивания, и величина этих Полей может быть любой. В любом случае заполняющий ее эфир будет двигаться в направлении недостатка – т.е. в составе эфирного потока Поля Притяжения «притягивающего» ее объекта.
Стремление эфира, заполняющего притягиваемую частицу, двигаться в направлении недостатка эфира – т.е. объекта с Полем Притяжения – называется «Силой Притяжения».
Когда частица, двигаясь в Поле Притяжения другой частицы, сближается и соприкасается с ней, она останавливается – между частицами возникает связь. Можно назвать ее гравитационной, т.е. обусловленной действием Поля Притяжения. Не существует ни химических, ни ядерных, ни каких-либо еще видов связи. Любой тип связи является гравитационным, т.е. существующим благодаря действию Поля Притяжения. Возникновение связи между частицами можно иначе назвать фиксацией частиц друг с другом.
Процесс притяжения можно сравнить со сматыванием нити. Если обе частицы обладают Полями Притяжения, тогда клубки расположены сразу на обоих концах нити, и они оба наматывают на себя нить одновременно, каждый со своей стороны. «Нить» в данном случае – это эфир, а «клубки» – это частицы. Когда «клубки» полностью сматывают свободную «нить» между собой, они соприкасаются друг с другом и останавливаются. В данном случае оба клубка наматывают нить, т.е. оба обладают Полем Притяжения. Но может быть и так, что только один из клубков наматывает на себя нить, в то время как другой ее только разматывает – т.е. только одна из частиц обладает Полем Притяжения, в то время как другая имеет Поле Отталкивания. Естественно, что клубки-частицы с Полями Притяжения способны наматывать на себя нить-эфир бесконечно, не изменяя при этом своего размера, так же как клубки-частицы с Полями Отталкивания способны бесконечно ее с себя сматывать (тоже не изменяя величину радиуса). Так и осуществляется процесс притяжения частицами других частиц.
Таким образом, даже после соприкосновения притягивающихся частиц, они продолжают стремиться друг по направлению к другу, так как эфир, заполняющий каждую из частиц в каждый момент времени, продолжает стремиться в направлении соседней частицы, где формируется недостаток эфира. Как уже говорилось, стремление частицы двигаться вместе с заполняющим ее эфиром – это Сила (в данном случае, Сила Притяжения).
Сила Притяжения может возникать в частицах любого качества. Давайте рассмотрим детали механизма гравитации на примере частиц разного качества. Проводимый нами мысленный эксперимент будет протекать в идеальных условиях – т.е. в абсолютно пустом пространстве. Одна из взаимодействующих частиц обязательно обладает Полем Притяжения.
1) Обе взаимодействующие частицы обладают Полями Притяжения.
А) Величина Полей Притяжения обеих частиц одинакова.
В этом случае каждая из частиц является одновременно и притягивающей, и притягиваемой. В каждой из частиц возникает Сила Притяжения, заставляющая ее сближаться со второй частицей.
В данном случае каждая из частиц находится в составе эфирного полотна. И это эфирное полотно стягивается с обеих сторон, и обе частицы движутся в его составе. И каждая из них подчиняется при этом первому принципу поведения эфира – «В эфирном поле не возникает эфирных пустот». В соответствии с этим принципом, с каждой из сторон возникает эфирный поток, направленный ко второй из частиц. Т.е. каждая из двух частиц создает по направлению к себе эфирный ток – Поле Притяжения. И
otvet.mail.ru
Земное притяжение. Гравитационное поле Земли
Гравитация, она же притяжение или тяготение, – это универсальное свойство материи, которым обладают все предметы и тела во Вселенной. Суть гравитации залучается в том, что все материальные тела притягивают к себе все другие тела, находящиеся вокруг.
Земное притяжение
Если гравитация – это общее понятие и качество, которым обладают все предметы во Вселенной, то земное притяжение – это частный случай этого всеобъемлющего явления. Земля притягивает к себе все материальные объекты, находящиеся на ней. Благодаря этому люди и животные могут спокойно перемещаться по земле, реки, моря и океаны – оставаться в пределах своих берегов, а воздух – не летать по бескрайним просторам Космоса, а образовывать атмосферу нашей планеты.
Возникает справедливый вопрос: если все предметы обладают гравитацией, почему Земля притягивает к себе людей и животных, а не наоборот? Во-первых, мы тоже притягиваем к себе Землю, просто, по сравнению с ее силой притяжения наша гравитация ничтожно мала. Во-вторых, сила гравитации прямо пропорционально зависит от массы тела: чем меньше масса тела, тем ниже его гравитационные силы.
Второй показатель, от которого зависит сила притяжения – это расстояние между предметами: чем больше расстояние, тем меньше действие гравитации. В том числе благодаря этому, планеты движутся на своих орбитах, а не падают друг на друга.
Примечательно, что своей сферической формой Земля, Луна, Солнце и другие планеты обязаны именно силе тяготения. Она действует в направлении центра, подтягивая к нему вещество, составляющее «тело» планеты.
Гравитационное поле Земли
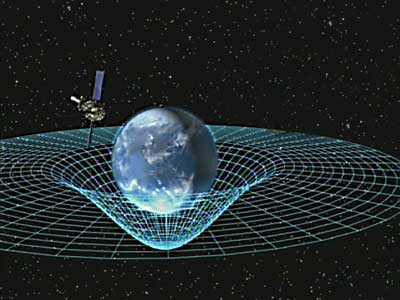
Гравитационное поле Земли – это силовое энергетическое поле, которое образуется вокруг нашей планеты благодаря действию двух сил:
- гравитации;
- центробежной силе, которая своим появление обязана вращению Земли вокруг своей оси (суточное вращение).
Поскольку и гравитация, и центробежная сила действуют постоянно, то и гравитационное поле является постоянным явлением.
Незначительное воздействие на поле оказывают силы тяготения Солнца, Луны и некоторых других небесных тел, а также атмосферных масс Земли.
Закон всемирного тяготения и сэр Исаак Ньютон

Английский физик, сэр Исаак Ньютон, согласно известной легенде, однажды гуляя по саду днем, увидел на небе Луну. В это же время с ветки упало яблоко. Ньютон тогда занимался изучением закона движения и знал, что яблоко падает под воздействием гравитационного поля, а Луна вращается по орбите вокруг Земли.
И тут в голову гениальному ученому, озаренную инсайтом, пришла мысль, что, возможно, яблоко падает на землю, подчиняясь той же силе, благодаря которой Луна находится на своей орбите, а не носится беспорядочно по всей галактике. Так был открыт закон всемирного тяготения, он же Третий закон Ньютона.
На языке математических формул этот закон выглядит так:
F = GMm/D2,
где F – сила взаимного тяготения между двумя телами;
M – масса первого тела;
m – масса второго тела;
D2 – расстояние между двумя телами;
G – гравитационная постоянная, равная 6,67х10-11.
xn—-8sbiecm6bhdx8i.xn--p1ai
Насколько велика сила притяжения? :: SYL.ru
Когда-то известнейший французский физик и астроном Араго сказал, что если бы человек не наблюдал постоянно падение тел, то сила притяжения земли была бы для него наиболее удивительным явлением. Многие вещи мы часто не замечаем только потому, что давно уже к ним привыкли. И если нам скажут, что сила гравитационного притяжения действует между любыми двумя телами, в это достаточно трудно поверить, так как в обыденной жизни мы этого попросту не видим. Почему так происходит? Вездесущие и незаметные силы гравитации
Вездесущие и незаметные силы гравитации
Почему друг к другу не притягиваются люди, машины, камни? Причина в том, что сила притяжения между небольшими предметами очень мала. Проще всего это показать на наглядном примере. Предположим, что на расстоянии в два метра друг напротив друга стоят два человека. Если принять, что у обоих из них вес средний, то сила притяжения между ними будет меньше одной сотой миллиграмма. Не всякий прибор смог бы зарегистрировать такое воздействие. По сути, оно равно такой силе, с которой гирька в 1/100 000 грамма оказывает давление на чашу весов. Поэтому понятно, что такое воздействие просто не способно сдвинуть людей с места, ведь мешает сила трения их подошв о земную поверхность, равная примерно 30% веса тела. Для того чтобы сдвинуть человека, стоящего на деревянном полу, понадобится приложить усилие не менее 20 кг. Если сравнить эту величину с одной сотой миллиграмма, то становится очевидно, что сила притяжения между разными объектами в реальной жизни ничтожно мала. Если бы не было силы трения…
Если бы не было силы трения…
Давайте немного пофантазируем. Представим себе, что сила трения вдруг перестала существовать. Что бы тогда произошло в описанном выше примере? Сила притяжения смогла бы беспрепятственно проявить себя в действии, но из-за ее малой величины сближение двух людей происходило бы очень и очень медленно. Так, в течение первых 60 минут они бы приблизились друг к другу всего лишь на 3 см, через час – еще на 9 см, а через три часа – на целых 15 см. Но, несмотря на ускорение, для того чтобы оба человека приблизились вплотную, понадобится не менее пяти часов. Перенесемся в космос
Перенесемся в космос
Мизерная в отношении малых тел сила притяжения достигает внушительных величин, если говорить о небесных телах, имеющих колоссальную массу. Так, даже такая далекая от нас планета, как Нептун, которая находится практически на самом краю нашей Солнечной системы, оказывает на Землю воздействие в целых 18 000 000 тонн! До Солнца 150 млн км. Это расстояние кажется огромным, но, если бы не сила гравитации, которая прочно удерживает нашу планету на орбите, Земля бы давно умчалась бороздить бездонные глубины мирового пространства.
Почему небесные тела не сталкиваются
Если воздействие гравитации в космосе настолько велико, то что же тогда препятствует столкновению звезд? Этот вопрос задавали еще Ньютону. В принципе, если бы небесные тела находились в неподвижном состоянии, то они рано или поздно слились бы в одну кучу. Но поскольку планеты, звезды и галактики движутся, то этого не происходит. Они словно «падают» на притягивающие их центры масс и постоянно «промахиваются», описывая при этом свои круговые или вытянутые орбиты. При этом гравитация, которая существует между ними, столь мала, что практически не мешает их движению.
www.syl.ru
Сила притяжения Википедия
 Cила тяжести mg складывается из гравитационного притяжения планеты GMm/r2 и центробежной силы инерции mω2a.
Cила тяжести mg складывается из гравитационного притяжения планеты GMm/r2 и центробежной силы инерции mω2a.Си́ла тя́жести — сила, действующая на любое физическое тело, находящееся вблизи поверхности Земли или другого астрономического тела.
По определению, сила тяжести на поверхности планеты складывается из гравитационного притяжения планеты и центробежной силы инерции, вызванной суточным вращением планеты[1][2].
Остальные силы (например, притяжение Луны и Солнца) ввиду их малости не учитывают или изучают отдельно как временные изменения гравитационного поля Земли[3][4][5].
Сила тяжести сообщает всем телам, независимо от их массы, одно и то же ускорение[6] и является консервативной силой[7].
Сила тяжести P→{\displaystyle {\vec {P}}}, действующая на материальную точку массой m{\displaystyle m}, вычисляется по формуле[6]: P→=mg→{\displaystyle {\vec {P}}=m{\vec {g}}}, где g→{\displaystyle {\vec {g}}} – ускорение, сообщаемое телу силой тяжести, которое называется ускорением свободного падения
Если в пределах протяжённого тела поле сил тяжести однородно, то равнодействующая сил тяжести, действующих на элементы этого тела, приложена к центру масс тела[9].
На тела, движущиеся относительно поверхности Земли, кроме силы тяжести, также действует сила Кориолиса[10][11][12].
История
Аристотель объяснял силу тяжести движением тяжёлых физических стихий (земля, вода) к своему естественному месту (центру Вселенной внутри Земли), причём скорость тем больше, чем ближе тяжёлое тело к нему[13].
Архимед рассмотрел вопрос о центре тяжести параллелограмма, треугольника, трапеции и параболического сегмента. В сочинении «О плавающих телах» Архимед доказал закон гидростатики, носящий его имя[13].
Иордан Неморарий в сочинении «О тяжестях» при рассмотрении грузов на наклонной плоскости разлагал их силы тяжести на нормальную и параллельную наклонной плоскости составляющие, был близок к определению статического момента [14].
Стевин экспериментально определил, что тела разных масс падают с одинаковым ускорением, установил теоремы о давлении жидкости в сосудах (давление зависит только от глубины и не зависит от величины, формы и объёма сосуда) и о равновесии грузов на наклонной плоскости (на наклонных плоскостях равной высоты силы, действующие со стороны уравновешивающихся грузов вдоль наклонных плоскостей, обратно пропорциональны длинам этих плоскостей). Доказал теорему, согласно которой в случае равновесия центр тяжести однородного плавающего тела должен находиться выше центра тяжести вытесненной жидкости[15].
Галилей экспериментально исследовал законы падения тел (ускорение не зависит от веса тела), колебаний маятников (период колебаний не зависит от веса маятника) и движения по наклонной плоскости
Гюйгенс создал классическую теорию движения маятника, оказавшую значительное влияние на теорию тяготения[16].
Декарт разработал кинетическую теорию тяготения, объяснявшую силу тяжести взаимодействием тел с небесным флюидом, выдвинул гипотезу о зависимости силы тяжести от расстояния между тяжёлым телом и центром Земли[16].
Ньютон из равенства ускорений падающих тел и второго закона Ньютона сделал вывод о пропорциональности силы тяжести массам тел и установил, что сила тяжести является одним из проявлений силы всемирного тяготения[17][18].
Эйнштейн объяснил факт равенства ускорений падающих тел независимо от их массы (эквивалентность инертной и тяжёлой массы) как следствие принципа эквивалентности равномерно ускоренной системы отсчёта и системы отсчёта, находящейся в гравитационном поле[19].
Сферически симметричное тело
В соответствии с законом всемирного тяготения, сила гравитационного притяжения, действующая на материальную точку массой m{\displaystyle m} на поверхности сферически симметричного астрономического тела, имеющего массу M{\displaystyle M}, определяется соотношением:
- F=G⋅M⋅mR2,{\displaystyle F=G\cdot {M\cdot m \over R^{2}},}
где G{\displaystyle G} — гравитационная постоянная, равная 6,67384(80)·10−11м3·с−2·кг−1, а R{\displaystyle R} — радиус тела. Данное соотношение справедливо в предположении, что распределение массы по объёму тела сферически симметрично. В этом случае сила гравитационного притяжения направлена к центру тела.
Модуль центробежной силы инерции Q{\displaystyle Q}, действующей на материальную частицу, выражается формулой:
- Q=maω2,{\displaystyle Q=ma\omega ^{2},}
где a{\displaystyle a} — расстояние между частицей и осью вращения рассматриваемого астрономического тела, а ω{\displaystyle \omega } — угловая скорость его вращения. Центробежная сила инерции перпендикулярна оси вращения и направлена в сторону от неё.
Поправки, вносимые общей теорией относительности в закон всемирного тяготения Ньютона, в условиях Земли и других планет крайне малы (модуль гравитационного потенциала на поверхности Земли, равный половине квадрата второй космической скорости vII{\displaystyle v_{II}}, крайне мал по сравнению с квадратом скорости света c{\displaystyle c}: vII22c2∼10−10{\displaystyle {\frac {v_{II}^{2}}{2c^{2}}}\sim 10^{-10}})[20].
Земля
Форма Земли (геоид) отличается от шарообразной и близка к сплюснутому эллипсоиду. В этом случае сила гравитационного притяжения, действующая на материальную точку массой m{\displaystyle m}, определяется более сложным выражением, чем ранее:
F→=Gm∫MdMR2R→R.{\displaystyle {\vec {F}}=Gm\int \limits _{M}{{dM} \over {R^{2}}}{{\vec {R}} \over R}.}
Здесь dM{\displaystyle dM} — элемент массы Земли, R→=r→−r→′,{\displaystyle {\vec {R}}={\vec {r}}-{\vec {r}}’,} а r→{\displaystyle {\vec {r}}} и r→′{\displaystyle {{\vec {r}}’}} — радиус-векторы точки измерения и элемента Земли соответственно. Интегрирование при этом выполняется по всей массе Земли.
В векторной форме выражение для центробежной силы инерции можно записать в виде
- Q→=mω2R→0,{\displaystyle {\vec {Q}}=m\omega ^{2}{{\vec {R}}_{0}},}
где R→0{\displaystyle {{\vec {R}}_{0}}} — вектор, перпендикулярный оси вращения и проведённый от неё к данной материальной точке, находящейся вблизи поверхности Земли.
При этом сила тяжести P→{\displaystyle {\vec {P}}}, как и раньше, равна сумме F→{\displaystyle {\vec {F}}} и Q→{\displaystyle {\vec {Q}}}:
- P→=F→+Q→.{\displaystyle {\vec {P}}={\vec {F}}+{\vec {Q}}.}
Сила тяжести, действующая вблизи поверхности Земли, зависит от широты места φ{\displaystyle \varphi } и высоты его H{\displaystyle H} над уровнем моря. Приблизительное выражение для абсолютной величины силы тяжести в системе СИ имеет вид[8]:
- P=9,780318(1+0,005302sinφ−0,000006sin22φ)m−0,000003086Hm.{\displaystyle P=9,780318(1+0,005302\sin \varphi -0,000006\sin ^{2}2\varphi )m-0,000003086Hm.}
Угол α{\displaystyle \alpha } между силой тяжести P→{\displaystyle {\vec {P}}} и силой гравитационного притяжения к Земле F→{\displaystyle {\vec {F}}} равен[21]:
- α≈0,0018sin2φ{\displaystyle \alpha \approx 0,0018\sin {2\varphi }}.
Он изменяется в пределах от нуля (на экваторе, где φ=0∘{\displaystyle \varphi =0^{\circ }} и на полюсах, где φ=90∘{\displaystyle \varphi =90^{\circ }}) до 0,0018{\displaystyle 0,0018} рад или 6′{\displaystyle 6′} (на широте 45∘{\displaystyle 45^{\circ }}).
Движение тел под действием силы тяжести
В том случае, когда модуль перемещения тела много меньше расстояния до центра Земли, то можно считать силу тяжести постоянной, а движение тела равноускоренным. Если начальная скорость тела отлична от нуля и её вектор направлен не по вертикали, то под действием силы тяжести тело движется по параболической траектории.
При бросании тела с некоторой высоты параллельно поверхности Земли дальность полёта увеличивается с ростом начальной скорости. При больших значениях начальной скорости для вычисления траектории тела необходимо учитывать шарообразную форму Земли и изменение направления силы тяжести в разных точках траектории.
При некотором значении скорости, называемом первой космической скоростью, тело, брошенное по касательной к поверхности Земли, под действием силы тяжести при отсутствии сопротивления со стороны атмосферы может двигаться вокруг Земли по окружности, не падая на Землю. При скорости, превышающую вторую космическую скорость, тело уходит от поверхности Земли в бесконечность по гиперболической траектории. При скоростях, промежуточных между первой и второй космическими, тело движется вокруг Земли по эллиптической траектории[22].
Потенциальная энергия поднятого над Землей тела
Потенциальной энергией поднятого над Землей тела называется взятая с обратным знаком работа силы тяжести, совершаемая при перемещении тела с поверхности Земли в это положение. Она равна Ep=γMm(1Rz−1R){\displaystyle E_{p}=\gamma Mm({\frac {1}{R_{z}}}-{\frac {1}{R}})}, где γ{\displaystyle \gamma } – гравитационная постоянная, M{\displaystyle M} – масса земли, m{\displaystyle m} – масса тела, Rz{\displaystyle R_{z}} – радиус Земли, R{\displaystyle R} – расстояние до центра Земли тела.
При удалении тела не небольшие по сравнению с радиусом Земли расстояния от поверхности Земли поле тяготения можно считать однородным, то есть ускорение свободного падения постоянно. В этом случае при подъеме тела массой m{\displaystyle m} на высоту h{\displaystyle h} от поверхности Земли сила тяжести совершает работу A=−mgh{\displaystyle A=-mgh}. Поэтому потенциальная энергия тела: Ep=mgh{\displaystyle E_{p}=mgh}. Потенциальная энергия тела может иметь как положительные, так и отрицательные значения. Тело, находящееся на глубине h{\displaystyle h} от поверхности Земли обладает отрицательным значением потенциальной энергии Ep=−mgh{\displaystyle E_{p}=-mgh}[23].
При испарении воды с поверхности Земли солнечная радиация трансформируется в потенциальную энергию водяного пара в атмосфере. Затем при выпадении атмосферных осадков на сушу она переходит при стоке в кинетическую энергию и совершает эрозионную работу в процессе переноса денудационного материала всей суши и делает возможным жизнь органического мира на Земле[24].
Потенциальная энергия перемещаемых тектоническими процессами масс горных пород в основном тратится на перемещение продуктов разрушения горных пород с повышенных участков поверхности на нижерасположенные[25].
Значение в природе
Сила тяжести играет важную роль в процессах эволюции звёзд. Для звёзд, находящихся на этапе главной последовательности своей эволюции, сила тяжести является одним из важных факторов, обеспечивающих условия, необходимые для термоядерного синтеза. На заключительных этапах эволюции звёзд, в процессе их коллапса, благодаря силе тяжести, не скомпенсированной силами внутреннего давления, звёзды превращаются в нейтронные звёзды или чёрные дыры.
Сила тяжести очень важна для формирования структуры внутреннего строения Земли и других планет и тектонической эволюции её поверхности[26]. Чем больше сила тяжести, тем большая масса метеоритного материала выпадает на единицу её поверхности[27]. За время существования Земли её масса существенно увеличилась благодаря силе тяжести: ежегодно на Землю оседает 30-40 млн. тонн метеоритного вещества, в основном в виде пыли, что значительно превышает рассеяние лёгких компонентов верхней атмосферы Земли в космосе[28].
Без потенциальной энергии силы тяжести, непрерывно переходящей в кинетическую, круговорот вещества и энергии на Земле был бы невозможен[29].
Сила тяжести играет очень важную роль для жизни на Земле[30]. Только благодаря ей у Земли есть атмосфера. Вследствие силы тяжести, действующей на воздух, существует атмосферное давление[31].
У всех живых организмов с нервной системой есть рецепторы, определяющие величину и направление силы тяжести и служащие для ориентировки в пространстве. У позвоночных организмов, в том числе человека, величину и направление силы тяжести определяет вестибулярный аппарат[32].
Наличие силы тяжести привело к возникновению у всех многоклеточных наземных организмов прочных скелетов, необходимых для её преодоления. У водных живых организмов силу тяжести уравновешивает гидростатическая сила[33].
Роль силы тяжести в процессах жизнедеятельности организмов изучает гравитационная биология[34].
Применение в технике
Сила тяжести и принцип эквивалентности инертной и гравитационной массы используются для определения масс предметов путём их взвешивания на весах. Сила тяжести используется при отстойной сепарации газовых и жидких смесей, в некоторых типах часов, в отвесах и противовесах, машине Атвуда и жидкостных барометрах.
Точные измерения силы тяжести и её градиента (гравиметрия) используются при исследовании внутреннего строения Земли и при гравиразведке различных полезных ископаемых[35].
Устойчивость тела в поле силы тяжести
Для тела в поле силы тяжести, опирающегося на одну точку (например при подвешивании тела за одну точку или помещении шара на плоскость) для устойчивого равновесия необходимо, что бы центр тяжести тела занимал наинизшее положение по сравнению со всеми возможными соседними положениями[36].
Для тела в поле силы тяжести, опирающегося на несколько точек (например, стол) или на целую площадку (например, ящик на горизонтальной плоскости) для устойчивого равновесия необходимо, чтобы вертикаль, проведённая через центр тяжести, проходила внутри площади опоры тела. Площадью опоры тела называется контур, соединяющий точки опоры или внутри площадки, на которое опирается тело[36].
Методы измерения силы тяжести
- Основной источник: [37]
Силу тяжести измеряют динамическими и статическими методами. Динамические методы используют наблюдение за движением тела под действием силы тяжести и измеряют время перехода тела из одного заранее определённого положения в другое. Они используют: колебания маятника, свободное падение тела, колебания струны с грузом. Статические методы используют наблюдение за изменением положения равновесия тела под действием силы тяжести и некоторой уравновешивающей её силы и измеряют линейное или угловое смещение тела.
Измерения силы тяжести бывают абсолютными и относительными. Абсолютные измерения определяют полное значение силы тяжести в заданной точке. Относительные измерения определяют разность силы тяжести в заданной точке и некоторого другого, заранее известного значения. Приборы, предназначенные для относительных измерений силы тяжести, называются гравиметрами.
Динамические методы определения силы тяжести могут быть как относительными, так и абсолютными, статические – только относительными.
Сила тяжести на других планетах
| Земля | 1,00 | Солнце | 27,85 |
| Луна | 0,165 | Меркурий | 0,375—0,381 |
| Венера | 0,906 | Марс | 0,394 |
| Юпитер | 2,442 | Сатурн | 1,065 |
| Уран | 0,903 | Нептун | 1,131 |
См. также
Примечания
- ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 372. — 560 с. — ISBN 5-9221-0225-7.
- ↑ Тарг С. М. Сила тяжести // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 496. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Миронов, 1980, с. 49.
- ↑ Максимальное изменение силы тяжести, обусловленное притяжением Луны, составляет примерно 0,25∗10−5{\displaystyle 0,25*10^{-5}} м/с2, Солнца 0,1∗10−5{\displaystyle 0,1*10^{-5}} м/с2
- ↑ Миронов, 1980, с. 71.
- ↑ 1 2 Савельев, 1987, с. 70.
- ↑ Савельев, 1987, с. 82-83.
- ↑ 1 2 Ускорение свободного падения // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — Т. 5. — С. 245—246. — 760 с. — ISBN 5-85270-101-7.
- ↑ Савельев, 1987, с. 156.
- ↑ Тарасов, 2012, с. 200, 270.
- ↑ Савельев, 1987, с. 128.
- ↑ Бутенин, 1971, с. 253-259.
- ↑ 1 2 Зубов В. П. Физические идеи древности // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 38, 54-55;
- ↑ Зубов В. П. Физические идеи средневековья // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 114;
- ↑ Зубов В. П. Физические идеи ренессанса // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 151;
- ↑ 1 2 3 Кузнецов Б. Г. Генезис механического объяснения физических явлений и идеи картезианской физики // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 160-161, 169-170, 177;
- ↑ Ньютон, 1989, с. 7.
- ↑ Кузнецов Б. Г. Основные принципы физики Ньютона // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 189-191;
- ↑ Иваненко Д. Д. Основные идеи общей теории относительности // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 300;
- ↑ Грищук Л. П., Зельдович Я. Б. Тяготение // Физика космоса. Маленькая энциклопедия. — М., Советская энцилопедия, 1986. — С. 676
- ↑ Савельев, 1987, с. 122.
- ↑ Жирнов Н. И. Классическая механика. — М., Просвещение, 1980. — Тираж 28000 экз. – с. 121
- ↑ Кабардин О.Ф., Орлов В.А., Пономарева А.В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985. — Тираж 143 500 экз. — С. 151 – 152
- ↑ Криволуцкий, 1985, с. 307.
- ↑ Криволуцкий, 1985, с. 70, 234.
- ↑ Криволуцкий, 1985, с. 208.
- ↑ Криволуцкий, 1985, с. 77.
- ↑ Криволуцкий, 1985, с. 48, 237-238.
- ↑ Криволуцкий, 1985, с. 289.
- ↑ Зельманов А. Л. Многообразие материального мира и проблема бесконечности Вселенной // Бесконечность и Вселенная. — М., Мысль, 1969. — Тираж 12000 экз. – С. 283
- ↑ Хромов С. П., Петросянц М. А. Метеорология и климатология. – М., МГУ, 2006. – ISBN 5-211-05207-2. – C. 67
- ↑ Юрий Фролов. https://www.nkj.ru/archive/articles/21172/ Наш гравитационный компас] // Наука и жизнь. — 2012. — № 10.
- ↑ П. Кемп, К. Армс Введение в биологию. — М.: Мир, 1988. — ISBN 5-03-001286-9. — Тираж 125000 экз. — С. 75
- ↑ Лозовская Е. Жизнь с гравитацией и без нее // Наука и жизнь. — 2004. — № 9.
- ↑ Миронов, 1980, с. 1-543.
- ↑ 1 2 Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика, теплота, молекулярная физика. — М., Наука, 1975. — Тираж 350 000 экз. — С. 189-190
- ↑ Миронов, 1980, с. 94-262.
- ↑ У газовых гигантов «поверхность» понимается как область высот в атмосфере, где давление равно атмосферному давлению на Земле на уровне моря (1,013×105Па).
- ↑ Данные взяты из статьи Википедии Ускорение свободного падения
Литература
- Ньютон И. Математические начала натуральной философии. — М.: Наука, 1989. — 688 с. — ISBN 5-02-000747-1.
- Савельев И. В. Курс общей физики. Т. 1. Механика. Молекулярная физика. — М.: Наука, 1987. — 688 с.
- Криволуцкий А. Е. Голубая планета. Земля среди планет. Географический аспект.. — М.: Мысль, 1985. — 335 с.
- Миронов В. С. Курс гравиразведки. — Л.: Недра, 1980. — 543 с.
- Тарасов В. Н., Бояркина И. В., Коваленко М. В., Федорченко Н. П., Фисенко Н. И. Теоретическая механика. — М.: ТрансЛит, 2012. — 560 с.
- Бутенин Н. В. Введение в аналитическую механику. — М.: Наука, 1971. — 264 с. — 25 000 экз.
wikiredia.ru
Что такое сила притяжения
Когда на уроках физики в начальных классах преподаватель упоминает существовавшее ранее представление о планете Земле как о плоскости, покоящейся на китах, слонах или черепахах, то на лицах учеников появляются улыбки и в классе даже раздаются смешки. Это сейчас многие уже в детском садике знают, что Земля – это шар, а сила притяжения воздействует на все материальные предметы. Однако давайте хотя бы на мгновение представим, что о гравитации нам ничего не известно. Как тогда объяснить, что люди удерживаются на поверхности, а вода океанов не изливается в пустоту космического пространства, если не воспользоваться представлением о плоской планете? Если сила притяжения для нас тайна – то, пожалуй, никак. Именно поэтому так важно относится с пониманием к прошлому, ведь каждому времени – свои открытия.
Сила гравитационного притяжения была открыта И. Ньютоном в 1666 году. До него тяготение пытались объяснить такие выдающиеся ученые своего времени, как Гюйгенс, известный своими трудами по центробежной силе, Декарт, а также Кеплер, сформулировавший фундаментальные три закона, которым подчиняется перемещение небесных объектов. Однако это были лишь предположения, основывающиеся скорее на догадках, а не на фактах. Ни одно из них не давало целостного понимания мироустройства. Ньютон же намеревался создать завершенную теорию, в рамках которой могла быть объяснена сила притяжения и взаимосвязанные с ней явления. И это ему удалось. Были сформулированы не просто теоретические предпосылки с формулами, а создана полноценная модель. Она оказалась настолько удачной, что даже сейчас, спустя столетия, общая теория относительности, будучи развитием идей Ньютона, используется при расчетах небесной механики.
Ее формулировка крайне простая и запоминающаяся: сила, с которой объекты притягиваются, зависит от их массы и расстояния. Данное определение выражается следующим образом:
F = (M1*M2) / (R*R),
где M1 и M2 – массы объектов; R – расстояние.
Обычно знакомство с классической теорией начинают именно с этой формулы. Для более точного представления всю правую часть следует умножить на гравитационную константу.
Вывод следующий: чем объект массивнее, тем более сильное притягивающее воздействие он оказывает на окружение. При этом совершенно не принципиально, будет ли это сфера массой 1 кг, или точка с таким же весом. В то же время, при расчете системы двух тел, например, Солнца и Земли, последняя точно так же притягивает звезду к себе. Сила притяжения земли, взаимодействующая с полем Солнца, формирует общий центр масс, вокруг которого происходит взаимное обращение. Это только кажется, что Солнце – центр нашей системы. Истинный же, хотя и находится в звезде, с физической серединной точкой не совпадает.
Сила притяжения может быть определена в рамках классического закона всемирного тяготения при соблюдении двух условий:
– скорости объектов рассматриваемой системы значительно меньше скорости луча света;
– потенциал гравитационного поля относительно мал.
В скором времени после завершения Ньютоном работ по притяжению, стала очевидной необходимость ее существенной доработки. Дело в том, что хотя движение тел небесной сферы можно было рассчитывать с помощью предложенных формул, иногда возникали ситуации, когда теория Ньютона оказывалась неприменимой, так как давала совершенно непредсказуемые результаты.
Недостатки были устранены Эйнштейном, предложившим серьезно доработанную модель, учитывающую как скорость света, так и слишком сильные гравитационные поля. Однако сейчас даже такая общая теория относительности перестала быть универсальным ответом на все вопросы: в микромире ее постулаты оказываются неверны.
autogear.ru
Что такое сила притяжения? Почему два тела притягиваются друг к другу?
природа силы тяготения не раскрыта. экспериментально наблюдаемый факт, что тела притягиваются к друг другу. дальше почесали затылок и договорились (ученые) , что любые два тела обладающие массой притягиваются. т. е. сейчас понимается, что масса и сила тяготения неразрывно связаны.
сила притяжения равна разности магнитных полей этих людей! ! Еще магические способности нашего мозга – очень малораскрыты!!
Что такое сила притяжения – не знаю. А насчет ТЕЛ – все просто.
ТЯГОТЕНИЕ (ГРАВИТАЦИЯ) , свойство материи, которое состоит в том, что между любыми двумя частицами существуют силы притяжения. Тяготение — универсальное взаимодействие, охватывающее всю доступную наблюдению Вселенную и потому называемое всемирным. .. <a rel=”nofollow” href=”http://slovari.yandex.ru/dict/krugosvet/article/a/a1/1002291.htm?text” target=”_blank”>http://slovari.yandex.ru/dict/krugosvet/article/a/a1/1002291.htm?text</a>=
Если отвечать не шаблонно, то что такое притяжение (гравитация) никто не знает. Это просто установленный факт. Есть различные теории, гипотезы, но они остаются пока только теориями и гипотезами
u odnovo + u drugova -,a oni ne mogut drug bez druga,ili on ogoni ona voda,bez nih net smisla,ili vozduh s dniom,..
потому что между ними существует гравитационное поле, его напряжённость пропорциональна массе тела.
touch.otvet.mail.ru



