Температура газа формула – Молекулярная физика. Основные положения МКТ. Основные понятия и формулы. Свойства идеального газа. Основное уравнение МКТ. Температура. Уравнение состояния идеального газа. Уравнение Менделеева-Клайперона. Газовые законы – изотерма, изобара, изохора
- Комментариев к записи Температура газа формула – Молекулярная физика. Основные положения МКТ. Основные понятия и формулы. Свойства идеального газа. Основное уравнение МКТ. Температура. Уравнение состояния идеального газа. Уравнение Менделеева-Клайперона. Газовые законы – изотерма, изобара, изохора нет
- Советы абитуриенту
- Абсолютная температура идеального газа
- Основное уравнение МКТ газов. Температура – HomeWork.net.ua
- Основное уравнение МКТ газов. Температура
- Основное уравнение МКТ газов. Температура
- 2.1.2 Идеальный газ. Давление и температура газа. Шкала температур
- Связь между давлением, температурой, объемом и количеством молей газа (“массой” газа). Универсальная (молярная) газовая постоянная R. Уравнение Клайперона-Менделеева = уравнение состояния идеального газа.
- АБСОЛЮТНАЯ ТЕМПЕРАТУРА ГАЗА: Смотреть что такое “АБСОЛЮТНАЯ ТЕМПЕРАТУРА” в других словарях:
Абсолютная температура идеального газа
Давление газа определяют хаотические удары перемещающихся молекул. Это означает, что уменьшение давления при охлаждении газа можно объяснить уменьшением средней энергии поступательного движения молекул (). Давление газа достигнет нуля, когда в соответствии с основным законом молекулярно кинетической теории:
. Концентрация молекул газа n считается постоянной отличной от нуля.
Абсолютная температура идеального газа
Для охлаждения газа существует предел. Абсолютным нулем называют температуру, при которой прекращается поступательное движение молекул.
Идеальный газ (в отличие от реальных газов) остается в газообразном состоянии при любых температурах. Величину температуры, при которой прекратится поступательное движение молекул, можно найти из закона, который определил Ж. Шарль: температурный коэффициент давления идеального газа не зависит от рода газа и равен . При этом давление идеального газа при произвольной температуре равно:
где t – температура по шкале Цельсия; – давление при . Приравняем давление в выражении (2) к нулю, выразим температуру, при которой молекулы идеального газа прекратят свое поступательное движение:
В. Кельвин предположил, что полученное значение абсолютного нуля будет соответствовать прекращению поступательного движения молекул любого вещества. Температуры ниже абсолютного нуля (T=0 К) природе не бывает. Так как при температуре абсолютного нуля нельзя отнимать энергию теплового движения молекул и уменьшать температуру тела, так как энергия теплового движения отрицательной быть не может. В лабораториях получена температура близкая к абсолютному нулю (около тысячной доли градуса).
Термодинамическая шкала температур
По термодинамической шкале температур (она же шкала Кельвина) началом отсчета считается абсолютный нуль температур. Температуру обозначают большой буквой T. Размер градуса совпадает с градусом по шкале Цельсия:
Одинаковыми будут производные, если брать их с использованием разных температурных кал:
При переходе от шкалы Кельвина к шкале Цельсия сохраняются определения термических коэффициентов объемного расширения и коэффициента давления.
В международной системе единиц (СИ) единица температуры является основной, ее называют кельвином (К). В системе СИ термодинамическая шкала температур используется для отсчета температуры.
В соответствии с международным соглашением размер кельвина определяют из таких условий: температуру тройной точки волы принимают равной 273,16 К. Тройной точке воды по Цельсию, соответствует 0,01 oС, температура таяния льда по кельвину равна 273,15 К.
Температура, измеряемая в кельвинах, называется абсолютной. Связью между абсолютной температурой и температурой по Цельсию отражает выражение:
Абсолютная температура, кинетическая энергия молекул и давление идеального газа
Величина средней энергии поступательного движения молекул прямо пропорциональна температуре газа:
где – постоянная Больцмана. Формула (6) означает, что средняя величина кинетической энергии поступательного движения молекул не зависит от рода идеального газа, а определено только его температурой.
Давление идеального газа определено только его температурой:
Примеры решения задач
ru.solverbook.com
Основное уравнение МКТ газов. Температура – HomeWork.net.ua
Простейшей моделью молекулярно-кинетической теории является модель безупречного газа. В кинетической модели безупречного газа молекулы рассматриваются как совершенно упругие шарики, взаимодействующие меж собой и со стенами только во время упругих столкновений. Суммарный объем всех молекул подразумевается малым по сопоставлению с объемом сосуда, в каком находится газ. Модель безупречного газа довольно отлично обрисовывает поведение реальных газов в широком спектре давлений и температур.
Задачка молекулярно-кинетической теории заключается в том, чтоб установить связь меж микроскопичными (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, газ, температура). В итоге каждого столкновения меж молекулами и молекул со стеной скорости молекул могут изменяться по модулю и по направлению; на интервалах меж поочередными столкновениями молекулы движутся умеренно и прямолинейно.
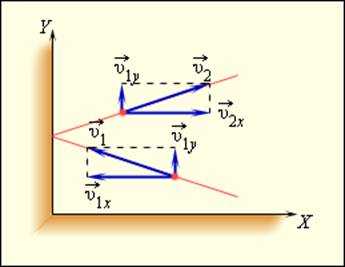
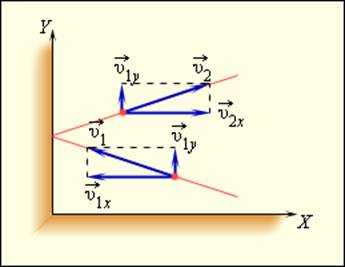
В модели безупречного газа подразумевается, что все столкновения происходят по законам упругого удара, другими словами подчиняются законам механики Ньютона. Используя модель безупречного газа, вычислим давление газа на стену сосуда. В процессе взаимодействия молекулы со стеной сосуда меж ними появляются силы, подчиняющиеся третьему закону Ньютона. В итоге проекция υx скорости молекулы, перпендикулярная стене, изменяет собственный символ на обратный, а проекция υy скорости, параллельная стене, остается постоянной (рис. 3.2.1).
 1 1 |
| Набросок 3.2.1. Упругое столкновение молекулы со стеной. |
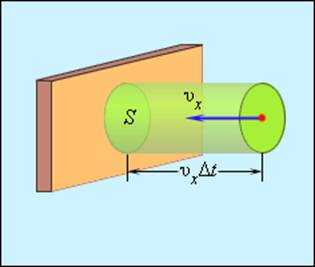
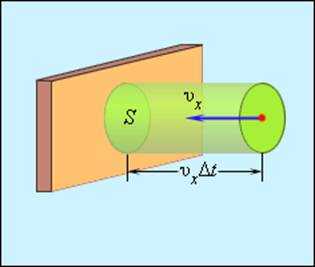
Потому изменение импульса молекулы будет равно 2m0υx, где m0 – масса молекулы. Выделим на стене некую площадку S (рис. 3.2.2). За время Δt с этой площадкой столкнутся все молекулы, имеющие проекцию скорости υx, направленную в сторону стены, и находящиеся в цилиндре с основанием площади S и высотой υxΔt.
 2 2 |
| Набросок 3.2.2. Определение числа столкновений молекул с площадкой S. |
Пусть в единице объема сосуда содержатся n молекул; тогда число молекул в объеме цилиндра равно nSυxΔt. Но из этого числа только половина движется в сторону стены, а другая половина движется в обратном направлении и со стеной не сталкивается. Как следует, число ударов молекул о площадку S за время Δt равно Так как любая молекула при столкновении со стеной изменяет собственный импульс на величину 2m0υx, то полное изменение импульса всех молекул, столкнувшихся за время Δt с площадкой S, равно По законам механики это изменение импульса всех столкнувшихся со стеной молекул происходит под действием импульса силы FΔt, где F – некая средняя сила, действующая на молекулы со стороны стены на площадке S. Но по 3-му закону Ньютона такая же по модулю сила действует со стороны молекул на площадку S. Потому можно записать:
Разделив обе части на SΔt, получим:
где p – давление газа на стену сосуда. При выводе этого соотношения предполагалось, что все n молекул, содержащихся в единице объема газа, имеют однообразные проекции скоростей на ось X. По сути это не так. В итоге бессчетных соударений молекул газа меж собой и со стенами в сосуде, содержащем огромное число молекул, устанавливается некое статистическое рассредотачивание молекул по скоростям. При всем этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а модули скоростей и их проекции на координатные оси подчиняются определенным закономерностям.
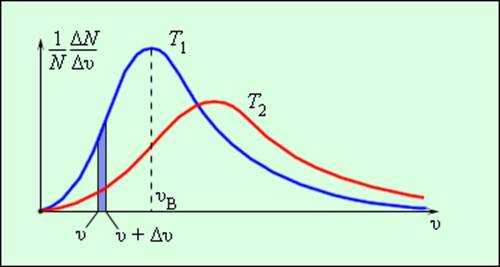
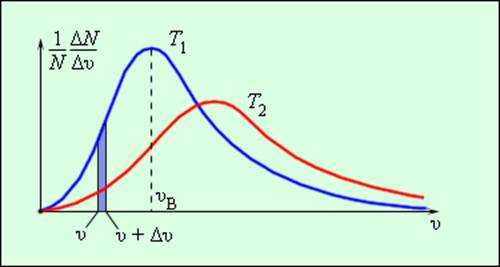
Рассредотачивание молекул газа по модулю скоростей именуется рассредотачиванием Максвелла (1860 г.). Дж. Максвелл ввел закон рассредотачивания молекул газа по скоростям, исходя из главных положений молекулярно-кинетической теории. На рис. 3.2.3 представлены обычные кривые рассредотачивания молекул по скоростям. По оси абсцисс отложен модуль скорости, а по оси ординат – относительное число молекул, скорости которых лежат в интервале от υ до υ + Δυ. Это число равно площади выделенного на рис. 3.2.3 столбика.
 3 3 |
| Набросок 3.2.3. Рассредотачивание молекул по скоростям. T2 > T1. |
Соответствующими параметрами рассредотачивания Максвелла являются более возможная скорость υв, соответственная максимуму кривой рассредотачивания, и среднеквадратичная скорость где – среднее значение квадрата скорости. С ростом температуры максимум кривой рассредотачивания сдвигается в сторону огромных скоростей, при всем этом υв и υкв растут. Чтоб уточнить формулу для давления газа на стену сосуда, представим, что все молекулы, находящиеся в единице объема, разбиты на группы, содержащие n1, n2, n3 и т. д. молекул с проекциями скоростей υx1, υx2, υx3 и т. д. соответственно. При всем этом Любая группа молекул заносит собственный вклад в давление газа. В итоге соударений со стеной молекул с разными значениями проекций υxi скоростей появляется суммарное давление
Входящая в это выражение сумма – это сумма квадратов проекций υx всех n молекул в единичном объеме газа. Если эту сумму поделить на n, то мы получим среднее значение квадрата проекции скорости молекул:
Сейчас формулу для давления газа можно записать в виде
Потому что все направления для векторов скоростей молекул равновероятны, среднее значение квадратов их проекций на координатные оси равны меж собой:
Последнее равенство вытекает из формулы: Формула для среднего давления газа на стену сосуда запишется в виде
Это уравнение устанавливает связь меж давлением p безупречного газа, массой молекулы m0, концентрацией молекул n, средним значением квадрата скорости и средней кинетической энергией поступательного движения молекул. Его именуют главным уравнением молекулярно-кинетической теории газов. Таким макаром, давление газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема. В основное уравнение молекулярно-кинетической теории газов заходит произведение концентрации молекул n на среднюю кинетическую энергию поступательного движения. Если представить, что газ находится в сосуде постоянного объема V, то (N – число молекул в сосуде). В данном случае изменение давления Δp пропорционально изменению средней кинетической энергии. Появляются вопросы: каким образом можно на опыте изменять среднюю кинетическую энергию движения молекул в сосуде постоянного объема? Какую физическую величину необходимо поменять, чтоб поменялась средняя кинетическая энергия Таковой величиной в физике является
Для измерения температуры употребляются физические приборы – указатели температуры, в каких о величине температуры судят по изменению какого-нибудь физического параметра. Для сотворения указателя температуры нужно избрать термометрическое вещество (к примеру, ртуть, спирт) и термометрическую величину, характеризующую свойство вещества (к примеру, длина ртутного либо спиртового столбика). В разных конструкциях термометров употребляются различные физические характеристики вещества (к примеру, изменение линейных размеров жестких тел либо изменение электронного сопротивления проводников при нагревании).
Указатели температуры должны быть откалиброваны. Для этого их приводят в термический контакт с телами, температуры которых числятся данными. В большинстве случаев употребляют обыкновенные природные системы, в каких температура остается постоянной, невзирая на термообмен с окружающей средой – это смесь льда и воды и смесь воды и пара при кипении при обычном атмосферном давлении. По температурной шкале Цельсия точке плавления льда приписывается температура 0 °С, а точке кипения воды – 100 °С. Изменение длины столба воды в капиллярах указателя температуры на одну сотую длины меж отметками 0 °С и 100 °С принимается равным 1 °С. В ряде государств (США) обширно употребляется шкала Фаренгейта (TF), в какой температура замерзающей воды принимается равной 32 °F, а температура кипения воды равной 212 °F. Как следует,
Особенное место в физике занимают газовые указатели температуры (рис. 3.2.4), в каких термометрическим веществом является разреженный газ (гелий, воздух) в сосуде постоянного объема (V = const), а термометрической величиной – давление газа p. Опыт указывает, что давление газа (при V = const) вырастает с ростом температуры, измеренной по шкале Цельсия.
 4 4 |
| Набросок 3.2.4. Газовый указатель температуры с неизменным объемом. |
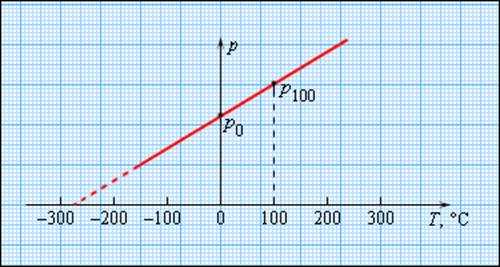
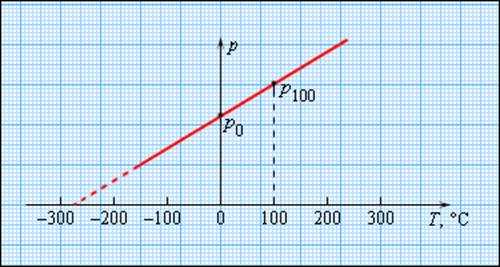
Чтоб проградуировать газовый указатель температуры неизменного объема, можно измерить давление при 2-ух значениях температуры (к примеру, 0 °C и 100 °C), нанести точки p0 и p100 на график, а потом провести меж ними прямую линию (рис. 3.2.5). Используя приобретенный таким макаром калибровочный график, можно определять температуры, надлежащие другим значениям давления. Экстраполируя график в область низких давлений, можно найти некую «гипотетичную» температуру, при которой давление газа стало бы равным нулю. Опыт указывает, что эта температура равна –273,15 °С и не находится в зависимости от параметров газа. Нереально на опыте получить методом остывания газ в состоянии с нулевым давлением, потому что при очень низких температурах все газы перебегают в водянистые либо твердые состояния.
| 5 |
| Набросок 3.2.5. Зависимость давления газа от температуры при V = const. |
Британский физик У. Кельвин (Томсон) в 1848 г. предложил использовать точку нулевого давления газа для построения новейшей температурной шкалы (шкала Кельвина). В этой шкале единица измерения температуры такая же, как и в шкале Цельсия, но нулевая точка сдвинута:
В системе СИ принято единицу измерения температуры по шкале Кельвина именовать кельвином и обозначать буковкой К. К примеру, комнатная температура TС = 20 °С по шкале Кельвина равна TК = 293,15 К. Температурная шкала Кельвина именуется абсолютной шкалой температур. Она оказывается более комфортной при построении физических теорий. Нет необходимости привязывать шкалу Кельвина к двум фиксированным точкам – точке плавления льда и точке кипения воды при обычном атмосферном давлении, как это принято в шкале Цельсия. Не считая точки нулевого давления газа, которая именуется абсолютным нулем температуры, довольно принять еще одну фиксированную опорную точку.
В шкале Кельвина в качестве таковой точки употребляется температура тройной точки воды (0,01 °С), в какой в термическом равновесии находятся все три фазы – лед, вода и пар. По шкале Кельвина температура тройной точки принимается равной 273,16 К. Газовые указатели температуры громоздки и неудобны для практического внедрения: они употребляются в качестве прецизионного эталона для калибровки других термометров. Таким макаром, давление разреженного газа в сосуде неизменного объема V меняется прямо пропорционально его абсолютной температуре: p ~ T. С другой стороны, опыт указывает, что при постоянных объеме V и температуре T давление газа меняется прямо пропорционально отношению количества вещества ν в данном сосуде к объему V сосуда
где N – число молекул в сосуде, NА – неизменная Авогадро, n = N / V – концентрация молекул (другими словами число молекул в единице объема сосуда). Объединяя эти соотношения пропорциональности, можно записать:
где k – некая универсальная для всех газов неизменная величина. Ее именуют неизменной Больцмана, в честь австрийского физика Л. Больцмана (1844–1906 гг.), 1-го из создателей молекулярно-кинетической теории. Неизменная Больцмана – одна из базовых физических констант. Ее численное значение в СИ равно:
| k = 1,38·10–23 Дж/К. |
Сравнивая соотношения p = nkT с главным уравнением молекулярно-кинетической теории газов, можно получить:
Средняя кинетическая энергия хаотического движения молекул газа прямо пропорциональна абсолютной температуре. Таким макаром, температура есть мера средней кинетической энергии поступательного движения молекул. Следует направить внимание на то, что средняя кинетическая энергия поступательного движения молекулы не находится в зависимости от ее массы. Броуновская частичка, взвешенная в воды либо газе, обладает таковой же средней кинетической энергией, как и отдельная молекула, масса которой на много порядков меньше массы броуновской частички. Этот вывод распространяется и на случай, когда в сосуде находится смесь химически невзаимодействующих газов, молекулы которых имеют различные массы. В состоянии равновесия молекулы различных газов будут иметь однообразные средние кинетические энергии термического движения, определяемые только температурой консистенции. Давление консистенции газов на стены сосуда будет складываться из парциальных давлений каждого газа:
|
В этом соотношении n1, n2, n3, … – концентрации молекул разных газов в консистенции. Это соотношение выражает на языке молекулярно-кинетической теории экспериментально установленный сначала XIX столетия закон Дальтона: давление в консистенции химически невзаимодействующих газов равно сумме их парциальных давлений.
homework.net.ua
Основное уравнение МКТ газов. Температура
Простейшей моделью, рассматриваемой молекулярно-кинетической теорией, является модель идеального газа. В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур. Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, объем, температура).
В результате каждого столкновения между молекулами и молекул со стенками скорости молекул могут изменяться по модулю и по направлению; на интервалах времени между последовательными столкновениями молекулы движутся равномерно и прямолинейно. В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т. е. подчиняются законам механики Ньютона.
Используя модель идеального газа, вычислим давление газа на стенку сосуда. В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υy скорости, параллельная стенке, остается неизменной (рис. 3.2.1).
|
Рисунок 3.2.1. Упругое столкновение молекулы со стенкой |
Поэтому изменение импульса молекулы будет равно 2m0υx, где m0 – масса молекулы.
Выделим на стенке некоторую площадку S (рис. 3.2.2). За время Δt с этой площадкой столкнутся все молекулы, имеющие проекцию скорости υx, направленную в сторону стенки, и находящиеся в цилиндре с основанием площади S и высотой υxΔt.
|
Рисунок 3.2.2. Определение числа столкновений молекул с площадкой S |
Пусть в единице объема сосуда содержатся n молекул; тогда число молекул в объеме цилиндра равно nSυxΔt. Но из этого числа лишь половина движется в сторону стенки, а другая половина движется в противоположном направлении и со стенкой не сталкивается. Следовательно, число ударов молекул о площадку S за время Δt равно
Поскольку каждая молекула при столкновении со стенкой изменяет свой импульс на величину 2m0υx, то полное изменение импульса всех молекул, столкнувшихся за время Δt с площадкой S, равно
По законам механики это изменение импульса всех столкнувшихся со стенкой молекул происходит под действием импульса силы FΔt, где F – некоторая средняя сила, действующая на молекулы со стороны стенки на площадке S. Но по 3-му закону Ньютона такая же по модулю сила действует со стороны молекул на площадку S. Поэтому можно записать:
Разделив обе части на SΔt, получим:
где p – давление газа на стенку сосуда.
При выводе этого соотношения предполагалось, что все n молекул, содержащихся в единице объема газа, имеют одинаковые проекции скоростей на ось X. На самом деле это не так.
В результате многочисленных соударений молекул газа между собой и со стенками в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а модули скоростей и их проекции на координатные оси подчиняются определенным закономерностям. Распределение молекул газа по модулю скоростей называется распределением Максвелла. Джеймс Максвелл в 1860 г. вывел закон распределения молекул газа по скоростям, исходя из основных положений молекулярно-кинетической теории. На рис. 3.2.3 представлены типичные кривые распределения молекул по скоростям. По оси абсцисс отложен модуль скорости, а по оси ординат – относительное число молекул, скорости которых лежат в интервале от υ до υ + Δυ. Это число равно площади выделенного на рис. 3.2.3 столбика.
|
Рисунок 3.2.3. Распределение молекул по скоростям. T2 > T1 |
Характерными параметрами распределения Максвелла являются наиболее вероятная скорость υв, соответствующая максимуму кривой распределения, и среднеквадратичная скорость
где
– среднее значение квадрата скорости.
С ростом температуры максимум кривой распределения смещается в сторону больших скоростей, при этом υв и υкв увеличиваются.
Чтобы уточнить формулу для давления газа на стенку сосуда, предположим, что все молекулы, содержащиеся в единице объема, разбиты на группы, содержащие n1, n2, n3 и т. д. молекул с проекциями скоростей υx1, υx2, υx3 и т. д. соответственно. При этом
Каждая группа молекул вносит свой вклад
в давление газа. В результате соударений со стенкой молекул с различными значениями проекций υxi скоростей возникает суммарное давление
Входящая в это выражение сумма – это сумма квадратов проекций υx всех n молекул в единичном объеме газа. Если эту сумму разделить на n, то мы получим среднее значение квадрата проекции скорости молекул:
Теперь формулу для давления газа можно записать в виде
Так как все направления для векторов скоростей молекул равновероятны, среднее значение квадратов их проекций на координатные оси равны между собой:
Последнее равенство вытекает из формулы:
Формула для среднего давления газа на стенку сосуда запишется в виде
Это уравнение устанавливает связь между давлением p идеального газа, массой молекулы m0, концентрацией молекул n, средним значением квадрата скорости и средней кинетической энергией поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов.
Таким образом, давление газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.
В основное уравнение молекулярно-кинетической теории газов входит произведение концентрации молекул n на среднюю кинетическую энергию поступательного движения. Если предположить, что газ находится в сосуде неизменного объема V, то
(N – число молекул в сосуде). В этом случае изменение давления Δp пропорционально изменению средней кинетической энергии.
Возникают вопросы: каким образом можно на опыте изменять среднюю кинетическую энергию движения молекул в сосуде неизменного объема? Какую физическую величину нужно изменить, чтобы изменилась средняя кинетическая энергия Опыт показывает, что такой величиной является температура.
Понятие температуры тесно связано с понятием теплового равновесия. Тела, находящиеся в контакте друг с другом, могут обмениваться энергией. Энергия, передаваемая одним телом другому при тепловом контакте, называется количеством теплоты.
Тепловое равновесие – это такое состояние системы тел, находящихся в тепловом контакте, при котором не происходит теплопередачи от одного тела к другому, и все макроскопические параметры тел остаются неизменными. Температура – это физический параметр, одинаковый для всех тел, находящихся в тепловом равновесии. Возможность введения понятия температуры следует из опыта и носит название нулевого закона термодинамики.
Для измерения температуры используются физические приборы – термометры, в которых о величине температуры судят по изменению какого-либо физического параметра. Для создания термометра необходимо выбрать термометрическое вещество (например, ртуть, спирт) и термометрическую величину, характеризующую свойство вещества (например, длина ртутного или спиртового столбика). В различных конструкциях термометров используются разнообразные физические свойства вещества (например, изменение линейных размеров твердых тел или изменение электрического сопротивления проводников при нагревании).
Термометры должны быть откалиброваны. Для этого их приводят в тепловой контакт с телами, температуры которых считаются заданными. Чаще всего используют простые природные системы, в которых температура остается неизменной, несмотря на теплообмен с окружающей средой – это смесь льда и воды и смесь воды и пара при кипении при нормальном атмосферном давлении. По температурной шкале Цельсия точке плавления льда приписывается температура 0 °С, а точке кипения воды – 100 °С. Изменение длины столба жидкости в капиллярах термометра на одну сотую длины между отметками 0 °С и 100 °С принимается равным 1 °С. В ряде стран (США) широко используется шкала Фаренгейта (TF), в которой температура замерзающей воды принимается равной 32 °F, а температура кипения воды равной 212 °F. Следовательно,
Особое место в физике занимают газовые термометры (рис. 3.2.4), в которых термометрическим веществом является разреженный газ (гелий, воздух) в сосуде неизменного объема (V = const), а термометрической величиной – давление газа p. Опыт показывает, что давление газа (при V = const) растет с ростом температуры, измеренной по шкале Цельсия.
|
Рисунок 3.2.4. Газовый термометр с постоянным объемом |
Чтобы проградуировать газовый термометр постоянного объема, можно измерить давление при двух значениях температуры (например, 0 °C и 100 °C), нанести точки p0 и p100 на график, а затем провести между ними прямую линию (рис. 3.2.5). Используя полученный таким образом калибровочный график, можно определять температуры, соответствующие другим значениям давления. Экстраполируя график в область низких давлений, можно определить некоторую «гипотетическую» температуру, при которой давление газа стало бы равным нулю. Опыт показывает, что эта температура равна –273,15 °С и не зависит от свойств газа. На опыте получить путем охлаждения газ в состоянии с нулевым давлением невозможно, так как при очень низких температурах все газы переходят в жидкое или твердое состояние.
|
Рисунок 3.2.5. Зависимость давления газа от температуры при V = const |
Английский физик У. Кельвин (Томсон) в 1848 г. предложил использовать точку нулевого давления газа для построения новой температурной шкалы (шкала Кельвина). В этой шкале единица измерения температуры такая же, как и в шкале Цельсия, но нулевая точка сдвинута:
В системе СИ принято единицу измерения температуры по шкале Кельвина называть кельвином и обозначать буквой K. Например, комнатная температура TС = 20 °С по шкале Кельвина равна TК = 293,15 К.
Температурная шкала Кельвина называется абсолютной шкалой температур. Она оказывается наиболее удобной при построении физических теорий.
Нет необходимости привязывать шкалу Кельвина к двум фиксированным точкам – точке плавления льда и точке кипения воды при нормальном атмосферном давлении, как это принято в шкале Цельсия.
Кроме точки нулевого давления газа, которая называется абсолютным нулем температуры, достаточно принять еще одну фиксированную опорную точку. В шкале Кельвина в качестве такой точки используется температура тройной точки воды (0,01 °С), в которой в тепловом равновесии находятся все три фазы – лед, вода и пар. По шкале Кельвина температура тройной точки принимается равной 273,16 К.
Газовые термометры громоздки и неудобны для практического применения: они используются в качестве прецизионного стандарта для калибровки других термометров.
Таким образом, давление разреженного газа в сосуде постоянного объема V изменяется прямо пропорционально его абсолютной температуре: p ~ T. С другой стороны, опыт показывает, что при неизменных объеме V и температуре T давление газа изменяется прямо пропорционально отношению количества вещества ν в данном сосуде к объему V сосуда
где N – число молекул в сосуде, NА – постоянная Авогадро, n = N / V – концентрация молекул (т. е. число молекул в единице объема сосуда). Объединяя эти соотношения пропорциональности, можно записать:
где k – некоторая универсальная для всех газов постоянная величина. Ее называют постоянной Больцмана, в честь австрийского физика Людвига Больцмана, одного из создателей молекулярно-кинетической теории. Постоянная Больцмана – одна из фундаментальных физических констант. Ее численное значение в СИ равно:
k = 1,38·10–23 Дж/К. |
Сравнивая соотношения p = nkT с основным уравнением молекулярно-кинетической теории газов, можно получить:
Средняя кинетическая энергия хаотического движения молекул газа прямо пропорциональна абсолютной температуре.
Таким образом, температура есть мера средней кинетической энергии поступательного движения молекул.
Следует обратить внимание на то, что средняя кинетическая энергия поступательного движения молекулы не зависит от ее массы. Броуновская частица, взвешенная в жидкости или газе, обладает такой же средней кинетической энергией, как и отдельная молекула, масса которой на много порядков меньше массы броуновской частицы. Этот вывод распространяется и на случай, когда в сосуде находится смесь химически невзаимодействующих газов, молекулы которых имеют разные массы. В состоянии равновесия молекулы разных газов будут иметь одинаковые средние кинетические энергии теплового движения, определяемые только температурой смеси. Давление смеси газов на стенки сосуда будет складываться из парциальных давлений каждого газа:
p = p1 + p2 + p3 + … = (n1 + n2 + n3 + …)kT. |
В этом соотношении n1, n2, n3, … – концентрации молекул различных газов в смеси. Это соотношение выражает на языке молекулярно-кинетической теории экспериментально установленный в начале XIX столетия закон Дальтона: давление в смеси химически невзаимодействующих газов равно сумме их парциальных давлений.
www.its-physics.org
Основное уравнение МКТ газов. Температура
Простейшей моделью, рассматриваемой молекулярно-кинетической теорией, является модель идеального газа. В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур. Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, объем, температура).
В результате каждого столкновения между молекулами и молекул со стенками скорости молекул могут изменяться по модулю и по направлению; на интервалах времени между последовательными столкновениями молекулы движутся равномерно и прямолинейно. В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т. е. подчиняются законам механики Ньютона.
Используя модель идеального газа, вычислим давление газа на стенку сосуда. В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υy скорости, параллельная стенке, остается неизменной (рис. 3.2.1).
|
Рисунок 3.2.1. Упругое столкновение молекулы со стенкой |
Поэтому изменение импульса молекулы будет равно 2m0υx, где m0 – масса молекулы.
Выделим на стенке некоторую площадку S (рис. 3.2.2). За время Δt с этой площадкой столкнутся все молекулы, имеющие проекцию скорости υx, направленную в сторону стенки, и находящиеся в цилиндре с основанием площади S и высотой υxΔt.
|
Рисунок 3.2.2. Определение числа столкновений молекул с площадкой S |
Пусть в единице объема сосуда содержатся n молекул; тогда число молекул в объеме цилиндра равно nSυxΔt. Но из этого числа лишь половина движется в сторону стенки, а другая половина движется в противоположном направлении и со стенкой не сталкивается. Следовательно, число ударов молекул о площадку S за время Δt равно
Поскольку каждая молекула при столкновении со стенкой изменяет свой импульс на величину 2m0υx, то полное изменение импульса всех молекул, столкнувшихся за время Δt с площадкой S, равно
По законам механики это изменение импульса всех столкнувшихся со стенкой молекул происходит под действием импульса силы FΔt, где F – некоторая средняя сила, действующая на молекулы со стороны стенки на площадке S. Но по 3-му закону Ньютона такая же по модулю сила действует со стороны молекул на площадку S. Поэтому можно записать:
Разделив обе части на SΔt, получим:
где p – давление газа на стенку сосуда.
При выводе этого соотношения предполагалось, что все n молекул, содержащихся в единице объема газа, имеют одинаковые проекции скоростей на ось X. На самом деле это не так.
В результате многочисленных соударений молекул газа между собой и со стенками в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а модули скоростей и их проекции на координатные оси подчиняются определенным закономерностям. Распределение молекул газа по модулю скоростей называется распределением Максвелла. Джеймс Максвелл в 1860 г. вывел закон распределения молекул газа по скоростям, исходя из основных положений молекулярно-кинетической теории. На рис. 3.2.3 представлены типичные кривые распределения молекул по скоростям. По оси абсцисс отложен модуль скорости, а по оси ординат – относительное число молекул, скорости которых лежат в интервале от υ до υ + Δυ. Это число равно площади выделенного на рис. 3.2.3 столбика.
|
Рисунок 3.2.3. Распределение молекул по скоростям. T2 > T1 |
Характерными параметрами распределения Максвелла являются наиболее вероятная скорость υв, соответствующая максимуму кривой распределения, и среднеквадратичная скорость
где
– среднее значение квадрата скорости.
С ростом температуры максимум кривой распределения смещается в сторону больших скоростей, при этом υв и υкв увеличиваются.
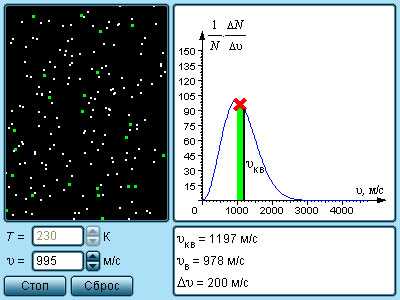 |
Модель. Распределение Максвелла. |
Чтобы уточнить формулу для давления газа на стенку сосуда, предположим, что все молекулы, содержащиеся в единице объема, разбиты на группы, содержащие n1, n2, n3 и т. д. молекул с проекциями скоростей υx1, υx2, υx3 и т. д. соответственно. При этом
Каждая группа молекул вносит свой вклад
в давление газа. В результате соударений со стенкой молекул с различными значениями проекций υxi скоростей возникает суммарное давление
Входящая в это выражение сумма – это сумма квадратов проекций υx всех n молекул в единичном объеме газа. Если эту сумму разделить на n, то мы получим среднее значение квадрата проекции скорости молекул:
Теперь формулу для давления газа можно записать в виде
Так как все направления для векторов скоростей молекул равновероятны, среднее значение квадратов их проекций на координатные оси равны между собой:
Последнее равенство вытекает из формулы:
Формула для среднего давления газа на стенку сосуда запишется в виде
Это уравнение устанавливает связь между давлением p идеального газа, массой молекулы m0, концентрацией молекул n, средним значением квадрата скорости и средней кинетической энергией поступательного движения молекул. Его называют основным уравнением молекулярно-кинетической теории газов.
Таким образом, давление газа равно двум третям средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.
В основное уравнение молекулярно-кинетической теории газов входит произведение концентрации молекул n на среднюю кинетическую энергию поступательного движения. Если предположить, что газ находится в сосуде неизменного объема V, то
(N – число молекул в сосуде). В этом случае изменение давления Δp пропорционально изменению средней кинетической энергии.
Возникают вопросы: каким образом можно на опыте изменять среднюю кинетическую энергию движения молекул в сосуде неизменного объема? Какую физическую величину нужно изменить, чтобы изменилась средняя кинетическая энергия Опыт показывает, что такой величиной является температура.
Понятие температуры тесно связано с понятием теплового равновесия. Тела, находящиеся в контакте друг с другом, могут обмениваться энергией. Энергия, передаваемая одним телом другому при тепловом контакте, называется количеством теплоты.
Тепловое равновесие – это такое состояние системы тел, находящихся в тепловом контакте, при котором не происходит теплопередачи от одного тела к другому, и все макроскопические параметры тел остаются неизменными. Температура – это физический параметр, одинаковый для всех тел, находящихся в тепловом равновесии. Возможность введения понятия температуры следует из опыта и носит название нулевого закона термодинамики.
Для измерения температуры используются физические приборы – термометры, в которых о величине температуры судят по изменению какого-либо физического параметра. Для создания термометра необходимо выбрать термометрическое вещество (например, ртуть, спирт) и термометрическую величину, характеризующую свойство вещества (например, длина ртутного или спиртового столбика). В различных конструкциях термометров используются разнообразные физические свойства вещества (например, изменение линейных размеров твердых тел или изменение электрического сопротивления проводников при нагревании).
Термометры должны быть откалиброваны. Для этого их приводят в тепловой контакт с телами, температуры которых считаются заданными. Чаще всего используют простые природные системы, в которых температура остается неизменной, несмотря на теплообмен с окружающей средой – это смесь льда и воды и смесь воды и пара при кипении при нормальном атмосферном давлении. По температурной шкале Цельсия точке плавления льда приписывается температура 0 °С, а точке кипения воды – 100 °С. Изменение длины столба жидкости в капиллярах термометра на одну сотую длины между отметками 0 °С и 100 °С принимается равным 1 °С. В ряде стран (США) широко используется шкала Фаренгейта (TF), в которой температура замерзающей воды принимается равной 32 °F, а температура кипения воды равной 212 °F. Следовательно,
Особое место в физике занимают газовые термометры (рис. 3.2.4), в которых термометрическим веществом является разреженный газ (гелий, воздух) в сосуде неизменного объема (V = const), а термометрической величиной – давление газа p. Опыт показывает, что давление газа (при V = const) растет с ростом температуры, измеренной по шкале Цельсия.
|
Рисунок 3.2.4. Газовый термометр с постоянным объемом |
Чтобы проградуировать газовый термометр постоянного объема, можно измерить давление при двух значениях температуры (например, 0 °C и 100 °C), нанести точки p0 и p100 на график, а затем провести между ними прямую линию (рис. 3.2.5). Используя полученный таким образом калибровочный график, можно определять температуры, соответствующие другим значениям давления. Экстраполируя график в область низких давлений, можно определить некоторую «гипотетическую» температуру, при которой давление газа стало бы равным нулю. Опыт показывает, что эта температура равна –273,15 °С и не зависит от свойств газа. На опыте получить путем охлаждения газ в состоянии с нулевым давлением невозможно, так как при очень низких температурах все газы переходят в жидкое или твердое состояние.
|
Рисунок 3.2.5. Зависимость давления газа от температуры при V = const |
Английский физик У. Кельвин (Томсон) в 1848 г. предложил использовать точку нулевого давления газа для построения новой температурной шкалы (шкала Кельвина). В этой шкале единица измерения температуры такая же, как и в шкале Цельсия, но нулевая точка сдвинута:
В системе СИ принято единицу измерения температуры по шкале Кельвина называть кельвином и обозначать буквой K. Например, комнатная температура TС = 20 °С по шкале Кельвина равна TК = 293,15 К.
Температурная шкала Кельвина называется абсолютной шкалой температур. Она оказывается наиболее удобной при построении физических теорий.
Нет необходимости привязывать шкалу Кельвина к двум фиксированным точкам – точке плавления льда и точке кипения воды при нормальном атмосферном давлении, как это принято в шкале Цельсия.
Кроме точки нулевого давления газа, которая называется абсолютным нулем температуры, достаточно принять еще одну фиксированную опорную точку. В шкале Кельвина в качестве такой точки используется температура тройной точки воды (0,01 °С), в которой в тепловом равновесии находятся все три фазы – лед, вода и пар. По шкале Кельвина температура тройной точки принимается равной 273,16 К.
Газовые термометры громоздки и неудобны для практического применения: они используются в качестве прецизионного стандарта для калибровки других термометров.
Таким образом, давление разреженного газа в сосуде постоянного объема V изменяется прямо пропорционально его абсолютной температуре: p ~ T. С другой стороны, опыт показывает, что при неизменных объеме V и температуре T давление газа изменяется прямо пропорционально отношению количества вещества ν в данном сосуде к объему V сосуда
где N – число молекул в сосуде, NА – постоянная Авогадро, n = N / V – концентрация молекул (т. е. число молекул в единице объема сосуда). Объединяя эти соотношения пропорциональности, можно записать:
где k – некоторая универсальная для всех газов постоянная величина. Ее называют постоянной Больцмана, в честь австрийского физика Людвига Больцмана, одного из создателей молекулярно-кинетической теории. Постоянная Больцмана – одна из фундаментальных физических констант. Ее численное значение в СИ равно:
k = 1,38·10–23 Дж/К. |
Сравнивая соотношения p = nkT с основным уравнением молекулярно-кинетической теории газов, можно получить:
Средняя кинетическая энергия хаотического движения молекул газа прямо пропорциональна абсолютной температуре.
Таким образом, температура есть мера средней кинетической энергии поступательного движения молекул.
Следует обратить внимание на то, что средняя кинетическая энергия поступательного движения молекулы не зависит от ее массы. Броуновская частица, взвешенная в жидкости или газе, обладает такой же средней кинетической энергией, как и отдельная молекула, масса которой на много порядков меньше массы броуновской частицы. Этот вывод распространяется и на случай, когда в сосуде находится смесь химически невзаимодействующих газов, молекулы которых имеют разные массы. В состоянии равновесия молекулы разных газов будут иметь одинаковые средние кинетические энергии теплового движения, определяемые только температурой смеси. Давление смеси газов на стенки сосуда будет складываться из парциальных давлений каждого газа:
p = p1 + p2 + p3 + … = (n1 + n2 + n3 + …)kT. |
В этом соотношении n1, n2, n3, … – концентрации молекул различных газов в смеси. Это соотношение выражает на языке молекулярно-кинетической теории экспериментально установленный в начале XIX столетия закон Дальтона: давление в смеси химически невзаимодействующих газов равно сумме их парциальных давлений.
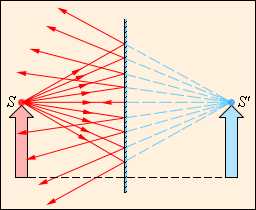
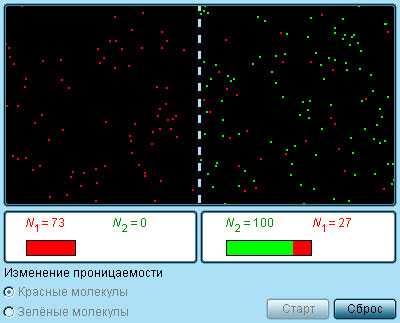 |
Модель. Полупроницаемая мембрана. |
questions-physics.ru
2.1.2 Идеальный газ. Давление и температура газа. Шкала температур
В молекулярно-кинетической теории пользуются идеализированной моделью идеального газа, согласно которой:
1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;
2) между молекулами газа отсутствуют силы взаимодействия;
3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие. Модель идеального газа можно использовать при изучении реальных газов, так как они в нормальных условиях, близки по своим свойствам требованиям, предъявляемым моделью идеального газа.
Действительно, совершая беспорядочные движения, молекулы газа время от времени приближаются к стенкам сосуда или к поверхности других тел на достаточно малые расстояния. Точно так же молекулы могут подойти друг к другу достаточно близко и между молекулами газа или между молекулой газа и молекулами вещества стенки возникают силы взаимодействия, которые очень быстро убывают с расстоянием. Под действием этих сил молекулы газа изменяют направление своего движения. Этот процесс (изменения направления), как известно, называется столкновением.
Столкновения молекул между собой играют очень большую роль в состоянии газа. И мы их позже детально изучим. Сейчас важно учесть столкновения молекул со стенками сосуда или с любой другой поверхностью, соприкасающейся с газом. Именно взаимодействием молекул газа и стенок определяется сила, испытываемая стенками со стороны газа, которую принято характеризовать давлением р, т. е. силой F, отнесенной к единице площади S поверхности стенки, нормальной к этой стенке:
Свойство газа оказывать давление на стенки содержащего его сосуда — одно из основных свойств газа. Именно своим давлением газ чаще всего и обнаруживает свое присутствие. Поэтому величина давления является одной из главных характеристик газа.
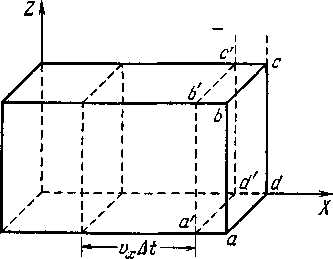
Допустим, что газ заключен в сосуд, имеющий форму параллелепипеда (рисунок – 2.4), и что газ находится в состоянии равновесия. Вычислим давление газа на одну из стенок сосуда, например на правую боковую стенку abed. Направим координатную ось X вдоль ребра параллелепипеда перпендикулярно к стенке abed, как это показано на рисунке – 2.4). Как бы ни были направлены скорости v молекул, нас будут интересовать только проекции vx скоростей молекул на ось X: по направлению к стенке abed молекулы движутся именно со скоростью vx.
|
Рисунок – 2.4 |
Выделим мысленно слой газа толщиной Δх, прилегающий к выбранной стенке. На него со стороны деформированной стенки действует упругая сила F. С такой же по абсолютному значению силой и газ действует на стенку. По второму закону Ньютона импульс силы F∆t (где ∆t — некоторый произвольный промежуток времени) равен изменению импульса газа в нашем слое. Но газ находится в состоянии равновесия, так что слой никакого приращения импульса в направлении импульса силы (против положительного направления оси X) не получает. Происходит это потому, что из-за молекулярных движений выделенный слой получает импульс противоположного направления и, конечно, такой же по абсолютному значению. Его нетрудно вычислить.
При беспорядочных движениях газовых молекул за время ∆t в наш слой слева направо входит некоторое число молекул и столько же молекул выходят из него в обратном направлении — справа налево. Входящие молекулы несут с собой определенный импульс. Выходящие из выделенного объема, молекулы несут такой же импульс противоположного знака, так что общий импульс, получаемый слоем, равен алгебраической сумме импульсов входящих в слой и выходящих из него молекул. Найдем число молекул, входящих в наш слой слева за время ∆t.
За это время к границе a‘b‘c‘d‘ слева могут подойти те молекулы, которые находятся от нее на расстоянии, не превышающем vx ∆t. Все они находятся в объеме параллелепипеда с площадью основания S (это площадь рассматриваемой стенки) и длиной vx ∆t, т. е. в объеме Svx ∆t. Если в единице объема сосуда содержится п молекул, то в указанном объеме находится nSvx ∆t молекул. Но из них лишь половина движется слева направо и попадает в слой. Другая половина движется от него и в слой не попадает. Следовательно, за время ∆t в слой слева направо входит 1/2nSv∆t молекул. Каждая из них обладает импульсом mvx, и общий импульс, вносимый ими в слой, равен 1/2nmvx2S ∆t. За это же время слой покидает, двигаясь справа налево, такое же число молекул с таким жеобщим импульсом, но обратного знака. Таким образом, из-за прихода в слой молекул с положительным импульсом и ухода из него молекул с отрицательным импульсом общее изменение импульса слоя равно 1/2nmvx2S ∆t – (-1/2nmvx2S ∆t) = nmvx2S ∆t. Это-то изменение импульса слоя и компенсирует то изменение, которое должно было бы произойти под действием импульса силы F At. Поэтому мы можем написать: F ∆t = nmvx2S ∆t. Разделив обе части этого равенства на S ∆t, получаем: p = F/S = nmvx2. До сих пор мы молча предполагали, что у всех молекул газа одинаковые проекции скорости vx. В действительности это, конечно, не так. И скорости молекул v, и их проекции vx на ось X у разных молекул, разумеется, различны. Учтем различие скоростей молекул и их проекций на оси координат тем, что заменим величину vx2, входящую в последнюю формулу, ее средним значением ‹vx2›, так что формуле для давления газа мы придадим вид: p =nm‹vx2›. Для скорости v каждой молекулы можно написать: v2 = vx2+-v2y+vz2:
‹vx2› = ‹vx2›+‹v2y›+‹vz2›. |
Из-за полной беспорядочности молекулярных движений можно полагать, что средние значения квадратов проекций скоростей на три оси координат равны друг другу, т. е., ‹vx2›=v2y›=‹vz2›. А это значит, что ‹vx2›= v2/3. Подставив это выражение в формулу Вычислим давление газа на одну из стенок давления получаем: р = mv2/3, или, умножив и разделив правую часть этого равенства на двойку, найдем
Приведенные простые рассуждения справедливы для любой стенки сосуда и для любой площадки, которую мысленно можно поместить в газ. Во всех случаях мы получим для давления газа результат, выраженный последней формулой. Величина mv2/2 в ней представляет собой среднюю кинетическую энергию одной молекулы газа. Следовательно, давление газа равно двум третям средней кинетической энергии молекул, содержащихся в единице объема газа. Это – один из важнейших выводов кинетической теории идеального газа. Он устанавливает связь между молекулярными величинами, т. е. величинами, относящимися к отдельной молекуле, и макроскопической характеристикой газа – величиной давления, характеризующей газ как целое, — величиной, непосредственно измеряемой на опыте. Уравнение (2.9) называют основным уравнением кинетической теории идеальных газов. Важно подчеркнуть, что давление газа определяется средней кинетической энергией его молекул. Это значит, что давление газа — величина, связанная с тем, что газ состоит из большого числа молекул.
Одним из важных термодинамических параметров, характеризующих состояние газа, является температура. Температура играет важную роль не только в термодинамике, но и в физике в целом. Если тело или система тел не находится в состоянии теплового равновесия и если система изолирована (не взаимодействует с другими телами), то через некоторое время состояние теплового равновесия устанавливается само собой. Состояние теплового равновесия — это и есть состояние, в которое переходит любая изолированная система.
Одним из признаков состояния теплового равновесия и является равенство температур всех частей тела или всех тел системы. Известно, что в процессе установления теплового равновесия, т.е. при выравнивании температуры двух тел, происходит передача теплоты от одного тела другому. Следовательно, с экспериментальной точки зрения, температура тела — это величина, которая определяет, будет ли оно другому телу с иной температурой передавать теплоту или получать от него теплоту.
Этот простой опыт показывает, что температура — это величина, характеризующая состояние теплового равновесия: у тел, находящихся в состоянии теплового равновесия, температуры одинаковы. И наоборот, тела с одинаковой температурой находятся в тепловом равновесии друг с другом. А если два тела находятся в тепловом равновесии с каким-нибудь третьим телом, то оба тела находятся в тепловом равновесии и между собой. Это важное утверждение является одним из основных законов природы. Температура — физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.
Для измерения температуры издавна пользуются тем, что при изменении температуры тела изменяются, и его свойства. Изменяются, следовательно, величины, характеризующие эти свойства. Поэтому, для создания термометра, выбирают какое-либо вещество (термометрическое вещество) и определенную величину, характеризующую свойство вещества (термометрическую величину). Выбор того и другого совершенно произволен. В бытовых термометрах, например, термометрическим веществом является ртуть, а термометрической величиной — длина ртутного столбика.
Для того чтобы величине температуры можно было сопоставить определенные числовые значения, нужно еще задаться той или иной зависимостью термометрической величины от температуры. Выбор этой зависимости тоже произволен: ведь пока нет термометра, нельзя опытным путем установить эту зависимость. В случае ртутного термометра, например, избирается линейная зависимость длины ртутного столбика (объема ртути) от температуры.
Остается еще установить единицу температуры — градус (хотя в принципе ее можно было бы выражать в тех же единицах, в которых измеряется термометрическая величина, например по ртутному термометру — в сантиметрах). Величина градуса избирается тоже произвольно (как и термометрическое вещество, так и вид функции, связывающей термометрическую величину с температурой).
Размер градуса устанавливается следующим образом. Выбирают, опять-таки произвольно, две температуры (их называют реперными точками) — обычно это температуры таяния льда и кипения воды при атмосферном давлении — и делят этот температурный интервал на некоторое (тоже произвольное) число равных частей — градусов, а одной из этих двух температур приписывают определенное числовое значение. Тем самым определяется значение второй температуры и любой промежуточной. Таким образом, получают температурную шкалу.
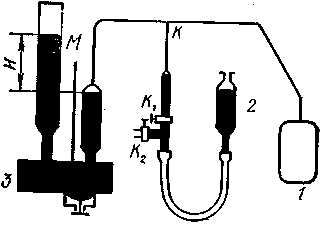
Современная термометрия основана на шкале идеального газа, устанавливаемой с помощью газового термометра. В принципе газовый термометр — это закрытый сосуд, наполненный идеальным газом и снабженный манометром для измерения давления газа. Термометрическим веществом в таком термометре служит идеальный газ, а термометрической величиной — давление газа при постоянном объеме. Измерение температуры производится косвенно по изменению давления газа в сосуде 1 при постоянном объеме Это позволяет принять, что отношение давлений при температурах кипения воды (рк) и таяния льда (р0) равно отношению самих этих температур: рк/ р0 = Тк/ Т0
Отношение рк/р0 легко определить из опыта. Многочисленные измерения показали, что рк/ р0 = 1,3661. Таково, следовательно, и значение отношения температур: Тк/Т0 = 1,3661. Размер градуса выбирается делением разности Тк — Т0 на сто частей: Тк – Т0 =100.
Из последних двух равенств следует, что температура таяния льда Т0 по выбранной нами шкале равна 273,15 градусов, а температура кипения воды Тк равна 373,15 градусов. Для того чтобы при помощи газового термометра измерить температуру какого-нибудь тела, надо привести тело в контакт с газовым термометром и, дождавшись равновесия, измерить давление р газа в термометре. Тогда температура тела Т определяется по формуле
Т = 273,15(р/р0) | (2.10), |
где р0 —- давление газа в термометре, помещенном в тающий лед. Так можно получить термометрическую шкалу эмпирическим методом – эмпирическую шкалу температур. В практике газовым термометром пользуются крайне редко. На него возложена более ответственная роль — по нему градуируются все употребляемые термометры. Таким можно получить бесчисленное множество различных термометров и температурных шкал.
Создание хороших термометров и измерение температуры, особенно в широком диапазоне ее изменения,— задачи не простые. Измерить температуру какого-нибудь тела — значит сравнить ее с температурой эталона. Естественно за эталон выбрать идеальный газ, так как температура такого газа легко определяется через макропараметры, такие, как объем или давление. Причем если одна из этих величин фиксируется, то другая для данной массы газа изменяется линейно с изменением температуры Т. Чтобы температуры двух тел, исследуемого и эталонного, стали равными, необходимо привести их в тепловое равновесие.
Газовые термометры используются обычно как первичные приборы, по которым градуируют вторичные термометры, применяемые непосредственно в экспериментах. Из вторичных термометров наибольшее распространение получили жидкостные термометры, термометры сопротивления и термоэлементы.
Простейшими термометрами являются жидкостные термометры, где термометрическим телом, является ртуть или этиловый спирт. Ртутный термометр представляет собой сферический или цилиндрический стеклянный резервуар, к которому припаян тонкий капилляр из стекла того же сорта. Отсчет температуры производят по шкале, прикрепленной к капилляру (рисунок – 2.5). Обычно жидкостные термометры применяются в диапазоне температур от 125 до 900 К. Нижняя граница измеряемой температуры определяется свойствами жидкости, верхняя — свойствами стекла капилляра.
На рисунке – 2.6 изображен ртутный термометр, состоящий из небольшого резервуара с ртутью, оканчивающегося тонким капилляром. При нагревании ртуть расширяется, и ее уровень h в капилляре поднимается. Шкала и начало отсчета температуры могут быть выбраны произвольно.
| |
Рисунок – 2.5 | Рисунок – 2.6 |
Наиболее распространенной в международной практике шкалой для измерения температуры является стоградусная шкала Цельсия. В этом случае за нуль температурной шкалы (0° С) принята температура плавления льда при нормальных условиях, т. е. при давлении р = 1 атм, а за 100°— температура кипения воды (при тех же условиях). Разделив тогда высоту капилляра h100 между этими двумя точками на 100 равных частей, можно определить температуру t в градусах Цельсия по отношению высоты поднятия ртути в капилляре ht к интервалу между двумя постоянными точками, т. е.
t = (h1/h100)*100°С | (2.11). |
Такое определение температуры пригодно лишь для грубых измерений в быту. При более точных измерениях. обнаруживается, что для разных термометрических жидкостей, например для ртутного и спиртового термометров, при одинаковой температуре численные значения отношений h1/h100– совпадают друг с другом лишь для выбранных постоянных точек. При промежуточных же температурах показания обоих термометров будут несколько расходиться, так как законы расширения различных жидкостей и сосудов, их содержащих различны.
В современной технике наиболее удобными являются электрические методы измерения температуры. В так называемых термометрах сопротивления используется изменение сопротивления металлов и полупроводников при их нагревании. Термоэлементами или термопарами измеряется электродвижущая сила, возникающая при нагревании места контакта двух металлов или полупроводников.
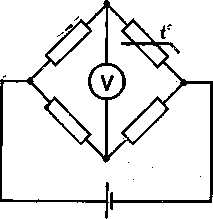
В термометрах сопротивления термометрическим телом является металл или полупроводник, сопротивление которого изменяется с температурой. Изменение сопротивления с температурой измеряют при помощи мостовых схем (рисунок – 2.7). Термометры сопротивления из металлов применяются в интервале температур от 70 до 1300 К, из полупроводников (термисторы) — в интервале от 150 до 400 К, а углеродистые — до температур жидкого гелия.
При любом методе определения температуры на температурной шкале можно отметить некоторую точку, имеющую абсолютное значение. Эта точка отвечает температуре, при которой отсутствует хаотическое (тепловое) движение молекул, и носит название абсолютного нуля температуры (Т = 0°С = 0°К). В случае идеального газа значению Т = 0 отвечает отсутствие кинетической энергии поступательного движения молекул и отсутствие давления. Такая шкала для измерения температуры называется абсолютной шкалой, единицей измерения служит градус Кельвина (К). Не следует думать, что при абсолютном нуле температуры прекращается всякое движение частиц вещества. Даже если все молекулы газа остановятся, то внутри них будут двигаться электроны по определенным орбитам вокруг ядер, определенным образом будут участвовать в движении протоны и нейтроны внутри ядер. Ниже мы убедимся, что, например, средняя кинетическая энергия свободных электронов в металле при абсолютном нуле в сотни раз превышает среднюю кинетическую энергию молекул газа при комнатной температуре и т. д.
|
Рисунок – 2.7 |
Абсолютный нуль температуры означает не отсутствие движения, но такое состояние тела, при котором дальнейшее уменьшение интенсивности этого движения за счет отдачи его энергии окружающим телам невозможно.
Следовательно, при абсолютном нуле система находится в состоянии с наименьшей возможной энергией. Показания шкалы Цельсия и абсолютной шкалы связаны между собой следующим образом:
studfiles.net
Связь между давлением, температурой, объемом и количеством молей газа (“массой” газа). Универсальная (молярная) газовая постоянная R. Уравнение Клайперона-Менделеева = уравнение состояния идеального газа.
Связь между давлением, температурой, объемом и количеством молей газа (“массой” газа). Универсальная (молярная) газовая постоянная R. Уравнение Клайперона-Менделеева = уравнение состояния идеального газа.
|
Ограничения практической применимости: Внутри диапазона точность уравнения превосходит точность обычных современных инженерных средств измерения. Для инженера важно понимать, что для всех газов возможна существенная диссоциация или разложение при повышении температуры. |
|
|
где:
|
|
Давайте решим парочку задач относительно газовых объемных и массовых расходов в предположении, что состав газа не изменяется (газ не диссоциирует) – что верно для большинства газов в указанных выше пределах применимости.
1) Доставка объемов газа одинаковой массы при одинаковом давлении но различных температурах.
Данная задача актуальна в основном, но не только, для применений и устройств, в которых напрямую измеряется объем газа.
Пусть счетчик (расходомер) в точке доставки дает объемные накопленные расходы V1 и V2, при температурах, соответственно, T1 и T2 и, пусть T1< T2 . Тогда мы знаем, что:
Естественно, V1< V2 для одинаковых количеств газа при данных условиях. Попробуем сформулировать несколько важных на практике выводов для данного случая:
- показатели объемного счетчика газа тем “весомее”, чем ниже температура
- выгодно поставлять “теплый” газ
- выгодно покупать “холодный” газ
Как с этим бороться? Необходима хотя бы простая температурная компенсация, т.е в считающее устройство должна подаваться информация с дополнительного датчика температуры.
2) Доставка объемов газа одинаковой массы при одинаковой температуре, но различных давлениях.
Данная задача актуальна в основном, но не только, для применений и устройств, в которых напрямую измеряется скорость газа.
Пусть счетчик (расходомер) в точке доставки дает объемные накопленные расходы V1 и V2, при давлениях, соответственно, P1 и P2 и, пусть P1< P2 . Тогда мы знаем, что:
Естественно, V1>V2 для одинаковых количеств газа при данных условиях. Попробуем сформулировать несколько важных на практике выводов для данного случая:
- показатели объемного счетчика газа тем “весомее”, чем выше давление
- выгодно поставлять газ низкого давления
- выгодно покупать газ высокого давления
Как с этим бороться? Необходима хотя бы простая компенсация по давлению, т.е в считающее устройство должна подаваться информация с дополнительного датчика давления.
В заключение, хотелось бы отметить, что, теоретически, каждый газовый счетчик должен иметь и температурную компенсацию и компенсацию по давлению. Практически же….. привет от проекта TehTab.ru.tehtab.ru
АБСОЛЮТНАЯ ТЕМПЕРАТУРА ГАЗА: Смотреть что такое “АБСОЛЮТНАЯ ТЕМПЕРАТУРА” в других словарях:
 Средняя кинетическая энергия поступательного движения молекул прямо пропорциональна абсолютной температуре. Есть и абсолютная шкала температур. 2. Какие преимущества имеет абсолютная шкала температур по сравнению со шкалой Цельсия?
Средняя кинетическая энергия поступательного движения молекул прямо пропорциональна абсолютной температуре. Есть и абсолютная шкала температур. 2. Какие преимущества имеет абсолютная шкала температур по сравнению со шкалой Цельсия?
Сейчас вы узнаете об этом, а также о том, какова точная связь между температурой и средней кинетической энергией молекул. Вместо температуры , выражаемой в энергетических единицах, введем температуру, выражаемую в привычных для нас градусах.
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
По этой формуле вводится температурная шкала (в градусах), не зависящая от вещества, используемого для измерения температуры.Абсолютный нуль температуры. Температура, определяемая формулой (9.6), очевидно, не может быть отрицательной, так как все величины, стоящие в левой части этой формулы, заведомо положительны.
Определим коэффициент k в формуле (9.6) так, чтобы один кельвин (1 К) был равен градусу по шкале Цельсия (1°С). Мы знаем значения величины при 0°С и 100°С (см. формулы (9.2) и (9.4)). Это одна из наиболее важных постоянных в молекулярно-кинетической теории.Связь абсолютной шкалы и шкалы Цельсия. Зная постоянную Больцмана, можно найти значение абсолютного нуля по шкале Цельсия. Для этого найдем сначала значение абсолютной температуры, соответствующее 0°С. Так как при 0°С , то . Один кельвин и один градус шкалы Цельсия совпадают.
Докажем это. Левые части уравнений и одинаковы. 1. Гелий, после водорода, в наименьшей степени отклоняется от законов идеального газа (для воздуха, азота, углекислого газа и т. п. эти отклонения больше, чем для гелия). Исключение водорода связано с тем, что при высоких температурах он начинает химически действовать на материал сосуда (как правило, стекло), в котором он находится. В этих условиях гелий заменяют на азот. При низких температурах становятся заметными отступления от простого закона (2.3.1).

Поэтому вид функциональной зависимости между температурой и термометрической величиной первоначально можно выбрать только произвольно. Таким образом, в идеально-газовой шкале температур в качестве термометрического тела выбирают газообразный гелий (азот), а термометрической величиной – его давление при постоянном объеме. А. т. обозначается символом Т, выражается в Кельвинах (К) и отсчитывается от абсолютного нуля температуры.
Абсолютная температура — Хаотическое тепловое движение на плоскости частиц газа таких как атомы и молекулы Существует два определения температуры. В зимнее же время года, когда температура всасываемого газа ниже температуры охлаждающей воды, оно еще значительнее. Аналогично вакуумный кран срабатывает в случаях, когда давление внутри емкости становится ниже атмосферного или понижается температура.
Чем выше температура, тем быстрее движутся молекулы
Термодинамическая температура обозначается буквой T{\displaystyle T}, измеряется в Кельвинах(K){\displaystyle (K)} и отсчитывается по абсолютной термодинамической шкале (Кельвина).
Измерение температуры прошло долгий и трудный путь в своём развитии. Так как температура не может быть измерена непосредственно, то для её измерения использовали свойства термометрических тел, которые находились в функциональной зависимости от температуры.
Это самая низкая температура в природе, та «наибольшая или последняя степень холода», существование которой предсказывал Ломоносов.Абсолютная шкала температур
Отсутствие непрерывности эмпирических шкал связано с отсутствием в природе вещества, которое способно сохранять свои свойства во всём диапазоне возможных температур. В 1848 г. Томсон (лорд Кельвин) предложил выбрать градус температурной шкалы таким образом, чтобы в её пределах эффективность идеальной тепловой машины была одинаковой. Это соотношение может быть использовано для построения абсолютной термодинамической температуры.

Преимущество этой шкалы состоит в том, что давление идеального газа при V=const{\displaystyle V=const} изменяется линейно с температурой. Поскольку даже сильно разреженные газы по своим свойствам несколько отличаются от идеального газа, то реализация идеально — газовой шкалы связана с определёнными трудностями.
Следует, однако, оговориться: несмотря на то, что численно термодинамическая и идеально-газовая шкалы абсолютно идентичны, с качественной точки зрения между ними есть принципиальная разница. Только термодинамическая шкала является абсолютно независимой от свойств термометрического вещества. 4.Как уже было указано, точное воспроизведение термодинамической шкалы, а также идеально-газовой, сопряжено с серьёзными трудностями.
Воспроизедение термодинамической (идеально-газовой) температурной шкалы в диапазоне от 10 до 1337 K{\displaystyle K} возможно с помощью газового термометра. Однако точное определение температуры требует, чтобы температура измерялась объективно, с помощью приборов. Такие приборы называются термометрами и измеряют так называемую эмпирическую температуру. В термодинамике температура — это интенсивная термодинамическая величина.
В молекулярно-кинетической теории показывается, что температура пропорциональна средней кинетической энергии частиц системы. Для системы, находящейся в термодинамическом равновесии, все эти параметры равны друг другу, и их называют просто температурой системы.
Среду с одинаковыми во всех точках значениями температуры называют термически однородной. Если в системе два тела имеют одинаковую температуру, то между ними не происходит передачи кинетической энергии частиц (тепла). Если же существует разница температур, то тепло переходит от тела с более высокой температурой к телу с более низкой. Свойства температуры изучает раздел физики — термодинамика.
Второе уравнение для определения значений температур в реперных точках абсолютной шкалы находится измерением давлений P1 и P2 соответствующих температурам Т1 и Т2 в реперных точках. Английский ученый У. Кельвин (1824-1907) ввел абсолютную шкалу температур.
Предлагаю также ознакомиться:
kakbypridaser.ru